【学习笔记】[ABC274Ex] XOR Sum of Arrays
有点难😅
真的是 A B C ABC ABC的难度吗😅
非常精妙的哈希题目。
定义矩阵乘法: c i , j = ⊕ ( a i , k & b k , j ) c_{i,j}=\oplus (a_{i,k}\& b_{k,j}) ci,j=⊕(ai,k&bk,j)
之所以可以矩阵乘法是因为满足 ( a ⊕ b ) & c = ( a & c ) ⊕ ( b & c ) (a\oplus b)\& c=(a\& c)\oplus (b\& c) (a⊕b)&c=(a&c)⊕(b&c)
其实非常好验证,就把两个运算符按顺序写下来,然后把括号拆开,看等式两边是否恒等即可。
定义对于序列 { a i } \{a_i\} {ai}的哈希规则为,将每个 a k a_k ak与上 k − 1 k-1 k−1个 p p p后的结果全部异或起来
因为 ( a ⊕ b ) & p = ( a & p ) ⊕ ( b & p ) (a\oplus b)\&p=(a\& p)\oplus (b\& p) (a⊕b)&p=(a&p)⊕(b&p),所以如果 c i = a i ⊕ b i c_i=a_i\oplus b_i ci=ai⊕bi,那么 { c i } \{c_i\} {ci}的哈希值就是把 { a i } \{a_i\} {ai}和 { b i } \{b_i\} {bi}对应的哈希值异或起来
但是发现与上的 p p p都是相同的,所以这个方案冲突的概率很大
仔细观察正解的代码,发现他是把 p p p设计成了一个 M × M M\times M M×M的 01 01 01矩阵 (其中 M M M表示二进制位数,也就是 64 64 64), a i a_i ai看成一个长度为 M M M的 01 01 01向量 ,这个向量的第 i i i位就是 a i a_i ai在二进制下的第 i i i位
不妨形式化的写一下,首先我们随机一个矩阵 p p p,哈希值就是 ⊕ i = 1 n v i p i − 1 \oplus_{i=1}^nv_ip^{i-1} ⊕i=1nvipi−1。发现 c i = a i ⊕ b i c_{i}=a_{i}\oplus b_{i} ci=ai⊕bi那不就是把两个向量做按位异或吗。
直接倍增的复杂度是 O ( n M 3 log n ) O(nM^3\log n) O(nM3logn),考虑优化。
注意到是 01 01 01矩阵,所以可以把同一行压成一个 64 64 64位整数,这样转移优化到了 O ( M 2 ) O(M^2) O(M2)。
最终复杂度 O ( n M 2 log n ) O(nM^2\log n) O(nM2logn)。瓶颈在于倍增预处理,不知道可不可以做的更好。
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define ull unsigned long long
using namespace std;
const int N=5e5+5;
const int M=64;
mt19937_64 t(time(0));
struct Matrix{ull c[M];Matrix(){memset(c,0,sizeof c);}Matrix operator *(const Matrix &a)const{Matrix r;for(int i=0;i<M;i++){for(int j=0;j<M;j++){if(c[i]>>j&1){r.c[i]^=a.c[j];}}}return r;}
}pw[20];
int n,m;
ll a[N];
ull st[N][20];
ull get(ull x,Matrix y){ull res(0);for(int i=0;i<M;i++){if(x>>i&1)res^=y.c[i];}return res;
}
void write(ull x){if(x<10){cout<<(char)('0'+x);return;}write(x/10),cout<<(char)('0'+x%10);
}
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n>>m;srand(time(0));for(int i=1;i<=n;i++)cin>>a[i],st[i][0]=a[i];for(int i=0;i<M;i++){pw[0].c[i]=t();}for(int i=1;i<20;i++)pw[i]=pw[i-1]*pw[i-1];for(int j=1;j<20;j++){for(int i=1;i<=n-(1<<j)+1;i++){st[i][j]=st[i][j-1]^get(st[i+(1<<j-1)][j-1],pw[j-1]);}}for(int i=1;i<=m;i++){int b,c,d,e,f,g;cin>>b>>c>>d>>e>>f>>g;for(int j=19;j>=0;j--){if(b+(1<<j)-1<=c&&f+(1<<j)-1<=g&&(st[b][j]^st[d][j])==st[f][j]){b+=(1<<j),d+=(1<<j),f+=(1<<j);}}if(b>c){if(f>g)cout<<"No"<<"\n";else cout<<"Yes"<<"\n";}else{if(f>g)cout<<"No"<<"\n";else if((a[b]^a[d])<a[f])cout<<"Yes"<<"\n";else cout<<"No"<<"\n";}}
}
相关文章:

【学习笔记】[ABC274Ex] XOR Sum of Arrays
有点难😅 真的是 A B C ABC ABC的难度吗😅 非常精妙的哈希题目。 定义矩阵乘法: c i , j ⊕ ( a i , k & b k , j ) c_{i,j}\oplus (a_{i,k}\& b_{k,j}) ci,j⊕(ai,k&bk,j) 之所以可以矩阵乘法是因为满足 ( a ⊕ b )…...
抖音web频道爬虫
抖音web频道爬虫代码: <?php header(Content-Type:application/json; charsetutf-8);//抖音频道爬虫class DouyinChannel{private $app_id 1;private $spider_code 1;private $channels [["channel_name" > "热点","url"…...
总结)
sql中的替换函数replace()总结
1,表达式 --replace()--语法: REPLACE ( string_expression , string_pattern , string_replacement )--参数:string_expression:字符串表达式string_pattern:想要查找的子字符串string_replacement&#…...
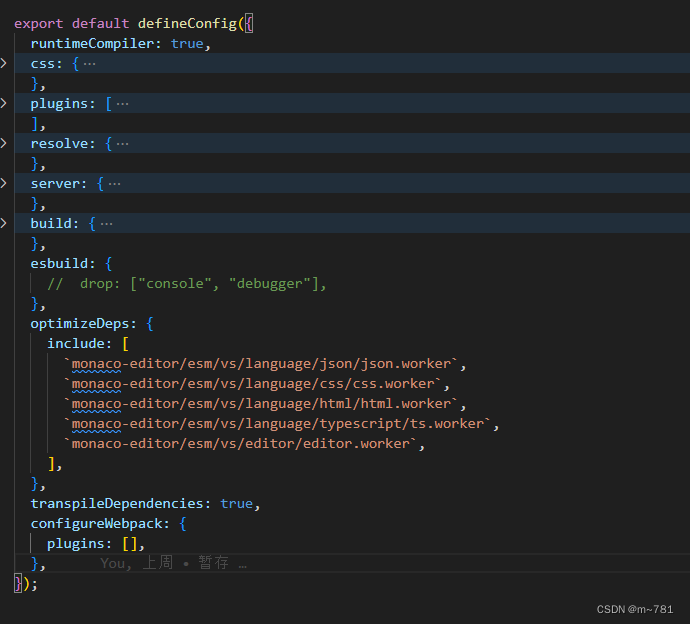
vue3 vite使用 monaco-editor 报错
报错:Unexpected usage at EditorSimpleWorker.loadForeignModule 修改配置: "monaco-editor-webpack-plugin": "^4.2.0",删除不用 版本: "monaco-editor": "^0.28.1", 修改如下: opti…...

微信小程序获取蓝牙权限
要获取微信小程序中的蓝牙权限,您可以按照以下步骤进行操作: 1. 在 app.json 文件中添加以下代码: "permissions": { "scope.userLocation": { "desc": "需要获取您的地理位置授权以搜索…...

GE 8920-PS-DC安全模块
安全控制: 这个安全模块通常用于实现工业自动化系统中的安全控制功能。它可以监测各种安全参数,如机器运动、温度、压力等,以确保系统在安全范围内运行。 PLC兼容性: 通常,这种安全模块可以与可编程逻辑控制器&#x…...
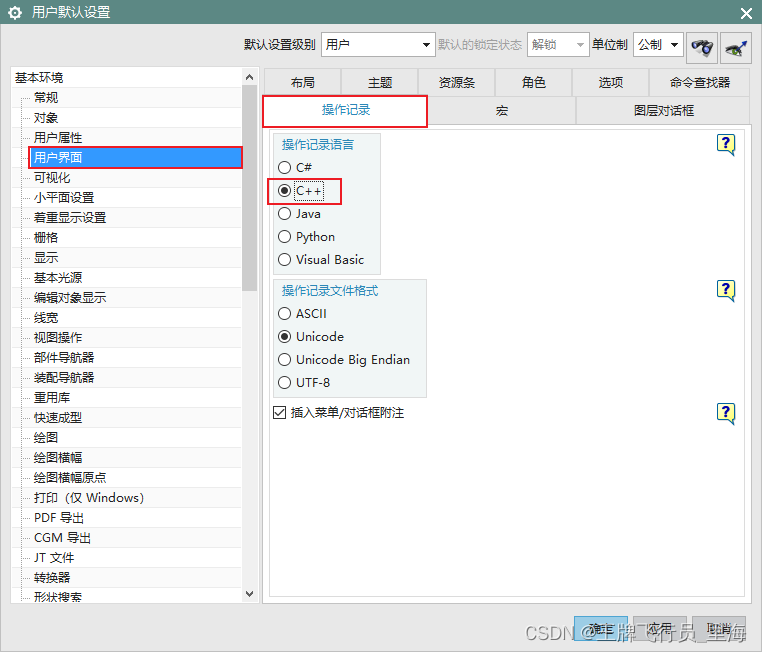
UG\NX二次开发 使用BlockUI设计对话框时,如何设置默认的开发语言?
文章作者:里海 来源网站:王牌飞行员_里海_里海NX二次开发3000例,C\C++,Qt-CSDN博客 简介: NX二次开发使用BlockUI设计对话框时,如何设置默认的代码语言? 效果: 方法: 依次打开“文件”->“实用工具”->“用户默认设置”->“用户界面”->“操作记录”->“…...
W5500-EVB-PICO进行UDP组播数据回环测试(九)
前言 上一章我们用我们的开发板作为UDP客户端连接服务器进行数据回环测试,那么本章我们进行UDP组播数据回环测试。 什么是UDP组播? 组播是主机间一对多的通讯模式, 组播是一种允许一个或多个组播源发送同一报文到多个接收者的技术。组播源将…...
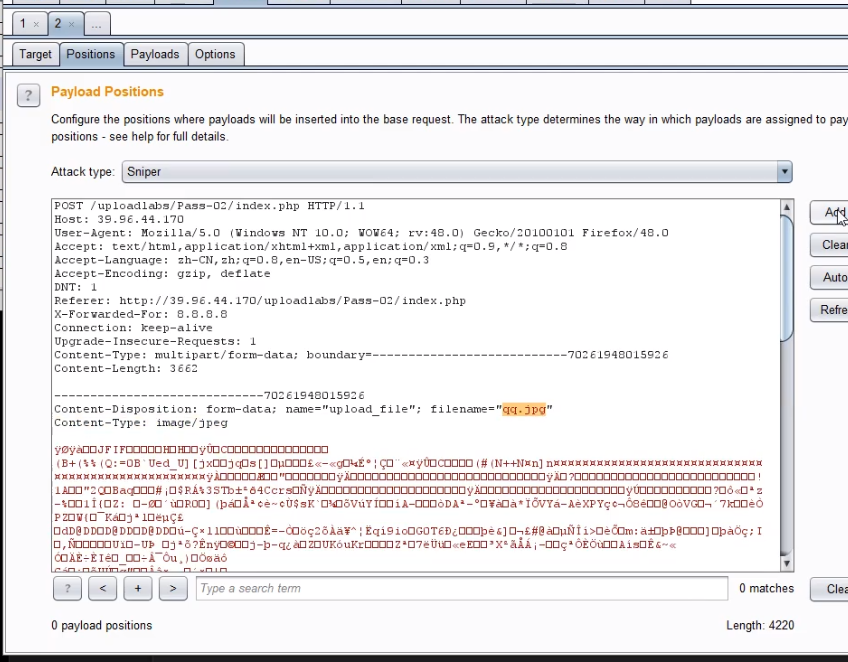
24 WEB漏洞-文件上传之WAF绕过及安全修复
目录 WAF绕过上传参数名解析:明确哪些东西能修改?常见绕过方法:符号变异-防匹配( " ;)数据截断-防匹配(%00 ; 换行)重复数据-防匹配(参数多次)搜索引擎搜索fuzz web字典文件上传安全修复方案 WAF绕过 safedog BT(宝塔) XXX云盾 宝塔过滤的比安全狗厉害一些&a…...
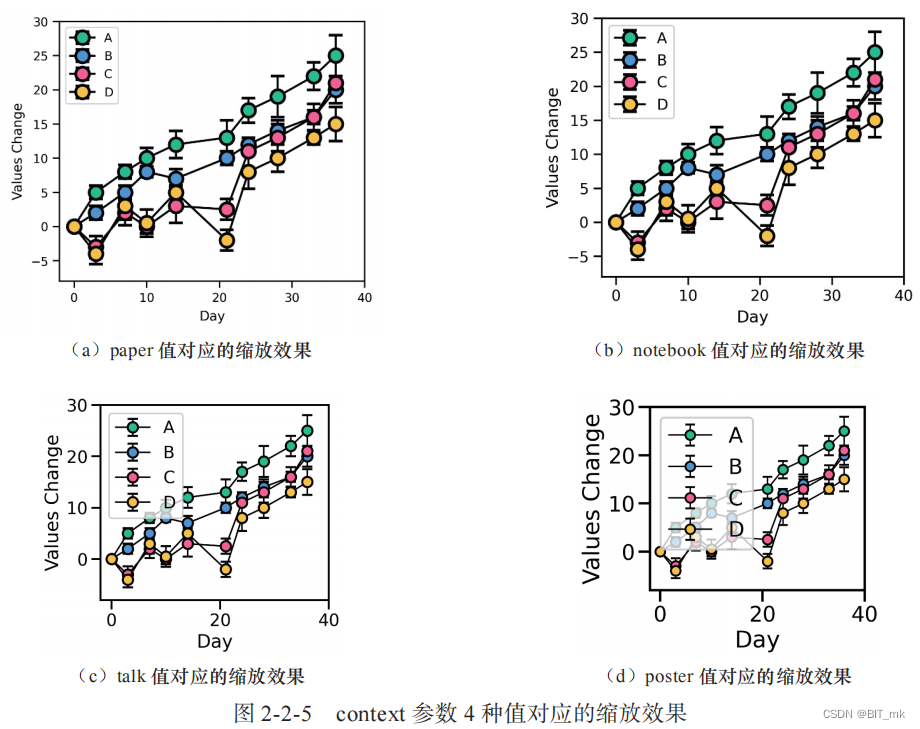
Python科研绘图--Task03
目录 图类型 关系类型图 散点图的例子 数据分布型图 rugplot例子 分类数据型图 编辑回归模型分析型图 多子图网格型图 FacetGrid() 函数 PairGrid() 函数 绘图风格、颜色主题和绘图元素缩放比例 绘图风格 颜色主题 绘图元素缩放比列 图类型 关系类型图 数据集变量…...
ssm端游游戏账号销售管理系统源码和论文
ssm端游游戏账号销售管理系统源码和论文069 开发工具:idea 数据库mysql5.7 数据库链接工具:navcat,小海豚等 技术:ssm 摘 要 互联网发展至今,无论是其理论还是技术都已经成熟,而且它广泛参与在社会中的方方面面…...
ssm+vue农家乐信息平台源码和论文
ssmvue农家乐信息平台源码和论文066 开发工具:idea 数据库mysql5.7 数据库链接工具:navcat,小海豚等 技术:ssm 1、研究现状 国外,农家乐都被作为潜在的发展农村经济,增加农民收入的重要手段,让农户广…...

安装启动yolo5教程
目录 一、下载yolo5项目 二、安装miniconda(建议不要安装在C盘) 三、安装CUDA 四、安装pytorch 五、修改配置参数 六、修改电脑参数 七、启动项目 博主硬件: Windows 10 家庭中文版 一、下载yolo5项目 GitHub - ultralytics/yolov5:…...

封装redis 分布式锁 RedisCallback
RedisCallback 是redis 一个回调接口,在 Redis 连接后执行单个命令,返回执行命令后的结果。 如果在使用 RedisCallback 时,需要自动获取 Redis 连接资源,使用完毕后并释放连接资源。 RedisTemplate 类提供了一个 execute 方法&am…...

代码随想录算法训练营第17期第32天 | 122. 买卖股票的最佳时机 II、455.分发饼干、376. 摆动序列、53. 最大子序和
122. 买卖股票的最佳时机 II 我好像记得这道题是怎么写的,也不知道是福是祸 1. 收集每天的正利润就可以,收集正利润的区间,就是股票买卖的区间,而我们只需要关注最终利润,不需要记录区间 2.局部最优:收集…...
iOS HealthKit 介绍
文章目录 一、简介二、权限配置1. 在开发者账号中勾选HealthKit2. 在targets的capabilities中添加HealthKit。3. infoPlist需要配置权限 三、创建健康数据管理类1. 引入头文件2. 健康数据读写权限3. 检查权限4. 读取步数数据5. 写入健康数据 四、运行获取权限页面 一、简介 He…...
Windows平台Unity下播放RTSP或RTMP如何开启硬解码?
我们在做Windows平台Unity播放RTMP或RTSP的时候,遇到这样的问题,比如展会、安防监控等场景下,需要同时播放多路RTMP或RTSP流,这样对设备性能,提出来更高的要求。 虽然我们软解码,已经做的资源占有非常低了…...

模板方法模式在JDBCTemplate中的应用
上一篇中系统总结了模板模式的原理和使用,提到了模板方法和回调接口。回调接口和模板方法类之间的关系可以看作服务与被服务的关系,模板方法类想要回调接口做事,就要提供相应的资源,接口用提供的资源做事,完事后&#…...
)
如何在Debian中同步系统时间?Debian 系统时间配置(NTP服务)
A. 更新源,并安装ntpdate apt-get update apt-get install ntpdate ntpdate ntp1.aliyun.com 修改时区 修改设置Linux服务器时区 方法 A 命令 : “tzselect” 方法 B 仅限于RedHat Linux 和 CentOS 命令 : “timeconfig” 方法 C 适用于Debian 命令 : “dpkg-reconfigur…...
模板方法模式(十六)
相信自己,请一定要相信自己 上一章简单介绍了代理模式(十五), 如果没有看过, 请观看上一章 一. 模板模式 引用 菜鸟教程里面的 模板模式介绍: https://www.runoob.com/design-pattern/template-pattern.html 在模板模式(Template Pattern)…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...
