蓝桥杯训练day1
前缀和+差分
- 1.前缀和
- (1)3956. 截断数组
- (2)795. 前缀和
- (3)796. 子矩阵的和
- (4)1230. K倍区间
- (5)99. 激光炸弹
- 2.差分
- (1)797. 差分
- (2)差分矩阵
- (3)3729. 改变数组元素
- (4)100. 增减序列
1.前缀和
(1)3956. 截断数组
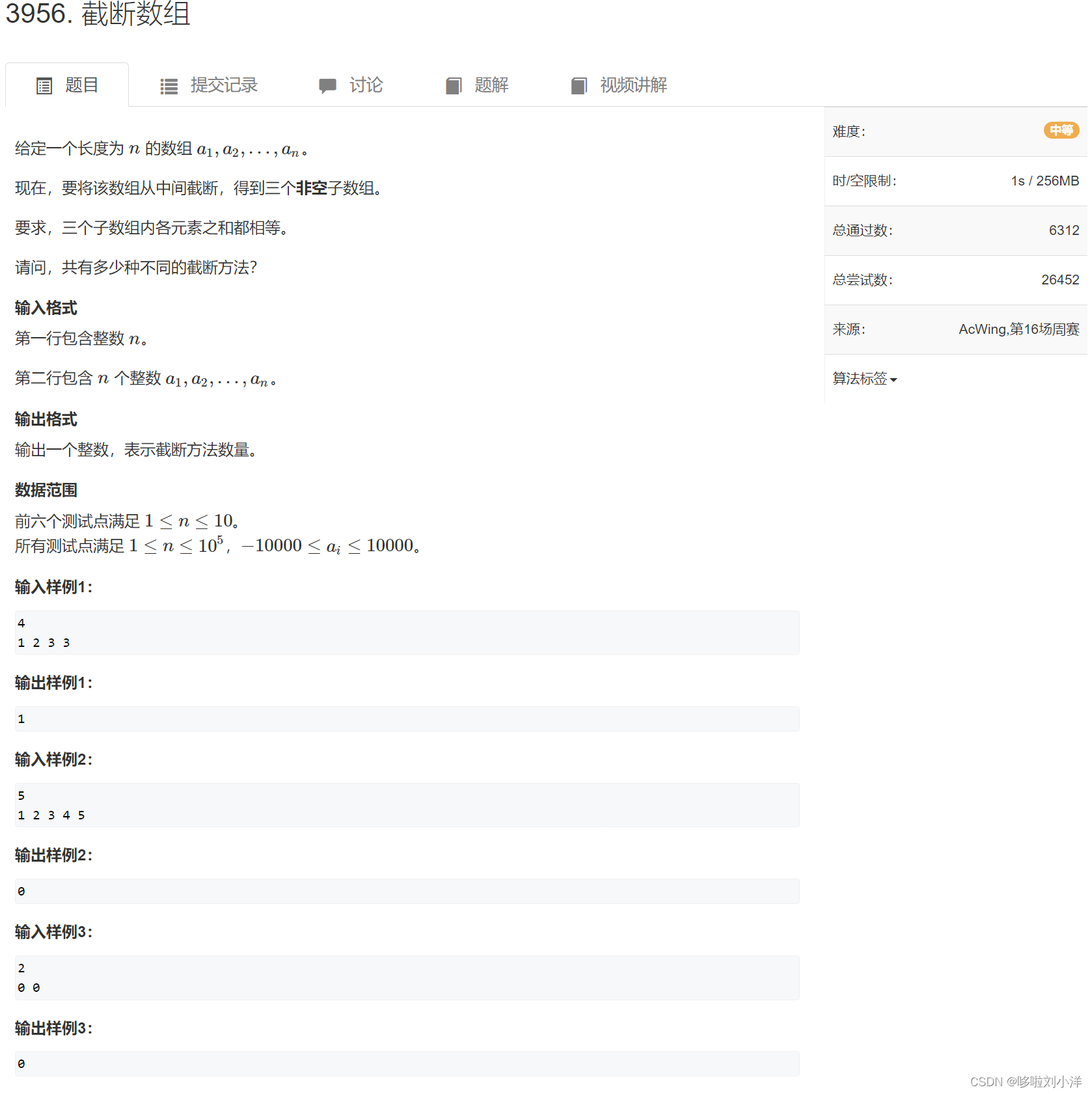
方法1:暴力
先用两个数组分别保存前缀和,后缀和。然后使用贪心思想来枚举后缀和的下标。
只有后缀和满足1/3的下标大于前缀和的下标,就加(具体看代码)过(19/22)数据
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;int n;
int a[N];
int pre[N];
int npre[N];
int h1[N], h2[N];
int cnt1, cnt2;
int sum = 0;
int main()
{cin >> n;for (int i = 1; i <= n; i++){cin >> a[i];sum += a[i];}int part = sum / 3;pre[0] = 0; //pre[i]表示前i个数的总和,这里下标从1开始有意义for (int i = 1; i <= n; i++) //前缀和{pre[i] = pre[i - 1] + a[i];if (pre[i] == part)h1[++cnt1] = i;}npre[n] = a[n];if (npre[n] == part)h2[++cnt2] = n;for (int i = n - 1; i >= 1; i--) //后缀和{npre[i] = npre[i + 1] + a[i];if (npre[i] == part)h2[++cnt2] = i;}//如此一来,存储了第一部分的part值的下标(从小到大)//又存储了第二部分的part值的下标(从大到小)//固定第二部分的下标,然后找第一部分的下标(由于从小到大,如果第二部分的下标大于第一部分下标的,则第一部分剩下的下标个数等于//当前答案个数。//然后枚举第二部分的下标,反复即可int ans = 0; //记录答案while (cnt2){int r = h2[cnt2];int temp = cnt1; //第一部分的下标while (temp){if (r > h1[temp]+1) //可以分成三个部分{ans = ans + temp;break;}temp--;}cnt2--;}cout << ans << endl;return 0;}方法2:动态规划
枚举第二部分的位置,然后找第一部分有多少分割方案。使用动态规划的技巧来减少计算
#include<iostream>
#include<cstring>
using namespace std;
const int N=100010;int n;
int cnt;
long long int ans=0;int pre[N];int main()
{cin>>n;int x;for(int i=1;i<=n;i++){cin>>x;pre[i]=pre[i-1]+x;}if(pre[n]%3){cout<<"0";return 0;}else{for(int i=2;i<=n-1;i++){if(pre[i-1]==pre[n]/3)cnt++;if(pre[i]==pre[n]/3*2)ans+=cnt;}}cout<<ans;return 0;
}(2)795. 前缀和
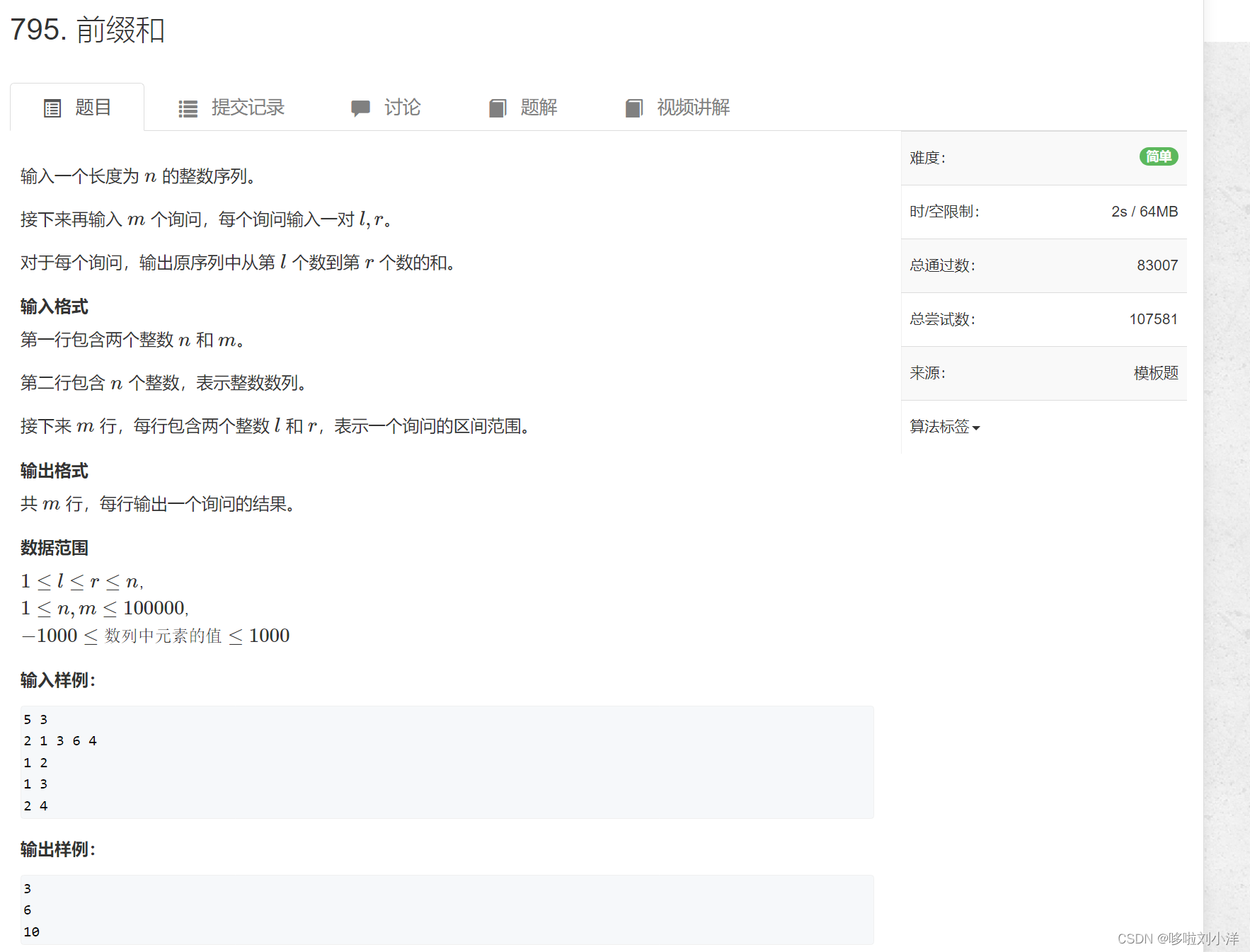
前缀和最简单的题目,模板题
用一个数组来记录前i个元素的和.
#include<iostream>
#include<cstring>
using namespace std;const int N=100010;int n,m;
int a[N];
int pre[N];int main()
{cin>>n>>m;for(int i=1;i<=n;i++) //下标从1开始{cin>>a[i];pre[i]=pre[i-1]+a[i];}while(m--){int l,r;cin>>l>>r;cout<<pre[r]-pre[l-1]<<endl; //注意是pre[l-1],要包括a[l]那个数}return 0;
}
(3)796. 子矩阵的和
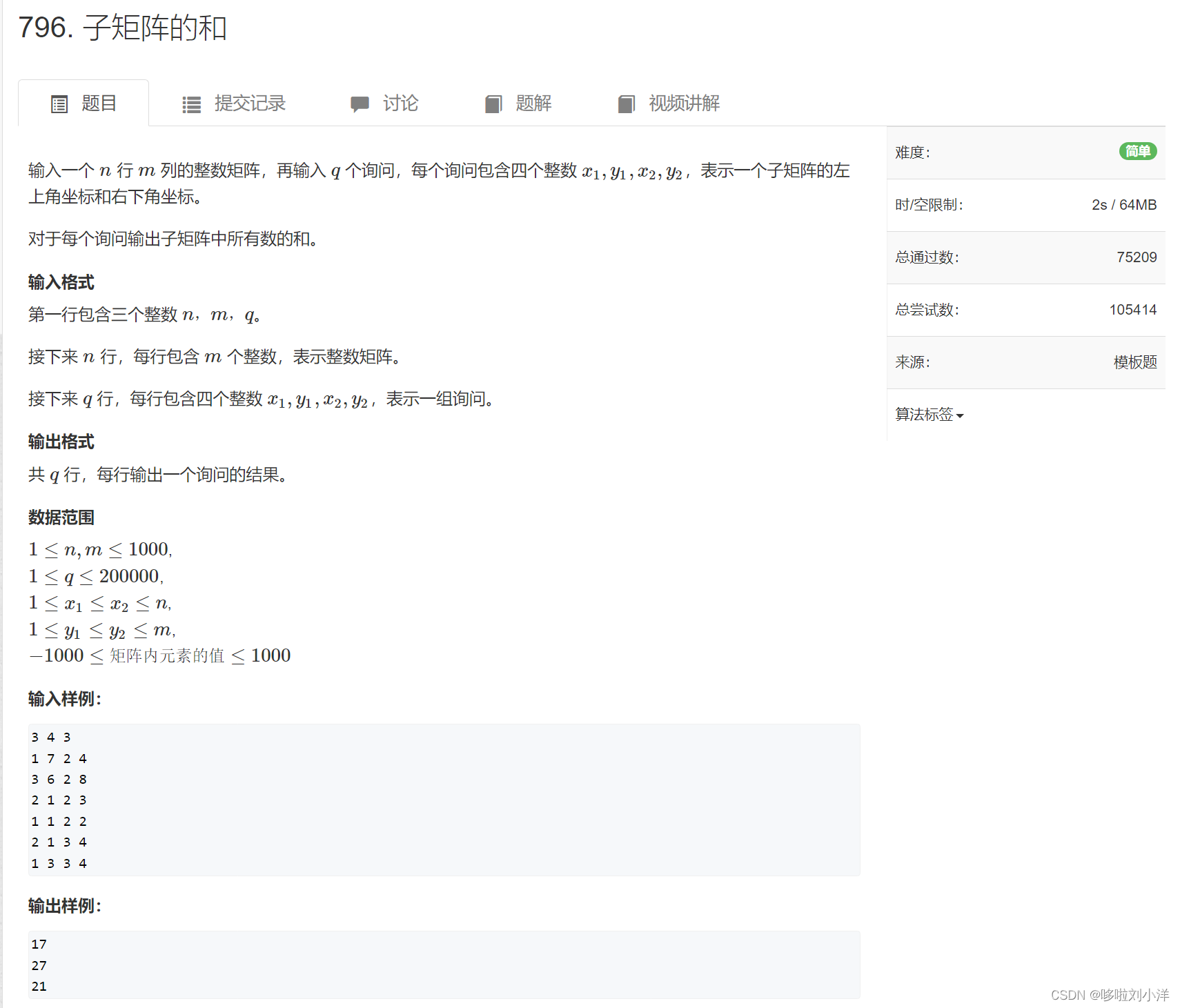
二维前缀和,
模拟过程,然后优化,反复几次即可掌握
#include<iostream>
using namespace std;const int N=1010;int g[N][N]; //矩阵
int pre[N][N]; //左上角为(1,1),右下角是(i,j)的矩阵的和int n,m,q;int main()
{cin>>n>>m>>q;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){cin>>g[i][j];pre[i][j]=pre[i][j-1]+pre[i-1][j]-pre[i-1][j-1]+g[i][j];}while(q--){int x1,x2,y1,y2;cin>>x1>>y1>>x2>>y2;cout<<pre[x2][y2]-pre[x1-1][y2]-pre[x2][y1-1]+pre[x1-1][y1-1]<<endl;}return 0;
}(4)1230. K倍区间
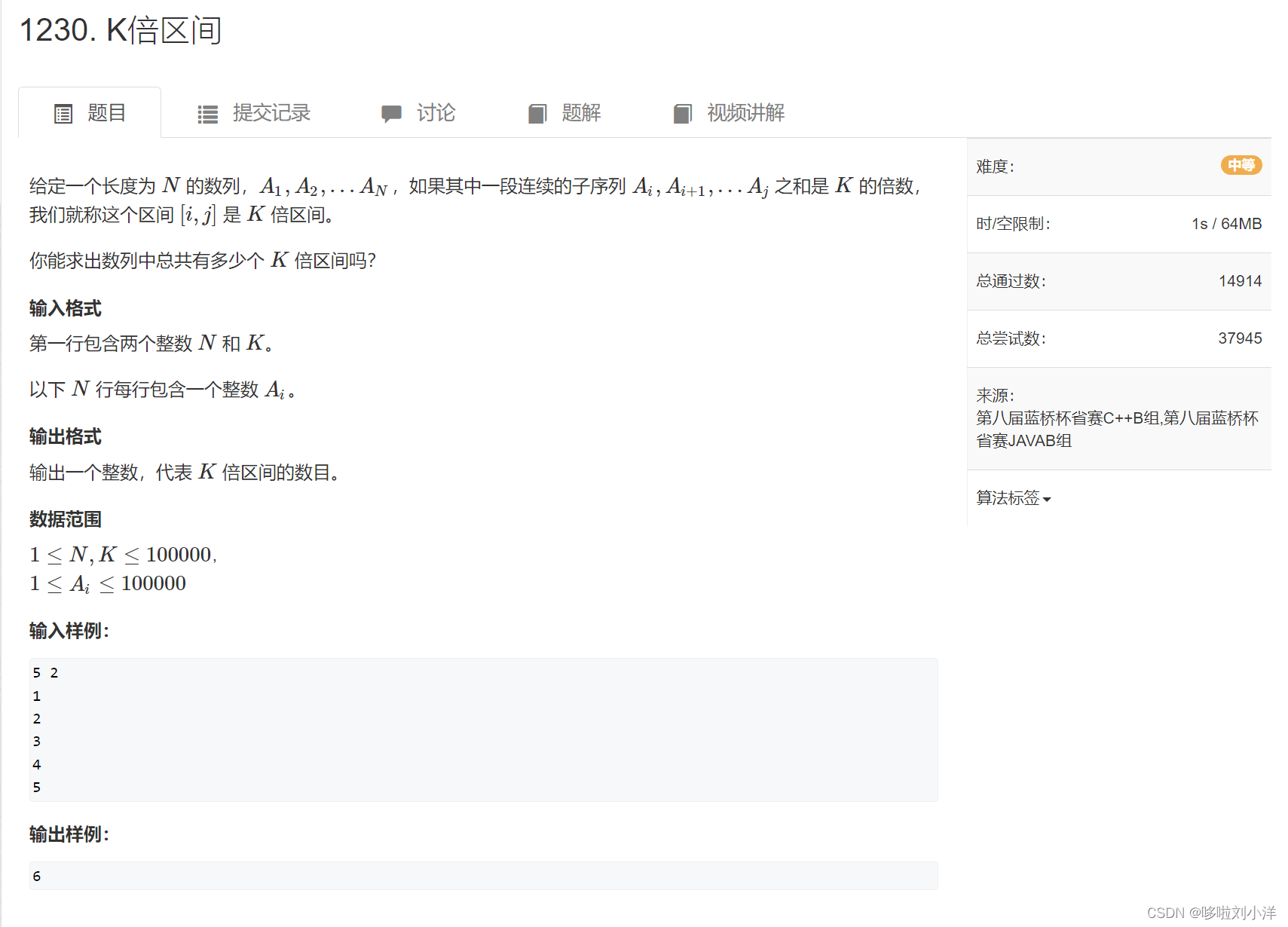
这个题目,看的第一感觉应该是个简单题,没想到是个中等题,暴力只能过一半数据。
暴力:
#include<iostream>
#include<cstring>
using namespace std;const int N=1e5+10;int n,k;int a[N];
int pre[N];
int ans=0;int main()
{cin>>n>>k;for(int i=1;i<=n;i++){cin>>a[i];a[i]%=k;pre[i]=pre[i-1]+a[i];}for(int i=1;i<=n;i++){int temp=0;for(int j=i;j<=n;j++){temp+=a[j];if(temp%k==0)ans++;}}cout<<ans;return 0;
}
想到
pre[r]-pre[l-1]=k
pre[r[=pre[l-1]+k
用pre[r]作为key,r作为key存储到哈希表,没想到也只多过一个数据
#include<iostream>
#include<cstring>
#include<unordered_map>
#include<vector>
using namespace std;const int N=1e5+10;int n,k;int a[N];
int pre[N];
int ans=0;int main()
{cin>>n>>k;unordered_map<int,vector<int>>Hash;for(int i=1;i<=n;i++){cin>>a[i];pre[i]=(pre[i-1]+a[i])%k;Hash[pre[i]].push_back(i);}//利用前缀和for(int i=1;i<=n;i++){if(Hash.count((pre[i-1]+k)%k)!=0) //找到区间{vector<int>t=Hash[(pre[i-1]+k)%k];for(int j=0;j<t.size();j++){if(i<=t[j]){ans+=t.size()-j;break;}}}}cout<<ans;return 0;
}
看了题解,发现距离答案一步之遥。在于
pre[r]-pre[l-1]=k等价于 pre[r]%k=pre[l-1]%k
所以找到两个前缀和相同的就好了,再利用一点动态规划的技巧.
#include<iostream>
using namespace std;
const int N=100010;int a[N];
int pre[N];
int Hash[N];int n,k;int main()
{cin>>n>>k;for(int i=1;i<=n;i++){cin>>a[i];pre[i]=(pre[i-1]+a[i])%k;}long long ans=0;Hash[0]=1; //由于对k取余,所以第一个元素可能就是kfor(int i=1;i<=n;i++) //从前往后遍历,到当前遍历到的点,前面有多少和他一样的值{ans+=Hash[pre[i]];Hash[pre[i]]++;}cout<<ans;return 0;}
(5)99. 激光炸弹
暴力
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;const int N=5010;int n,r;
int pre[N][N];int main()
{cin>>n>>r; //n表示目标点个数,r表示炸弹的范围r = min(r, 5001);while(n--){int x,y,v;cin>>x>>y>>v;pre[x+1][y+1]+=v;}//前缀和for(int i=1;i<=5001;i++)for(int j=1;j<=5001;j++)pre[i][j]=pre[i-1][j]+pre[i][j-1]-pre[i-1][j-1]+pre[i][j];int ans=0;//枚举右下角for(int i=r;i<=5001;i++){for(int j=r;j<=5001;j++)ans=max(ans,pre[i][j]-pre[i-r][j]-pre[i][j-r]+pre[i-r][j-r]);}cout<<ans;return 0;
}
2.差分
(1)797. 差分
什么是差分。
一句话:就是前缀和运输的逆运算.
#include<iostream>
#include<algorithm>
using namespace std;const int N=1e5+10;
int a[N];
int b[N];int n;
int T;int main()
{cin>>n>>T;for(int i=1;i<=n;i++) //相当于,b是原数组,a是b的前缀和{cin>>a[i];b[i]=a[i]-a[i-1];}while(T--){int l,r,c;cin>>l>>r>>c;b[l]+=c;b[r+1]-=c;}int sum=0;for(int i=1;i<=n;i++){sum+=b[i];cout<<sum<<" ";}return 0;
}
(2)差分矩阵

同二维前缀和一样,就是扩展一个维度(但是很难哦)
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;const int N=1010;int pre[N][N];
int a[N][N];int n,m,q;int main()
{cin>>n>>m>>q;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){cin>>pre[i][j];a[i][j]=pre[i][j]-pre[i-1][j]-pre[i][j-1]+pre[i-1][j-1];}while(q--){int x1,x2,y1,y2,c;cin>>x1>>y1>>x2>>y2>>c;a[x1][y1]+=c;a[x1][y2+1]-=c;a[x2+1][y1]-=c;a[x2+1][y2+1]+=c;}int sum=0;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){pre[i][j]=pre[i-1][j]+pre[i][j-1]-pre[i-1][j-1]+a[i][j];cout<<pre[i][j]<<" ";if(j==m)cout<<endl;}return 0;
}
(3)3729. 改变数组元素

说实话,这个题目放在差分下面,完全不知道和差分有什么关系。
就从后往前读一遍看看哪些位置可以为1就可以了,应该是个简单到不能再简单的题,,,
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;const int N=2*(1e5+10);
int a[N]; //操作数组
int b[N]; //答案数组
int T,n;//假设两个数组a,b,a是原数组,b是a的前缀和数组。
//那么a是b的差分,b是a的原数组int main()
{cin>>T;while(T--){memset(b,0,sizeof b);cin>>n;for(int i=1;i<=n;i++)cin>>a[i];int cnt=a[n];for(int i=n;i>=1;i--){cnt=max(cnt,a[i]);if(cnt>=1){b[i]=1;cnt--;}}for(int i=1;i<=n;i++)cout<<b[i]<<" ";cout<<endl;}return 0;
}
(4)100. 增减序列
这个题目难啊,由于所有的数都要一样,所有差分数组必须除了第一个数其余全是0.由于差分数组每次操作都需要b[L]+1,b[R+1]-1或b[L]-1,b[R+1]+1.所以将正数和负数相互抵消后,剩下的数要么和b[1]抵消,要么和b[n+1]抵消。
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;const int N=1e5+10;long long int a[N];
long long int b[N];int n;int main()
{cin>>n;for(int i=1;i<=n;i++){cin>>a[i];b[i]=a[i]-a[i-1];}long long int c1=0,c2=0; //c1记录正数和,c2记录负数和for(int i=2;i<=n;i++){if(b[i]>=0)c1+=b[i];else c2+=b[i];}long long int ans=min(abs(c1),abs(c2))+abs(abs(c1)-abs(c2)); //操作个数long long int count=abs(abs(c1)-abs(c2))+1;cout<<ans<<endl<<count<<endl;return 0;
}
相关文章:

蓝桥杯训练day1
前缀和差分1.前缀和(1)3956. 截断数组(2)795. 前缀和(3)796. 子矩阵的和(4)1230. K倍区间(5)99. 激光炸弹2.差分(1)797. 差分(2)差分矩阵(3)3729. 改变数组元素(4)100. 增减序列1.前缀和 (1)3956. 截断数组 方法1:暴力 先用两个数组分别保存前缀和,后缀…...

Unity毛发系统TressFX Exporter
Unity 数字人交流群:296041238 一:在Maya下的TressFX Exporter 插件安装步骤: 1. 下载Maya的TressFX Exporter插件 下载地址:TressFX Exporter 链接:https://github.com/Unity-China/cn.unity.hairfx.core/tree/m…...

《爆肝整理》保姆级系列教程python接口自动化(十九)--Json 数据处理---实战(详解)
简介 上一篇说了关于json数据处理,是为了断言方便,这篇就带各位小伙伴实战一下。首先捋一下思路,然后根据思路一步一步的去实现和实战,不要一开始就盲目的动手和无头苍蝇一样到处乱撞,撞得头破血流后而放弃了。不仅什么…...

Golang:reflect反射的使用例子
1.reflect包作用 reflect包定义了“反射”相关能力,“反射”在计算机学中是指计算机程序在运行时(runtime)可以访问、检测和修改它本身状态或行为的一种能力。基于反射特性可以通用化地解决一些需要频繁修改代码及硬编码问题,但是…...

markdown常用语法--花括号(超详细)
💌 所属专栏:【Markdown常用语法】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! …...
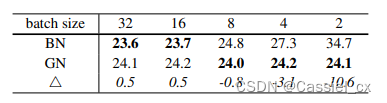
BN、SyncBN、IN、LN、GN学习记录
1 BatchNormBN的原理BN是计算机视觉最常用的标准化方法,它沿着N、H、W维度对输入特征图求均值和方差,随后再利用均值和方差来归一化特征图。计算过程如下图所示,1)沿着通道维度计算其他维度的均值;2)沿着通…...

使用 Auto-scheduling 优化算子
本篇回答来源于 TVM 官方英文文档 Lianmin Zheng,Chengfan Jia。更多 TVM 中文文档可访问→https://tvm.hyper.ai/ 本教程将展示 TVM 的 Auto Scheduling 功能,如何在不编写自定义模板的情况下,找到最佳 schedule。 与基于模板的 AutoTVM 依…...
智能运维应用之道,告别企业数字化转型危机
面临的问题及挑战 数据中心发展历程 2000 年中国数据中心始建,至今已经历以下 3 大阶段。早期:离散型数据中心 IT 因以项目建设为导向,故缺乏规划且无专门运维管理体系,此外,开发建设完的项目均是独立运维维护&#…...

第七章 SQL错误信息 - SQL错误代码 -400 到 -500
文章目录第七章 SQL错误信息 - SQL错误代码 -400 到 -500SQL错误代码和消息表WinSock错误代码-10050到-11002第七章 SQL错误信息 - SQL错误代码 -400 到 -500 SQL错误代码和消息表 错误代码描述-400发生严重错误-401严重连接错误-402用户名/密码无效-405无法从通信设备读取-4…...

DDFN: Decoupled Dynamic Filter Networks解耦的动态卷积
一、论文信息 论文名称:Decoupled Dynamic Filter Networks 论文:https://thefoxofsky.github.io/files/ddf.pdf 代码:https://github.com/theFoxofSky/ddfnet 主页:https://thefoxofsky.github.io/project_pages/ddf 作者团…...

NISP认证报名条件是什么?考试内容是什么?
科学技术是社会发展的第一生产力,每个国家为了能够获得更高的国际地位,不断提升自己的科学技术,现代最为先进的技术就是信息通信,在军事、民生、医疗、教育、制造等等领域都起着重要的作用,我们的生活也因为信息技术而…...

利用redis实现缓存、发布订阅、分布式锁功能
Redis是一个内存键值存储数据库,通常用于缓存、会话管理、消息队列等场景。以下是一些常见的Redis使用场景:1.缓存:将常用的数据缓存在Redis中,以减少对数据库的访问次数,提高应用程序的性能。2.会话管理:使…...
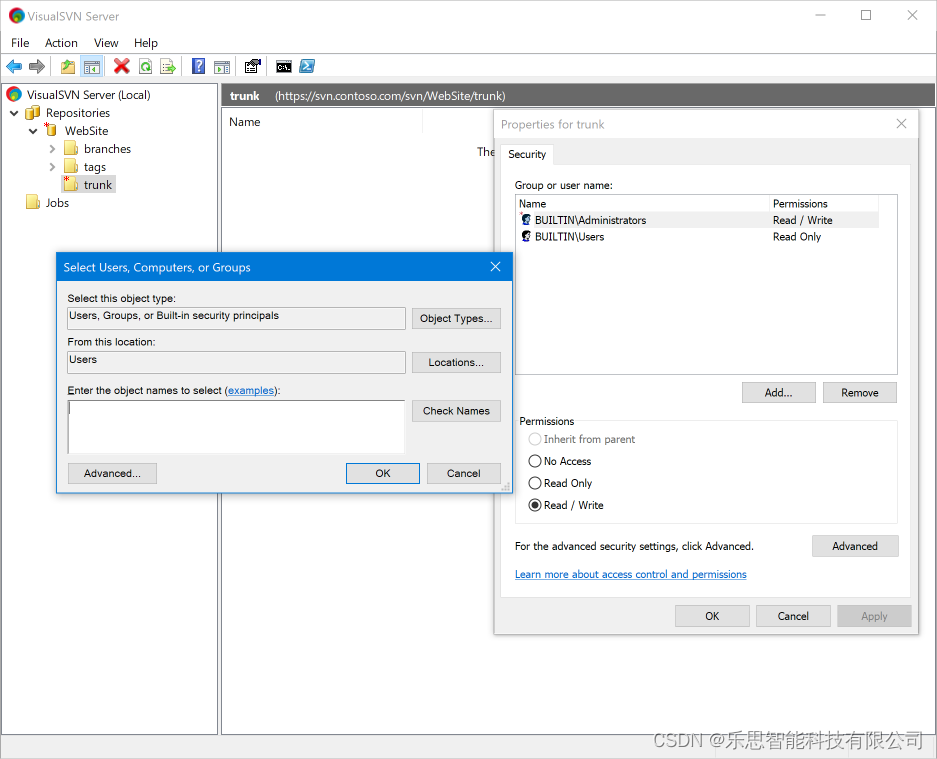
SVN无法连接到服务器的各种问题原因及解决办法
SVN专业使用教程详解 第一节 安装VisualSVN Server服务器 第一步 下载SVN服务器,需要链接的请私信。 点击下载的执行文档进行安装 选择组件 选择在部署 VisualSVN Server 时安装VisualSVN Server 和 Administration Tools 组件。 调整初始服务器配置 或者&…...

React 基本使用
目录 React 安装 React基本使用 React脚手架 脚手架使用React JSX基本使用 JSX列表渲染 JSX条件渲染 JSX模板精简 JSX样式控制 JSX综合案例 React 安装 npm i react react-domnpm init -y(生成基础目录文件) <!-- 引入js文件 --><sc…...
单例模式设计(面试题)
1、static修饰变量规则static修饰的静态成员属于 类而不是对象,所有的对象共享一份静态成员数据,所以不占用类的空间static修饰的成员,定义类的时候,必须分配空间static修饰的静态成员数据 必须类中定义 类外初始化静态成员变量可…...
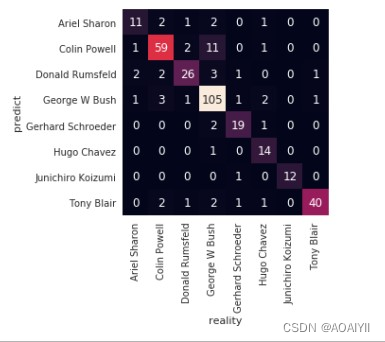
机器学习:基于支持向量机(SVM)进行人脸识别预测
机器学习:基于支持向量机(SVM)进行人脸识别预测 文章目录机器学习:基于支持向量机(SVM)进行人脸识别预测一、实验目的二、实验原理三、实验环境四、实验内容五、实验步骤1.准备数据2.业务理解3.数据理解4.数…...

【服务器数据恢复】多块磁盘离线导致RAIDZ崩溃的数据恢复案例
服务器数据恢复环境: SUN ZFS系列某型号存储阵列; 40块磁盘组建的存储池(其中4块磁盘用作全局热备盘),池内划分出若干空间映射到服务器使用; 服务器使用Windows操作系统。 服务器故障: 服务器在…...

iconfont 图标如何在uniapp中的tabBar使用
注意: 小程序并不支持tabBar中 设置 iconfont 1. 材料准备 首先进入字体图标网址:iconfont-阿里巴巴矢量图标库;(如果你没有登入,记得登入一下) 把图标添加入购物车 添加到购物车之后-(右上角…...
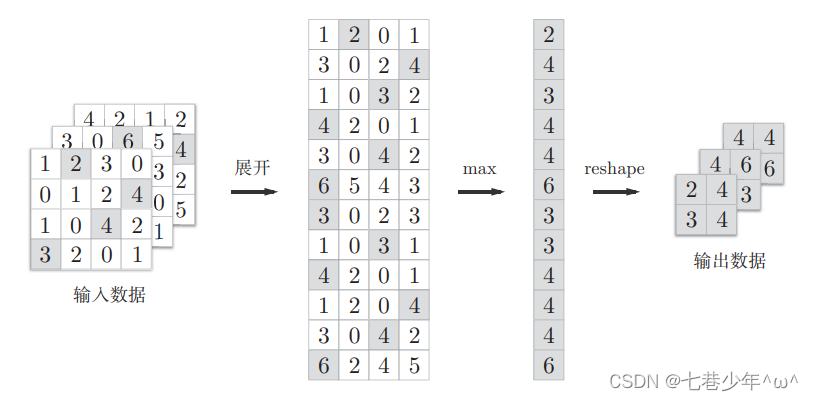
第六章.卷积神经网络(CNN)—卷积层(Convolution)池化层(Pooling)
第六章.卷积神经网络(CNN) 6.1 卷积层(Convolution)&池化层(Pooling) 1.整体结构 以5层神经网络的实现为例: 1).基于全连接层(Affine)的网络 全连接层:相邻层的所有神经元之间都有连接 2).常见的CNN的网络 3).全连接层存在的问题 数据的形状容易被…...
c/c++开发,无可避免的模板编程实践(篇六)
一、泛型算法 1.1 泛型算法概述 c标准库不仅包含数据结构(容器、容器适配器等),还有很多算法。数据结构可以帮助存放特定情况下需要保存的数据,而算法则会将数据结构中存储的数据进行变换。标准库没有给容器添加大量的功能函数&am…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...
