代码随想录训练营第四十二天|0-1背包理论基础(一)、0-1背包理论基础(二)、416分割等和子集
0-1背包理论基础(一)
文章讲解/视频链接:代码随想录
小节:本节课讲得是0-1背包的二维数组解法,dp[i][j]的含义是从物品0-i中不重复的拿出可以装进容量为j的背包的最大价值的物品,状态转移公式为,dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]),初始化时第一行第一列都要初始化,遍历时顺序可以颠倒,不影响状态转移公式,并且遍历顺序从小到大就可以。
0-1背包理论基础(二)
文章讲解/视频链接:代码随想录
小节:本节课讲得是0-1背包的一维数组解法,dp[j]的含义时容量为j的背包可以装的最大价值的物品,被题是由二维压缩过来的,主要使用了一个滚动数组,将dp[i -1]的值拷贝到dp[i]中,因此状态转移公式变为dp[j] = max(dp[j], dp[j - weight[i]] + value[i]),初始化时均为0,不像上一题可以随便初始化,本题的dp[j]求取要和自身进行比较,遍历时必须要先遍历物品,再遍历背包,如果颠倒的话,展现出来的就是每个背包只能装一个物品,在对背包进行遍历时必须要从大到小遍历,如果从小到大遍历,一个物品会被取多次,不符合题意。
背包理论小节:要理解两种情况背包的状态转移方程以及遍历顺序,是否可以颠倒遍历顺序,为什么一维遍历只能从前往后遍历,初始化等等问题。为了更好的理解问题,要自己画一画dp数组的打印值,尤其是一维滚动数组,画出来后就更好理解了。
416分割等和子集
题目链接/ 文章讲解/视频链接:代码随想录
1.代码展现
//416.分割等和子集
bool canPartition(vector<int>& nums) {//step1 构建dp数组//dp[j]的含义是背包容量为j可以装下的最大物品价值//本题的背包容量是target//这里dp数组大小之所以为10001,是因为背包容量最大为10001//因为题目中数组长度最大200,每个数最大100int nSum = 0;for (int num : nums) {nSum += num;}if (nSum % 2 == 1) return false;int nTarget = nSum / 2;vector<int> dp(nTarget + 1, 0);//step2 状态转移方程//dp[j] = max(dp[j], dp[j - weights[i]] + values[i])//本题如下,质量和价值均为nums//dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])//step3 dp数组初始化//step1中已经都初始化为0,dp[0]为0,其他初始化为0是为了//在进行遍历时不影响第一次遍历时的取值//step4 开始进行遍历for (int i = 0; i < nums.size(); i++) {for (int j = nTarget; j >= nums[i]; j--) {dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);//step5 打印数组}}if (dp[nTarget] == nTarget) return true;return false;
}
2.本题小节
思考:本题是背包问题的一种应用,可以计算数组和的一半target,这里就作为背包容量,而数组中的数字作为物品,物品中的价值和质量是一样的,这样就可以直接套背包问题的状态转移公式了,背包状态转移公式为dp[j] = max(dp[j], dp[j - weight(i)] + value(i)),进行改变后为 dp[j] = max(dp[j], dp[j - nums(i)] + nums(i)),在进行遍历时,先对数组长度进行遍历,在对target进行从大到小的遍历,注意j >= nums[i],否则没有办法装下nums[i],最后判断是否装满,也就是dp[nTarget] == nTarget时,此时只有装满了,才满足题意
相关文章:
、0-1背包理论基础(二)、416分割等和子集)
代码随想录训练营第四十二天|0-1背包理论基础(一)、0-1背包理论基础(二)、416分割等和子集
0-1背包理论基础(一) 文章讲解/视频链接:代码随想录 小节:本节课讲得是0-1背包的二维数组解法,dp[i][j]的含义是从物品0-i中不重复的拿出可以装进容量为j的背包的最大价值的物品,状态转移公式为,dp[i][j] max(dp[i - …...

linux 免交互
Linux 免交互 1、免交互概念2、基本免交互的例子2.1命令行免交互统计2.2使用脚本免交互统计2.3使用免交互命令打印2.4免交互修改密码2.5重定向查看2.6重定向到指定文件2.7重定向直接指定文件2.8使用脚本完成重定向输入2.9免交互脚本完成赋值变量2.10关闭变量替换功能࿰…...
-[文档加载器(Document Loaders)])
自然语言处理从入门到应用——LangChain:索引(Indexes)-[文档加载器(Document Loaders)]
分类目录:《自然语言处理从入门到应用》总目录 合并语言模型和我们自己的文本数据是区分它们的一种强大方式,这样做的第一步是将数据加载到“文档”中,文档加载器的作用就是使这个过程变得简单。 LangChain提供了三种文档加载器:…...
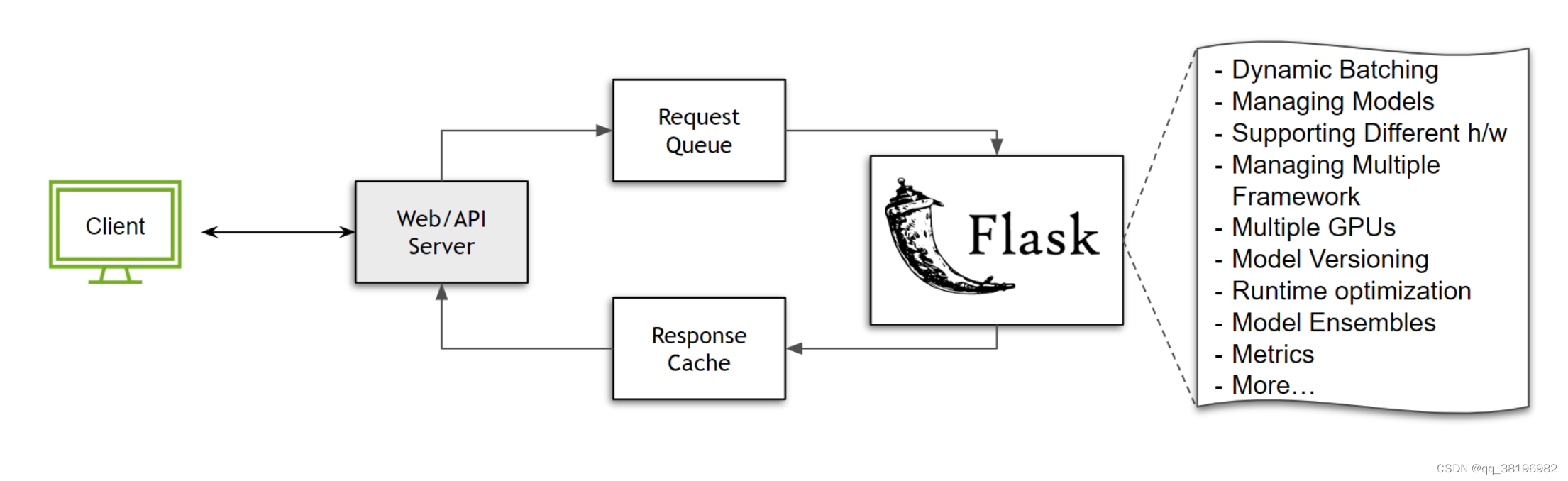
7.接着跑一下triton官方教程
5.Model Ensemble 在此示例中,我们将探索使用模型集成来仅通过单个网络调用在服务器端执行多个模型。这样做的好处是减少了在客户端和服务器之间复制数据的次数,并消除了网络调用固有的一些延迟。 为了说明创建模型集成的过程,我们将重用第…...

波奇学C++:stl的list模拟实现
list是双向带头链表。所以迭代器end()相当于哨兵卫的头。 list不支持和[]重载,原因在于list空间不是连续的,和[]的代价比较大。 访问第n个节点,只能用for循环,来实现 list<int> l; l.push_back(0); l.push_back(1); l.pu…...

Flask 项目结构
前面我们了解了 Flask 框架的特性和一些用法,比如创建一个简单应用、做些页面,以及增加鉴权模块等,如果要将 Flask 用于实际项目开发,还需要了解一下 Flask 项目结构。 Flask 是一个轻量级的 Web 框架,扩展性强&#…...

云计算在IT领域的发展和应用
文章目录 云计算的发展历程云计算的核心概念云计算在IT领域的应用1. 基础设施即服务(IaaS):2. 平台即服务(PaaS):3. 软件即服务(SaaS): 云计算的拓展应用结论 dz…...

8年测试经验之谈 —— 接口自动化测试requests
1.什么是requests? requests是一个Python第三方库,处理URL资源特别方便 2.安装requests pip3 install requests 如果遇到Permission denied安装失败,请加上sudo重试 3.使用requests 3.1get请求方法 3.1.1基本的get请求 import reques…...

求助:vue从后端获取数据,如何对获得的数据进行拆分?
从后端获取数据格式如下: { "count": 3, "lists": [ { "id": 2, "name_id": 4, "name": "4: 2201030019: 张四", }, { …...

html5拖拽文件上传需阻止默认事件
至少阻止下列3个事件的默认行为才能实现文件拖拽上传 var bdocument.getElementById(box) b.ondragenter(e)>{e.preventDefault()console.log(aaa,e.dataTransfer.files); } b.ondragover(e)>{e.preventDefault()console.log(bb,e.dataTransfer.files); }b.ondrop(e)>…...
)
深入剖析Kubernetes之Pod基本概念(一)
文章目录 Pod 中重要字段Pod 的生命周期 Pod,而不是容器,才是 Kubernetes 项目中的最小编排单位。将这个设计落实到 API 对象上,容器(Container)就成了 Pod 属性里的一个普通的字段。那么,到底哪些属性属于…...
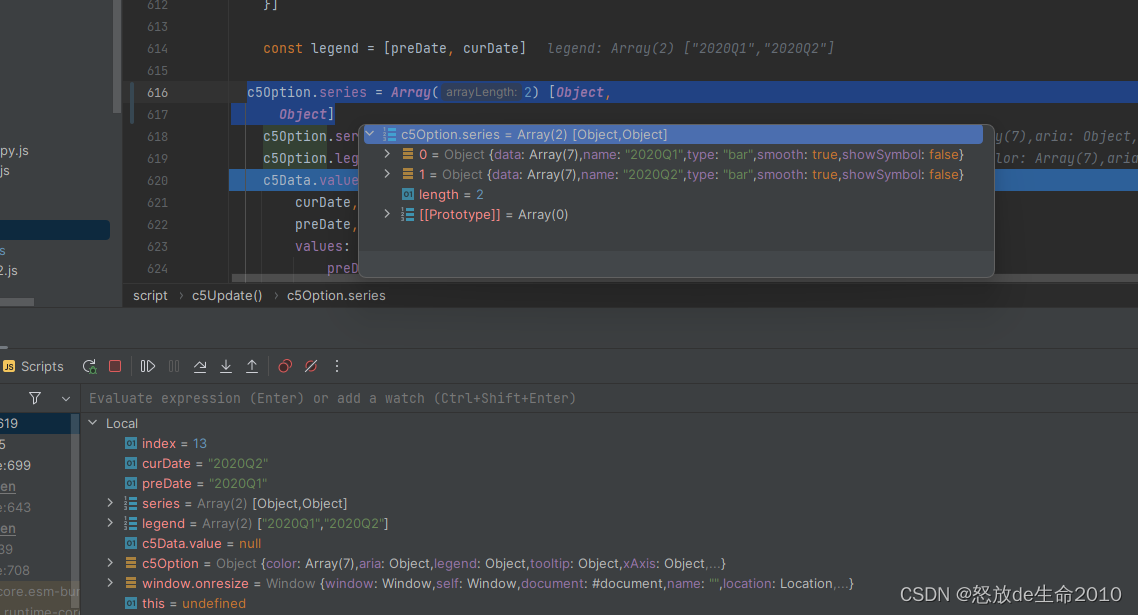
idea 对JavaScript进行debug调试
文章目录 1.新增 JavaScript Debug 配置2.配置访问地址3.访问url. 打断点测试 前言 : 工作中接手别人的前端代码没有注释,看浏览器的network或者console切来切去,很麻烦,可以试试idea自带的javscript debug功能。 1.新增 JavaScript Debug 配…...

npm init
1、什么是npm init npm是开源 JavaScript 包管理器,允许 JavaScript 开发人员分享和重用代码。npm init是一种在创建新的npm包时使用的命令,它将提示你填写一些信息以便在package.json文件中创建初始配置。 2、为什么要使用npm init初始化项目 在node…...
- 数据缓存与本地存储)
微信小程序开发教学系列(6)- 数据缓存与本地存储
第六章 数据缓存与本地存储 在开发微信小程序时,我们通常会面临一个问题:如何在不重复请求接口的情况下,将数据保存在本地,提高用户体验并减少网络请求的次数。这就需要我们学会使用数据缓存和本地存储的技巧。本章将介绍在微信小…...

跟我学c++中级篇——模板的基础术语说明
一、类模板术语 1、模板的特化 模板的特化也叫具体化,非常容易理解,就是把模板中的模板参数给定具体的类型。看下面的例子: //模板 template <typename T,typname N> class Data {}; //特化 template<> class Data<int,int&…...
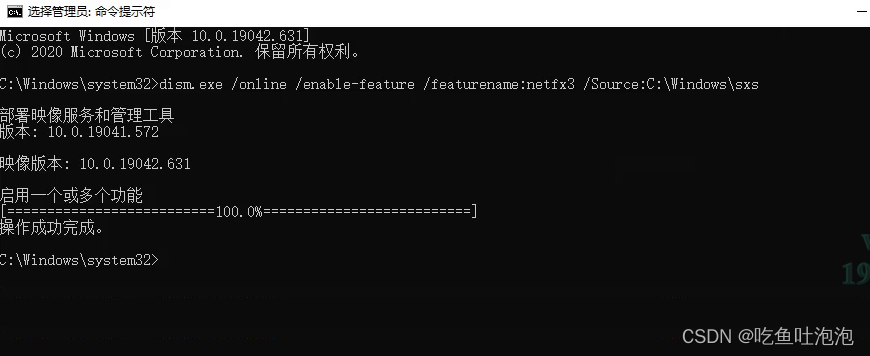
最新Win10离线安装.NET Framework 3.5的方法(附离线包2022/3/22)
win10系统安装软件时,可能需要.net framework3.5的运行环境,当我们安装某些软件的时候会提示“你的电脑上的应用需要使用以下Windows功能:.NET Framework 3.5(包括.NET 2.0和3.0)。如果系统默认的是4.0以上的版本,当软件需要.net framework3.…...

最新docker多系统安装技术
在Ubuntu操作系统中安装Docker 在Ubuntu操作系统中安装Docker的步骤如下。 1.卸载旧版本Docker 卸载旧版本Docker的命令如下: $ sudo apt-get remove docker docker-engine docker.io 2.使用脚本自动安装 在测试或开发环境中࿰…...
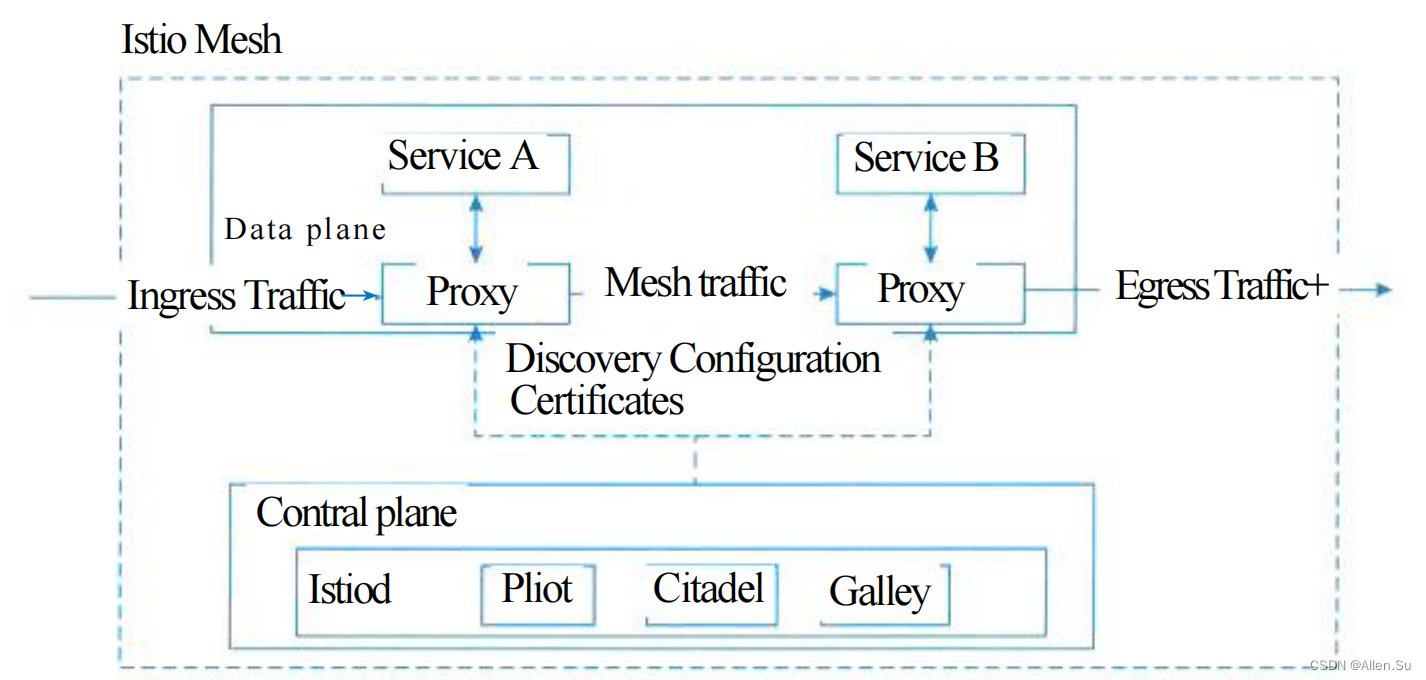
系统架构设计高级技能 · 云原生架构设计理论与实践
系列文章目录 系统架构设计高级技能 软件架构概念、架构风格、ABSD、架构复用、DSSA(一)【系统架构设计师】 系统架构设计高级技能 系统质量属性与架构评估(二)【系统架构设计师】 系统架构设计高级技能 软件可靠性分析与设计…...

Springboot集成RocketMQ——简单使用
目录 1.MQ选型 2.RocketMQ基本架构 3.Springboot集成RocketMQ 4.顺序消息 5.延时消息 6.事务消息 1.MQ选型 目前市面上的MQ选型:主要分为3个类型 Kafka:吞吐量大,且性能好,集群高可用;会丢失数据,功…...

第一百二十四回 Flexible组件
文章目录 概念介绍使用方法示例代码 我们在上一章回中介绍了扩展内容相关的知识,本章回中将介绍 Flexible组件.闲话休提,让我们一起Talk Flutter吧。 概念介绍 我们在前面章回中介绍了扩展列表相关的内容,当页面中其它组件和扩展列表一起使…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...
