【LeetCode】1223. 掷骰子模拟
1223. 掷骰子模拟
题目描述
有一个骰子模拟器会每次投掷的时候生成一个 1 到 6 的随机数。
不过我们在使用它时有个约束,就是使得投掷骰子时,连续 掷出数字 i 的次数不能超过 rollMax[i](i 从 1 开始编号)。
现在,给你一个整数数组 rollMax 和一个整数 n,请你来计算掷 n 次骰子可得到的不同点数序列的数量。
假如两个序列中至少存在一个元素不同,就认为这两个序列是不同的。由于答案可能很大,所以请返回 模 10^9 + 7 之后的结果。
示例 1
输入:n = 2, rollMax = [1,1,2,2,2,3]
输出:34
解释:我们掷 2 次骰子,如果没有约束的话,共有 6 * 6 = 36 种可能的组合。但是根据 rollMax 数组,数字 1 和 2 最多连续出现一次,所以不会出现序列 (1,1) 和 (2,2)。因此,最终答案是 36-2 = 34。
示例 2
输入:n = 2, rollMax = [1,1,1,1,1,1]
输出:30
示例 3
输入:n = 3, rollMax = [1,1,1,2,2,3]
输出:181
提示
- 1 <= n <= 5000
- rollMax.length == 6
- 1 <= rollMax[i] <= 15
算法一:动态规划
思路
-
首先,创建一个二维 dp 数组;
-
dp[i][j] 表示第 i 次掷骰子时,数字 j 出现的可能的序列总数,也就是说,第 i 次掷出的数字是 j 所有可能的序列数 , 其中 1 <= i <= n , 1 <= j <= 6 。
-
显然, dp[1][1],dp[1][2]… dp[1][6]均为 1 ,所以,最后结果有效序列总数就是 sum (dp[n][1] + dp[n][2] + … + dp[n][6]) , sum为求和函数 。
-
那么,如何计算第i次骰子掷出时,掷出数字为j的序列总数为多少呢? 仔细思考一下dp[i][j]和什么有关?
- 第一: dp[i][j] 和dp[i-1][j]有关,不仅如此,dp[i][j] 和 dp[i-1][1], dp[i-1][2],…dp[i-1][6]都有关;
- 第二: 由于连续数字限制,dp[i][j]还和 dp[i-rollMax[j-1]][1],…,dp[i-rollMax[j-1]][6]均有关;
- 所以,第i次掷出骰子的序列总数只和第i-1次掷出骰子的序列总数,以及第i-rollMax[j-1]次掷出骰子的序列总数有关。
- 详细例子看题解。
- 状态方程为 :
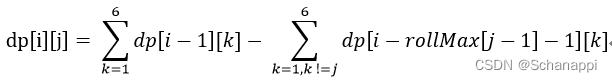
-
需要主要对大数的处理, 使用 int 型很容易越界;
-
另外,代码中有一个特殊条件的判断,当 idx == 0 时,ans 直接减一 ;此时,第 1 次 ~ 第 i - 1次掷出的都是 k ,即出现了序列 kkk…kk ,因此不合法的情况只有一种,所以减一。
算法情况
- 时间复杂度:O(6n),即O(n);
- 空间复杂度:O(7(n+1)),即 O(n)。

代码
class Solution {
public:const int MOD = 1e9 + 7;typedef long long LL;int dieSimulator(int n, vector<int>& rollMax) {vector<vector<LL> > dp(n+1, vector<LL>(7));// 初始化for (int j = 1; j <= 6; j++) {dp[1][j] = 1;}for (int i = 2; i <= n; i++) {for (int j = 1; j <= 6; j++) {// 加入第 i-1 次得所有可能序列总数LL ans = accumulate(dp[i-1].begin(), dp[i-1].end(), 0LL);int idx = i - 1 - rollMax[j-1];if (idx >= 1) {// 减去 i - 1 - rollMax[j-1]次掷出除j外其他五个数的所有序列总数ans = accumulate(dp[idx].begin(), dp[idx].end(), ans, [&](LL init, LL e) {return init + MOD - e;});ans += dp[idx][j];}else if (idx == 0) {// 特殊情况处理ans -= 1;}dp[i][j] = ans % MOD;}}return accumulate(dp[n].begin(), dp[n].end(), 0LL) % MOD;}
};参考资料:
- 超简单动态规划! 复杂度O(n)
相关文章:

【LeetCode】1223. 掷骰子模拟
1223. 掷骰子模拟 题目描述 有一个骰子模拟器会每次投掷的时候生成一个 1 到 6 的随机数。 不过我们在使用它时有个约束,就是使得投掷骰子时,连续 掷出数字 i 的次数不能超过 rollMax[i](i 从 1 开始编号)。 现在,…...

SPSS数据分析软件的安装与介绍(附网盘链接)
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
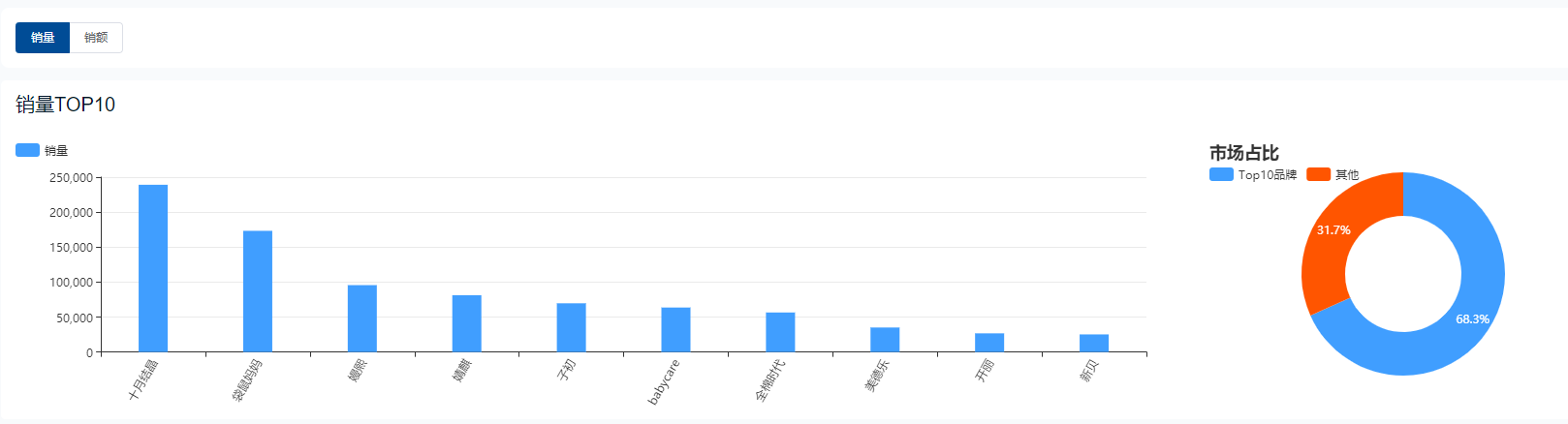
2022年38女神节大促美妆、珠宝、母婴、保健电商数据回顾
近期,我们陆续接收到了品牌商家朋友们对于2022年女神节大促期间部分品类的数据需求,希望能对今年的大促活动有一个更宏观的认知、更精准的预测,从而拿到更好的数据效果。 为此,在距离大促开启一个月的备货阶段,鲸参谋决…...

Java笔记-线程同步
目录线程的同步---以三个窗口售票100张为例方式一:同步代码块方式二:同步方法使用同步机制的作用:线程的同步—以三个窗口售票100张为例 (1)问题:卖票的过程出现重票和错票 (2)原因…...
通过python 调用OpenAI api_key提交问题解答
通过python 调用OpenAI api_key提交问题解答✨可以通过网页版的jupyter notebook调用,也可以通过spyder窗口等IDE窗口. 🌼通过python 调用OpenAI api_key接口,可以避免国内网页不能访问的问题。前提是需要自己已经注册了OpenAI帐号ÿ…...
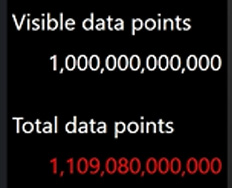
图表控件LightningChart .NET再破世界纪录,支持实时可视化 1 万亿个数据点
LightningChart.NET SDK 是一款高性能数据可视化插件工具,由数据可视化软件组件和工具类组成,可支持基于 Windows 的用户界面框架(Windows Presentation Foundation)、Windows 通用应用平台(Universal Windows Platfor…...
什么是响应性?
响应性: 这个术语在今天的各种编程讨论中经常出现,但人们说它的时候究竟是想表达什么意思呢?本质上,响应性是一种可以使我们声明式地处理变化的编程范式。一个经常被拿来当作典型例子的用例即是 Excel 表格: 这里单元…...
黑马】后台管理176-183
一、新建订单管理的分支二、创建一个订单管理的vue文件进行组件页面的路由配置import Order from ../components/order/Order.vue{path:/orders,component:Order},注意上面的components不要忘记少加一个s!三,获取后台数据面包屑导航粘贴过来文本输入框&a…...
通俗易懂详细教程)
Typescript - 类型守卫(typeof / in / instanceof / 自定义类型保护的类型谓词)通俗易懂详细教程
前言 类型守卫用于获取变量类型信息,通常使用在条件块语句中。类型守卫是返回布尔值的常规函数,接受一个类型并告诉 TypeScript 是否可以缩小到更具体的类型。类型守卫具有唯一的属性,可以确保测试的值返回的是布尔值类型。 TypeScript 使用了…...

6.8 左特征向量
特征值很复杂,除了普通的特征向量外,还有左特征向量和广义特征向量。先说说比较容易的左特征向量吧。它是这样定义的,AAA是一个矩阵,λ\lambdaλ是它的一个特征值,下面的向量yyy就是矩阵关于特征值的左特征向量left ei…...
10个自动化测试框架,测试工程师用起来
软件行业正迈向自主、快速、高效的未来。为了跟上这个高速前进的生态系统的步伐,必须加快应用程序的交付时间,但不能以牺牲质量为代价。快速实现质量是必要的,因此质量保证得到了很多关注。为了满足卓越的质量和更快的上市时间的需求…...

城市C友会【官方牵头更多的线下交流的机会,你有怎样的期待?】
文章目录🌟 课前小差🌟 长沙线下🌟 C友会你也可以是组织者🌟 线下交流提升价值🌟 官方与抖音合作?🌟 23年动起来🌟 写在最后🌟 课前小差 哈喽,大家好&#x…...

CSDN 编程竞赛二十七期题解
竞赛总览 CSDN 编程竞赛二十七期:比赛详情 (csdn.net) 四道题都不难,本来十分钟内就可以解决,但是这次竞赛bug比较多,体验不是很好。 竞赛题解 题目1、幸运数字 小艺定义一个幸运数字的标准包含三条:1、仅包含4或…...

RMI攻击中的ServerClient相互攻击反制
前言 前文中,我们分析了攻击Registry的两种方式,这里我们接着前面的内容,分析Server和Client的相互攻击方式。 Attacked Server Attacked By Client 首先我们搭建个示例,这里直接注册端和服务端放置在一起。 package pers.rm…...

值类型和引用类型
一、值类型和引用类型示例: 值类型:基本数据类型系列,如:int,float,bool,string,数组和结构体等。 引用类型:如:指针,slice切片,map&a…...
后端开发必懂nginx面试40问
什么是Nginx? Nginx是一个 轻量级/高性能的反向代理Web服务器,用于 HTTP、HTTPS、SMTP、POP3 和 IMAP 协议。他实现非常高效的反向代理、负载平衡,他可以处理2-3万并发连接数,官方监测能支持5万并发,现在中国使用ngin…...

Redis为什么这么快?
1.基于内存存储实现 在MySQL数据库中,所有的读写操作都要通过IO的方式从硬盘中获取。在Redis中,所有的操作都是基于内存实现的,从而减少IO操作提高数据库性能。 2.高效的数据结构 SAS简单动态字符串 字符串长度:SAS查询的时间复杂度O(1),c语言中时间复杂度O(n)空间分配来…...
几种实现主题切换的方式
几种实现主题切换的方式 1. 利用 prefers-color-scheme 特性 prefers-color-scheme是CSS 媒体特性【media】用于检测用户是否有将操作系统的主题色设置为亮色【light】或者暗色【dark】。 当前prefers-color-scheme新特性支持各大主流电脑(window和IOS系统&#…...
Jenkins使用(代码拉取->编译构建->部署上线)
Jenkins简介 Jenkins是一个开源项目,提供了一种易于使用的持续集成系统,使开发者从繁杂的集成中解脱出来,专注于更重要的业务逻辑实现上。同时Jenkins能实时监控集成中存在的错误,提供详细的日志文件和提醒功能,还能用…...

IEEE期刊论文投稿前期准备
目录 1、简介 2、资料准备 TPAMI 投稿须知 Letex模板资料下载 下载参考文献Bib文件...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
