matlab使用教程(26)—常微分方程的求解
1.求解非刚性 ODE
2.1 示例:非刚性 van der Pol 方程

dydt = odefun(t,y)
function dydt = vdp1(t,y)
%VDP1 Evaluate the van der Pol ODEs for mu = 1
%
% See also ODE113, ODE23, ODE45.
% Jacek Kierzenka and Lawrence F. Shampine
% Copyright 1984-2014 The MathWorks, Inc.
dydt = [y(2); (1-y(1)^2)*y(2)-y(1)];[t,y] = ode45(@vdp1,[0 20],[2; 0]);plot(t,y(:,1),'-o',t,y(:,2),'-o')
title('Solution of van der Pol Equation (\mu = 1) using ODE45');
xlabel('Time t');
ylabel('Solution y');
legend('y_1','y_2')
2.2 示例:非刚性欧拉方程

function rigidode
%RIGIDODE Euler equations of a rigid body without external forces.
% A standard test problem for non-stiff solvers proposed by Krogh. The
% analytical solutions are Jacobian elliptic functions, accessible in
% MATLAB. The interval here is about 1.5 periods; it is that for which
% solutions are plotted on p. 243 of Shampine and Gordon.
%
% L. F. Shampine and M. K. Gordon, Computer Solution of Ordinary
% Differential Equations, W.H. Freeman & Co., 1975.
%
% See also ODE45, ODE23, ODE113, FUNCTION_HANDLE.
% Mark W. Reichelt and Lawrence F. Shampine, 3-23-94, 4-19-94
% Copyright 1984-2014 The MathWorks, Inc.
tspan = [0 12];
y0 = [0; 1; 1];
% solve the problem using ODE45
figure;
ode45(@f,tspan,y0);
% --------------------------------------------------------------------------
function dydt = f(t,y)
dydt = [ y(2)*y(3)-y(1)*y(3)-0.51*y(1)*y(2) ];rigidode
title('Solution of Rigid Body w/o External Forces using ODE45')
legend('y_1','y_2','y_3','Location','Best')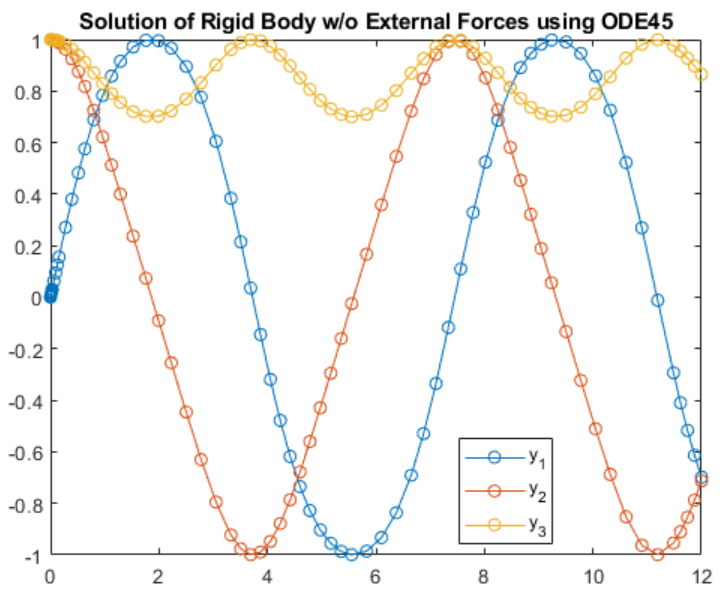
2.求解刚性 ODE
2.1 什么是刚性 ODE?
2.2 求解器选项
2.3 示例:刚性 van der Pol 方程

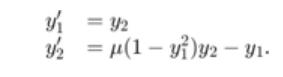
function dydt = vdp1000(t,y)
%VDP1000 Evaluate the van der Pol ODEs for mu = 1000.
%
% See also ODE15S, ODE23S, ODE23T, ODE23TB.
% Jacek Kierzenka and Lawrence F. Shampine
% Copyright 1984-2014 The MathWorks, Inc.
dydt = [y(2); 1000*(1-y(1)^2)*y(2)-y(1)];[t,y] = ode15s(@vdp1000,[0 3000],[2; 0]);
plot(t,y(:,1),'-o');
title('Solution of van der Pol Equation, \mu = 1000');
xlabel('Time t');
ylabel('Solution y_1');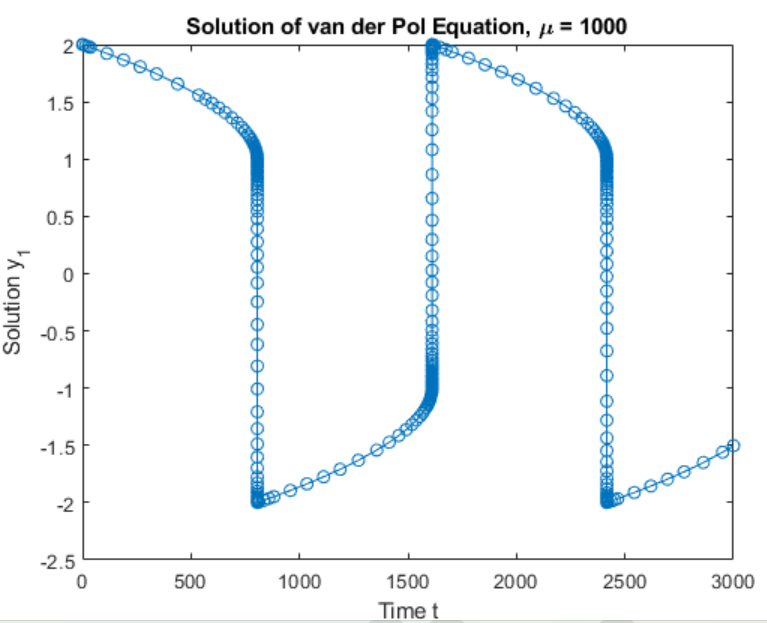
2.4 示例:稀疏 Brusselator 方程组
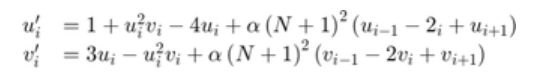

function brussode(N)
%BRUSSODE Stiff problem modelling a chemical reaction (the Brusselator).
% The parameter N >= 2 is used to specify the number of grid points; the
% resulting system consists of 2N equations. By default, N is 20. The
% problem becomes increasingly stiff and increasingly sparse as N is
% increased. The Jacobian for this problem is a sparse constant matrix
% (banded with bandwidth 5).
%
% The property 'JPattern' is used to provide the solver with a sparse
% matrix of 1's and 0's showing the locations of nonzeros in the Jacobian
% df/dy. By default, the stiff solvers of the ODE Suite generate Jacobians
% numerically as full matrices. However, when a sparsity pattern is
% provided, the solver uses it to generate the Jacobian numerically as a
% sparse matrix. Providing a sparsity pattern can significantly reduce the
% number of function evaluations required to generate the Jacobian and can
% accelerate integration. For the BRUSSODE problem, only 4 evaluations of
% the function are needed to compute the 2N x 2N Jacobian matrix.
%
% Setting the 'Vectorized' property indicates the function f is
% vectorized.
%
% E. Hairer and G. Wanner, Solving Ordinary Differential Equations II,
% Stiff and Differential-Algebraic Problems, Springer-Verlag, Berlin,
% 1991, pp. 5-8.
%
% See also ODE15S, ODE23S, ODE23T, ODE23TB, ODESET, FUNCTION_HANDLE.
% Mark W. Reichelt and Lawrence F. Shampine, 8-30-94
% Copyright 1984-2014 The MathWorks, Inc.
% Problem parameter, shared with the nested function.
if nargin<1
N = 20;
end
tspan = [0; 10];
y0 = [1+sin((2*pi/(N+1))*(1:N)); repmat(3,1,N)];
options = odeset('Vectorized','on','JPattern',jpattern(N));
[t,y] = ode15s(@f,tspan,y0,options);
u = y(:,1:2:end);
x = (1:N)/(N+1);
figure;
surf(x,t,u);
view(-40,30);
xlabel('space');
ylabel('time');
zlabel('solution u');
title(['The Brusselator for N = ' num2str(N)]);
% -------------------------------------------------------------------------
% Nested function -- N is provided by the outer function.
%
function dydt = f(t,y)
% Derivative function
c = 0.02 * (N+1)^2;
dydt = zeros(2*N,size(y,2)); % preallocate dy/dt% Evaluate the 2 components of the function at one edge of the grid
% (with edge conditions).
i = 1;
dydt(i,:) = 1 + y(i+1,:).*y(i,:).^2 - 4*y(i,:) + c*(1-2*y(i,:)+y(i+2,:));
dydt(i+1,:) = 3*y(i,:) - y(i+1,:).*y(i,:).^2 + c*(3-2*y(i+1,:)+y(i+3,:));% Evaluate the 2 components of the function at all interior grid points.
i = 3:2:2*N-3;
dydt(i,:) = 1 + y(i+1,:).*y(i,:).^2 - 4*y(i,:) + ...
c*(y(i-2,:)-2*y(i,:)+y(i+2,:));
dydt(i+1,:) = 3*y(i,:) - y(i+1,:).*y(i,:).^2 + ...
c*(y(i-1,:)-2*y(i+1,:)+y(i+3,:));% Evaluate the 2 components of the function at the other edge of the grid
% (with edge conditions).
i = 2*N-1;
dydt(i,:) = 1 + y(i+1,:).*y(i,:).^2 - 4*y(i,:) + c*(y(i-2,:)-2*y(i,:)+1);
dydt(i+1,:) = 3*y(i,:) - y(i+1,:).*y(i,:).^2 + c*(y(i-1,:)-2*y(i+1,:)+3);
end
% -------------------------------------------------------------------------
end % brussode% ---------------------------------------------------------------------------
% Subfunction -- the sparsity pattern
%
function S = jpattern(N)
% Jacobian sparsity pattern
B = ones(2*N,5);
B(2:2:2*N,2) = zeros(N,1);
B(1:2:2*N-1,4) = zeros(N,1);
S = spdiags(B,-2:2,2*N,2*N);
end
% ---------------------------------------------------------------------------brussode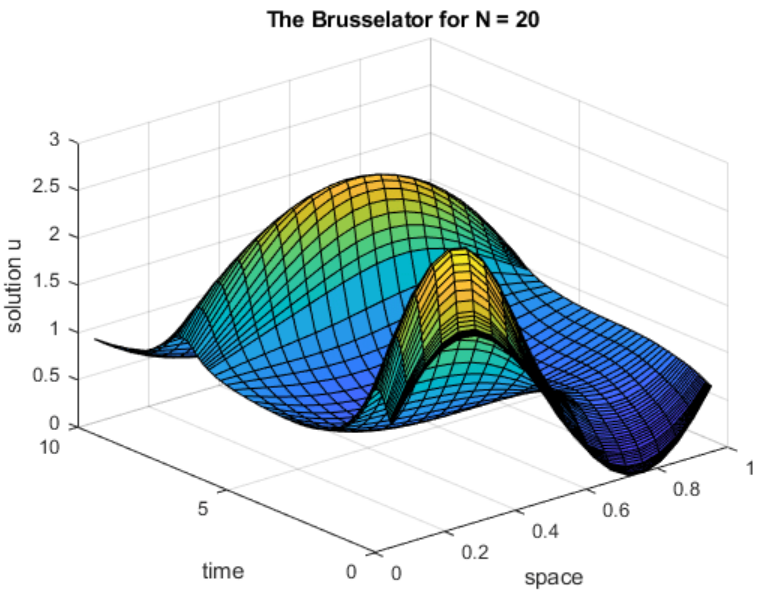
brussode(50)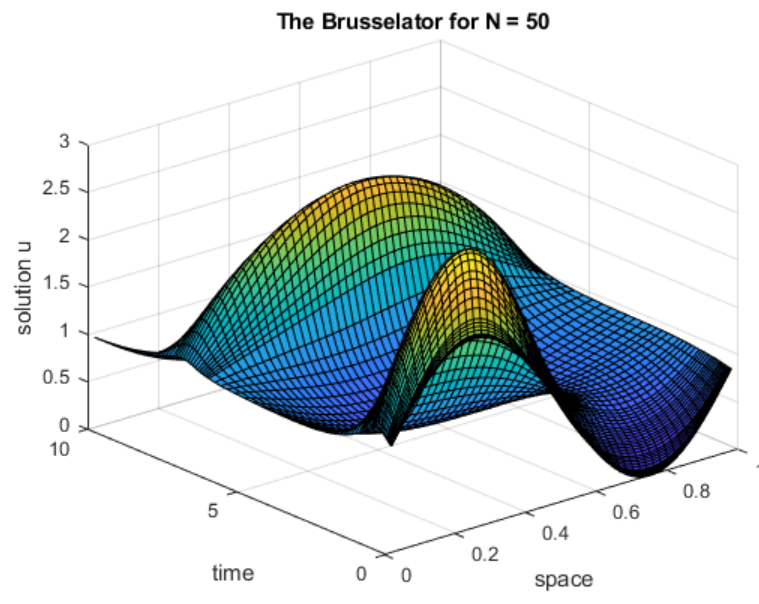
相关文章:

matlab使用教程(26)—常微分方程的求解
1.求解非刚性 ODE 本页包含两个使用 ode45 来求解非刚性常微分方程的示例。MATLAB 提供几个非刚性 ODE 求解器。 • ode45 • ode23 • ode78 • ode89 • ode113 对于大多数非刚性问题,ode45 的性能最佳。但对于允许较宽松的误差容限或刚度适中的问题&…...

尚硅谷宋红康MySQL笔记 14-18
是记录,不会太详细,受本人知识限制会有错误,会有个人的理解在里面 第14章 视图 了解一下,数据库的常见对象 对象描述表(TABLE)表是存储数据的逻辑单元,以行和列的形式存在,列就是字段,行就是记…...
香港全新的虚拟资产服务商发牌制度
香港证监会2023年2月20日通告,原有虛擬資產交易平台如要符合資格參與當作為獲發牌的安排,必須在2023 年6 月1 日至2024 年2 月29 日期間(即由2023 年6 月1 日37起計九個月內)內,根據《打擊洗錢條例》下的虛擬資產服務提供者制度在網上提交完全…...

C# 泛型
目录 一、前言 二、相关内容 1、什么是泛型? 2、泛型类 3、泛型方法 4、限定类型参数 4.1、 类型参数的基本约束 4.2、接口约束 4.3、基类约束 4.5、泛型参数与限定类型参数的关系 4.6、自定义约束 5、使用泛型的好处 5.1、代码复用性 5.2、类型安全…...
servlet,Filter,责任的设计模式,静态代理
servlet servlet是前端和数据库交互的一个桥梁 静态网页资源的技术:在前端整个运行的过程中 我们的网页代码不发生改变的这种情况就称为静态的网页资源技术动态网页资源的技术:在前端运行的过程中 我们的前端页面代码会发生改变的这种情况就称为 动态的网…...
:按位运算符(上))
C++中的运算符总结(5):按位运算符(上)
C中的运算符总结(5):按位运算符(上) 9、按位运算符 NOT( ~)、 AND( &)、 OR( |)和 XOR( ^) 逻辑运算符和…...

8.Oracle中多表连接查询方式
表连接分类: 内连接、外连接、交叉连接、自连接 1 内连接 内连接是一种常见的多表关联查询方式,一般使用关键字INNER JOIN来实现。其中,INNER关键字可以省略,当只使用JOIN关键字时,语句只表示内连接操作。在使用内连…...
Linux 安装mysql(ARM架构)
添加mysql用户组和mysql用户 安装依赖libaio yum install -y libaio* 下载Mysql wget https://obs.cn-north-4.myhuaweicloud.com/obs-mirror-ftp4/database/mysql-5.7.27-aarch64.tar.gz安装mysql 解压Mysql tar xvf mysql-5.7.27-aarch64.tar.gz -C /usr/local/ 重命名 …...

git:git clone报错提示permissions xxxx for xxxxxx are too open
问题: 如题 参考: [密钥权限过大错误]ssh “permissions are too open” error 解决办法: 将id_rsa和id_rsa.pub的权限改为600...

elasticSearch数据的导入和导出
http://wget https://nodejs.org/dist/v10.13.0/node-v10.13.0-linux-x64.tar.gz 解压即可: 1、将索引中的数据导出到本地 myindex 是我的索引 elasticdump --inputhttp://localhost:9200/myindex--output/home/date/myindex.json2、将本地数据导入es中 elasticdum…...

DDR PHY
1.ddr phy架构 1.pub(phy unility block) 支持特性: (1)不支持SDRAM的DLL off mode (2)数据位宽是以8bit逐渐递增的(这样做的目的是因为可能支持16/32/64bit的总线位宽ÿ…...

XSS攻击是怎么回事?记录一下
title: XSS攻击 date: 2023-08-27 19:15:57 tags: [XSS, 网络安全] categories: 网络安全 今天学习了一个网络攻击的手段,XSS攻击技术,大家自建网站的朋友,记得看看是否有此漏洞。 🎈 XSS 攻击 全称跨站脚本攻击 Cross Site Sc…...
FFmpeg支持多线程编码并保存mp4文件示例
之前介绍的示例: (1).https://blog.csdn.net/fengbingchun/article/details/132129988 中对编码后数据保存成mp4 (2).https://blog.csdn.net/fengbingchun/article/details/132128885 中通过AVIOContext实现从内存读取数据 (3).https://blog.csdn.net/fengbingchun/…...
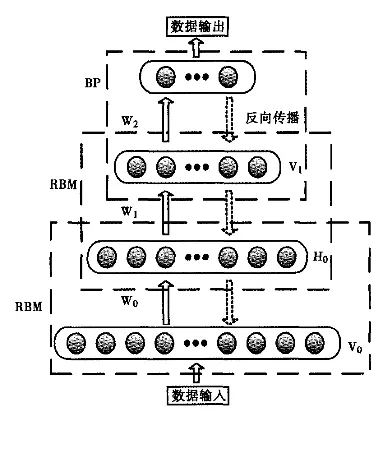
一文搞懂深度信念网络!DBN概念介绍与Pytorch实战
目录 一、概述1.1 深度信念网络的概述1.2 深度信念网络与其他深度学习模型的比较结构层次学习方式训练和优化应用领域 1.3 应用领域图像识别与处理自然语言处理推荐系统语音识别无监督学习与异常检测药物发现与生物信息学 二、结构2.1 受限玻尔兹曼机(RBM࿰…...

MyBatis:使用注解让数据库操作更简单
目录 一、简介 二、配置 三、基于注解的基本使用 四、测试 总结 一、简介 在Java开发中,数据库操作是一个常见而重要的任务。为了方便地执行SQL语句,获取结果集,处理异常等,我们通常需要使用JDBC(Java Database …...
基于PyTorch深度学习遥感影像地物分类与目标检测、分割及遥感影像问题深度学习优化
我国高分辨率对地观测系统重大专项已全面启动,高空间、高光谱、高时间分辨率和宽地面覆盖于一体的全球天空地一体化立体对地观测网逐步形成,将成为保障国家安全的基础性和战略性资源。未来10年全球每天获取的观测数据将超过10PB,遥感大数据时…...
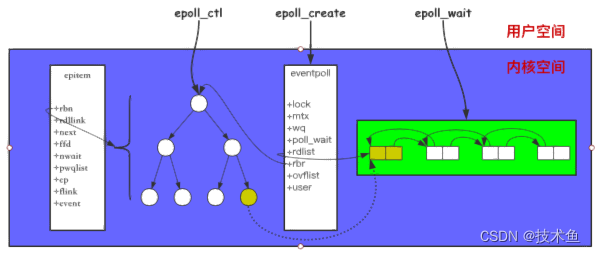
4.网络设计与redis、memcached、nginx组件(一)
网络组件系列文章目录 第四章 网络设计与redis、memcached、nginx组件 文章目录 网络组件系列文章目录文章的思维导图前言一、网络相关的问题,网络开发中要处理那些问题?网络操作IO连接建立连接断开消息到达消息发送网络操作IO特性 二、网络中IO检测IO函…...

leetcode分类刷题:矩阵顺时针模拟
1、这种题目是对代码熟练度考察,模拟顺时针建立或访问矩阵,需要注意矩阵是否为方阵 2、具体思路:以圈数为循环条件,每一圈都坚持左闭右开的区间规则;当小的行列值为奇数,最后一圈为一行或一列或一个数字的不…...

Java8新特性整理记录
1、list实体集合根据某个属性分组后求和 方法一: list.stream().collect(Collectors.groupingBy(e -> e.getId())).values().stream().map(d -> {DemoEntity sampleData d.get(0);sampleData.setPremium(d.stream().map(s -> new BigDecimal(s.getPrem…...

43.227.196.1 RAID技术有什么意义?
RAID(Redundant Array of Inexpensive Disks)技术是一种数据存储技术,它通过将多个硬盘组合在一起,来提高数据存储的性能、可靠性和容错性。 RAID技术的主要意义包括: 提高数据读写性能:RAID技术可以将多…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...
