【C语言】位操作符的一些题目与技巧
初学者在学完位操作符之后,总是不能很好的掌握,因此这篇文章旨在巩固对位操作符的理解与使用。
有的题目可能会比较难以接受,但是看完一定会有收获
目录
- 位操作符:
- 一些题目:
- 不创建临时变量交换整数
- 整数转换
- 二进制中1的个数
- 不用加减乘除实现加法
- 寻找奇数
- 错误的集合(必看)
- 小技巧:
- 总结:
位操作符:
开始之前,先来了解一下位操作符
&按位与,只有两个数
同时为真才为真,否则为假
| 按位或,只有两个数同时为假才为假,否则为真
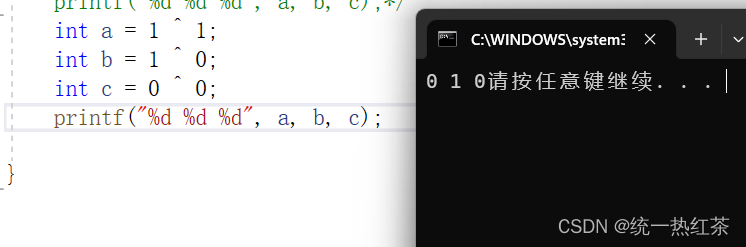
^按位异或,两个数相同为0,不同为0
- 例子:
- 按位与:
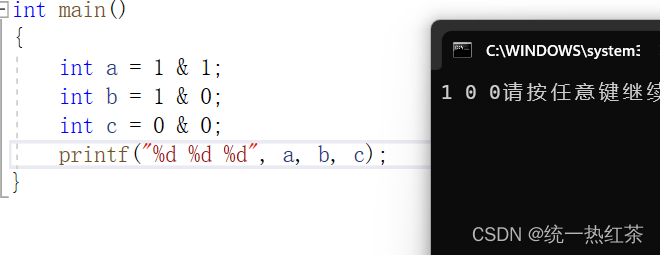
- 按位或:
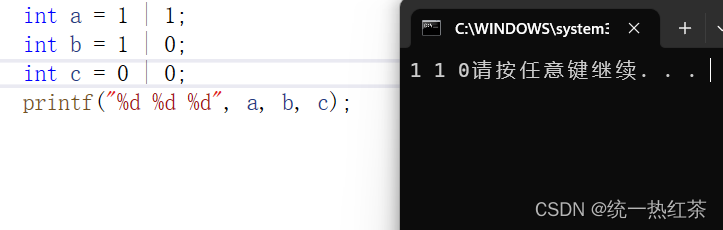
- 按位异或:
一些题目:
题目大都来自牛客与力扣,虽然不能很好的囊括位操作符的全部,但是可以很好的加深理解。
一一一一一一一一一一一一一一分割线一一一一一一一一一一一一一一
不创建临时变量交换整数
注意:此题无链接
不能创建临时变量(第三个变量),实现两个数的交换。
a=10;b=20;
做这题首先要知道:
位操作符
支持交换律
且num^num=0,0^num=num
那么我们就可以解决这道题
先来看代码实现,方便理解思路
代码实现:
#include <stdio.h>
int main()
{int a = 10;int b = 20;a = a^b;b = a^b;a = a^b;printf("a = %d b = %d\n", a, b);return 0;
}
思路:
将
a = a^b的a带入b = a^b中的a,即b=a^b^b,则b=10
b = a^b的b带入a =a^b中的b,即a=a^a^b,则a=20
一一一一一一一一一一一一一一分割线一一一一一一一一一一一一一一
整数转换
整数转换,链接奉上

思路:
首先我们要知道,
num & 1为最后一位二进制的数字,
那我们使用移位操作符遍历一下整数的32位比特位就迎刃而解
代码实现:
int convertInteger(int A, int B)
{int count=0;//创建计数器int i=0;for(i=0;i<32;i++){if((A>>i&1)!=(B>>i&1))count++;}return count;
}
一一一一一一一一一一一一一一分割线一一一一一一一一一一一一一一
二进制中1的个数
注意:此题无链接

这题和上一题大同小异,都可以使用
位移操作符与位操作符遍历解决,但这种方法必须循环32次(整形情况下)才能得到结果
还有一种方法:
使用
num&(num-1),这个式子的意义是什么呢?
是将式子最右边的1消掉
举个例子:
while(num)
{num&(num-1);
}
//假设在while循环中,设num为15,那么二进制就为11111111 num1110 num-11110 新的num1101 num-11100 新的num1011 num-11000 新的num0111 num-10000 新的num
可以看到,当
num为0时循环停止,循环了4次,也就是1的个数
我们就可以使用这种方法做题
思路:
使用
num&(num-1)计算二进制1的个数
代码实现:
#include <stdio.h>
int main()
{int num = -1;int i = 0;int count = 0;//计数while(num){count++;num = num&(num-1);}printf("二进制中1的个数 = %d\n",count);return 0;
}
一一一一一一一一一一一一一一分割线一一一一一一一一一一一一一一
不用加减乘除实现加法
不用加减乘除做加法,链接奉上

按位异或其实有个别名,叫做不进位加法,什么意思呢?
就是可以计算不进位的加法
例如:
int a=10;
//0000 1010
int b=20;
//0001 0100
int sum=a^b;
//0001 1110也就是30,
//我们发现当没有进位时,按位异或可以代替加法,那么有进位怎么办呢?
不过我们要想解决这个题,仅仅知道不进位加法是不够的,
我们从10进制举例
计算12+9:
1.
1+0=0,2+9=1(先不计算进位),结果为11
2.2+9有进位,进位为10
3.两者相加:10+11=21
既然如此,我们也可以利用这种方法计算,那进位如何表示呢?
二进制中只有两个1才会进位,因此我们按位与两个要相加的数,再进行左移就可以模拟进位。
思路:
1.将两个
要相加的数字按位异或
2.将两个数字进行按位与并向左移1位计算出进位
3.将两数相加,此时只需重复上述两个步骤,直到进位为0。
代码实现:
int Add(int num1, int num2 )
{int sum=0;int forward=0;do{sum=num1^num2;forward=(num1&num2)<<1;num1=sum;//num1与num2顺序不重要num2=forward;}while(forward);return sum;
}
一一一一一一一一一一一一一一分割线一一一一一一一一一一一一一一
寻找奇数
寻找奇数,链接奉上
思路:
在不创建临时变量交换整数,
我们了解了num^num=0,0^num=num,那我们这题就可以使用这种方法
#include <stdio.h>
#include<stdlib.h>int main()
{int n=0;scanf("%d",&n);int arr[n];//由编译器决定是否支持加长数组,//牛客网支持,也可以不使用加长数组//根据题目条件选择合适的个数范围int ans=0;for(int i=0;i<n;i++){scanf("%d",&arr[i]);ans^=arr[i];}printf("%d",ans);return 0;
}
一一一一一一一一一一一一一一分割线一一一一一一一一一一一一一一
错误的集合(必看)
错误的集合,链接奉上

思路:
我们发现,重复的数字与消失的数字出现的次数都是偶数次(2和0次),其他的数字出现次数是奇数次(1次),此时我们可以多添加一个从1~n正确的数字集合,使重复的数字与缺失的数字为奇数次(3和1次),其他的数字出现次数为偶数次(2次),我们利用异或就可以比较好的解决
设x,y分别为重复的数字与消失的数字,将2n个数字按位异或在一起,因为num^num=0,0^num=num,结果为x^y,我们记为xor
因为x!=y,故xor不为0,我们此时令lowbit=xor&(-xor),这是为了取得x与y最低位不同比特位(其实只要是不同的就可以,只是最低位好获得),简单的解释一下:
当x与y有最低位bit位不同时时,当前位异或的结果为1,那我们如何找到这个1呢
使用lowbit=xor&(-xor)
例如:
0000 101010的补码
1111 0110-10的补码
0000 0010按位与得到最低位不同比特位
得到lowbit后,将2n个数字分成两组,第一组每个数字a都满足a&lowbit==0,第二组每个数字b满足b&lowbit!=0
创建个2个变量,num1与num2,将第一组的a按位与在一起赋值给num1,另一组同样赋值给num2,此时num1与num2就是x或y,因为相同的数字肯定在一组,并且除了x与y出现的次数都是偶数次,故得到num1与num2就是x或y
此时将x与nums数组遍历比较一遍,如果出现即为消失的数字,否则相反。
代码实现:
int* findErrorNums(int* nums, int numsSize, int* returnSize)
{static int arr[2];int xor=0;for(int i=1;i<=numsSize;i++){xor^=nums[i-1];xor^=i;}//得到x^yint lowbit=xor&(-xor);//得到最低位比特位int num1=0;int num2=0;for(int i=0;i<numsSize;i++)//分组nums数组{if((nums[i]&lowbit)==0)num1^=nums[i];elsenum2^=nums[i];}for(int i=1;i<=numsSize;i++)//分组添加的数字{if((i&lowbit)==0)num1^=i;elsenum2^=i;}int count=0;//计数器int i=0;for(i=0;i<numsSize;i++){if(nums[i]==num1)count++;}if(count==0){arr[1]=num1;arr[0]=num2;}else{arr[1]=num2;arr[0]=num1;}*returnSize=2;return arr;
}小技巧:
一些位运算中的简便运算
1.
x & 1是奇数返回1,是偶数返回零,可以放在if中判断奇偶
2.x |= 1<<j等价于x += pow(2,j);
3.x<<2 x<<1,在十进制中表现的是乘上2的多少次方,在二进制中,就是先将这个x转换为二进制,然后整个数往前移位。(最后转化回去还是一样的)
4.num^num=0,0^num=num,异或也叫xor
总结:
在遇到数字重复时,二进制时,计算时,可能会有操作符的做法
遇到不会做的题很正常,不要感到沮丧,要知道我们也是站在巨人的肩膀上才能看得更远
相关文章:

【C语言】位操作符的一些题目与技巧
初学者在学完位操作符之后,总是不能很好的掌握,因此这篇文章旨在巩固对位操作符的理解与使用。 有的题目可能会比较难以接受,但是看完一定会有收获 目录 位操作符:一些题目:不创建临时变量交换整数整数转换二进制中1的…...
爬虫逆向实战(二十二)--某恩数据电影票房
一、数据接口分析 主页地址:某恩数据 1、抓包 通过抓包可以发现数据接口是API/GetData.ashx 2、判断是否有加密参数 请求参数是否加密? 无请求头是否加密? 无响应是否加密? 通过查看“响应”模块可以发现,响应是…...

火山引擎发布自研视频编解码芯片
2023年8月22日,火山引擎视频云宣布其自研的视频编解码芯片已成功出片。经验证,该芯片的视频压缩效率相比行业主流硬件编码器可提升30%以上,未来将服务于抖音、西瓜视频等视频业务,并将通过火山引擎视频云开放给企业客户。 火山引…...

投递技术类简历的注意事项
简历修改的背景 作为程序员,随着工作年限的增加,要定期的去修改自己的简历中的工作项目,一方面可以促进自己复盘一下工作成果和个人成长,另外也能给自己换工作提供一个前置的便捷性。 注意事项 修改简历的时候有哪些需要注意的…...
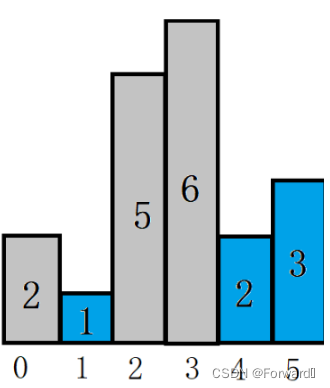
每日一题——柱状图中最大的矩形
柱状图中最大的矩形 题目链接 用什么数据结构? 要得到柱状图中最大的矩形,我们就必须要知道对于每一个高度heights[i],他所能勾勒出的矩形最大是多少(即宽度最大是多少)。 而对应到图上我们可以知道,要知…...

Banana Pi推出基于龙芯2K1000LA处理器的信创工业控制开发平台
Banana Pi推出基于龙芯2K1000LA处理器的信创工业控制开发平台:BPI-5202信创工业控制开发平台 BPI-5202 龙芯2K1000LA 信创工业控制开发平台 1.1 工控机的应用场景 物联网的狂潮,既是一场众多的计算机软硬件厂家(也包括通讯方案和产品厂家&…...
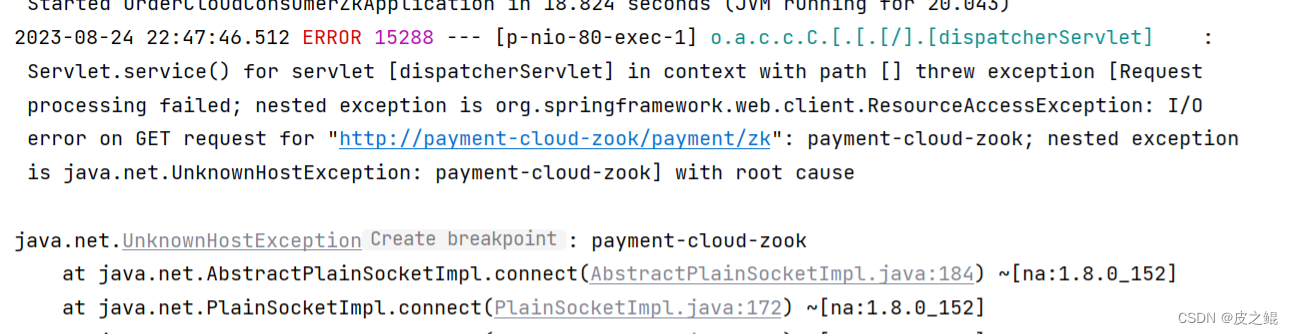
springCloud整合Zookeeper的时候调用找不到服务
SpringCloud整合Zookeeper的时候调用找不到服务 首先,我们在注册中心注册了这个服务: 然后我们使用RestTemplate 调用的时候发现失败了:找不到这个服务: 找了很多资料发现这个必须要加上负载才行 BeanLoadBalanced //负载publi…...

【kubernetes】使用kubepshere部署中间件服务
KubeSphere部署中间件服务 入门使用KubeSphere部署单机版MySQL、Redis、RabbitMQ 记录一下搭建过程 (内容学习于尚硅谷云原生课程) 环境准备 VMware虚拟机k8s集群,一主两从,master也作为工作节点;KubeSphere k8skubesphere devops比较占用磁…...

如何从tabbar页面传数据
无论是百度小程序还是微信小程序,app.json中规定的tabbar页面是不支持传参的,例如: <navigator url../service/service?typeid6 openType"switchTab"> 服务项目 </navigator> 上面的navigater跳转有个属性&#…...

软考高级系统架构设计师系列论文七十四:基于构件的软件开发
软考高级系统架构设计师系列论文七十四:基于构件的软件开发 一、构件相关知识点二、摘要三、正文四、总结一、构件相关知识点 软考高级系统架构设计师系列之:面向构件的软件设计,构件平台与典型架构...

图为科技_边缘计算在智能安防领域的作用
边缘计算在智能安防领域发挥着重要的作用。智能安防系统通常需要处理大量的图像、视频和传感器数据,并对其进行实时分析和处理。边缘计算可以将计算和数据处理功能移动到离数据源更接近的地方,例如摄像头、传感器设备或安防终端。 以下是边缘计算在智能…...
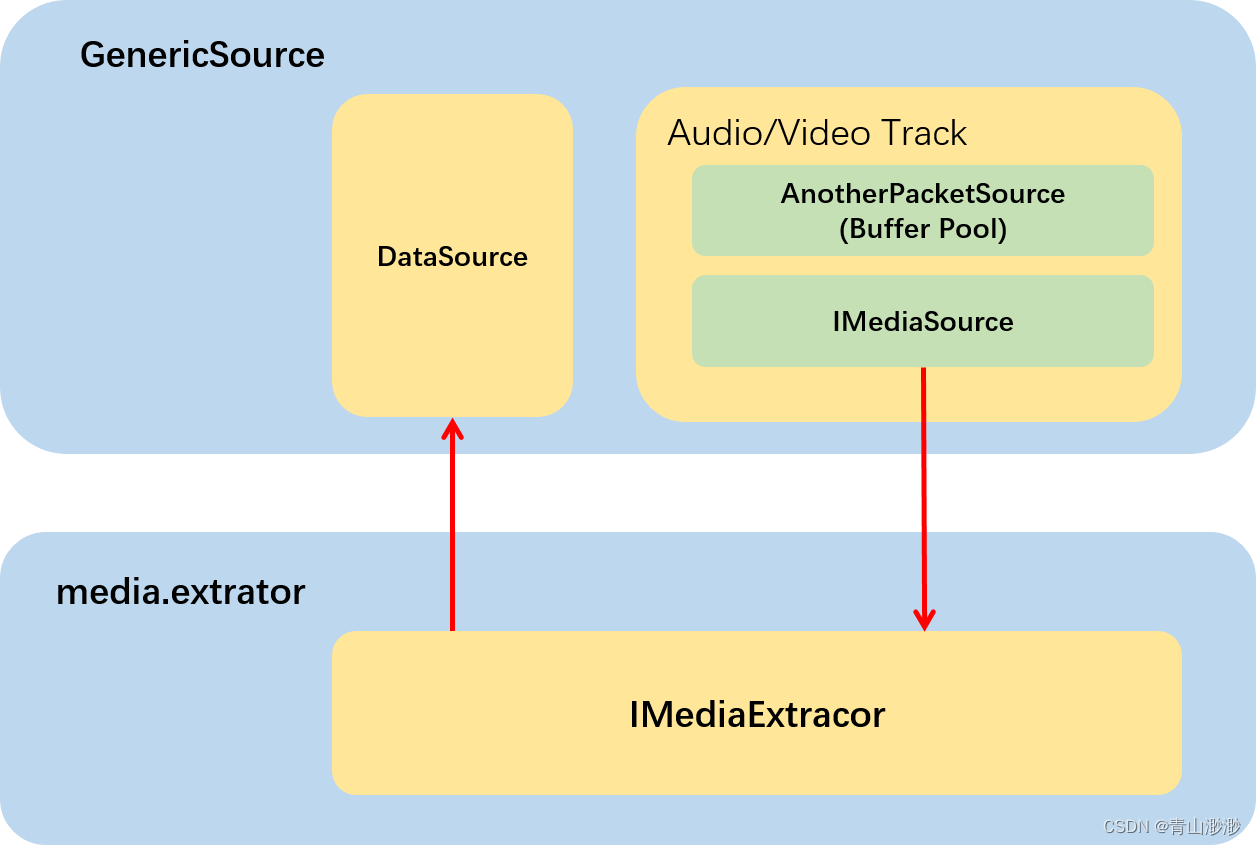
Android 13 - Media框架(7)- NuPlayer::Source
Source 在播放器中起着拉流(Streaming)和解复用(demux)的作用,Source 设计的好坏直接影响到播放器的基础功能,我们这一节将会了解 NuPlayer 中的通用 Source(GenericSource)关注本地…...
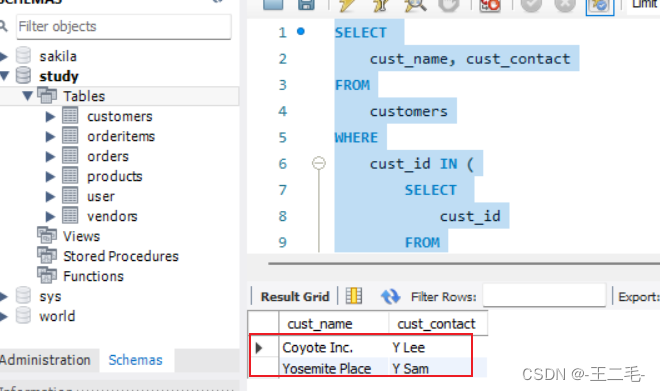
MySql015——使用子查询
一、创建customers表 ######################## # Create customers table ######################## use study;CREATE TABLE customers (cust_id int NOT NULL AUTO_INCREMENT,cust_name char(50) NOT NULL ,cust_address char(50) NULL ,cust_city char…...

leetcode 355 设计推特
用链表存储用户发送的每一个推特,用堆获取最先的10条动态 class Twitter {Map<Integer,Set<Integer>> followMap;//规定最新的放到最后Map<Integer,Tweet> postMap;//优先队列(堆)PriorityQueue<Tweet> priorityQueue;int time…...
倒数 2 周|期待 2023 Google开发者大会
9 月 6-7 日,中国上海 前沿科技,新知同享 趣味体验,灵感齐聚 技术生态,多元共进 关注官网最新信息,敬请期待大会开幕 2023 Google 开发者大会官网 相信你一定记得,在今年 5 月的 Google I/O 大会上&am…...

代码随想录day57
516最长回文子序列 class Solution { public:int longestPalindromeSubseq(string s) {vector<vector<int>>dp(s.size(),vector<int>(s.size(),0));for(int i0;i<s.size();i)dp[i][i]1;for(int is.size()-1;i>0;i--){for(int ji1;j<s.size();j){if…...

YOLOv5、v8改进:CrissCrossAttention注意力机制
目录 1.简介 2. yolov5添加方法: 2.1common.py构建CrissCrossAttention模块 2.2yolo.py中注册 CrissCrossAttention模块 2.3修改yaml文件。 1.简介 这是ICCV2019的用于语义分割的论文,可以说和CVPR2019的DANet遥相呼应。 和DANet一样,…...
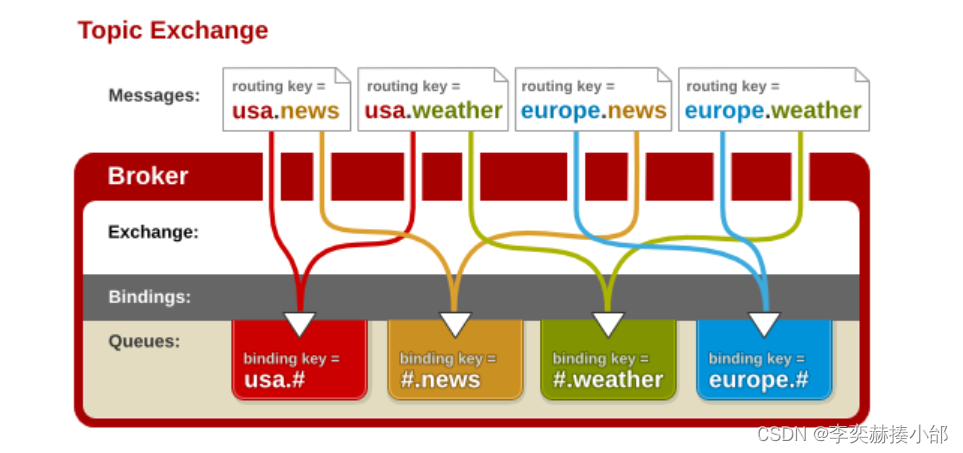
RabbitMQ特性介绍和使用案例
❤ 作者主页:李奕赫揍小邰的博客 ❀ 个人介绍:大家好,我是李奕赫!( ̄▽ ̄)~* 🍊 记得点赞、收藏、评论⭐️⭐️⭐️ 📣 认真学习!!!🎉🎉 文章目录 RabbitMQ特性…...
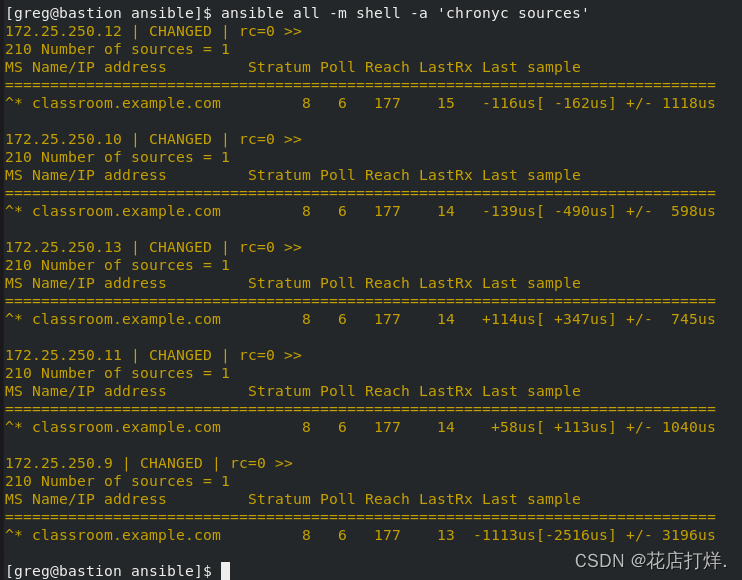
Ansible 使用 RHEL 系统角色
安装 RHEL 系统角色软件包,并创建符合以下条件的 playbook /home/greg/ansible/timesync.yml 在所有受管节点上运行 使用 timesync 角色 配置该角色,以使用当前有效的 NTP 提供商 配置该角色,以使用时间服务器 172.25.254.254 配置该角色&am…...

重新认识Android中的线程
线程的几种创建方式 new Thread:可复写Thread#run方法。也可以传递Runnable对象,更加灵活。缺点:缺乏统一管理,可能无限制新建线程,相互之间竞争,及可能占用过多系统的资源导致死机或oom。 new Thread(new…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
