计算机毕设 基于机器学习的餐厅销量预测 -大数据 python
文章目录
- 0 前言
- 餐厅销量预测
- 模型简介
- 2.ARIMA模型介绍
- 2.1自回归模型AR
- 2.2移动平均模型MA
- 2.3自回归移动平均模型ARMA
- 三、模型识别
- 四、模型检验
- 4.1半稳性检验
- (1)用途
- (1)什么是平稳序列?
- (2)检验平稳性
- ◆白噪声检验(纯随机性检验)
- (1)用途
- (1)什么是纯随机序列?
- (2)检验纯随机性
- 五、Python实战
- (一)导入工具及数据
- (二)原始序列的检验
- (三)一阶差分序列的检验
- (四)定阶(参数调优)
- (五)建模与预测
- 最后
0 前言
🔥 这两年开始毕业设计和毕业答辩的要求和难度不断提升,传统的毕设题目缺少创新和亮点,往往达不到毕业答辩的要求,这两年不断有学弟学妹告诉学长自己做的项目系统达不到老师的要求。
为了大家能够顺利以及最少的精力通过毕设,学长分享优质毕业设计项目,今天要分享的是
🚩 **基于机器学习的餐厅销量预测 **
🥇学长这里给一个题目综合评分(每项满分5分)
- 难度系数:3分
- 工作量:3分
- 创新点:3分
餐厅销量预测
模型简介
2.ARIMA模型介绍
2.1自回归模型AR
自回归模型描述当前值与历史值之间的关系,用变量自身的历史时间数据对自身进行预测。自回归模型必须满足平稳性的要求。
自回归模型首先需要确定一个阶数p,表示用几期的历史值来预测当前值。p阶自回归模型的公式定义为:
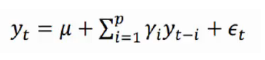
上式中yt是当前值,u是常数项,p是阶数
ri是自相关系数,et是误差。
自回归模型有很多的限制:
1、自回归模型是用自身的数据进行预测
2、时间序列数据必须具有平稳性
3、自回归只适用于预测与自身前期相关的现象
2.2移动平均模型MA
移动平均模型关注的是自回归模型中的误差项的累加 ,移动平均法能有效地消除预测中的随机波动,q阶自回归过程的公式定义如下:
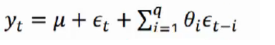
2.3自回归移动平均模型ARMA
自回归模型AR和移动平均模型MA模型相结合,我们就得到了自回归移动平均模型ARMA(p,q),计算公式如下:
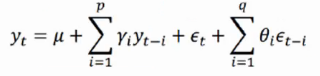
三、模型识别
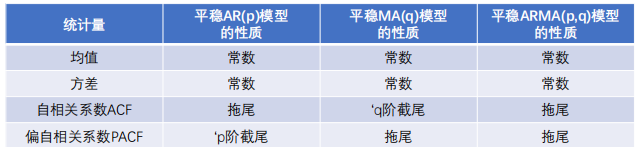
自相关函数ACF:时间序列观测值与其过去的观测值之间的线性相关性。
偏自相关函数PACF:在给定中间观测值的条件下,时间序列观测值预期过去的观测值之间的线性相关性
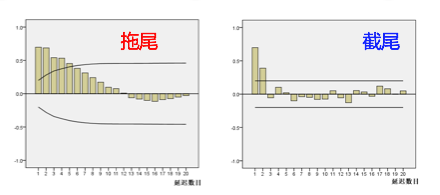
拖尾和截尾
拖尾指序列以指数率单调递减或震荡衰减,而截尾指序列从某个时点变得非常小:
四、模型检验
4.1半稳性检验
(1)用途
建模之前,检验时间序列数据是否满足平稳性,才能进-步建模
(1)什么是平稳序列?
如果时间序列在某-常数附件波动且波 动范围有限,数学表达即常数均值和常数方差,并且延迟k期的序列变量的自协方差和自相关系数是相等的,则称该序列为平稳序列。
(2)检验平稳性
方法一:图检验(偏主观)
时序图检验:在某-常数附近波动且波动范围有限。
自相关图检验:平稳序列具有短期相关性,但随着延迟期数k的增加,自相关系数会快速衰减趋向于零。
方法二:单位根检验
不存在单位根即是平稳序列。
◆白噪声检验(纯随机性检验)
(1)用途
建模之前,检验数据是否满足白噪声检验,非白噪声才能进一步建模。
建模后,检验残差是否满足白噪声检验,通过检验,建模才成立。
(1)什么是纯随机序列?
如果-个序例是纯随机序列,那么序列值之间没有任何关系,则自相关系数为零(理论)或接近于零(实际) .
(2)检验纯随机性
方法- -:图检验
自相关图检验:自相关系数为零或接近于零
QQ图检验:大部分点在直线上,则数据符合正态分布
方法二: D-W检验或L .B统计量检验
五、Python实战
(一)导入工具及数据
#导入数据
sale=pd.read_excel(“C://Python//分享资料2//arima_data.xls”)
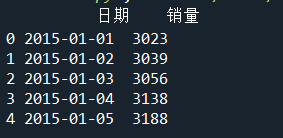
print(sale.head())
print(sale.info())
查看数据
共有37个整数型样本数据
(二)原始序列的检验
#时序图观看是否平稳序列
plt.figure(figsize=(10,5))
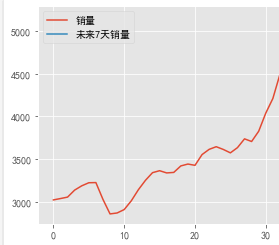
sale[‘销量’].plot()
plt.legend([‘销量’])
plt.show()
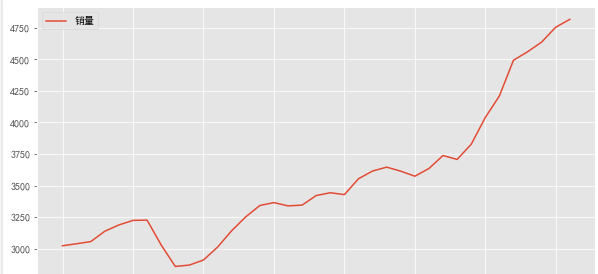
上图为一个单调递增的序列,说明数据是不平稳的。
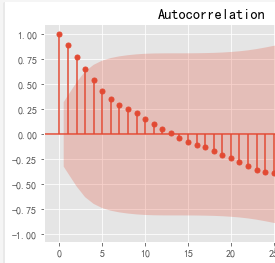
自相关图
# 查看自相关图
sale[‘销量’]=sale[‘销量’].astype(‘float’)
plot_acf(sale[‘销量’],lags=35).show()
#解读:自相关系数长期大于零,没有趋向于零,说明序列间具有很强的长期相关性。
平稳性检验
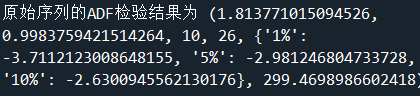
print(‘原始序列的ADF检验结果为’,ADF(sale[‘销量’]))
#解读:P值(第二个)大于显著性水平α(0.05),接受原假设(非平稳序列),说明原始序列是非平稳序列。
(三)一阶差分序列的检验
#方法:单位根检验
# print(‘原始序列的ADF检验结果为’,ADF(sale[‘销量’]))
d1_sale=sale.diff(periods=1, axis=0).dropna()
d1_sale=d1_sale['销量']
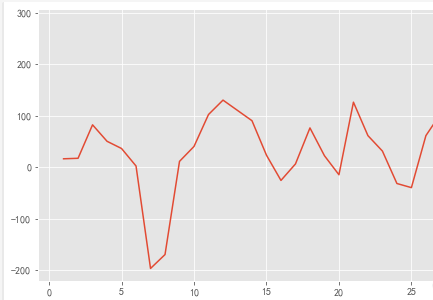
#时序图
plt.figure(figsize=(10,5))
d1_sale.plot()
plt.show()
#解读:在均值附件比较平稳波动#自相关图
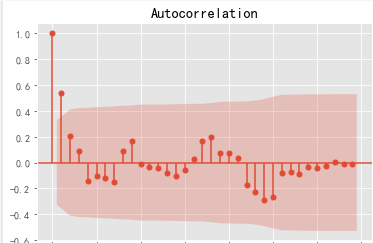
plot_acf(d1_sale,lags=34).show()
#解读:有短期相关性,但趋向于零。#平稳性检验
print('原始序列的ADF检验结果为:',ADF(d1_sale))#解读:P值小于显著性水平α(0.05),拒绝原假设(非平稳序列),说明一阶差分序列是平稳序列。

平稳性检验ADF小于0.05,说明一阶差分是平稳的
白噪声检验
print(‘一阶差分序列的白噪声检验结果为:’,acorr_ljungbox(d1_sale,lags=1))#返回统计量、P值
#解读:p值小于0.05,拒绝原假设(纯随机序列),说明一阶差分序列是非白噪声。

p值小于0.05,拒绝原假设(纯随机序列),说明一阶差分序列是非白噪声。
(四)定阶(参数调优)
确定P值和Q值
# 参数调优:BIC
# # 模型调优的方法:AIC和BIC
# # 值越小越好
# # 参数调优的方法非常多,用不同方法得出的结论可能不同
# from pandas.core.frame import DataFrame
# pmax=int(len(d1_sale)/10) #一般阶数不超过length/10
# qmax=int(len(d1_sale)/10) #一般阶数不超过length/10
# bic_matrix=[]
# for p in range(pmax+1):
# tmp=[]
# for q in range(qmax+1):
# try:
# tmp.append(ARIMA(sale,(p,1,q)).fit().bic)
# except:
# tmp.append(None)
# bic_matrix.append(tmp)
# p,q=DataFrame(bic_matrix).stack().idxmin() #最小值的索引
# print(‘用BIC方法得到最优的p值是%d,q值是%d’%(p,q))
# pmax=int(len(d1_sale)/10) #一般阶数不超过length/10
# qmax=int(len(d1_sale)/10) #一般阶数不超过length/10# aic_matrix=[]
# for p in range(pmax+1):
# tmp=[]
# for q in range(qmax+1):
# try:
# tmp.append(ARIMA(sale,(p,1,q)).fit().aic)
# except:
# tmp.append(None)
# aic_matrix.append(tmp)
# aic_matrix=pd.DataFrame(aic_matrix)
# p,q=aic_matrix.stack().idxmin() #最小值的索引
# print('用AIC方法得到最优的p值是%d,q值是%d'%(p,q))
用AIC和BIC方法得到的最优的P值和Q值为0,1
(五)建模与预测
#构建模型
model=ARIMA(sale[‘销量’],(0,1,1)).fit()
#查看模型报告
print(model.summary2())
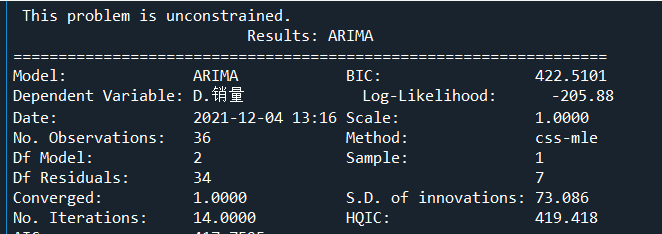
残差检验
#残差检验
#自相关图
resid=model.resid
plot_acf(resid,lags=35).show()
#解读:有短期相关性,但趋向于零。#偏自相关图
plot_pacf(resid,lags=20).show()#偏自相关图
plot_pacf(resid,lags=35).show()
#
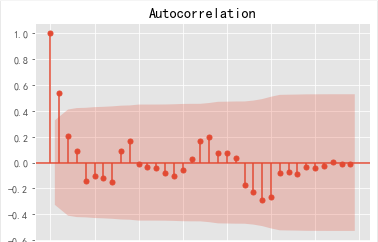
如图所示一阶,二阶,三阶都是非常小的数,说明它们之间的相关性比较小,可能是一个纯随机序列
#qq图:线性即正态分布
qqplot(resid, line=‘q’, fit=True).show()
#解读:残差服从正态分布,均值为零,方差为常数
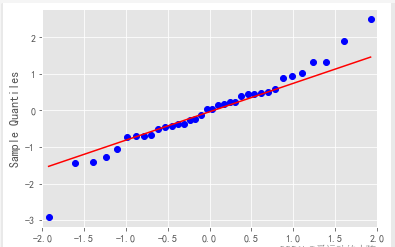
上图可以看出数据均匀的落在直线的周围,说明数据服从正态分布:均值为0,方差为常数,是一个纯随机序列。
预测
print(‘未来七天的销量数据:\n’)
print(model.forecast(7))
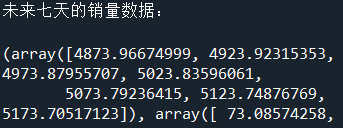
#预测
# print(‘未来七天的销量数据:\n’)
# print(model.forecast(7))
forecast=pd.Series(model.forecast(7)[0],index=pd.date_range(‘2015-2-7’,periods=7,freq=‘D’))
data=pd.concat((sale,forecast),axis=0)
data.columns=[‘日期’,‘销量’,‘未来7天销量’]
plt.figure(figsize=(10,5))
data[[‘销量’,‘未来7天销量’]].plot()
plt.show()
最后
相关文章:

计算机毕设 基于机器学习的餐厅销量预测 -大数据 python
文章目录 0 前言餐厅销量预测模型简介2.ARIMA模型介绍2.1自回归模型AR2.2移动平均模型MA2.3自回归移动平均模型ARMA 三、模型识别四、模型检验4.1半稳性检验(1)用途(1)什么是平稳序列?(2)检验平稳性 ◆白噪声检验(纯随机性检验)(1)用途(1)什么是纯随机序列?(2)检验纯随机性 五…...

layui 多选限制选择3个
可以使用 layui 的表单组件进行多选,然后通过 JavaScript 代码限制用户最多只能选择 3 个选项。具体的实现步骤如下: 在 layui 的表单组件中,使用多选框进行多选。 <div class"layui-form-item"><label class"layu…...

PyQt PySide6 QMessageBox使用教程
PySide6 是一个 Python 绑定到 Qt6 库的库,允许你在 Python 中创建 Qt6 应用程序。QMessageBox 是一个提供模式对话框,用于显示消息、询问问题或获取简单的输入的类。 以下是使用 PySide6 中的 QMessageBox 的基本方式: 导入必要的模块: f…...

Visual Studio软件安装包分享(附安装教程)
目录 一、软件简介 二、软件下载 一、软件简介 Visual Studio是微软公司开发的一款集成开发环境(IDE),广泛应用于Windows平台上的应用程序和Web应用程序的开发。以下是Visual Studio软件的主要特点和功能: 集成开发环境&#x…...

VB电脑销售系统设计与实现
前 言 本文论述了销售管理系统的开发过程,它包括了软件的开发环境,开发工具以及相关技术、系统分析、系统设计、实现等内容。 本系统能为企业繁重的工作带来极大的方便,提高了工作效率及工作准确性,能准确无误地查找货物的综合信息,为企业减少了许多工作细节。 为了使此…...

如何访问MySQL错误日志
通常情况下,MySQL中出现减速、崩溃或其他意外行为的根本原因可以通过分析错误日志来确定。在Ubuntu系统中,MySQL的默认位置是/var/log/mysql/error.log。在许多情况下,使用less程序最容易读取错误日志,这是一个命令行实用程序&…...
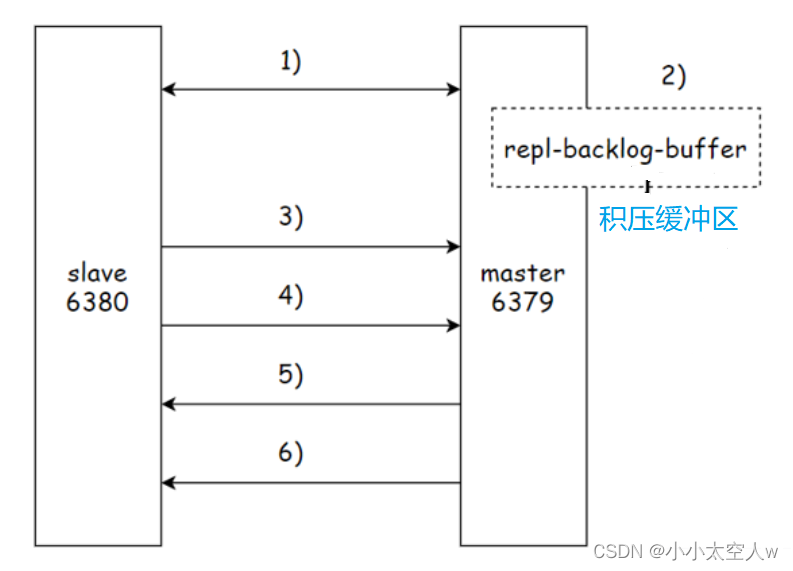
redis主从复制详解
目录 前言: 分布式系统 主从模式 主从同步连接过程 replication id作用 offset作用 psync命令(psync replicationId offset) 全量复制 全量复制过程 部分复制 部分复制过程 实时复制 前言: redis为了保证高可用,它支持…...

kubernetes/k8s驱逐机制总结篇
概述 k8s的驱逐机制是指在某些场景下,如node节点notReady、node节点压力较大等,将pod从某个node节点驱逐掉,让pod的上层控制器重新创建出新的pod来重新调度到其他node节点。这里也将kube-scheduler的抢占调度纳入到了驱逐的讨论范围内&#…...
Git gui教程---第七篇 Git gui的使用 返回上一次提交
1. 查看历史,打开gitk程序 2. 选中需要返回的版本,右键,然后点击Rest master branch to here 3.出现弹窗 每个选项我们都试一下,从Hard开始 返回的选项 HardMixedSoft Hard 会丢失所有的修改【此处的…...
Web 开发 Django 管理工具
上次为大家介绍了 Django 的模型,通过模型就可以操作数据库,从而就可以改变页面的展示内容,那问题来了,我们只能通过手动编辑模型文件来配置模型吗?当然不是,Django 为我们提供了强大的工具,可以…...

分类算法的评价指标
分类算法的评价指标 查准率、查全率、准确率、F1分数: 查准率(Precision): 模型预测为正例的样本中实际未正的比例。它关注的点在:预测为正例样本的准确性。 查全率(recall): 模型…...

智能工厂移动式作业轻薄加固三防平板数据采集终端
在这个高度自动化和数字化的环境中,数据采集变得尤为重要。为了满足这个需求,工业三防平板数据采集终端应运而生。工业三防平板数据采集终端采用了轻量级高强度镁合金材质,这使得它在保持轻薄的同时具有更强的坚固性。这种材质还具有耐磨防损…...

Python Flask token身份认证
首先安装依赖: pip install flask-jwt-extended 然后在主应用中(项目入口文件)加入以下代码: from flask import Flask from flask_jwt_extended import JWTManager #引入依赖 app Flask(__name__) app.config[JWT_SECRET_KEY…...

docker安装rabbitMQ
目录 1、拉取镜像 2、构造镜像 3、开启插件 4、开启安全组 5、访问 ui界面访问不到解决步骤 1、拉取镜像 docker pull rabbitmq 这里拉取的是最新镜像,若要指定版本可在后加上版本号即可;比如 docker pull rabbitmq:3.7.14 2、构造镜像 方式一:交…...
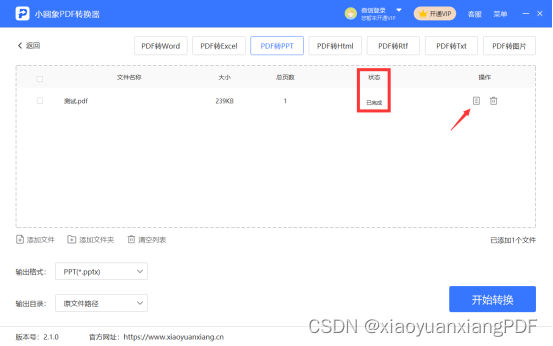
PDF如何转ppt?PDF转ppt的方法
PDF是一种广泛应用于文档传输和存储的格式,然而,在某些情况下,我们可能需要将PDF文件转换为PPT,以便更加灵活地编辑和展示内容。那么,PDF如何转ppt呢?在本文中,我们将介绍几种常用的方法和工具,…...
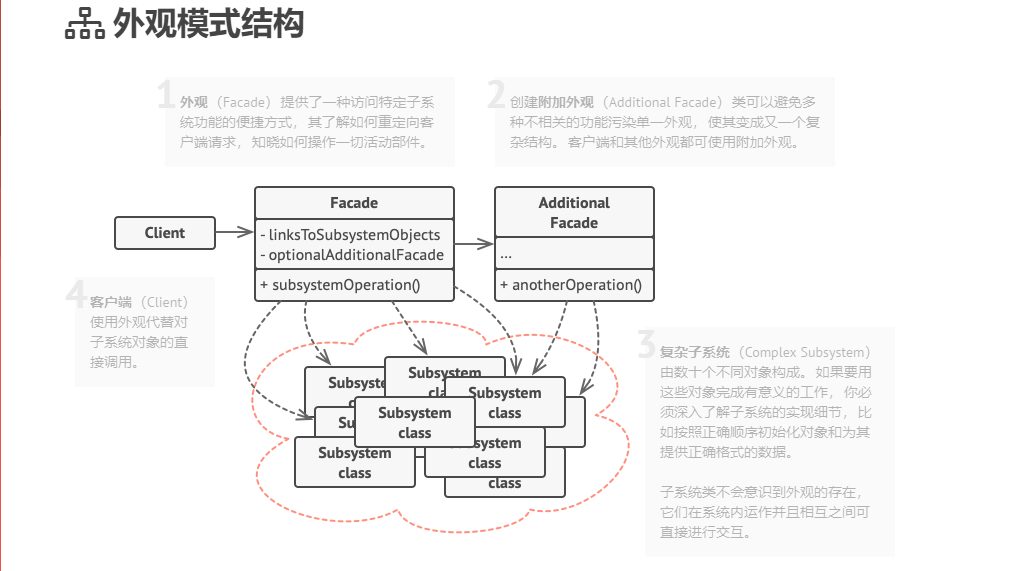
设计模式(8)外观模式
一、 1、使用背景:降低访问复杂系统的内部子系统时的复杂度,简化客户端之间的接口。 2、定义: 为子系统中的一组接口定义一个一致的界面,此模式定义了一个高层接口,这个接口使得这一子系统更加容易使用。完美地体现…...
Django(7)-项目实战-发布会管理
登录功能 模板页面 sign/templates/index.html <!DOCTYPE html> <html> <head><title>Login Page</title> </head> <body><h1>发布会管理</h1><form action"/login/" method"post"><la…...

Hbase-技术文档-java.net.UnknownHostException: 不知道这样的主机。 (e64682f1b276)
问题描述: 在使用spring-boot操作habse的时候,在对habse进行操作的时候出现这个问题。。 报错信息如下: 第一段报错: 第二段报错: java.net.UnknownHostException: e64682f1b276 问题定位解读: 错误 ja…...

OpenCV + CLion在windows环境下使用CMake编译, 出现Mutex相关的错误的解决办法
最近在windows下面用cmake编译OpenCV的项目代码,但是一直碰到找不到mutex的问题,百思不得其解, Executing task: g -g -o bin/debug.exe src/main.cppC:\MinGW\lib\opencv\build\include/opencv2/core/utility.hpp:697:14: error: recursive_mutex in namespace st…...
华为质量管理:从产品质量到用户体验,Kano模型成为新方向
目录 前言 华为质量管理的四个阶段 基于 IPD 如何做质量管理呢? CSDN相关课程 作者简介 前言 今天继续来谈谈华为流程体系中的质量管理过程。 通常来说质量具体是指产品的质量,也就是产品的使用价值及其属性。 产品再细分的话可以分为三个层次&a…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...
