【图论】拓扑排序
一.定义
![]()
拓扑排序是一种对有向无环图(DAG)进行排序的算法,使得图中的每个顶点在排序中都位于其依赖的顶点之后。它通常用于表示一些任务之间的依赖关系,例如在一个项目中,某些任务必须在其他任务之前完成。
拓扑排序的步骤如下:
-
找到入度为0的顶点:入度是指指向某个顶点的边的数量。首先,找到图中入度为0的顶点,它们是没有依赖关系的顶点,可以作为排序的起点。
-
将入度为0的顶点移出图:选择一个入度为0的顶点,将其从图中移除,并将与之相邻的顶点的入度减1。
-
重复步骤1和步骤2:重复上述步骤,直到所有顶点都被移除。如果图是有向无环图,那么拓扑排序会成功完成。
拓扑排序并不是对所有图都适用,只有在有向无环图中才有意义,因为循环依赖会导致拓扑排序无法进行。
二.例题
B3644 【模板】拓扑排序 / 家谱树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
三.思路
找出入度为0的点,即为最小辈分的,输出即可,然后取消它的所有连边。
eg:
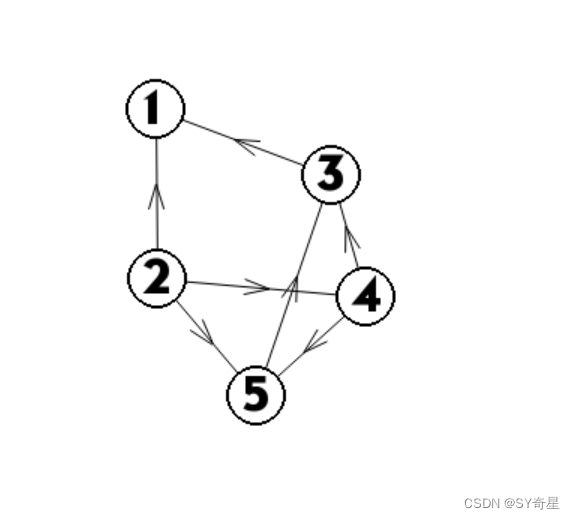
可知2无入度,说明2的辈分最小,输出并删除它的连边,print(2)

这时4无入度,print(2,4)
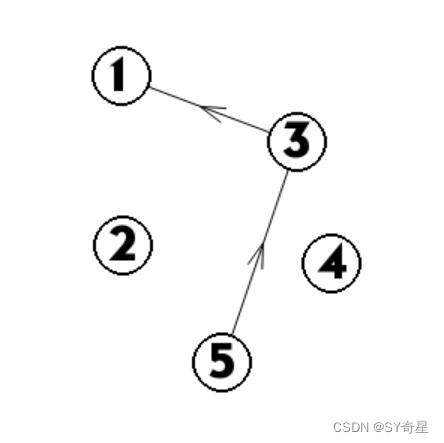
一直重复,print(2,4,5,3,1)
四.参考代码
#include<bits/stdc++.h>
using namespace std;
vector<int>to[101];
int in[101];
queue<int>q;
int main(){int n;scanf("%d",&n);for(int i=1;i<=n;i++){int x;while(scanf("%d",&x) && x!=0){to[i].push_back(x);in[x]++;}}for(int i=1;i<=n;i++){if(!in[i]) q.push(i);}while(!q.empty()){int x=q.front();q.pop();cout<<x<<" ";for(int i=0;i<to[x].size();i++){int y=to[x][i];in[y]--;if(!in[y]) q.push(y);}}return 0;
}
五.拓扑+dp
P1807 最长路 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
六.思路
不就是最长路吗?Dijkstra直接秒杀。
但还有什么更快的算法吗?
注意:这是有向无环图(DAG),是不是拓扑排序更快呢?拓扑排序就可以找到图的所有直径,然后DP即可。最后输出dp[n];
状态转移方程为:dp[v]=max(dp[v],dp[u]+w);
若dp[n]<0,那就说明没有边可以到达n点
七.参考代码
#include<bits/stdc++.h>
#define maxn 1505
using namespace std;
int n,m;
vector<int> to[maxn],wt[maxn];
int in[maxn],dp[maxn];
queue<int> q;
int main(){scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){int u,v,w;scanf("%d%d%d",&u,&v,&w);to[u].push_back(v);wt[u].push_back(w);in[v]++; }for(int i=1;i<=n;i++){dp[i]=-1e9;if(in[i]==0) q.push(i) ;}dp[1]=0;while(!q.empty()){int x=q.front(); q.pop();for(int i=0;i<to[x].size();i++){int y=to[x][i],w=wt[x][i];dp[y]=max(dp[y],dp[x]+w);in[y]--;if(!in[y]) q.push(y);}}if(dp[n]<0) cout<<-1;else cout<<dp[n];return 0;
}
相关文章:

【图论】拓扑排序
一.定义 拓扑排序是一种对有向无环图(DAG)进行排序的算法,使得图中的每个顶点在排序中都位于其依赖的顶点之后。它通常用于表示一些任务之间的依赖关系,例如在一个项目中,某些任务必须在其他任务之前完成。 拓扑排序的…...
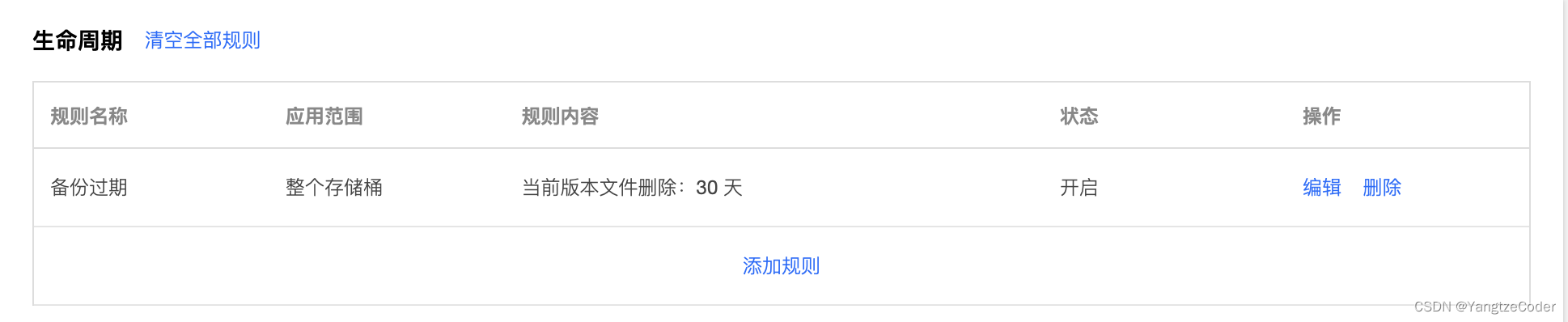
自动化备份方案
背景说明 网上有很多教程,写的都是从零搭建一个什么什么,基本上都是从无到有的教程,但是,很少有文章提及搭建好之后如何备份,这次通过请教GitHub Copilot Chat,生成几个备份脚本,以备后用。 注…...
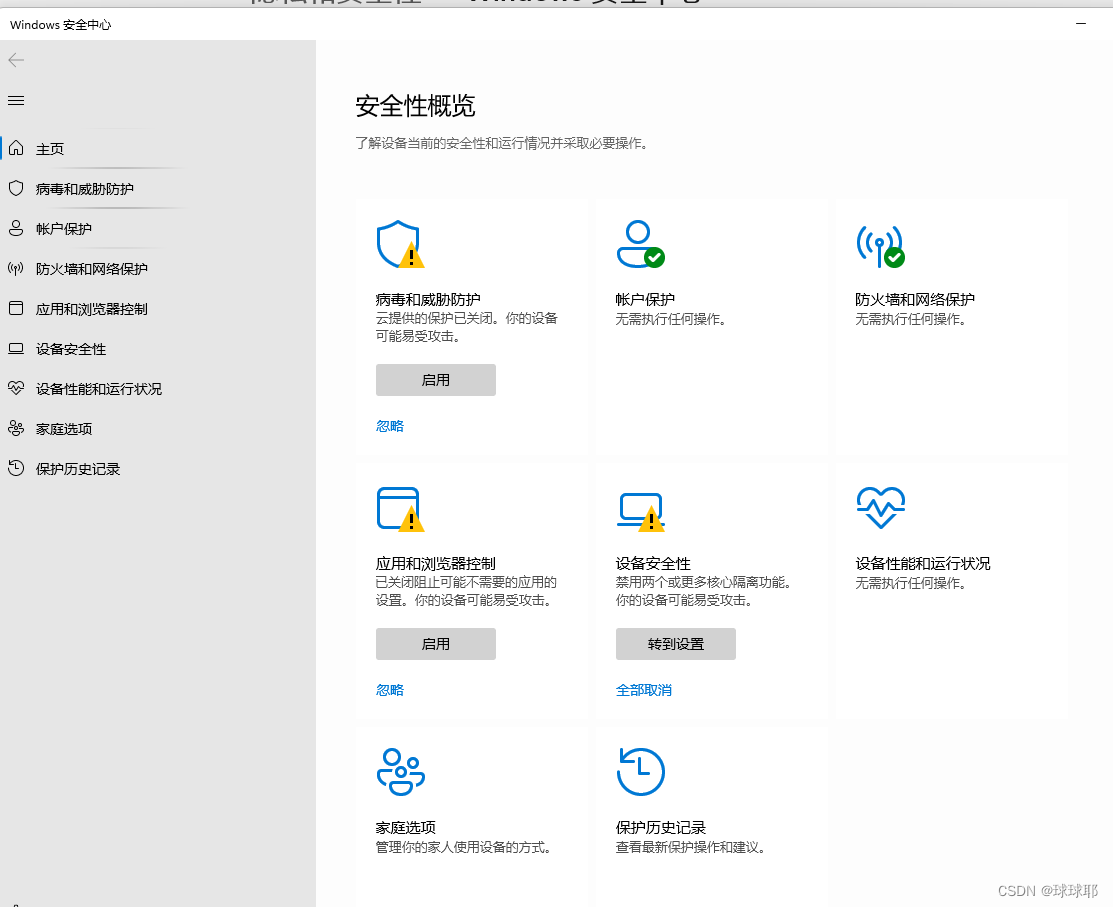
win11出现安全中心空白和IT管理员已限制对此应用的某些区域的访问
问题 windows安全中心服务被禁用 winr 输入services.msc 找到windows安全中心服务查看是否被禁用,改为启动,不可以改动看第三条 打开设置,找到应用—windows安全中心–终止–修复–重置 重启如果还是不行看第四条 家庭版系统需要打开gped…...

github实用指令(实验室打工人入门必备)
博主进入实验室啦,作为一只手残党决定在这里分享一些常用的github使用情景和操作指南来解救其他手残党。 内容随着情景增加实时更新。如果只有没几个内容说明场景不多(相信对手残党而言是再好不过的消息) 情景一:…...
6. 激活层
6.1 非线性激活 ① inplace为原地替换,若为True,则变量的值被替换。若为False,则会创建一个新变量,将函数处理后的值赋值给新变量,原始变量的值没有修改。 import torch from torch import nn from torch.nn import …...
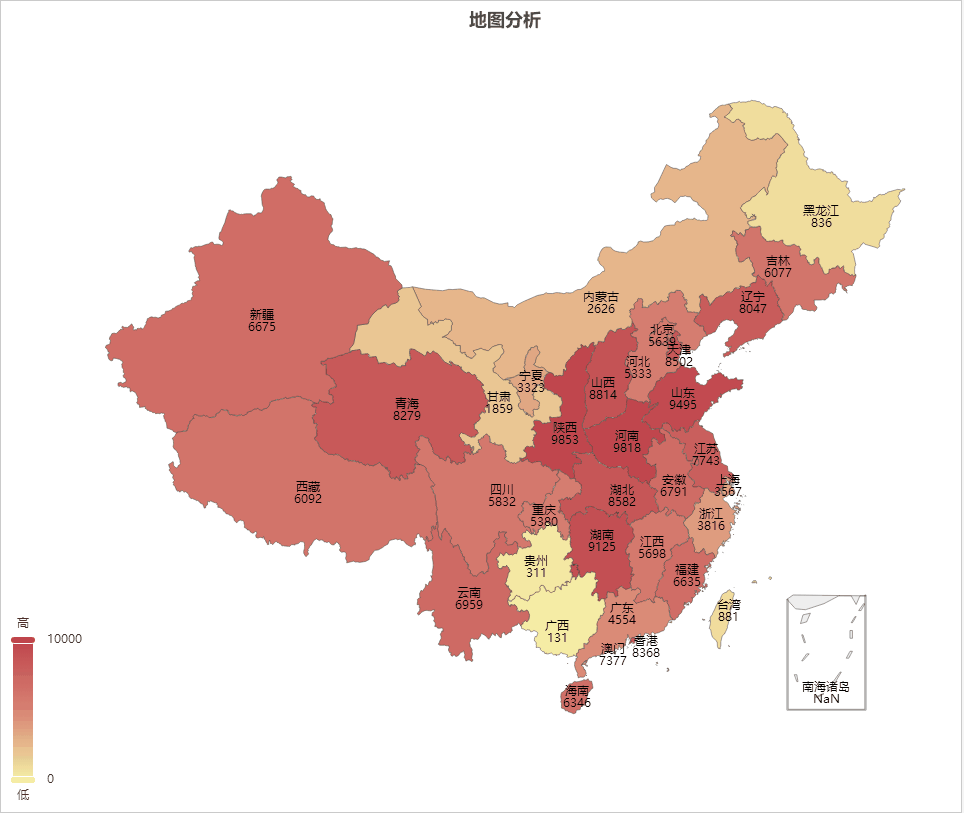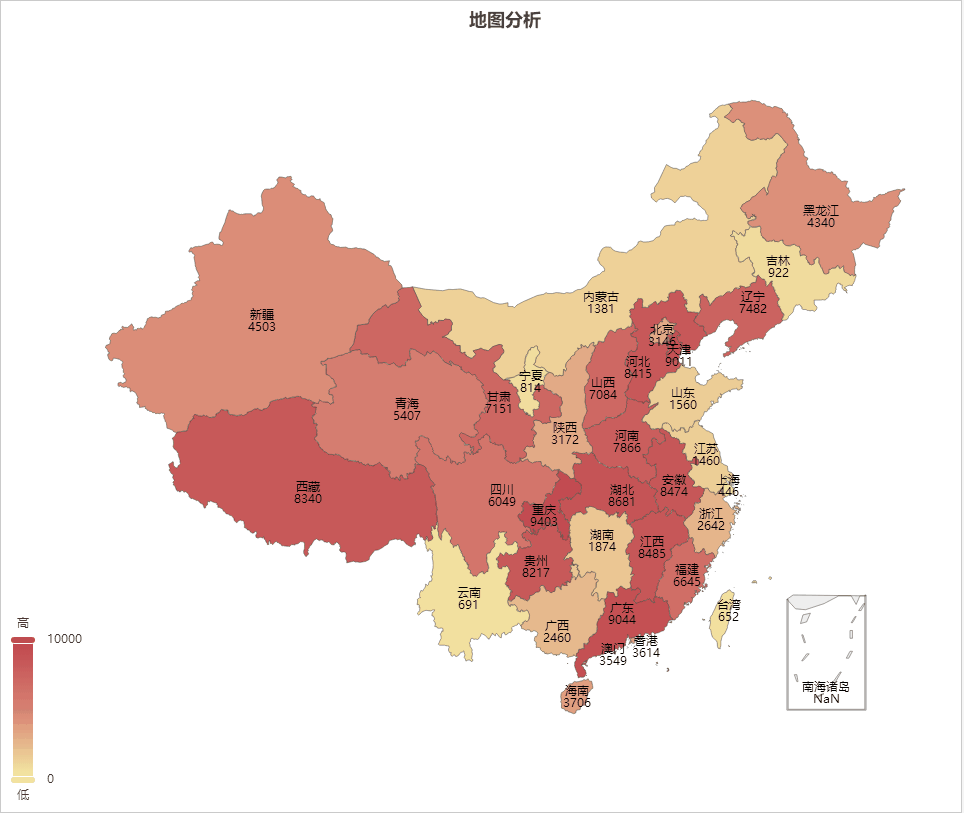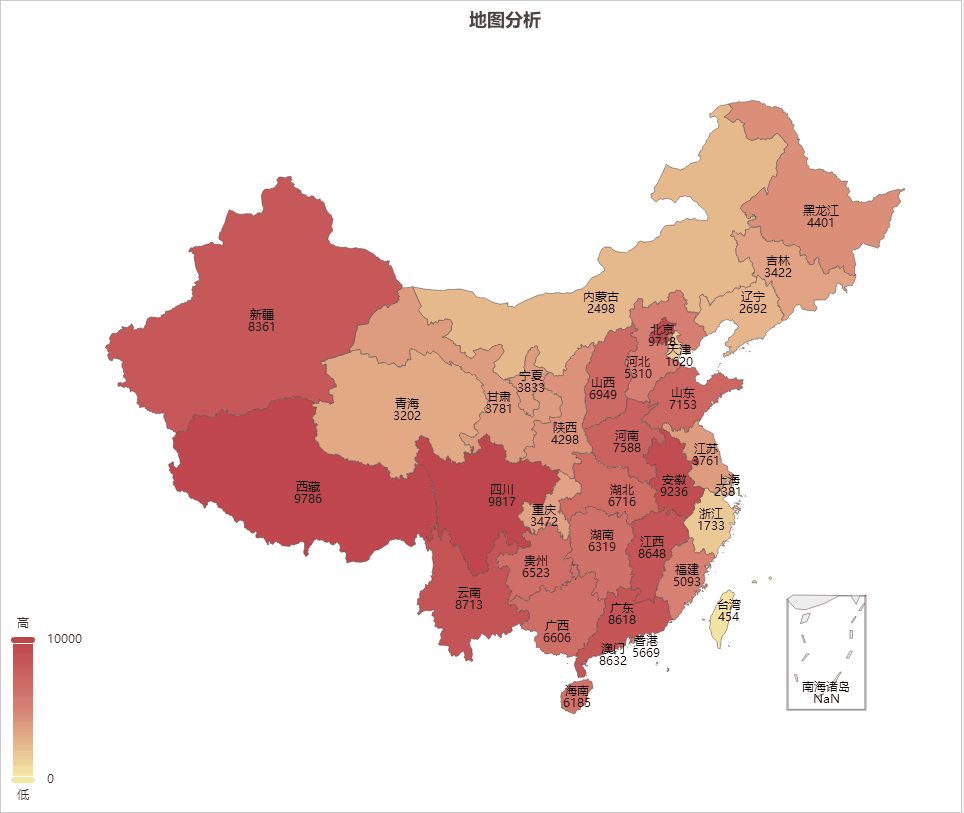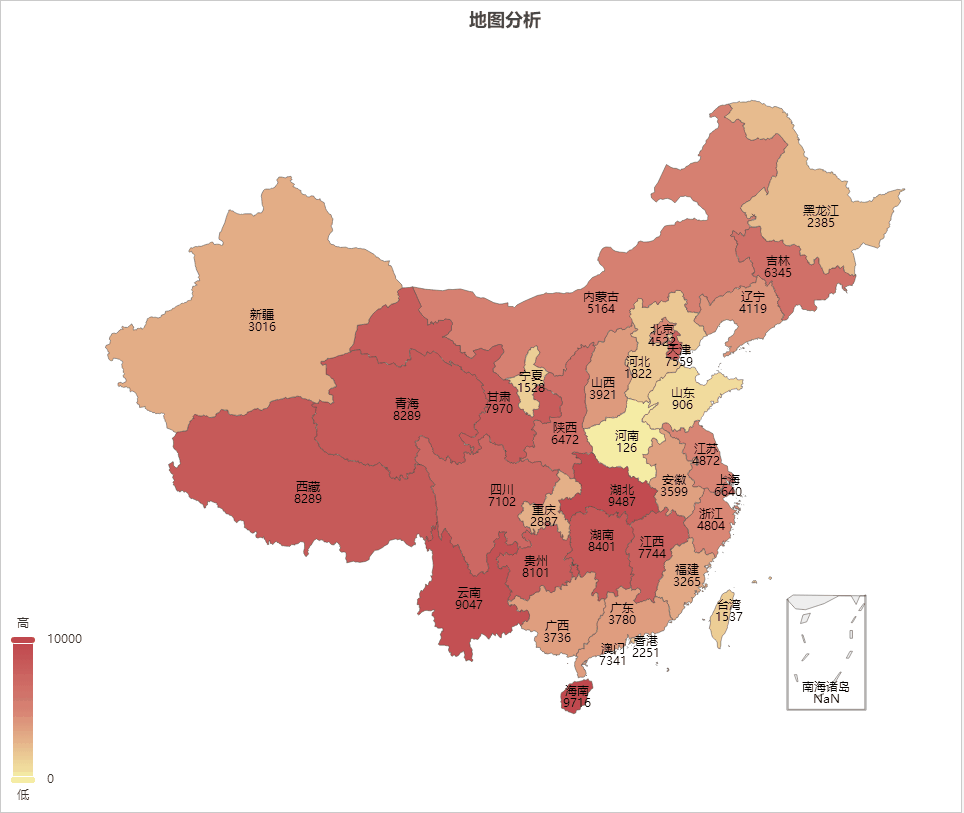
AIGC ChatGPT 制作地图可视化分析
地图可视化分析是一种将数据通过地图的形式进行展示的方法,可以让人们更加直观、快速、准确的理解和分析数据。以下是地图可视化分析的一些主要好处: 加强数据理解:地图可视化可以将抽象的数字转化为直观的图形,帮助我们更好地理解复杂的数据集。 揭示地理模式:地理位置是…...
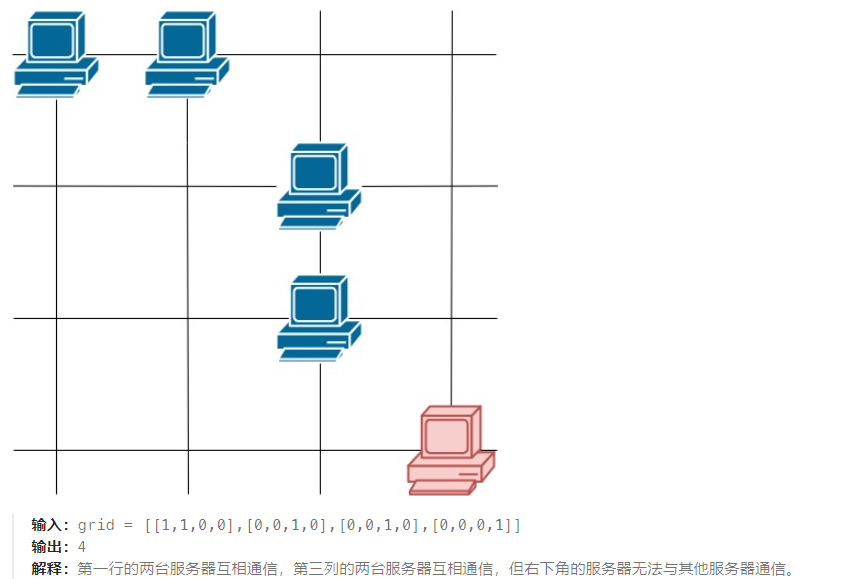
2023-08-24 LeetCode每日一题(统计参与通信的服务器)
2023-08-24每日一题 一、题目编号 1267. 统计参与通信的服务器二、题目链接 点击跳转到题目位置 三、题目描述 这里有一幅服务器分布图,服务器的位置标识在 m * n 的整数矩阵网格 grid 中,1 表示单元格上有服务器,0 表示没有。 如果两台…...

前端实习day35
今天是下早班的一天,下完班直接赶车回广州了,吐槽一下深圳站管理得真得差,候车厅小,人巨多,而且进站口的标识也很少,绕了好久才找到!下次再也不去了。 今天是改bug的一天,但是有半天…...

Linux安装jupyter notebook
1. Linux安装jupyter notebook 1.1 生成配置文件 这里在conda环境中安装。 jupyter notebook --generate-config --allow-root上面命令是生成配置文件,并且允许使用root用户运行。配置文件默认生成到~/.jupyter/jupyter_notebook_config.py。 具体解释如下&…...

【猿灰灰赠书活动 - 03期】- 【RHCSA/RHCE 红帽Linux认证学习指南(第7版) EX200 EX300】
说明:博文为大家争取福利,与清华大学出版社合作进行送书活动 图书:《RHCSA/RHCE 红帽Linux认证学习指南(第7版) EX200 & EX300》 一、好书推荐 图书介绍 《RHCSA/RHCE 红帽Linux认证学习指南(第7版) EX200 & E…...

当 Tubi 遇到 Ruby
有人说 Tubi 作为 RubyConf China 金牌赞助商,明明用极具吸引力的 Elixir 后端工程师岗位和高品质的 Elixir Meetup,“拐走了”一批又一批 Rubyist 投身于 Elixir 开发中,却依然让人想在 Tubi 展台前多停留一会儿。 为什么工程师、校友甚至 …...
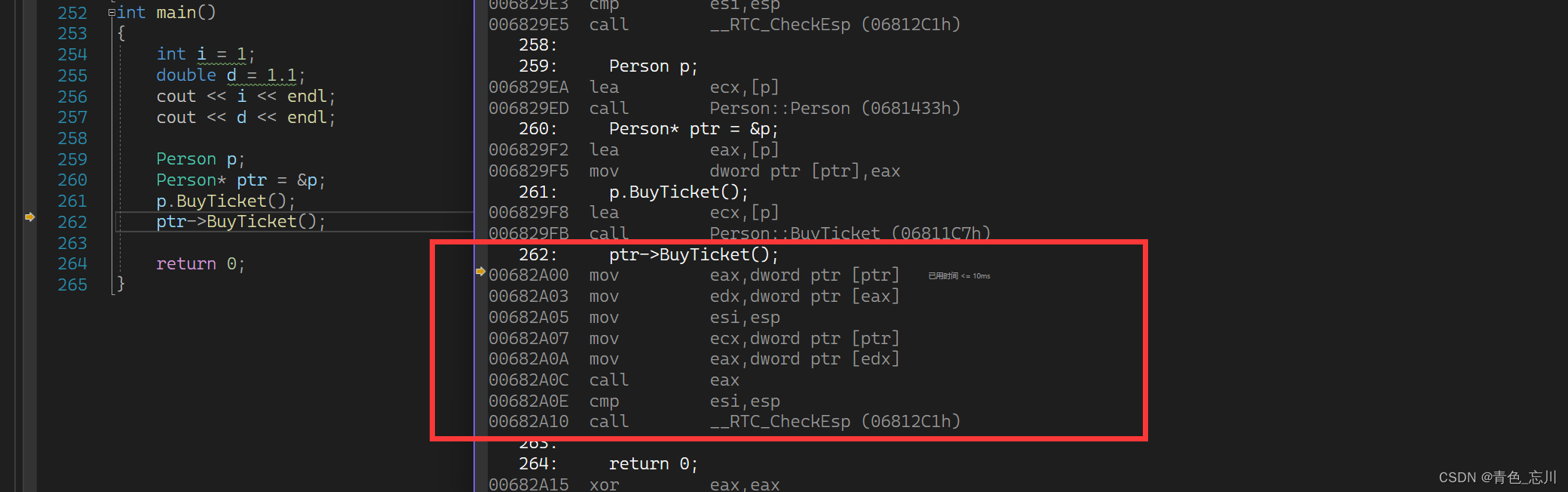
【C++从0到王者】第二十四站:多态的底层原理
文章目录 前言一、虚函数表二、一道经典的例题三、深度剖析多态的条件之一:为什么必须是父类的指针或引用四、深度剖析多态的条件之二:为什么是虚函数的重写/覆盖?五、虚函数表的一些总结六、关于Func3的验证七、动态绑定与静态绑定八、总结 …...

Java从入门到精通24==》数据库、SQL基本语句、DDL语句
Java从入门到精通24》数据库、SQL基本语句、DDL语句 2023.8.27 文章目录 <center>Java从入门到精通24》数据库、SQL基本语句、DDL语句一、什么是数据库二、数据库的优缺点1、使用数据库的优点:2、使用数据库的缺点: 三、MySQL基本语句四、DDL语句 …...
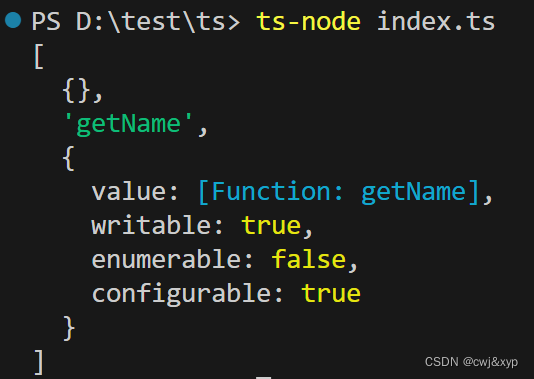
学习ts(十)装饰器
定义 装饰器是一种特殊类型的声明,它能够被附加到类声明,方法,访问符,属性或参数上,是一种在不改变原类和使用继承的情况下,动态的扩展对象功能。 装饰器使用expression形式,其中expression必须…...
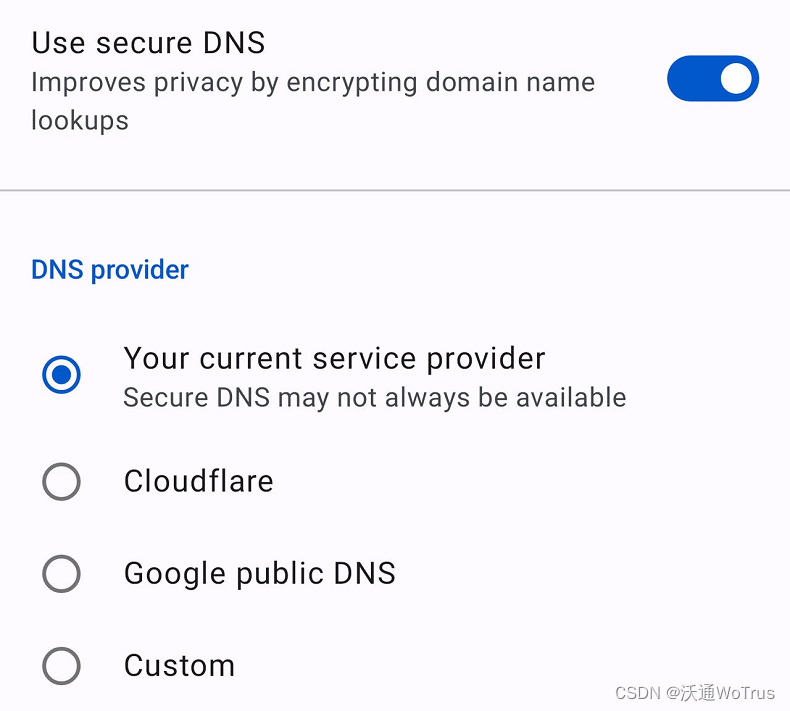
如何在 Opera 中启用DNS over HTTPS
DNS over HTTPS(基于HTTPS的DNS)是一种更安全的浏览方式,但大多数 Web 浏览器默认情况下不启用它。了解如何在 Opera 浏览器中启用该功能。 您可能不知道这一点,但您的网络浏览器并不像您希望的那样私密或安全。您会看到ÿ…...

STM32 F103C8T6学习笔记13:IIC通信—AHT10温湿度传感器模块
今日学习一下这款AHT10 温湿度传感器模块,给我的OLED手环添加上测温湿度的功能。 文章提供源码、测试工程下载、测试效果图。 目录 AHT10温湿度传感器: 特性: 连接方式: 适用场所范围: 程序设计: 设…...

QT基础使用:组件和代码关联(信号和槽)
自动关联 ui文件在设计环境下,能看到的组件可以使用鼠标右键选择“转到槽”就是开始组件和动作关联。 在自动关联这个过程中软件自动动作的部分 需要对前面头文件进行保存,才能使得声明的函数能够使用。为了方便,自动关联时先对所有文件…...
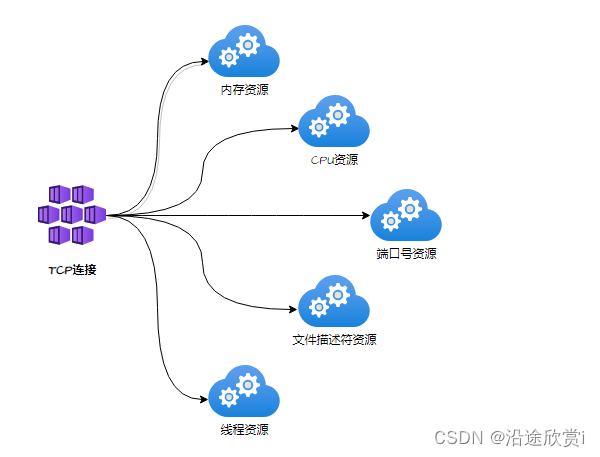
TCP最大连接数问题总结
最大TCP连接数量限制有:可用端口号数量、文件描述符数量、线程、内存、CPU等。每个TCP连接都需要以下资源,如图所示: 1、可用端口号限制 Q:一台主机可以有多少端口号?端口号与TCP连接?是否能修改&#x…...

【Docker】云原生利用Docker确保环境安全、部署的安全性、安全问题的主要表现和新兴技术产生
前言 Docker 是一个开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个可移植的容器中,然后发布到任何流行的Linux或Windows操作系统的机器上,也可以实现虚拟化,容器是完全使用沙箱机制,相互之间不会有任何接口。 云原生利用Docker确保环境安全、部署的…...

explain各个字段代表的意思
id:联表查询是每个表的读取顺序,数字越大越先被读取。相同就需要通过table字段判断select_type:查询类型或者是其他操作类型(PRIMARY、UNION、UNION RESULT等)table:正在访问哪个表partitions:匹…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...
