WPF基础入门-Class5-WPF命令
WPF基础入门
Class5-WPF命令
1、xaml编写一个button,Command绑定一个命令
<Grid><ButtonWidth="100"Height="40" Command="{Binding ShowCommand}"></Button>
</Grid>
2、编写一个model.cs
namespace WPF_Learn.Model
{class model_csdn{public model_csdn(){ShowCommand = new MyCommamd(show);}//注册命令,名字和xaml中一致public MyCommamd ShowCommand { get; set; } public void show(){MessageBox.Show("Show Message");}}
}
3、页面的cs文件绑定数据
public WPF_Form(){InitializeComponent();// 找到数据源 数据上下文this.DataContext = new WPF_Learn.Model.model_csdn();}
点击页面按钮:

相关文章:

WPF基础入门-Class5-WPF命令
WPF基础入门 Class5-WPF命令 1、xaml编写一个button,Command绑定一个命令 <Grid><ButtonWidth"100"Height"40" Command"{Binding ShowCommand}"></Button> </Grid>2、编写一个model.cs namespace WPF_Le…...
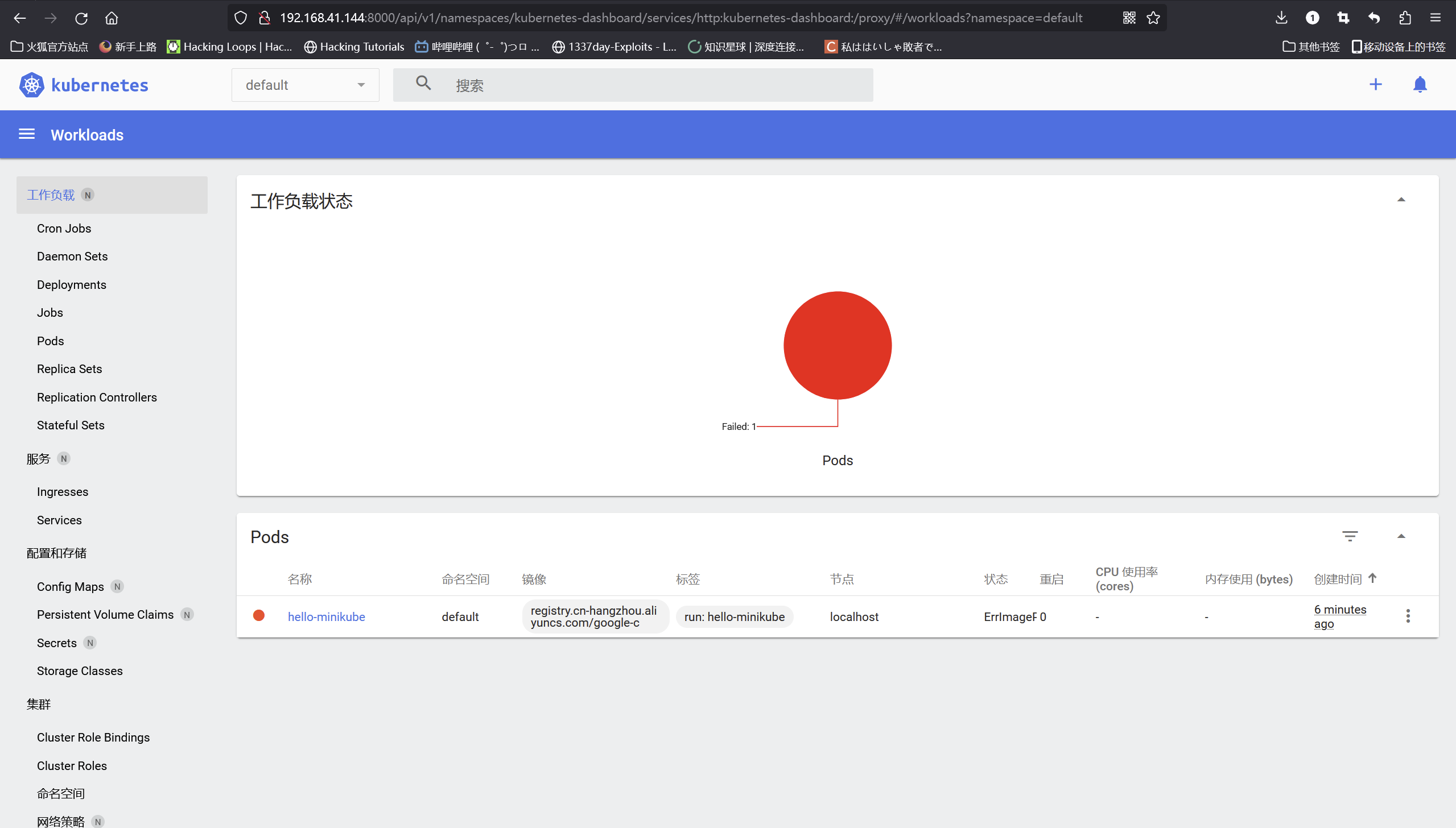
云安全攻防(十三)之 使用minikube安装搭建 K8s 集群
使用minikube安装搭建 K8s 集群 Kubernetes 是一个可移植的、可扩展的开源平台,用于管理容器化的工作负载和服务,可促进声明式配置和自动化,一般来说K8s安装有三种方式,分别是Minikube装搭建 K8s 集群,特点是只有一个节点的集群&…...

Python数据分析 | 各种图表对比总结
本期将带领大家一起对在数据可视化的过程中常用的一些图表进行下总结: 条形图 【适用场景】 适用场合是二维数据集(每个数据点包括两个值x和y),但只有一个维度需要比较,用于显示一段时间内的数据变化或显示各项之间的…...

linux系统(centos、ubuntu、银河麒麟服务、uos、deepin)判断程序是否已安装,通用判断方法:适用所有应用和命令的判断
前言 项目中需要判断linux服务器中是否已经安装了某个服务 方法有很多种,但是很多都不通用, 脚本代码就不容易做成统一的 解决方案 用下面的脚本代码去进行判断 用jdk测试 脚本意思如下: 输入java -version命令,将返回的字…...
Python3多线程/多进程解决方案(持续更新ing...)
诸神缄默不语-个人CSDN博文目录 文章目录 1. 多线程2. 多进程示例1:multiprocessing.Pool直接实现对一个列表中的每个元素的函数操作示例2:使用苏神写的工具函数实现对一个迭代器中每个元素的函数操作 1. 多线程 2. 多进程 示例1:multiproc…...

在`CentOS`中安装`Docker Engine`
本文总结如何在CentOS中安装Docker Engine 〇、Docker Engine 介绍 Docker Engine是一种开源容器化技术,用于构建和容器化应用程序。Docker引擎作为一个客户端-服务器应用程序: 具有长时间运行守护进程的服务器。指定接口的api,程序可以使用这些接口与…...
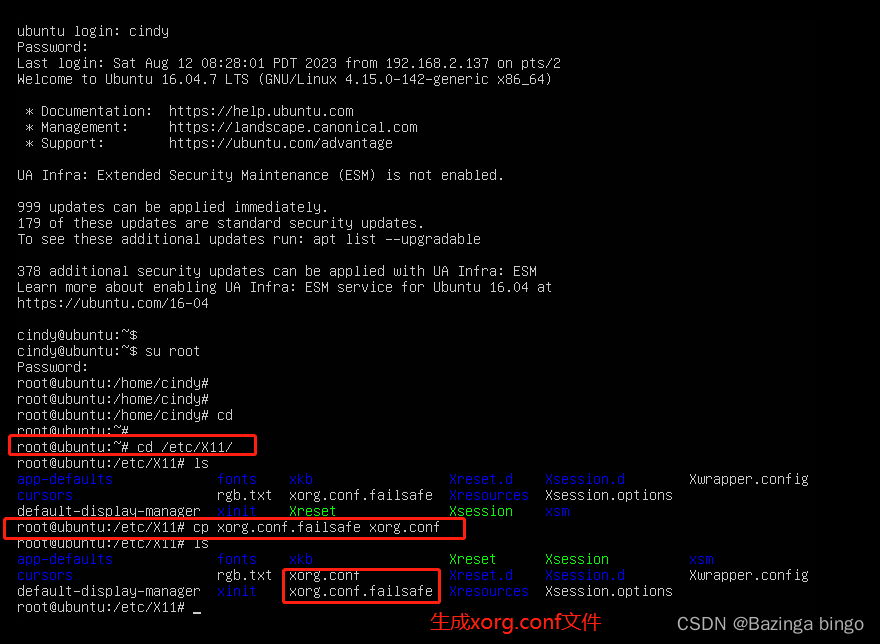
[ VMware 虚拟机 ] 启动不了图形界面,报 “The system is running in low-graphics mode” 错误
文章目录 问题现象异常原因解决方案 问题现象 在启动虚拟机的时候,不能正常的进入图形界面,报 “The system is running in low-graphics mode” 错误。 异常原因 启动界面的xorg.conf文件失败并删除。 解决方案 1、点击异常界面上的 “ok”后&…...
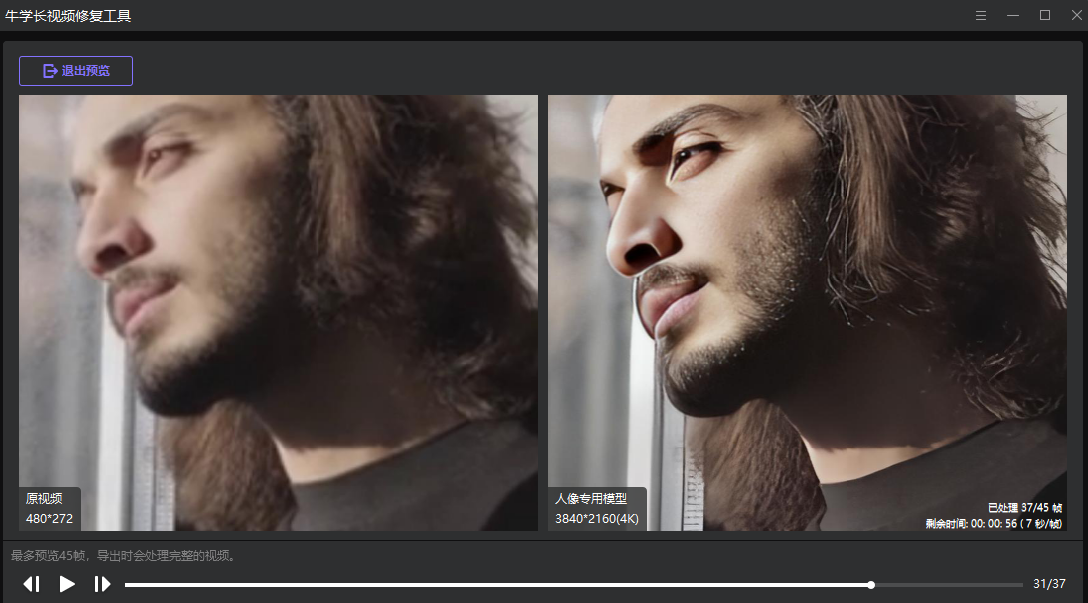
如何提高视频清晰度?视频调整清晰度操作方法
现在很多小伙伴通过制作短视频发布到一些短视频平台上记录生活,分享趣事。但制作的视频有些比较模糊,做视频的小伙伴应该都知道,视频画质模糊不清,会严重影响观众的观看体验。 通过研究,总结了以下几点严重影响的点 …...

IO进程线程,文件与目录,实现linux任意目录下ls -la
注意文件的名字、路径是如何输入的。 函数opendir打开目录,struct dirent,struct stat这些结构体的含义。 readdir()函数是一个用于读取目录内容的系统调用或库函数,在类Unix操作系统中(如Linux)广泛使用。它用于遍历…...
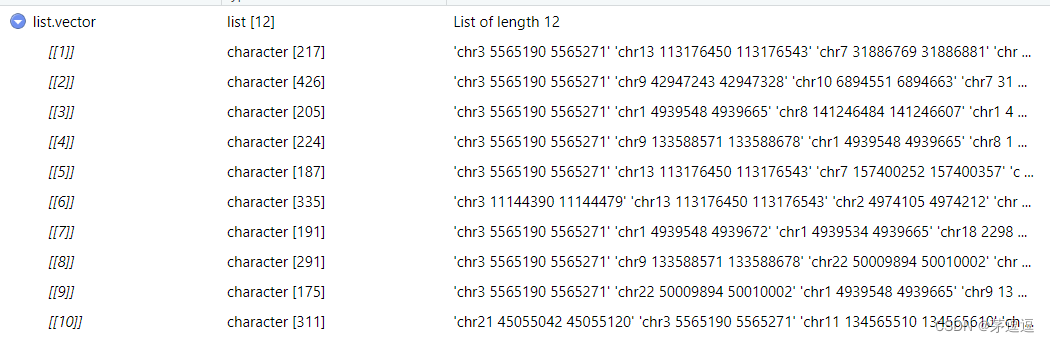
R语言如果列表中有列表,且每个子列表有一个向量:如何转变为仅仅一个列表里面含有向量
引言 有些时候,比如批量读取表格中的某一列的时候,最终你会得到列表里面装列表,且每个列表里面只有一个向量的情况。我们的目标是不要中间这一层列表,而是直接变成列表-向量这种简单的结构,如何完成呢。我觉得有很多方…...
nrm管理源仓库及发布私人npm包
使用nrm管理源及切换源仓库 1.安装nrm源管理器 npm install nrm -g2.查看目前现有的源仓库 通过 nrm ls 查看现有的源 nrm ls 输出:这是目前现有的源 3.切换不同的源 可以通过 nrm use xxx(源仓库名)来切换不同的源地址 nrm use taobao…...

云计算——虚拟化中的网络架构与虚拟网络(文末送书)
作者简介:一名云计算网络运维人员、每天分享网络与运维的技术与干货。 公众号:网络豆 座右铭:低头赶路,敬事如仪 个人主页: 网络豆的主页 目录 前期回顾 前言 一.网卡虚拟化 1.网卡虚拟化方法&…...

B - 负环
题目描述 给定一个 n 个点的有向图,请求出图中是否存在从顶点 11 出发能到达的负环。 负环的定义是:一条边权之和为负数的回路。 输入格式 本题单测试点有多组测试数据。 输入的第一行是一个整数 T,表示测试数据的组数。对于每组数据的格…...
)
居中一个元素(水平+垂直居中)
我们的示例代码全在此基础上修改: ...... <style>* {margin: 0;padding: 0;}.par {width: 600px;height: 400px;background-color: antiquewhite;display: flex;justify-content: center;align-items: center;}.chi1 {width: 60px;height: 40px;backgrou…...

React笔记(二)JSX
一、JSX JSX是javascript XML的简写,实际上是javascript的扩展,既有javascript的语法结构,又有XML的结构 1、JSX的规则要求 jsx必须要有一个根节点 如果不想产生无用的根标签,但是还要遵守JSX的语法的要求,可以使用…...

[多标签分类]MultiLabelBinarizer: 从one-hot 到multi-hot
]MultiLabelBinarizer: 从one-hot 到multi-hot 背景知识One hot encoderLabelEncoderMultiLabelBinarizer总结 背景知识 多类别分类: label space至少有3个label, 且默认每个sample有一个label, 与之相对应的是二元分类Binary classification, 多标签分类: 每个sample有1至多…...

【校招VIP】前端算法考察之排序
考点介绍: 不同的场景中,不同的排序算法执行效率不同。 稳定:冒泡、插入、归并 不稳定:选择、快速、堆排序、希尔排序 『前端算法考察之排序』相关题目及解析内容可点击文章末尾链接查看! 一、考点题目 1、使用js实…...
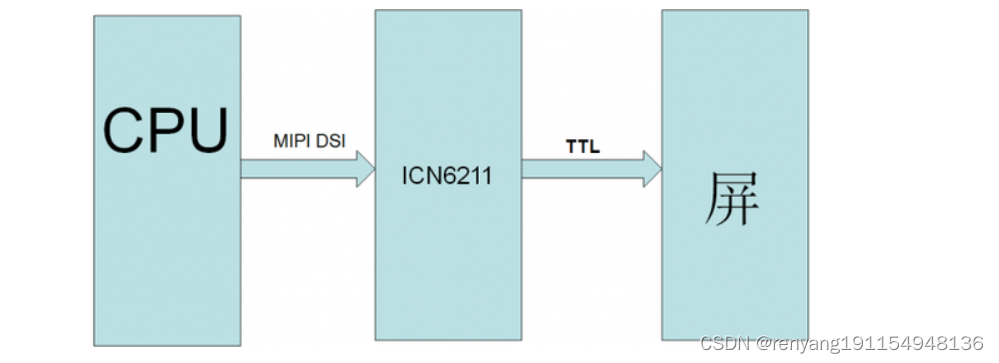
集创北方ICN6211 是一款MIPIDSI转RGB视频桥接IC
ICN6211 1.描述: ICN6211是一个桥接芯片,它接收MIPIDSI输入并发送RGB输出。MIPIDSI最多支持4个车道, 每个车道的最大运行频率为1Gbps;总最大输入带宽为4Gbps;并且还支持MIPI定义的ULPS(超 低功耗状态&a…...

SMT制造中的产品质量检验和管理
SMT制造中的质量检验和产品物料管理都是实现高质量、低成本、高效益的重要方法。在SMT加工的过程中,产品质量的检验和质量把控都是重中之重,可以有效的降低产品不良率及返修等造成制造成本升高的风险问题,今天就来跟大家讨论一下SMT制造中我们…...
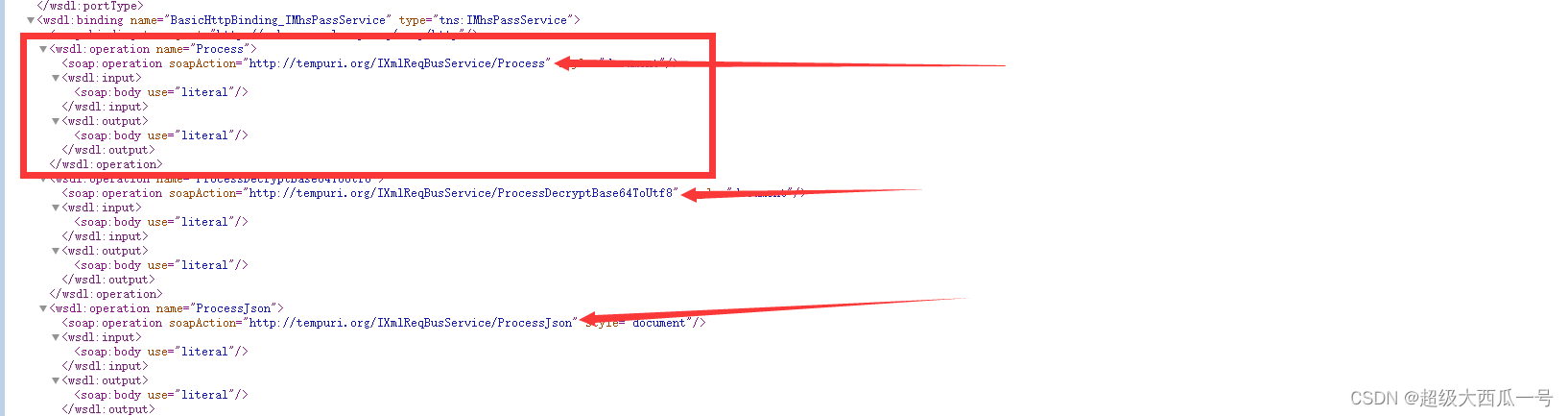
对接webservice接口时报错:发送方和接收方 Action 不匹配
趁着早上有时间,赶紧记录一下,哈哈。 错误提示如下: 1、英文版: <s:Envelope xmlns:s“http://schemas.xmlsoap.org/soap/envelope/”><s:Body><s:Fault>a:ActionNotSupportedThe message with Action ‘’ ca…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...
