【leetcode刷题之路】剑指Offer(4)——分治+排序算法+动态规划
文章目录
- 8 分治算法
- 8.1 【递归】剑指 Offer 07 - 重建二叉树
- 8.2 【递归】【快速幂】剑指 Offer 16 - 数值的整数次方
- 8.3 【递归】剑指 Offer 33 - 二叉搜索树的后序遍历序列
- 8.4 【递归】【分治】剑指 Offer 17 - 打印从1到最大的n位数
- 8.5 【归并排序】【分治】剑指 Offer 51 - 数组中的逆序对
- 9 排序
- 9.1 【冒泡排序】剑指 Offer 45 - 把数组排成最小的数
- 9.2 【排序】剑指 Offer 61 - 扑克牌中的顺子
- 9.3 【堆排序】剑指 Offer 40 - 最小的k个数
- 9.4 【堆排序】【优先队列】剑指 Offer 41 - 数据流中的中位数
- 10 动态规划
- 10.1 【动态规划】【哈希表】【DFS】剑指 Offer 10- I - 斐波那契数列
- 10.2 【动态规划】【哈希表】【DFS】剑指 Offer 10- II - 青蛙跳台阶问题
- 10.3 【动态规划】剑指 Offer 63 - 股票的最大利润
- 10.4 【动态规划】【分治】剑指 Offer 42 - 连续子数组的最大和
- 10.5 【动态规划】剑指 Offer 47 - 礼物的最大价值
8 分治算法
8.1 【递归】剑指 Offer 07 - 重建二叉树
https://leetcode.cn/problems/zhong-jian-er-cha-shu-lcof/
前序遍历是根左右,中序遍历是左根右,这也就意味着前序遍历的第一个节点是整棵树的根节点,顺着这个节点找到它在中序遍历中的位置,即为in_root,那么in_root左边的都在左子树,右边的都在右子树,这样就可以知道左子树一共有多少个节点,然后去前序遍历中找到左右子树的分界点,分成左右两部分,分别重复上述过程,找到各自部分的第一个根节点,然后再依次往下进行,直到最后左右子树的边界发生重合,此时二叉树重建完毕。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
private:unordered_map<int,int> hash_table;
public:TreeNode* subTree(vector<int>& preorder, vector<int>& inorder, int pre_l, int pre_r, int in_l, int in_r){if(pre_l > pre_r) return nullptr;//找到根节点,计算左子树的节点数int pre_root = pre_l;int in_root = hash_table[preorder[pre_l]];int sub_l = in_root - in_l;//开始生成rootTreeNode* root = new TreeNode(preorder[pre_l]);//对于左子树而言,前序遍历的[左边界+1,左边界+左子树节点数]即为中序遍历的[左边界,根节点-1]root->left = subTree(preorder, inorder, pre_l+1, pre_l+sub_l, in_l, in_root-1);//对于右子树而言,前序遍历的[左边界+左子树节点数+1,右边界]即为中序遍历的[根节点+1,右边界]root->right = subTree(preorder, inorder, pre_l+sub_l+1, pre_r, in_root+1, in_r);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int n = inorder.size();for(int i=0;i<n;i++){hash_table[inorder[i]] = i;}return subTree(preorder, inorder, 0, n-1, 0, n-1);}
};
8.2 【递归】【快速幂】剑指 Offer 16 - 数值的整数次方
https://leetcode.cn/problems/shu-zhi-de-zheng-shu-ci-fang-lcof/description/
这道题可以用快速幂来解决,具体思路就是把幂次按照二进制拆开,分别计算,下面举个例子: 假设我要计算 x 10 x^{10} x10,因为10的二进制表示为1010,那么 x 10 = x 2 0 ∗ 0 ∗ x 2 1 ∗ 1 ∗ x 2 2 ∗ 0 ∗ x 2 3 ∗ 1 x^{10}=x^{2^0*0}*x^{2^1*1}*x^{2^2*0}*x^{2^3*1} x10=x20∗0∗x21∗1∗x22∗0∗x23∗1,可以看作按照x的2次方依次递增,只需要看这一个次方对应的二进制是否为1。
class Solution {
public:double myPow(double x, int n) {if(x==1 || n==0) return 1;if(x==0) return 0;double ans = 1;long num = n;if(n<0){num = -num;x = 1/x;}while(num){if(num & 1) ans *= x;x *= x;num >>= 1;}return ans;}
};
8.3 【递归】剑指 Offer 33 - 二叉搜索树的后序遍历序列
https://leetcode.cn/problems/er-cha-sou-suo-shu-de-hou-xu-bian-li-xu-lie-lcof
后序遍历的特点就是先访问左子树再访问右子树最后访问根节点,所以最后一个元素一定根节点,而二叉搜索树的特点就是左子树<根节点<右子树,所以我们可以根据根节点的值把数组分为两部分,然后分别判断是否符合二叉搜索树的特点,重复上述过程直到所有情况都判断完为止。
class Solution {
public:bool dfs(vector<int>& postorder, int left, int right){if(left >= right) return true;int i = left;while(postorder[i]<postorder[right]){i++;}int mid = i;while(postorder[i]>postorder[right]){i++;}return i==right & dfs(postorder,left,mid-1) & dfs(postorder,mid,right-1);}bool verifyPostorder(vector<int>& postorder){return dfs(postorder,0,postorder.size()-1);}
};
8.4 【递归】【分治】剑指 Offer 17 - 打印从1到最大的n位数
https://leetcode.cn/problems/da-yin-cong-1dao-zui-da-de-nwei-shu-lcof
这道题目由于指定了数组是int型,所以不用考虑大整数问题,直接暴力就可以解决,但如果是大整数的话,需要采用分治递归的思想,主要如下:
(1)第一层遍历,为n,分别考虑到生成的数字是1位数、2位数、3位数…n位数;
(2)第二层遍历,分别遍历每一位数是几,除了第一位是1-9之外,其余都是0-9。
class Solution {
public:vector<int> printNumbers(int n) {int cnt = pow(10,n);vector<int> ans;for(int i=1;i<cnt;i++){ans.push_back(i);}return ans;}
};
8.5 【归并排序】【分治】剑指 Offer 51 - 数组中的逆序对
https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof
这位大佬写的很好!(https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/solutions/622496/jian-zhi-offer-51-shu-zu-zhong-de-ni-xu-pvn2h)
class Solution {
public:int merge_sort(int left, int right, vector<int>& nums, vector<int>& tmp){if(left >= right) return 0;int mid = (left + right) / 2;int res = merge_sort(left, mid, nums, tmp) + merge_sort(mid+1, right, nums, tmp);int i = left, j = mid + 1;for(int k=left;k<=right;k++){tmp[k] = nums[k];}for(int k=left;k<=right;k++){ if(i == mid+1) nums[k] = tmp[j++];else if(j == right+1 || tmp[i] <= tmp[j]) nums[k] = tmp[i++];else{nums[k] = tmp[j++];res += mid - i + 1;}}return res;}int reversePairs(vector<int>& nums){vector<int> tmp(nums.size());return merge_sort(0, nums.size()-1, nums, tmp);}
};
9 排序
9.1 【冒泡排序】剑指 Offer 45 - 把数组排成最小的数
https://leetcode.cn/problems/ba-shu-zu-pai-cheng-zui-xiao-de-shu-lcof
这题可以看作是冒泡排序,只不过针对的对象是字符串,我们需要找到里面表示最大的字符串,然后把它放到字符串的最后即可,例如“32”和“3”,因为“323”<“332”,所以“32”<“3”,所以应该把“3”放在“32”后面,借助这种排序思路来解题。
class Solution {
public:string minNumber(vector<int>& nums) {for(int i=nums.size()-1;i>0;i--){for(int j=0;j<i;j++){if(string_sort(nums[j],nums[j+1])){swap(nums[j],nums[j+1]);}}}string ans = "";for(int i=0;i<nums.size();i++){ans += to_string(nums[i]);}return ans;}bool string_sort(int num1, int num2){string s1 = to_string(num1) + to_string(num2);string s2 = to_string(num2) + to_string(num1);if(s1>s2) return true;else return false;}
};
9.2 【排序】剑指 Offer 61 - 扑克牌中的顺子
https://leetcode.cn/problems/bu-ke-pai-zhong-de-shun-zi-lcof
这道题不难,想清楚顺子的判断条件即可,主要为以下几个方面:
(1)五个数中除了0以外不能有其他的重复数字,否则肯定不是顺子;
(2)找出五个数中的最大值和最小值,看看这两个数之间缺的数的个数是多少,记为gap,然后计算五个数中0的个数,记为zero_num,如果gap<=zero_num,说明0的个数可以补全缺的数,否则就肯定不是顺子。
class Solution {
public:bool isStraight(vector<int>& nums) {int arr[14] = {0};int max_num = 0, min_num = 14, zero_num = 0;for(int i=0;i<5;i++){if(nums[i]==0) zero_num++;else{if(arr[nums[i]]) return false;else{arr[nums[i]] = 1;min_num = min(min_num, nums[i]);max_num = max(max_num, nums[i]);}}}int gap = 0;for(int i=min_num;i<max_num;i++){if(arr[i]!=1) gap++;}if(gap <= zero_num) return true;else return false;}
};
9.3 【堆排序】剑指 Offer 40 - 最小的k个数
https://leetcode.cn/problems/zui-xiao-de-kge-shu-lcof
方法一:直接用sort排序,然后选前k个数就好了。
方法二:用堆排序,堆排序,采用大根堆,首先把前k个数字存入大根堆中,之后的数字依次和大根堆的top比较,如果比top小就更新大根堆,最后把大根堆中的数字存入vector中作为答案返回。
//方法一:直接排序
class Solution {
public:vector<int> getLeastNumbers(vector<int>& arr, int k) {sort(arr.begin(),arr.end());vector<int> ans;for(int i=0;i<k;i++){ans.push_back(arr[i]);}return ans;}
};
//方法二:堆排序
class Solution {
public:vector<int> getLeastNumbers(vector<int>& arr, int k) {vector<int> ans;if(k == 0) return ans;priority_queue<int, vector<int>, less<int>> max_stack;//把前k个数字存入大根堆for(int i=0;i<k;i++){max_stack.push(arr[i]);}//依次和大根堆的top比较,如果比top小就更新大根堆for(int j=k;j<arr.size();j++){if(arr[j] < max_stack.top()){max_stack.pop();max_stack.push(arr[j]);}}//把大根堆中的数字存入vector中作为答案返回while(k--){ans.push_back(max_stack.top());max_stack.pop();}return ans;}
};
9.4 【堆排序】【优先队列】剑指 Offer 41 - 数据流中的中位数
https://leetcode.cn/problems/shu-ju-liu-zhong-de-zhong-wei-shu-lcof
这道题如果直接对所有数进行排序的话,最后会runtime,其实只要能找出每一次执行findMedian函数时整个数据流中间的两个数或者一个数就行了,这是我们可以考虑用堆排序,同时维持一个大根堆和一个小根堆,把数据流中的数分为两部分,同时也要保证大根堆中的top要比小根堆中的top小,这样最后的中位数要么是小根堆top,要么就是大根堆和小根堆的top取平均,构造方法如下:
- 如果大根堆和小根堆的size一样,那么此时add的num就加入大根堆,然后把大根堆的top插入到小根堆中,保证大根堆的size<=小根堆的size;
- 如果大根堆和小根堆的size不一样,那么此时add的num就加入小根堆,然后把小根堆的top插入到大根堆中,保证小根堆的size<=大根堆的size;
- 执行findMedian函数时,看看此时大根堆和小根堆的size是否相等,如果相等的话,中位数就是各自取top元素相加取平均,如果不相等,那么中位数就是小根堆的top。
class MedianFinder {
public:/** initialize your data structure here. */priority_queue<int, vector<int>, greater<int>> min_stack;priority_queue<int, vector<int>, less<int>> max_stack;MedianFinder() {}void addNum(int num) {//如果大根堆和小根堆的size一样,那么此时add的num就加入大根堆,然后把大根堆的top插入到小根堆中,保证大根堆的size<=小根堆的sizeif(min_stack.size() == max_stack.size()){max_stack.push(num);min_stack.push(max_stack.top());max_stack.pop();}//如果大根堆和小根堆的size不一样,那么此时add的num就加入小根堆,然后把小根堆的top插入到大根堆中,保证小根堆的size<=大根堆的sizeelse{min_stack.push(num);max_stack.push(min_stack.top());min_stack.pop();}}//执行findMedian函数时,看看此时大根堆和小根堆的size是否相等,如果相等的话,中位数就是各自取top元素相加取平均,如果不相等,那么中位数就是小根堆的topdouble findMedian() {if(min_stack.size() == max_stack.size()){return (max_stack.top() + min_stack.top()) / 2.0;}else return min_stack.top();}
};/*** Your MedianFinder object will be instantiated and called as such:* MedianFinder* obj = new MedianFinder();* obj->addNum(num);* double param_2 = obj->findMedian();*/
10 动态规划
10.1 【动态规划】【哈希表】【DFS】剑指 Offer 10- I - 斐波那契数列
https://leetcode.cn/problems/fei-bo-na-qi-shu-lie-lcof
这道题如果直接用动态规划会runtime,主要是因为在计算过程中会有一些数被反复计算,所以我们在这里采用哈希表来存放已经被计算过的数,这样在之后再次被计算时直接用就好了。
class Solution {
public:unordered_map<int,int> hash_table;int dfs(int n){if(n == 0) return 0;else if(n == 1) return 1;else{if(hash_table.count(n)) return hash_table[n];else{int num1 = dfs(n-1) % 1000000007;int num2 = dfs(n-2) % 1000000007;hash_table[n] = (num1 + num2) % 1000000007;return hash_table[n];}}}int fib(int n) {return dfs(n);}
};
10.2 【动态规划】【哈希表】【DFS】剑指 Offer 10- II - 青蛙跳台阶问题
https://leetcode.cn/problems/qing-wa-tiao-tai-jie-wen-ti-lcof
这道题目就是变形的斐波那契数列,在这里采用哈希表来存放已经被计算过的数,这样在之后再次被计算时直接用就好了。
class Solution {
public:unordered_map<int,int> hash_table;int dfs(int n){if(n == 0) return 1;else if(n == 1) return 1;else{if(hash_table.count(n)) return hash_table[n];else{int num1 = dfs(n-1) % 1000000007;int num2 = dfs(n-2) % 1000000007;hash_table[n] = (num1 + num2) % 1000000007;return hash_table[n];}}}int numWays(int n) {return dfs(n);}
};
10.3 【动态规划】剑指 Offer 63 - 股票的最大利润
https://leetcode.cn/problems/gu-piao-de-zui-da-li-run-lcof
动态规划类题目的解题主要是找到状态转移方程就好了,对于这道题目的状态转移就在于某一天有无股票,我们以此为分界来定义状态转移方程dp[i][2]:
(1)前i天未持有股票
d p [ i ] [ 0 ] = m a x ( d p [ i − 1 ] [ 0 ] , d p [ i − 1 ] [ 1 ] + p r i c e s [ i ] ) dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]) dp[i][0]=max(dp[i−1][0],dp[i−1][1]+prices[i])
(2)前i天持有股票
d p [ i ] [ 1 ] = m a x ( d p [ i − 1 ] [ 1 ] , 0 − p r i c e s [ i ] ) dp[i][1] = max(dp[i-1][1], 0 - prices[i]) dp[i][1]=max(dp[i−1][1],0−prices[i])
同时还要预判一下prices为空的情况,此时返回0,因为dp的两个元素在反复调用,所以在代码中也是直接用两个变量来进行代替了。
class Solution {
public:int maxProfit(vector<int>& prices) {if(!prices.size()) return 0;int dp_0 = 0, dp_1 = -prices[0];for(int i=1;i<prices.size();i++){dp_0 = max(dp_0, dp_1 + prices[i]);dp_1 = max(dp_1, 0 - prices[i]);}return dp_0;}
};
10.4 【动态规划】【分治】剑指 Offer 42 - 连续子数组的最大和
https://leetcode.cn/problems/lian-xu-zi-shu-zu-de-zui-da-he-lcof
这道题用到一点点分治的思想,假设现在数组长度为 n n n,连续子数组的最大和为 f ( n ) f(n) f(n),那么 f ( n ) = m a x ( f ( n − 1 ) + n u m s [ i ] , n u m [ i ] ) f(n)=max(f(n-1)+nums[i],num[i]) f(n)=max(f(n−1)+nums[i],num[i]),也就意味着最大和要么是前 n − 1 n-1 n−1个数的最大和加上第 i i i个数,要么就是第 i i i个数本身,如果是第 i i i个数本身的话,就要从这里开始重新找到连续子数组了,在这个过程中记录下最大值即可。
class Solution {
public:int maxSubArray(vector<int>& nums) {int pre = 0, max_seqsum = nums[0];for(int i=0;i<nums.size();i++){pre = max(pre + nums[i], nums[i]);max_seqsum = max(max_seqsum, pre);}return max_seqsum;}
};
10.5 【动态规划】剑指 Offer 47 - 礼物的最大价值
https://leetcode.cn/problems/li-wu-de-zui-da-jie-zhi-lcof
其实每个地方的最大值只与两个状态有关,假设目前要求的是 v a l u e [ i ] [ j ] value[i][j] value[i][j]的最大值,那么 v a l u e [ i ] [ j ] = m a x ( v a l u e [ i ] [ j − 1 ] , v a l u e [ i − 1 ] [ j ] ) + g r i d [ i ] [ j ] value[i][j] = max(value[i][j-1],value[i-1][j]) + grid[i][j] value[i][j]=max(value[i][j−1],value[i−1][j])+grid[i][j],这里为了方便初始化,把初始数组的大小设置为 ( m + 1 ) ∗ ( n + 1 ) (m+1)*(n+1) (m+1)∗(n+1)。
class Solution {
public:int maxValue(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();int value[m+1][n+1];memset(value,0,sizeof(value));for(int i=0;i<m;i++){for(int j=0;j<n;j++){value[i+1][j+1] = max(value[i+1][j],value[i][j+1]) + grid[i][j];}}return value[m][n];}
};
相关文章:
——分治+排序算法+动态规划)
【leetcode刷题之路】剑指Offer(4)——分治+排序算法+动态规划
文章目录 8 分治算法8.1 【递归】剑指 Offer 07 - 重建二叉树8.2 【递归】【快速幂】剑指 Offer 16 - 数值的整数次方8.3 【递归】剑指 Offer 33 - 二叉搜索树的后序遍历序列8.4 【递归】【分治】剑指 Offer 17 - 打印从1到最大的n位数8.5 【归并排序】【分治】剑指 Offer 51 -…...

美创科技“签”手柠檬文才学堂,共推高校数据安全建设
近日,由柠檬文才学堂联合中国教育在线、东北财经大学网络教育学院共同主办的“三教统筹下高校继续教育数字化转型研讨”顺利召开。 国内高等院校(高职院校)继续教育分管领导,继续教育学院领导及继续教育信息化、教学教务管理、课程…...
【JAVA基础】数据类型,逻辑控制
❤️ Author: 老九 ☕️ 个人博客:老九的CSDN博客 🙏 个人名言:不可控之事 乐观面对 😍 系列专栏: 文章目录 数据类型整型变量 int长整型变量 long单精度浮点数 float双精度浮点数 double字符类型 char字节…...
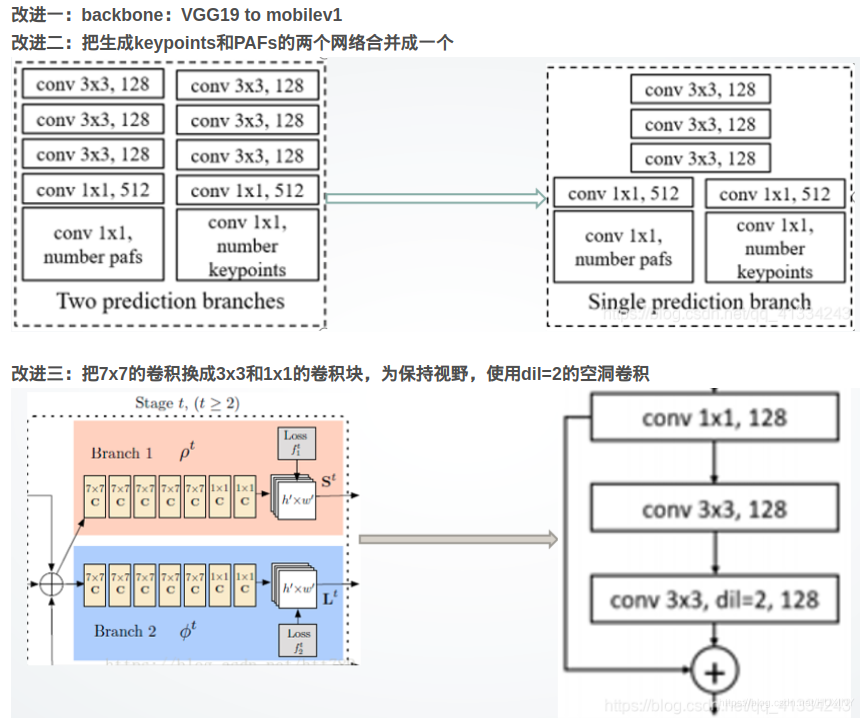
计算机竞赛 基于图像识别的跌倒检测算法
前言 🔥 优质竞赛项目系列,今天要分享的是 基于图像识别的跌倒检测算法 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🧿 更多资料, 项目分享: https://gitee.com/dancheng-senior/…...
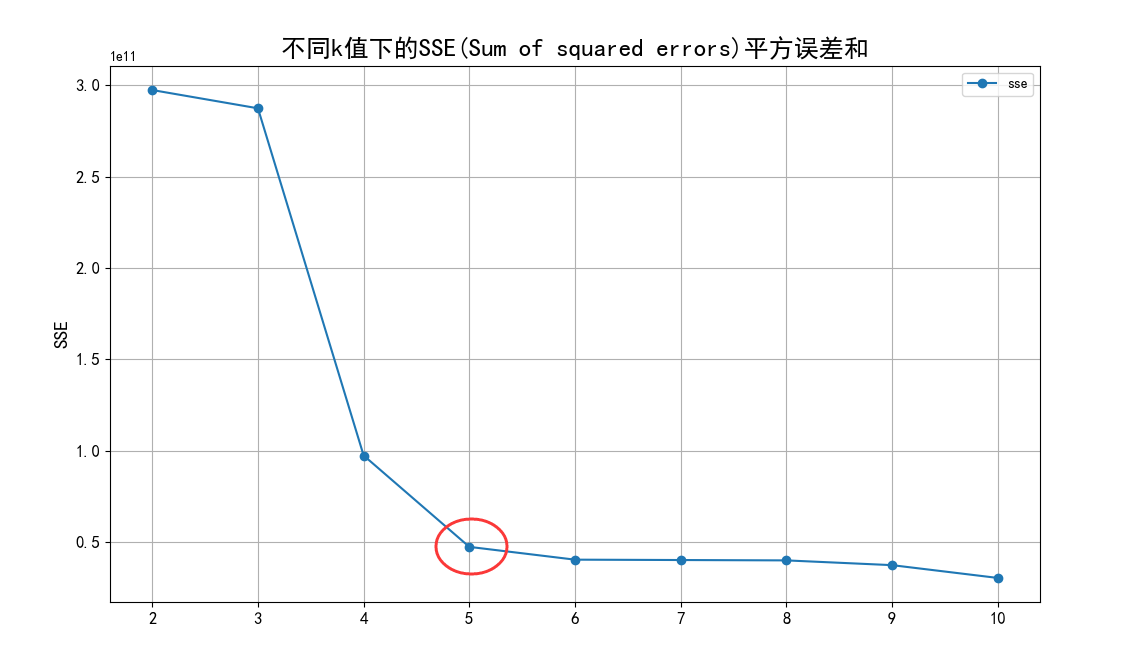
计算机竞赛 基于大数据的股票量化分析与股价预测系统
文章目录 0 前言1 课题背景2 实现效果3 设计原理QTChartsarma模型预测K-means聚类算法算法实现关键问题说明 4 部分核心代码5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 基于大数据的股票量化分析与股价预测系统 该项目较为新颖…...

input子系统
内核分三层 1、事件处理层 2、核心层 3、设备驱动层 当硬件按下,在设备驱动中触发中断,中断程序会将事件上报给核心层 核心层将事件给事件处理层,最后事件处理层控制app应用层的怎么操作将数据发送到用户空间...

mac 10.13.6安装后开发准备工作
git下载安装 xcode旧版安装搜索 brew国内源安装 brew国内源安装地址2 brew更换源 SwitchHosts github hosts nfts磁盘读写工具 更新ssl证书 证书下载 然后备份一下系统原来的pem文件 cp /etc/ssl/cert.pem /etc/ssl/cert.bak.pem 之后将新下载的pem文件,拷贝到/etc…...

C++ using关键字
C using关键字 using关键字用来简化代码和提高可读性。 using关键字提供了一种灵活的方式,可以在C中导入命名空间和定义别名。 1. 导入命名空间 using namespace 可以将一个命名空间中的所有名称导入到当前作用域中,从而可以直接使用该命名空间中的所…...

让你对es有一个初步的了解
首先es在海量数据的搜索能力非常好,es你可以把他看成一个搜索引擎数据库,他是个非关系型数据库。他的语法有很大的不同,好像都是json风格的。还有一点需要说的就是es 的数据是存在硬盘上的, 我们先来看一下mysql和es的区别吧。一…...
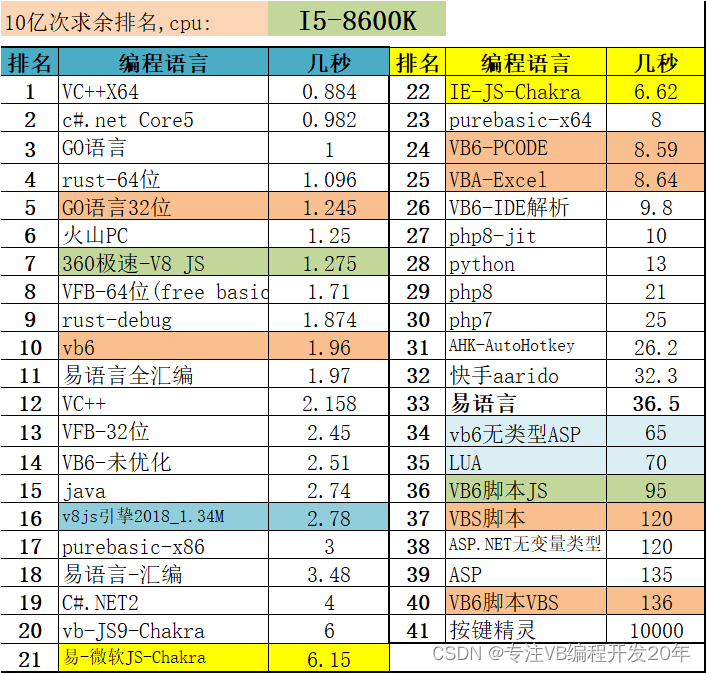
编绎和优化,脚本代码小米加步枪赶超英法美
编程达人:冰冻牡蛎 测试,总结》》 今有空,继续看了一下竹笋大师几天前提出的“使用for循环查找10亿内可被7整除的数的个数”的题目(相关文件:群文件 10亿以内多少个数字可以整除7.7z ) 1. 论输出的exe大小…...
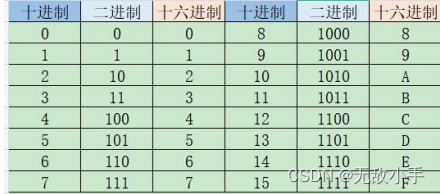
数字电路-二进制学习
什么是二进制? 数字电路 中 只有 高电平 和低电平 就是 1 和0 进位规则是“逢二进一”,借位规则是“借一当二”。 二进制、八进制 、十进制、十六进制 二进制 有两个数来表示 : 0、1 八进制 有8个数来表示 : 0、1、2、3、4、…...

运维Shell脚本小试牛刀(一)
运维Shell脚本小试牛刀(一) 运维Shell脚本小试牛刀(二) 一: Shell中循环剖析 for 循环....... #!/bin/bash - # # # # FILE: countloop.sh # USAGE: ./countloop.sh # DESCRIPTION: # OPTIONS: ------- # …...

screen命令,可以断开服务器连接,依旧能运行你的程序了
可以参考博客1:https://blog.csdn.net/nima_zhang_b/article/details/82797928 可以参考博客2:https://blog.csdn.net/herocheney/article/details/130984403 Linux中的screen是一个命令行工具,可以让用户在同一个终端会话中创建多个虚拟终端。它非常有…...
【ArcGIS Pro二次开发】(63):批量更改字段别名
在我工作中遇到的大多数图斑,字段名称一般是英文,字段别名是中文,使用起来是比较方便的。 但有时候也会遇到一些不一样的情况,不知是经过了怎样的处理,图斑的字段别名被修改成了和字段名称一样的英文,这样…...

redis全套参数配置及降级解决方案
文章目录 redis高可用核心参数配置1.Lettuce2.Jedis3.Redisson4.其他客户端 redis降级场景简介一、业务背景二、设计方案三、实现方案四、总结 redis高可用核心参数配置 1.Lettuce 提示:该客户端无主动探活机制,只能依赖于 OS KeepaAlive 机制…...

AMD即将上市大量中端显卡,为新显卡支付过高价格的日子可能结束
AMD在本周末(8月25日)的德国Gamescom活动中展示了两款新显卡和一些新的升级技术,这些新GPU的定价将与英伟达的GeForce RTX 4000卡竞争。 这是一件大事,因为新的Radeon RX 7700 XT和7800 XT卡占据了AMD Radeon RX 7000系列产品线…...

go学习一之go的初体验
go语言学习笔记 一、golang初体验: 1.简单体验案例: package main{ //把这个test.go归属到main import "fmt" //引入一个包 func main(){//输出hellofmt.Println("hello world")} }2.从案例学到的知识点: (1) go文件的后缀是.…...

智能制造产业链数字化转型、数字化互联工厂建设方案PPT
本资料来源公开网络,仅供个人学习,请勿商用,如有侵权请联系删除,更多浏览公众号:智慧方案文库 篇幅有限,无法完全展示,喜欢资料可转发评论,私信了解更多信息。...

【安卓】拿注册码的两种方式
【安卓】拿注册码的两种方式 文章仅用于学习交流,请勿利用文章中的技术对任何计算机系统进行入侵操作。利用此文所提供的信息而造成的直接或间接后果和损失,均由使用者本人负责。首发吾爱:https://www.52pojie.cn/thread-1826802-1-1.html言归…...
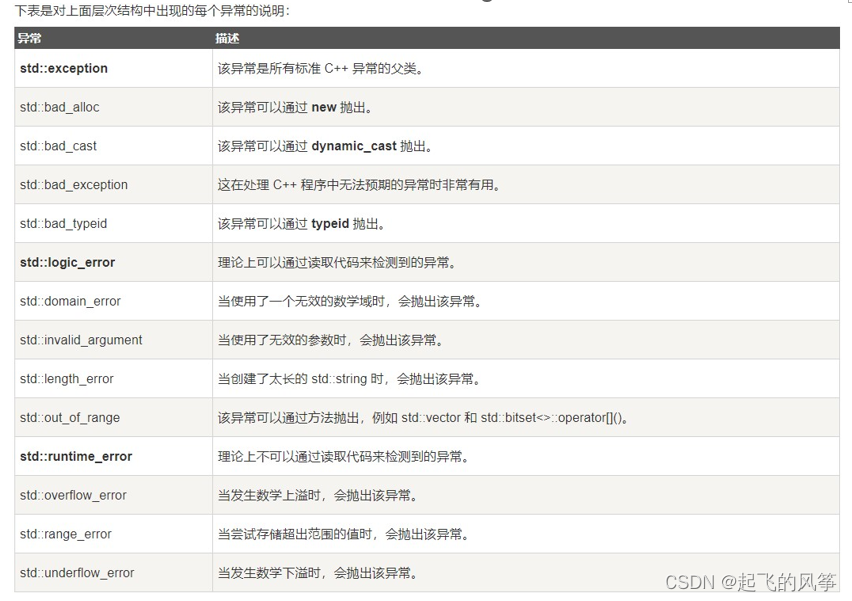
【C++】—— 异常处理
前言: 本期,我将给大家讲解的是有关 异常处理 的相关知识! 目录 (一)C语言传统的处理错误的方式 (二)C异常概念 (三)异常的使用 1、异常的抛出和捕获 1️⃣ 异常的…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...
