Python之动态规划
序言
最近在学习python语言,语言有通用性,此文记录复习动态规划并练习python语言。
动态规划(Dynamic Programming)
动态规划是运筹学的一个分支,是求解决策过程最优化的过程。20世纪50年代初,美国数学家贝尔曼(R.Bellman)等人在研究多阶段决策过程的优化问题时,提出了著名的最优化原理,从而创立了动态规划。动态规划的应用极其广泛,包括工程技术、经济、工业生产、军事以及自动化控制等领域,并在背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等中取得了显著的效果。
基本思想:将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。
斐波那契数列(Fibonacci sequence)
斐波那契数列,又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称“兔子数列”,其数值为:1、1、2、3、5、8、13、21、34……在数学上,这一数列以如下递推的方法定义:F(0)=1,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)。
先以斐波那契数列为例,了解动态规划。
def fibonacci(num):if num == 0:return 1if num == 1:return 1return fibonacci(num - 1) + fibonacci(num - 2)if __name__ == "__main__":print(fibonacci(10))
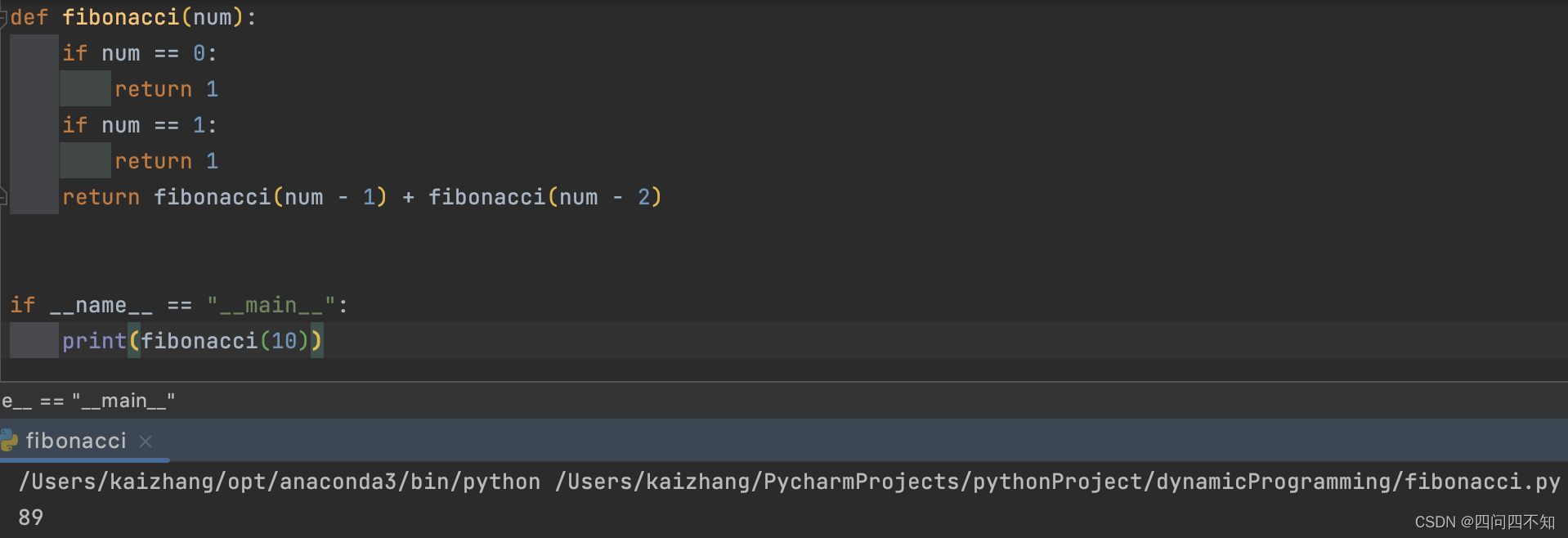
上述是以递归的方式实现的,然而递归方式存在以下几个缺点:
- 1)递归调用,占用空间大;
- 2)递归太深,容易发生栈溢出;
- 3)可能存在大量重复计算;
| 结果 | (n-1)项 | (n-2)项 |
|---|---|---|
| f(n) | f(n-1) | f(n-2) |
| … | … | … |
| f(5) | f(4) | f(3) |
| f(4) | f(3) | f(2) |
| f(3) | f(2) | f(1) |
| f(2) | f(1) | f(0) |
以上述表格为例,可以看到在求下一个递归结果时,计算了之前已经计算出来的结果,存在重复计算项。
如果采用动态规划的方式,那么可以节省计算,采用数组暂存之前已经计算出来的结果。如下,
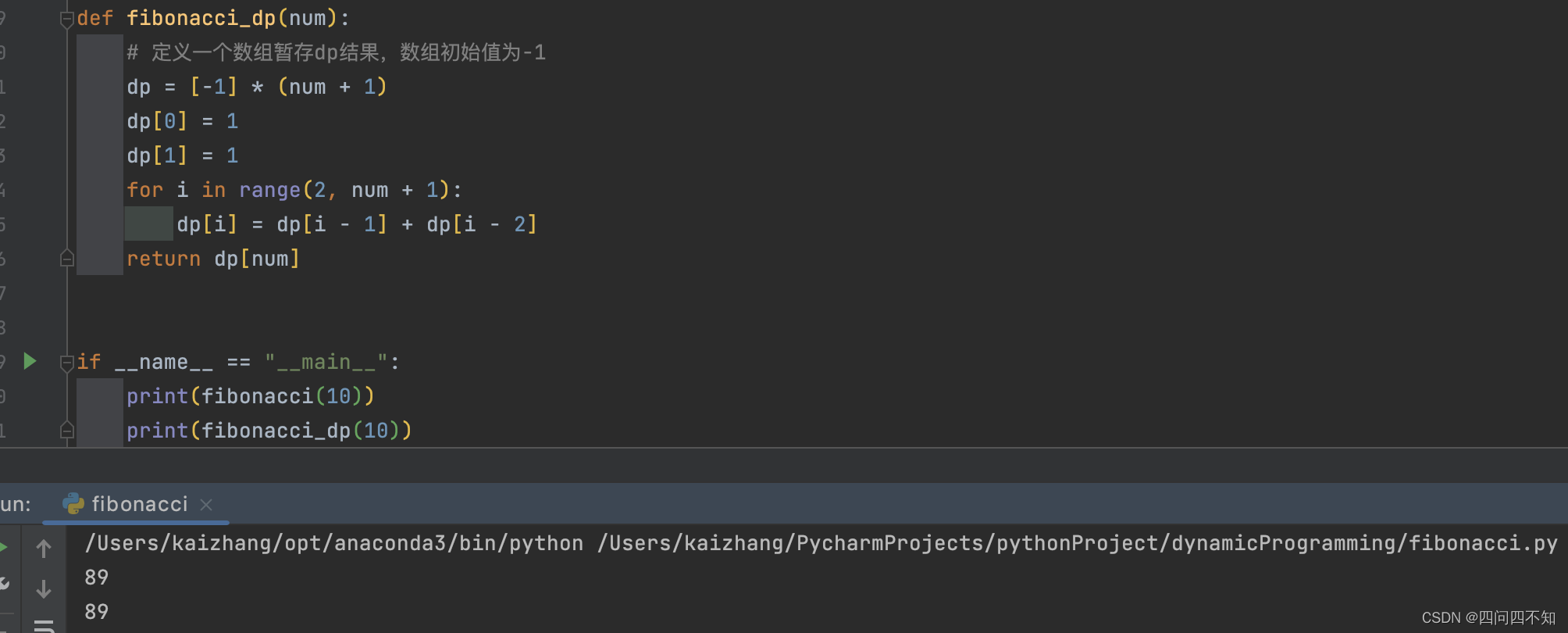
def fibonacci_dp(num):# 定义一个数组暂存dp结果,数组初始值为-1dp = [-1] * (num + 1)dp[0] = 1dp[1] = 1for i in range(2, num + 1):dp[i] = dp[i - 1] + dp[i - 2]return dp[num]if __name__ == "__main__":print(fibonacci_dp(10))
不同路径
上面的斐波那契数列是一维数组,较为简单,下面以二维数组为例。
题目描述
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?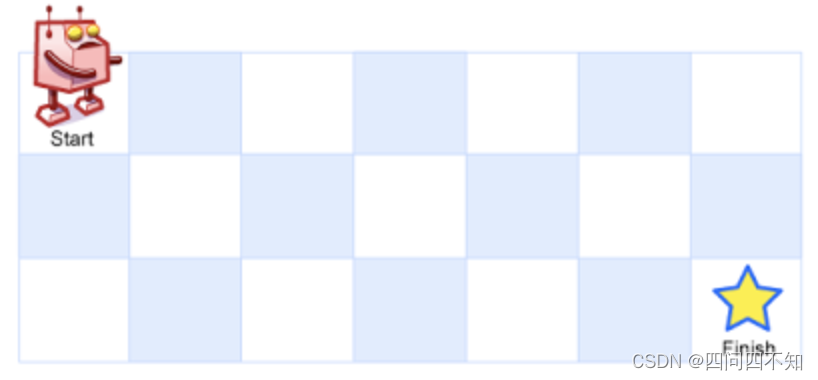
示例1: 输入:m = 3, n = 7 输出:28
示例2: 输入:m = 3, n = 2 输出:3
解释: 从左上角开始,总共有 3 条路径可以到达右下角。
1.向右 -> 向下 -> 向下
2.向下 -> 向下 -> 向右
3.向下 -> 向右 -> 向下
示例3:
输入:m = 7, n = 3 输出:28
示例4:
输入:m = 3, n = 3 输出:6
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10^9
python代码
class UniquePaths(object):def uniquePaths(self, m: int, n: int) -> int:""":type m: int:type n: int:rtype: int"""# 初始化一个二维数组dp = [[0] * n for _ in range(m)]for i in range(m):dp[i][0] = 1for j in range(n):dp[0][j] = 1for i in range(1, m):for j in range(1, n):dp[i][j] = dp[i - 1][j] + dp[i][j - 1]return dp[m - 1][n - 1]if __name__ == "__main__":demo = UniquePaths()print(demo.uniquePaths(7, 3))
最小路径和
题目描述
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:一个机器人每次只能向下或者向右移动一步。
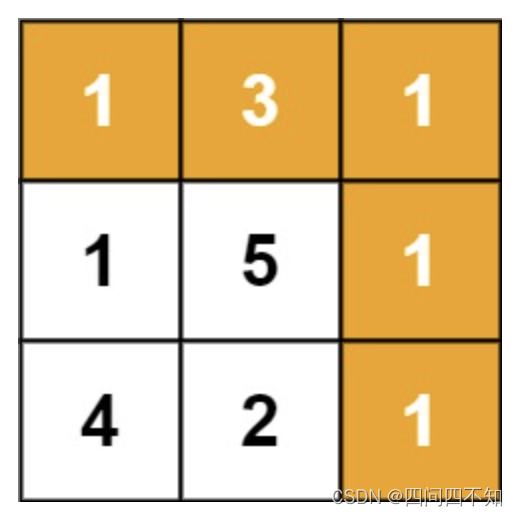
示例1:
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100
python代码
class MinPathSum(object):def minPathSum(self, grid):""":type grid: List[List[int]]:rtype: int"""row = len(grid)column = len(grid[0])# 定义dp[i][j]为到(i,j)处的最小路径和dp = [[0] * column for _ in range(row)]dp[0][0] = grid[0][0]# 第0行j列for j in range(1, column):dp[0][j] = dp[0][j - 1] + grid[0][j]# 第i行0列for i in range(1, row):dp[i][0] = dp[i - 1][0] + grid[i][0]# 非第0行或第0列for i in range(1, row):for j in range(1, column):dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]return dp[row - 1][column - 1]if __name__ == "__main__":demo = MinPathSum()grid = [[1, 3, 1], [1, 5, 1], [4, 2, 1]]print(demo.minPathSum(grid))

零钱兑换
题目描述
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
提示:
1 <= coins.length <= 12
1 <= coins[i] <= 231 - 1
0 <= amount <= 104
python代码
class CoinChange(object):def coinChange(self, coins: list[int], amount: int) -> int:""":type coins: List[int]:type amount: int:rtype: int"""# 状态转移方程dp(i) = min(dp(i-Cj)) + 1,Cj为货币面值"""i<0 忽略i==0 dp[0] = 0i==1 dp[1] = min(dp[1-1], dp[1-2], dp[1-5]) + 1 = 1i==2 dp[2] = min(dp[2-1], dp[2-2], dp[2-5]) + 1 = 1i==3 dp[3] = min(dp[3-1], dp[3-2], dp[3-5]) + 1 = 2i==4 dp[4] = min(dp[4-1], dp[4-2], dp[4-5]) + 1 = 2... ..."""dp = [0] * (amount + 1)dp[0] = 0for i in range(1, amount + 1):mini = int(1e9)for coin in coins:if i >= coin:res = dp[i - coin]if 0 <= res < mini:mini = resdp[i] = mini + 1 if mini < int(1e9) else -1if amount < 1:return 0return dp[amount]if __name__ == "__main__":demo = CoinChange()coins = [1, 2, 5]amount = 11print(demo.coinChange(coins, amount))
相关文章:

Python之动态规划
序言 最近在学习python语言,语言有通用性,此文记录复习动态规划并练习python语言。 动态规划(Dynamic Programming) 动态规划是运筹学的一个分支,是求解决策过程最优化的过程。20世纪50年代初,美国数学家…...

[ES]二基础 |
一、索引库操作 1、mapping属性 mapping是对索引库中文档的约束,常见的mapping属性包括: 1)type:字段数据类型,常见的简单类型有: ①字符串:text(可分词的文本)、keyword(精确值,…...

vscode vue3自定义自动补全
敲代码多了,发现重发动作很多,于是还是定义自动补全代码吧——懒是第一生产力! 1,Ctrl Shift P打开快捷命令行:找到下面这个 2,然后找到ts: 里面给了demo照着写就行 // "Print to conso…...

Spring Cloud + Spring Boot 项目搭建结构层次示例讲解
Spring Cloud Spring Boot 项目搭建结构层次示例讲解 Spring Cloud 项目搭建结构层次示例Spring Cloud示例: Spring Boot 项目搭建结构层次讲解Spring Boot 项目通常按照一种常见的架构模式组织,可以分为以下几个主要层次:当构建一个 Spring…...
使用cgroup工具对服务器某些/全部用户进行计算资源限制
使用cgroup工具对服务器某些/全部用户进行计算资源限制 主要介绍,如何对指定/所有用户进行资源限定(这里主要介绍cpu和内存占用限制),防止某些用户大量占用服务器计算资源,影响和挤占他人正常使用服务器。 安装cgrou…...
C#获取DataTable的前N行数据然后按指定字段排序
获取DataTable的前N行数据然后按指定字段排序 可以使用以下三种代码: 第一种:使用Linq DataTable dtLast dataTable.AsEnumerable().Take(count).OrderBy(dataRow > Convert.ToInt32(dataRow["Sequence"])).CopyToDataTable(); 第二种…...

Swift 中的动态成员查找
文章目录 前言基础介绍基础示例1. 定义一个动态成员访问类:2. 访问嵌套动态成员: 使用 KeyPath 的编译时安全性KeyPath 用法示例KeyPath 进阶使用示例1. 动态访问属性:2. 结合可选属性和 KeyPath:3. 动态 KeyPath 和字典ÿ…...

leetcode做题笔记102. 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。 思路一:递归 int** levelOrder(struct TreeNode* root, int* returnSize, int** returnColumnSizes){int** ans(int**)mal…...
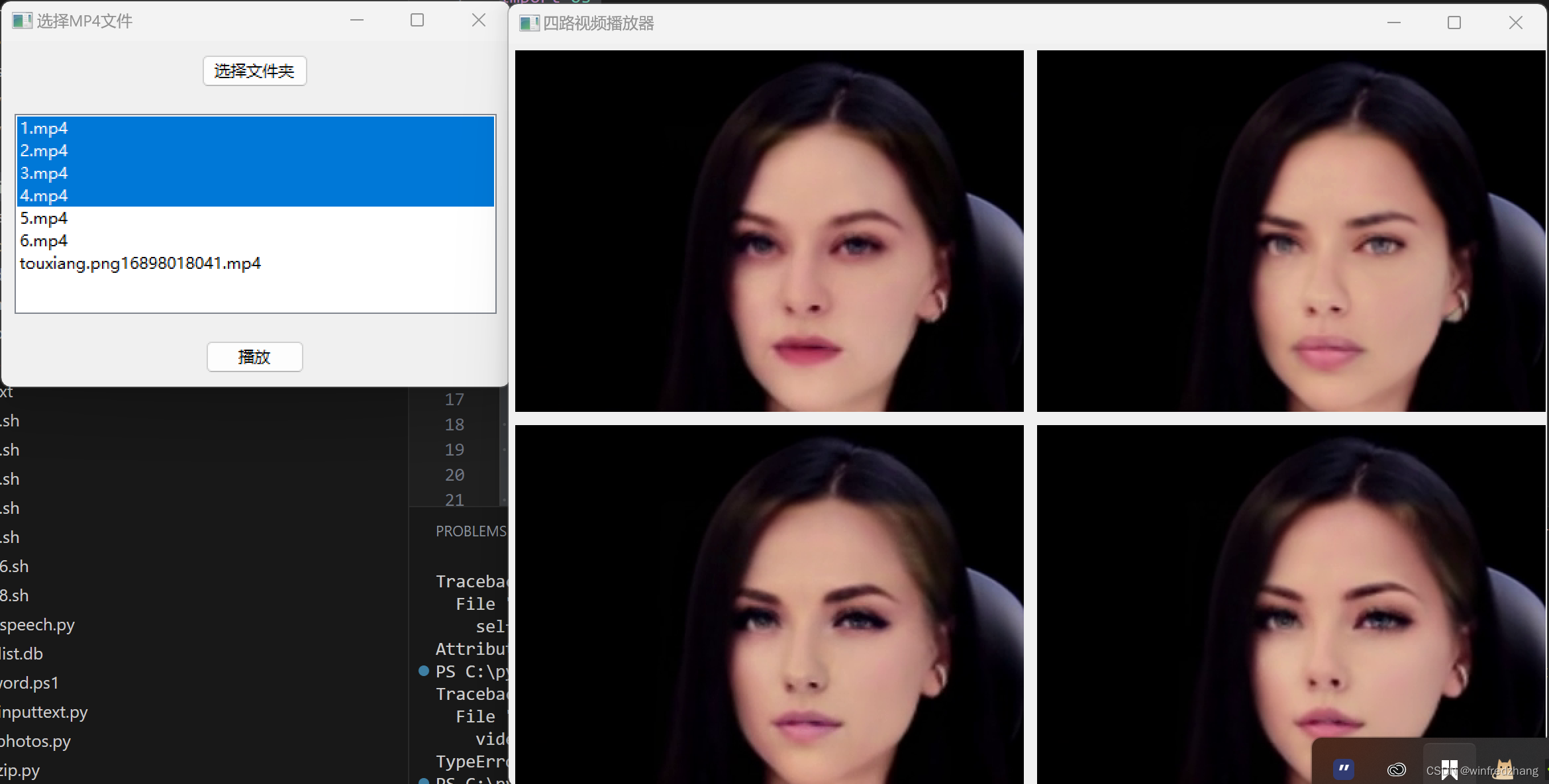
python编写四画面同时播放swap视频
当代技术让我们能够创建各种有趣和实用的应用程序。在本篇博客中,我们将探索一个基于wxPython和OpenCV的四路视频播放器应用程序。这个应用程序可以同时播放四个视频文件,并将它们显示在一个GUI界面中。 C:\pythoncode\new\smetimeplaymp4.py 准备工作…...

用XSIBackup为VMware ESXi打造完美备份方案
文章目录 VMware ESXi 备份方案引言XSIBackup安装步骤1. XSIBackup软件安装2. SSH连接3. 定位到xsibackup目录4. 修改文件权限5. 安装cron查看crontab列表6. 配置备份任务结论VMware ESXi 备份方案 引言 数据就像是我们的生命线,一旦丢失,可能会带来无法挽回的损失。对于那…...

React 项目中引入msal验证以及部分报错处理
功能实现 如何在React 项目中引入msal身份验证, 微软在官网有提供文档支持,文档包含示例和具体使用的教程,地址如下: https://learn.microsoft.com/zh-cn/azure/active-directory/develop/tutorial-v2-nodejs-webapp-msal 照着文…...

Unity3D 2021 使用 SharpZipLib 遇到的安卓打包 I18N 相关问题
在 Unity3D 中,使用 ICSharpCode.SharpZipLib.dll 来做压缩和解压缩,但打包安卓后遇到问题,原因是字符编码程序集被裁减掉了导致。 根据网上搜索,将 UnityEditor 对应目录下的 I18N开头的,比如 I18N.CJK.dll 等系列文…...
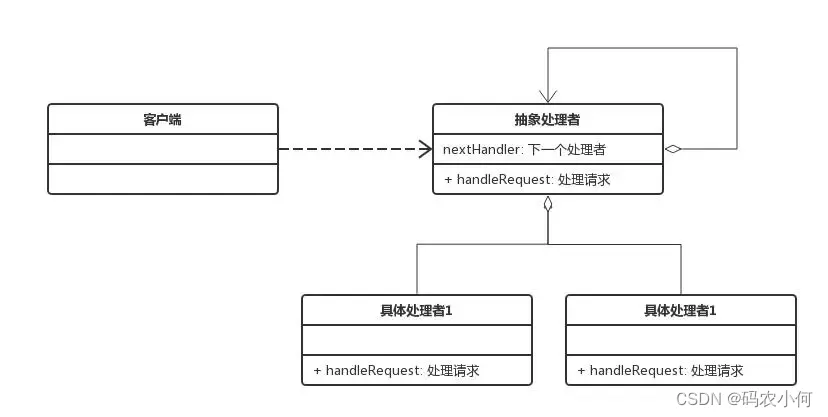
软件工程(十五) 行为型设计模式(一)
1、责任链模式 简要说明 通过多个对象处理的请求,减少请求的发送者与接收者之间的耦合。将接受对象链接起来,在链中传递请求,直到有一个对象处理这个请求。 速记关键字 传递职责 类图如下 由类图可以比较容易的看出来,其实就是自己关联自己,形成了一个链,并且自己有…...

【校招VIP】前端算法考点之快慢指针题型
考点介绍: 链表是校招面试里手撕代码出现频度比较高的题型,三线和中小厂会考察简单的链表反转,大厂会进一步考察复杂度和双指针问题,比如中间元素、是否存在环等。 『前端算法考点之快慢指针题型』相关题目及解析内容可点击文章末…...
Docker基础入门:容器数据卷与Dockerfile构建镜像(发布)
Docker基础入门:容器数据卷与Dockerfile构建镜像(发布) 一、docker容器数据卷1.1、使用docker容器数据卷1.2、具名挂载、匿名挂载1.3、如何确定是具名挂载还是匿名挂载 二、使用dockerfile2.1 初识Dockerfile2.2 Dockerfile构建过程2.3 Docke…...
从零开始搭建一台NAS服务器(Linux虚拟机))
部署问题集合(二十一)从零开始搭建一台NAS服务器(Linux虚拟机)
前言 因工作需要,需要从零通过虚拟机搭建一台NAS服务器,以此记录下来 步骤 1、创建虚拟机 通过VMWare创建一台新虚拟机,虚拟机内存和磁盘自定义,不过建议尽量大一点 2、服务器端配置 查看是否安装有NFS服务:rpm …...
Git小白入门——了解分布式版本管理和安装
Git是什么? Git是目前世界上最先进的分布式版本控制系统(没有之一) 什么是版本控制系统? 程序员开发过程中,对于每次开发对各种文件的修改、增加、删除,达到预期阶段的一个快照就叫做一个版本。 如果有一…...

芯科科技宣布推出下一代暨第三代无线开发平台,打造更智能、更高效的物联网
第三代平台中的人工智能/机器学习引擎可将性能提升100倍以上 Simplicity Studio 6软件开发工具包通过新的开发环境将开发人员带向第三代平台 中国,北京 - 2023年8月22日 – 致力于以安全、智能无线连接技术,建立更互联世界的全球领导厂商Silicon Labs&…...

无涯教程-Android - Intents/Filters
Android Intent 是要执行的操作的抽象描述。它可以与 startActivity 一起启动Activity,将 broadcastIntent 发送给任何BroadcastReceiver组件,并与 startService(Intent)或 bindService(Intent,ServiceConnection,int)与后台服务进…...
NFTScan 正式上线 Base NFTScan 浏览器和 NFT API 数据服务
2023 年 8 月 24 号,NFTScan 团队正式对外发布了 Base NFTScan 基础设施,将为 Base 生态的 NFT 开发者和用户提供简洁高效的 NFT 数据搜索查询服务。NFTScan 作为全球领先的 NFT 数据基础设施服务商,Base 是继 Bitcoin、Ethereum、BNBChain、…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...
