MATLAB图论合集(三)Dijkstra算法计算最短路径
本贴介绍最短路径的计算,实现方式为迪杰斯特拉算法;对于弗洛伊德算法,区别在于计算了所有结点之间的最短路径,考虑到MATLAB计算的便捷性,计算时只需要反复使用迪杰斯特拉即可,暂不介绍弗洛伊德的实现
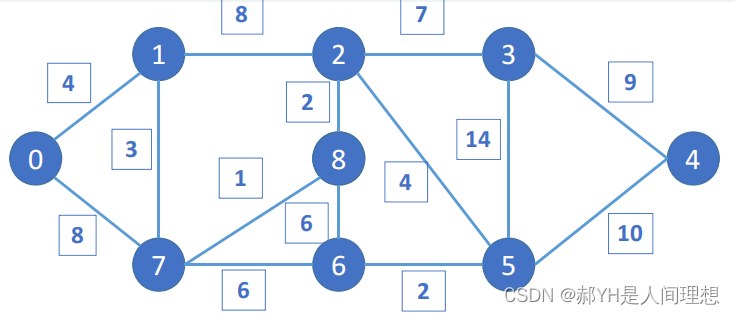
迪杰斯特拉算法的思想,通俗的归纳来说就是:从当前结点出发,寻找一个未与当前简历连接——且路径最小的点作为下一个寻找到的地址。有关结点是否建立连接,需要一个如下的矩阵来辅助记录。
 若还未建立连接,则将前驱标记为-1,距离记录为无穷~
若还未建立连接,则将前驱标记为-1,距离记录为无穷~
至于Distance内,存放的是起点到当前结点的最短距离,这一距离可能会不断更新,直到寻找到最短的路径为止~
实现的具体底代码:
- 第一种:
[P,d] = shortestpath(G, 9, 4)如上代码中,P表示的9与4节点之间最短路径经过的结点,而d保存的是最短路径值的总和~
- 第二种:
D = distances(G); D(1,2); D(9,4);如上代码中,D是一个存储了任意两结点之间最短路径的矩阵,通过索引访问的方式,即可求出任意两点的最短路径~
此外,如下是计算求出指定节点指定距离内部的全部结点的实现方式:
[nodeIDs,dist] = nearest(G, 2, 10); 注意,上述几个函数从2017a版本后才能全部使用
如下是创建图并计算图的具体实现方式:
s = [9 9 1 1 2 2 2 7 7 6 6 5 5 4];
t = [1 7 7 2 8 3 5 8 6 8 5 3 4 3];
w = [4 8 3 8 2 7 4 1 6 6 2 14 10 9];
G = graph(s,t,w);plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2) set( gca, 'XTick', [], 'YTick', [] );[P,d] = shortestpath(G, 9, 4);myplot = plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2);
highlight(myplot, P, 'EdgeColor', 'g') ; 结果如下,绿色即为最短路径:
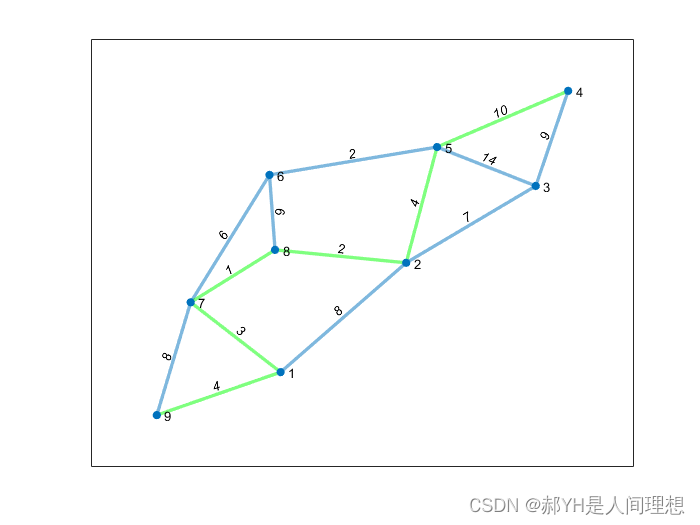
相关文章:

MATLAB图论合集(三)Dijkstra算法计算最短路径
本贴介绍最短路径的计算,实现方式为迪杰斯特拉算法;对于弗洛伊德算法,区别在于计算了所有结点之间的最短路径,考虑到MATLAB计算的便捷性,计算时只需要反复使用迪杰斯特拉即可,暂不介绍弗洛伊德的实现 迪杰斯…...

MySQL 8.0.xx 版本解决group by分组的问题
因为版本升级5.7版本以下是没有这个问题的,8.0版本以上会出现分组问题 1055 - Expression #1 of SELECT list is not in GROUP BY clause and contains nonaggregated column test1.sys_t.id which is not functionally dependent on columns in GROUP BY clause; t…...
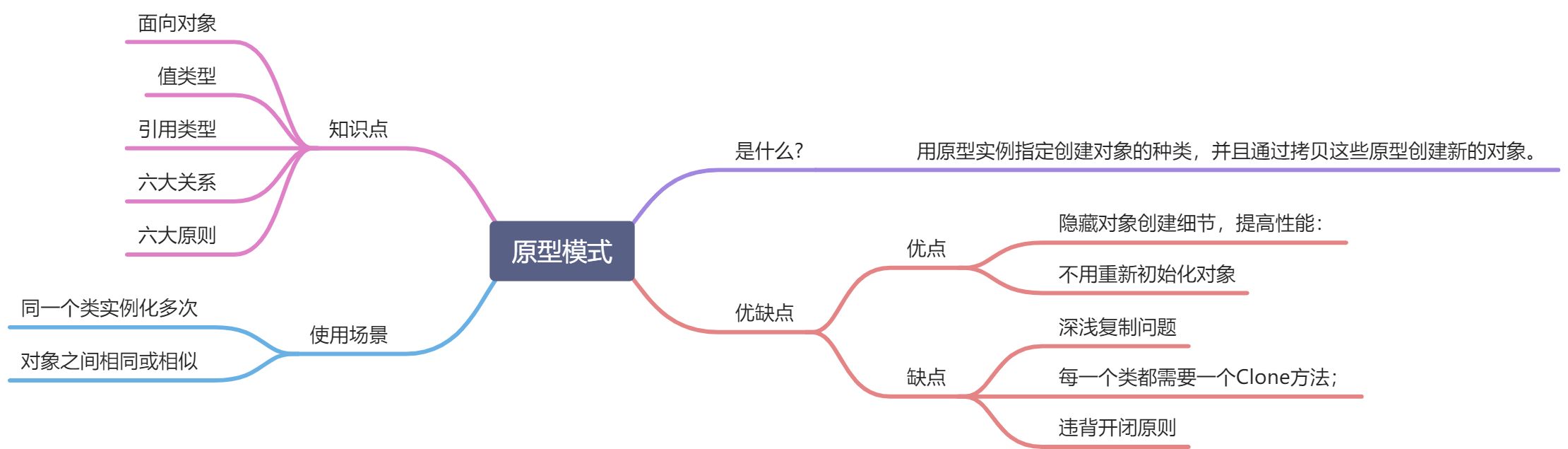
设计模式—原型模式(Prototype)
目录 一、什么是原型模式? 二、原型模式具有什么优缺点吗? 三、有什么缺点? 四、什么时候用原型模式? 五、代码展示 ①、简历代码初步实现 ②、原型模式 ③、简历的原型实现 ④、深复制 ⑤、浅复制 一、什么是原型模式&…...
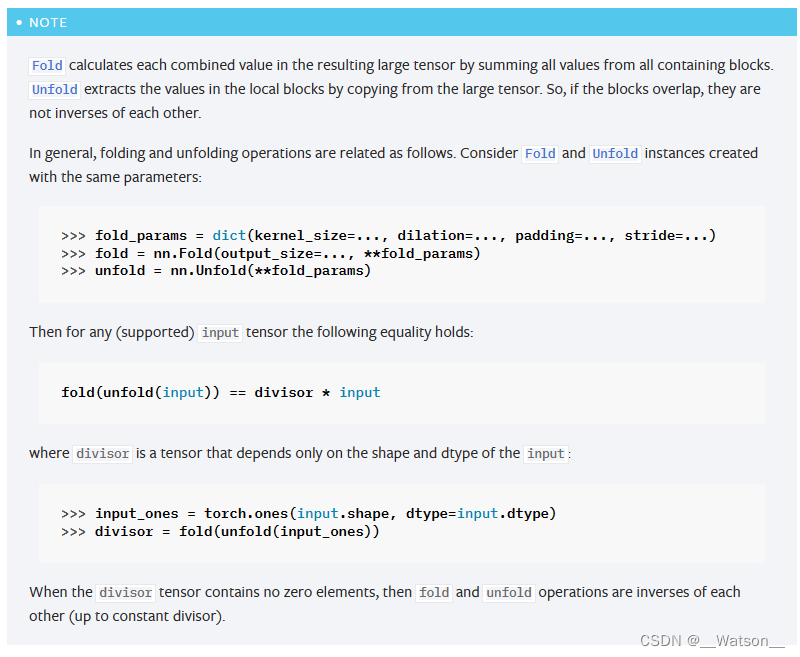
【pytorch】Unfold和Fold的互逆操作
1. 参数定义 Unfold https://pytorch.org/docs/stable/generated/torch.nn.Unfold.html#torch.nn.Unfold Fold https://pytorch.org/docs/stable/generated/torch.nn.Fold.html#torch.nn.Fold 注意:参数当中的padding是在四周边补零,而当fold后的尺寸…...

【AI】《动手学-深度学习-PyTorch版》笔记(二十一):目标检测
AI学习目录汇总 1、简述 通过前面的学习,已经了解了图像分类模型的原理及实现。图像分类是假定图像中只有一个目标,算法上是对整个图像做的分类。 下面我们来学习“目标检测”,即从一张图像中找出需要的目标,并标记出位置。 2、边界框 边界框:bounding box,就是一个方…...
畅捷通T+用户中locked勒索病毒后该怎么办?勒索病毒解密数据恢复
Locked勒索病毒是一种近年来在全球范围内引起广泛关注的网络安全威胁程序。它是一种加密货币劫持病毒,专门用于加密用户的数据并要求其支付赎金。Locked勒索病毒通过攻击各种系统漏洞和网络薄弱环节,使用户计算机受到感染并被加密锁定时,无法…...
神仙般的css动画参考网址,使用animate.css
Animate.css | A cross-browser library of CSS animations.Animate.css is a library of ready-to-use, cross-browser animations for you to use in your projects. Great for emphasis, home pages, sliders, and attention-guiding hints.https://animate.style/这里面有很…...

江西抚州新能源汽车3d扫描零部件逆向抄数测量改装-CASAIM中科广电
汽车改装除了在外观方面越来越受到消费者的青睐,在性能和实用性提升上面的需求也是日趋增多,能快速有效地对客户指定汽车零部件进行一个改装,是每一个汽车改装企业和工程师的追求,也是未来消费者个性化差异化的要求。下面CASAIM中…...
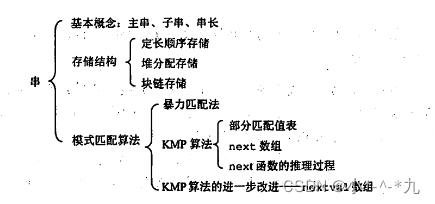
数据结构学习 --4 串
数据结构学习 --1 绪论 数据结构学习 --2 线性表 数据结构学习 --3 栈,队列和数组 数据结构学习 --4 串 数据结构学习 --5 树和二叉树 数据结构学习 --6 图 数据结构学习 --7 查找 数据结构学习 --8 排序 本人学习记录使用 希望对大家帮助 不当之处希望大家帮忙纠正…...

探索Kotlin K2编译器和Java编译器的功能和能力
文章首发地址 Kotlin K2编译器是Kotlin语言的编译器,负责将Kotlin源代码转换为Java字节码或者其他目标平台的代码。K2编译器是Kotlin语言的核心组件之一,它的主要功能是将Kotlin代码编译为可在JVM上运行的字节码。 K2编译器快速介绍 编译过程ÿ…...

如何安装chromadb
下载最新版本的python3.10 因为chromadb需要sqlite3的最小版本是3.35.0 使用如下命令安装 pip install chromadb 安装完毕后在python3的命令行窗口输入 import chromadb 如果不报错代表成功,如果报错sqlite3的最小版本是3.35.0,使用如下方式解决 …...

vue实现把字符串中的所有@内容,替换成带标签的
前言: 目前有个需求是,要把输入框里面的还有姓名高亮。 要求: 1、必须用 v-html ,带标签的给他渲染 2、把字符串中的全部查找出来,替换掉,注意要过滤已经替换好的,不然就是无限循环了 实现方法:…...

「MySQL-00」MySQL在Linux上的安装、登录与删除
目录 一、安装MySQL 0. 安装前请先执行一遍删除操作,把预装或残留的MySQL删除掉 1. 安装yum源 (解决了在哪里找MySQL的问题) 2. 安装哪个版本的MySQL 二、启动和登录MySQL 三、删除MySQL / MariaDB 安装与卸载前,建议先将用户切换…...

8月29-31日上课内容 第五章
第一章...

数据库导出工具
之前根据数据库升级需求,需要导出旧版本数据(sqlserver 6.5),利用c# winfrom写了一个小工具,导出数据。 →→→→→多了不说,少了不唠。进入正题→→→→ 连接数据库:输入数据库信息 连接成功…...
ChatGPT 制作可视化柱形图突出显示第1名与最后1名
对比分析柱形图的用法。在图表中显示最大值与最小值。 像这样的动态图表的展示只需要给ChatGPT,AIGC,OpenAI 发送一个指令就可以了, 人工智能会快速的写出HTML与JS代码来实现。 请使用HTML,JS,Echarts完成一个对比分析柱形图,在图表中突出显示第1名和最后1名用单独一种不…...

前端学习记录~2023.8.10~JavaScript重难点实例精讲~第6章 Ajax
第 6 章 Ajax 前言6.1 Ajax的基本原理及执行过程6.1.1 XMLHttpRequest对象(1)XMLHttpRequest对象的函数(2)XMLHttpRequest对象的属性 6.1.2 XMLHttpRequest对象生命周期(1)创建XMLHttpRequest对象ÿ…...
)
2023年Java核心技术第九篇(篇篇万字精讲)
目录 十七 . 并发相关基础概念 17.1 线程安全 17.2 保证线程安全的两个方法 17.2.1 封装 17.2.2 不可变 17.2.2.1 final 和 immutable解释 17.3 线程安全的基本特性 17.3.1 原子性(Atomicity) 17.3.2 可见性(Visibility) 17.3.2.1…...

C#上位机中的单例应用思考
文章目录 一、前言二、上位机单例应用场景2.1 上位机2.2 单例及其应用2.3 上位机中的应用2.3.1 用户登录信息2.3.2 配置文件2.3.3 数据连接池 2.4 一个应用场景的思考 三、总结 一、前言 之前写过一篇关于单例的文——C#中单例模式的实现,讲了讲单例是什么以及在C#…...

Python分享之redis
String 操作 redis中的String在在内存中按照一个name对应一个value来存储 set() #在Redis中设置值,默认不存在则创建,存在则修改 r.set(name, zhangsan) 参数: set(name, value, exNone, pxNone, nxFalse, xxFalse) exÿ…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
