2023年高教社杯数学建模思路 - 案例:感知机原理剖析及实现
文章目录
- 1 感知机的直观理解
- 2 感知机的数学角度
- 3 代码实现
- 4 建模资料
# 0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 感知机的直观理解
感知机应该属于机器学习算法中最简单的一种算法,其原理可以看下图:
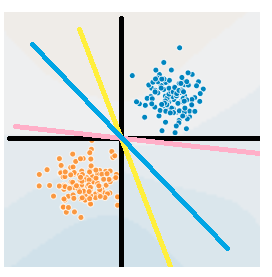
比如说我们有一个坐标轴(图中的黑色线),横的为x1轴,竖的x2轴。图中的每一个点都是由(x1,x2)决定的。如果我们将这张图应用在判断零件是否合格上,x1表示零件长度,x2表示零件质量,坐标轴表示零件的均值长度和均值重量,并且蓝色的为合格产品,黄色为劣质产品,需要剔除。那么很显然如果零件的长度和重量都大于均值,说明这个零件是合格的。也就是在第一象限的所有蓝色点。反之如果两项都小于均值,就是劣质的,比如在第三象限的黄色点。
在预测上很简单,拿到一个新的零件,我们测出它的长度x1,质量x2,如果两项都大于均值,说明零件合格。这就是我们人的人工智能。
那么程序怎么知道长度重量都大于均值的零件就是合格的呢?
或者说
它是怎么学会这个规则的呢?
程序拿到手的是当前图里所有点的信息以及标签,也就是说它知道所有样本x的坐标为(x1, x2),同时它属于蓝色或黄色。对于目前手里的这些点,要是能找到一条直线把它们分开就好了,这样我拿到一个新的零件,知道了它的质量和重量,我就可以判断它在线的哪一侧,就可以知道它可能属于好的或坏的零件了。例如图里的黄、蓝、粉三条线,都可以完美地把当前的两种情况划分开。甚至x1坐标轴或x2坐标轴都能成为一个划分直线(这两个直线均能把所有点正确地分开)。
读者也看到了,对于图中的两堆点,我们有无数条直线可以将其划分开,事实上我们不光要能划分当前的点,当新来的点进来是,也要能很好地将其划分,所以哪条线最好呢?
怎样一条直线属于最佳的划分直线?实际上感知机无法找到一条最佳的直线,它找到的可能是图中所有画出来的线,只要能把所有的点都分开就好了。
得出结论:
如果一条直线能够不分错一个点,那就是一条好的直线
进一步来说:
如果我们把所有分错的点和直线的距离求和,让这段求和的举例最小(最好是0,这样就表示没有分错的点了),这条直线就是我们要找的。
2 感知机的数学角度
首先我们确定一下终极目标:甭管找最佳划分直线啥中间乱七八糟的步骤,反正最后生成一个函数f(x),当我们把新的一个数据x扔进函数以后,它会预测告诉我这是蓝的还是黄的,多简单啊。所以我们不要去考虑中间过程,先把结果定了。
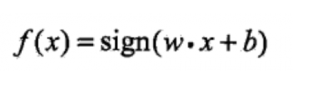
瞧,f(x)不是出来了嘛,sign是啥?wx+b是啥?别着急,我们再看一下sigin函数是什么。
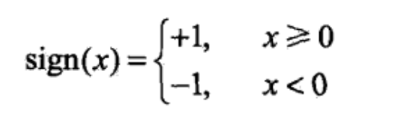
sign好像很简单,当x大于等于0,sign输出1,否则输出-1。那么往前递归一下,wx+b如果大于等于0,f(x)就等于1,反之f(x)等于-1。
那么wx+b是啥?
它就是那条最优的直线。我们把这个公式放在二维情况下看,二维中的直线是这样定义的:y=ax+b。在二维中,w就是a,b还是b。所以wx+b是一条直线(比如说本文最开始那张图中的蓝线)。如果新的点x在蓝线左侧,那么wx+b<0,再经过sign,最后f输出-1,如果在右侧,输出1。等等,好像有点说不通,把情况等价到二维平面中,y=ax+b,只要点在x轴上方,甭管点在线的左侧右侧,最后结果都是大于0啊,这个值得正负跟线有啥关系?emmm….其实wx+b和ax+b表现直线的形式一样,但是又稍有差别。我们把最前头的图逆时针旋转45度,蓝线是不是变成x轴了?哈哈这样是不是原先蓝线的右侧变成了x轴的上方了?其实感知机在计算wx+b这条线的时候,已经在暗地里进行了转换,使得用于划分的直线变成x轴,左右侧分别为x轴的上方和下方,也就成了正和负。
那么,为啥是wx+b,而不叫ax+b?
在本文中使用零件作为例子,上文使用了长度和重量(x1,x2)来表示一个零件的属性,所以一个二维平面就足够,那么如果零件的品质和色泽也有关系呢?那就得加一个x3表示色泽,样本的属性就变成了(x1,x2,x3),变成三维了。wx+b并不是只用于二维情况,在三维这种情况下,仍然可以使用这个公式。所以wx+b与ax+b只是在二维上近似一致,实际上是不同的东西。在三维中wx+b是啥?我们想象屋子里一个角落有蓝点,一个角落有黄点,还用一条直线的话,显然是不够的,需要一个平面!所以在三维中,wx+b是一个平面!至于为什么,后文会详细说明。四维呢?emmm…好像没法描述是个什么东西可以把四维空间分开,但是对于四维来说,应该会存在一个东西像一把刀一样把四维空间切成两半。能切成两半,应该是一个对于四维来说是个平面的东西,就像对于三维来说切割它的是一个二维的平面,二维来说是一个一维的平面。总之四维中wx+b可以表示为一个相对于四维来说是个平面的东西,然后把四维空间一切为二,我们给它取名叫超平面。由此引申,在高维空间中,wx+b是一个划分超平面,这也就是它正式的名字。
正式来说:
wx+b是一个n维空间中的超平面S,其中w是超平面的法向量,b是超平面的截距,这个超平面将特征空间划分成两部分,位于两部分的点分别被分为正负两类,所以,超平面S称为分离超平面。
细节:
w是超平面的法向量:对于一个平面来说w就是这么定义的,是数学知识,可以谷歌补习一下
b是超平面的截距:可以按照二维中的ax+b理解
特征空间:也就是整个n维空间,样本的每个属性都叫一个特征,特征空间的意思是在这个空间中可以找到样本所有的属性组合

我们从最初的要求有个f(x),引申到能只输出1和-1的sign(x),再到现在的wx+b,看起来越来越简单了,只要能找到最合适的wx+b,就能完成感知机的搭建了。前文说过,让误分类的点距离和最大化来找这个超平面,首先我们要放出单独计算一个点与超平面之间距离的公式,这样才能将所有的点的距离公式求出来对不?

先看wx+b,在二维空间中,我们可以认为它是一条直线,同时因为做过转换,整张图旋转后wx+b是x轴,那么所有点到x轴的距离其实就是wx+b的值对不?当然了,考虑到x轴下方的点,得加上绝对值->|wx+b|,求所有误分类点的距离和,也就是求|wx+b|的总和,让它最小化。很简单啊,把w和b等比例缩小就好啦,比如说w改为0.5w,b改为0.5b,线还是那条线,但是值缩小两倍啦!你还不满意?我可以接着缩!缩到0去!所以啊,我们要加点约束,让整个式子除以w的模长。啥意思?就是w不管怎么样,要除以它的单位长度。如果我w和b等比例缩小,那||w||也会等比例缩小,值一动不动,很稳。没有除以模长之前,|wx+b|叫函数间隔,除模长之后叫几何间隔,几何间隔可以认为是物理意义上的实际长度,管你怎么放大缩小,你物理距离就那样,不可能改个数就变。在机器学习中求距离时,通常是使用几何间隔的,否则无法求出解。

对于误分类的数据,例如实际应该属于蓝色的点(线的右侧,y>0),但实际上预测出来是在左侧(wx+b<0),那就是分错了,结果是负,这时候再加个符号,结果就是正了,再除以w的模长,就是单个误分类的点到超平面的举例。举例总和就是所有误分类的点相加。
上图最后说不考虑除以模长,就变成了函数间隔,为什么可以这么做呢?不考虑wb等比例缩小这件事了吗?上文说的是错的吗?
有一种解释是这样说的:感知机是误分类驱动的算法,它的终极目标是没有误分类的点,如果没有误分类的点,总和距离就变成了0,w和b值怎样都没用。所以几何间隔和函数间隔在感知机的应用上没有差别,为了计算简单,使用函数间隔。

以上是损失函数的正式定义,在求得划分超平面的终极目标就是让损失函数最小化,如果是0的话就相当完美了。

感知机使用梯度下降方法求得w和b的最优解,从而得到划分超平面wx+b,关于梯度下降及其中的步长受篇幅所限可以自行谷歌。
3 代码实现
#coding=utf-8
#Author:Dodo
#Date:2018-11-15
#Email:lvtengchao@pku.edu.cn
'''
数据集:Mnist
训练集数量:60000
测试集数量:10000
------------------------------
运行结果:
正确率:81.72%(二分类)
运行时长:78.6s
'''
import numpy as np
import time
def loadData(fileName):'''加载Mnist数据集:param fileName:要加载的数据集路径:return: list形式的数据集及标记'''print('start to read data')# 存放数据及标记的listdataArr = []; labelArr = []# 打开文件fr = open(fileName, 'r')# 将文件按行读取for line in fr.readlines():# 对每一行数据按切割福','进行切割,返回字段列表curLine = line.strip().split(',')# Mnsit有0-9是个标记,由于是二分类任务,所以将>=5的作为1,<5为-1if int(curLine[0]) >= 5:labelArr.append(1)else:labelArr.append(-1)#存放标记#[int(num) for num in curLine[1:]] -> 遍历每一行中除了以第一哥元素(标记)外将所有元素转换成int类型#[int(num)/255 for num in curLine[1:]] -> 将所有数据除255归一化(非必须步骤,可以不归一化)dataArr.append([int(num)/255 for num in curLine[1:]])#返回data和labelreturn dataArr, labelArr
def perceptron(dataArr, labelArr, iter=50):'''感知器训练过程:param dataArr:训练集的数据 (list):param labelArr: 训练集的标签(list):param iter: 迭代次数,默认50:return: 训练好的w和b'''print('start to trans')#将数据转换成矩阵形式(在机器学习中因为通常都是向量的运算,转换称矩阵形式方便运算)#转换后的数据中每一个样本的向量都是横向的dataMat = np.mat(dataArr)#将标签转换成矩阵,之后转置(.T为转置)。#转置是因为在运算中需要单独取label中的某一个元素,如果是1xN的矩阵的话,无法用label[i]的方式读取#对于只有1xN的label可以不转换成矩阵,直接label[i]即可,这里转换是为了格式上的统一labelMat = np.mat(labelArr).T#获取数据矩阵的大小,为m*nm, n = np.shape(dataMat)#创建初始权重w,初始值全为0。#np.shape(dataMat)的返回值为m,n -> np.shape(dataMat)[1])的值即为n,与#样本长度保持一致w = np.zeros((1, np.shape(dataMat)[1]))#初始化偏置b为0b = 0#初始化步长,也就是梯度下降过程中的n,控制梯度下降速率h = 0.0001#进行iter次迭代计算for k in range(iter):#对于每一个样本进行梯度下降#李航书中在2.3.1开头部分使用的梯度下降,是全部样本都算一遍以后,统一#进行一次梯度下降#在2.3.1的后半部分可以看到(例如公式2.6 2.7),求和符号没有了,此时用#的是随机梯度下降,即计算一个样本就针对该样本进行一次梯度下降。#两者的差异各有千秋,但较为常用的是随机梯度下降。for i in range(m):#获取当前样本的向量xi = dataMat[i]#获取当前样本所对应的标签yi = labelMat[i]#判断是否是误分类样本#误分类样本特诊为: -yi(w*xi+b)>=0,详细可参考书中2.2.2小节#在书的公式中写的是>0,实际上如果=0,说明改点在超平面上,也是不正确的if -1 * yi * (w * xi.T + b) >= 0:#对于误分类样本,进行梯度下降,更新w和bw = w + h * yi * xib = b + h * yi#打印训练进度print('Round %d:%d training' % (k, iter))#返回训练完的w、breturn w, b
def test(dataArr, labelArr, w, b):'''测试准确率:param dataArr:测试集:param labelArr: 测试集标签:param w: 训练获得的权重w:param b: 训练获得的偏置b:return: 正确率'''print('start to test')#将数据集转换为矩阵形式方便运算dataMat = np.mat(dataArr)#将label转换为矩阵并转置,详细信息参考上文perceptron中#对于这部分的解说labelMat = np.mat(labelArr).T#获取测试数据集矩阵的大小m, n = np.shape(dataMat)#错误样本数计数errorCnt = 0#遍历所有测试样本for i in range(m):#获得单个样本向量xi = dataMat[i]#获得该样本标记yi = labelMat[i]#获得运算结果result = -1 * yi * (w * xi.T + b)#如果-yi(w*xi+b)>=0,说明该样本被误分类,错误样本数加一if result >= 0: errorCnt += 1#正确率 = 1 - (样本分类错误数 / 样本总数)accruRate = 1 - (errorCnt / m)#返回正确率return accruRate
if __name__ == '__main__':#获取当前时间#在文末同样获取当前时间,两时间差即为程序运行时间start = time.time()#获取训练集及标签trainData, trainLabel = loadData('../Mnist/mnist_train.csv')#获取测试集及标签testData, testLabel = loadData('../Mnist/mnist_test.csv')#训练获得权重w, b = perceptron(trainData, trainLabel, iter = 30)#进行测试,获得正确率accruRate = test(testData, testLabel, w, b)#获取当前时间,作为结束时间end = time.time()#显示正确率print('accuracy rate is:', accruRate)#显示用时时长print('time span:', end - start)
4 建模资料
资料分享: 最强建模资料


相关文章:

2023年高教社杯数学建模思路 - 案例:感知机原理剖析及实现
文章目录 1 感知机的直观理解2 感知机的数学角度3 代码实现 4 建模资料 # 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 感知机的直观理解 感知机应该属于机器学习算法中最简单的一种算法,其…...
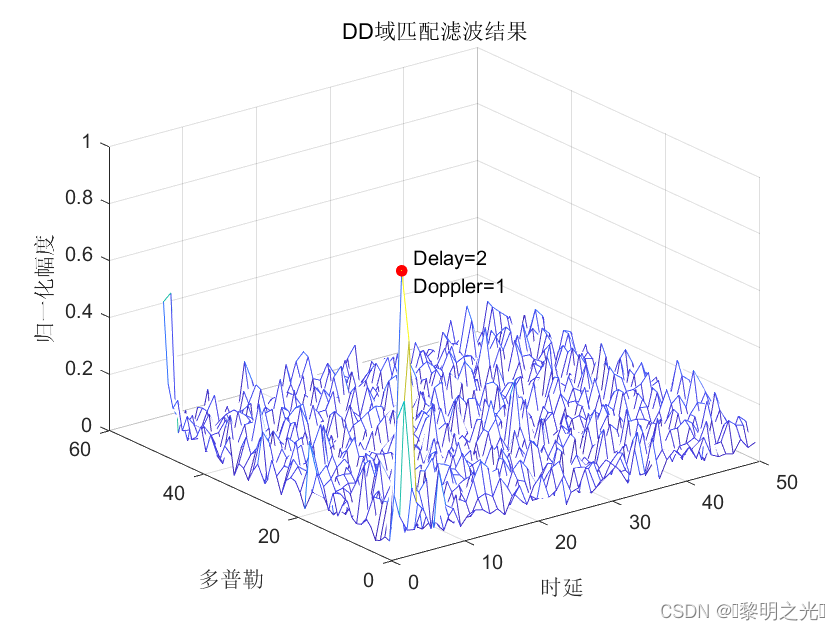
OTFS-ISAC雷达部分最新进展(含matlab仿真+USRP验证)
OTFS基带参数设置 我将使用带宽为80MHz的OTFS波形进行设计,对应参数如下: matlab Tx仿真 Tx导频Tx功率密度谱 帧结构我使用的是经典嵌入导频帧结构,Tx信号波形的带宽从右图可以看出约为80Mhz USRP验证 测试环境 无人机位于1m处 Rx导频Rx…...
Cell | 超深度宏基因组!复原消失的肠道微生物
期刊:Cell IF:64.5 (Q1) 发表时间:2023.6 研究背景 不同的生活方式会影响微生物组组成,但目前微生物组的研究严重偏向于西方工业化人群,其中工业化人群的特点是微生物群多样性较低。为了理解工…...

Centos7 设置代理方法
针对上面变量的设置方法: 1、在/etc/profile文件 2、在~/.bashrc 3、在~/.zshrc 4、在/etc/profile.d/文件夹下新建一个文件xxx.sh 写入如下配置: export proxy"http://192.168.5.14:8118" export http_proxy$proxy export https_proxy$pro…...
)
Android versions (Android 版本)
Android versions (Android 版本) All Android releases https://developer.android.com/about/versions Android 1.0 G1 Android 1.5 Cupcake Android 1.6 Donut Android 2.0 Eclair Android 2.2 Froyo Android 2.3 Gingerbread Android 3.0 Honeycomb Android 4.0 Ic…...
LNMP 平台搭建(四十)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 搭建LNMP 一、安装Nginx 二、安装Mysql 三、安装PHP 四、部署应用 前言 LNMP平台指的是将Linux、Nginx、MySQL和PHP(或者其他的编程语言,如…...

pcie 6.0/7.0相对pcie 5.0的变化有哪些?
引言 话说,小编在CSDN博客跟客服机器人聊天,突然看到有个搜索热搜“pcie最全科普贴”。小编有点似曾相识呀,我就好奇点击了一下,没想到几年前写的帖子在CSDN又火了一把。 说到这里,顺带给自己打个广告哈~ …...

百度Apollo:自动驾驶技术的未来应用之路
文章目录 前言一、城市交通二、出行体验三、环境保护四、未来前景总结 前言 随着科技的不断进步,自动驾驶技术正逐渐成为现实,颠覆着我们的出行方式。作为中国领先的自动驾驶平台,百度Apollo以其卓越的技术和开放的合作精神,正在…...

C++之std::distance应用实例(一百八十八)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

中国建筑出版传媒许少辉八一新书乡村振兴战略下传统村落文化旅游设计日
中国建筑出版传媒许少辉八一新书乡村振兴战略下传统村落文化旅游设计日...
基于java Swing 和 mysql实现的购物管理系统(源码+数据库+说明文档+运行指导视频)
一、项目简介 本项目是一套基于java Swing 和 mysql实现的购物管理系统,主要针对计算机相关专业的正在做毕设的学生与需要项目实战练习的Java学习者。 包含:项目源码、项目文档、数据库脚本等,该项目附带全部源码可作为毕设使用。 项目都经过…...

2023.9 - java - static 关键字
static关键字主要和Java的内存管理有关。我们可以将static关键字与变量,方法,代码块一起使用。static关键字属于该类,而不是该类的实例。 static关键字可以修饰: 变量(也称为类变量)方法(也称…...

SpringCloud学习笔记(十二)_Zipkin全链路监控
Zipkin是SpringCloud官方推荐的一款分布式链路监控的组件,使用它我们可以得知每一个请求所经过的节点以及耗时等信息,并且它对代码无任何侵入,我们先来看一下Zipkin给我们提供的UI界面都是提供了哪些信息。 如何使用Zipkin 虽然在SpringBoot…...
Java 多线程系列Ⅱ(线程安全)
线程安全 一、线程不安全线程不安全的原因: 二、线程不安全案例与解决方案1、修改共享资源synchronized 使用synchronized 特性 2、内存可见性Java内存模型(JMM)内存可见性问题 3、指令重排列4、synchronized 和 volatile5、拓展知识…...

const用法详解
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、const用法详解二、使用步骤 1.引入库2.读入数据总结 前言 提示:这里可以添加本文要记录的大概内容: 例如:随着人工智能…...
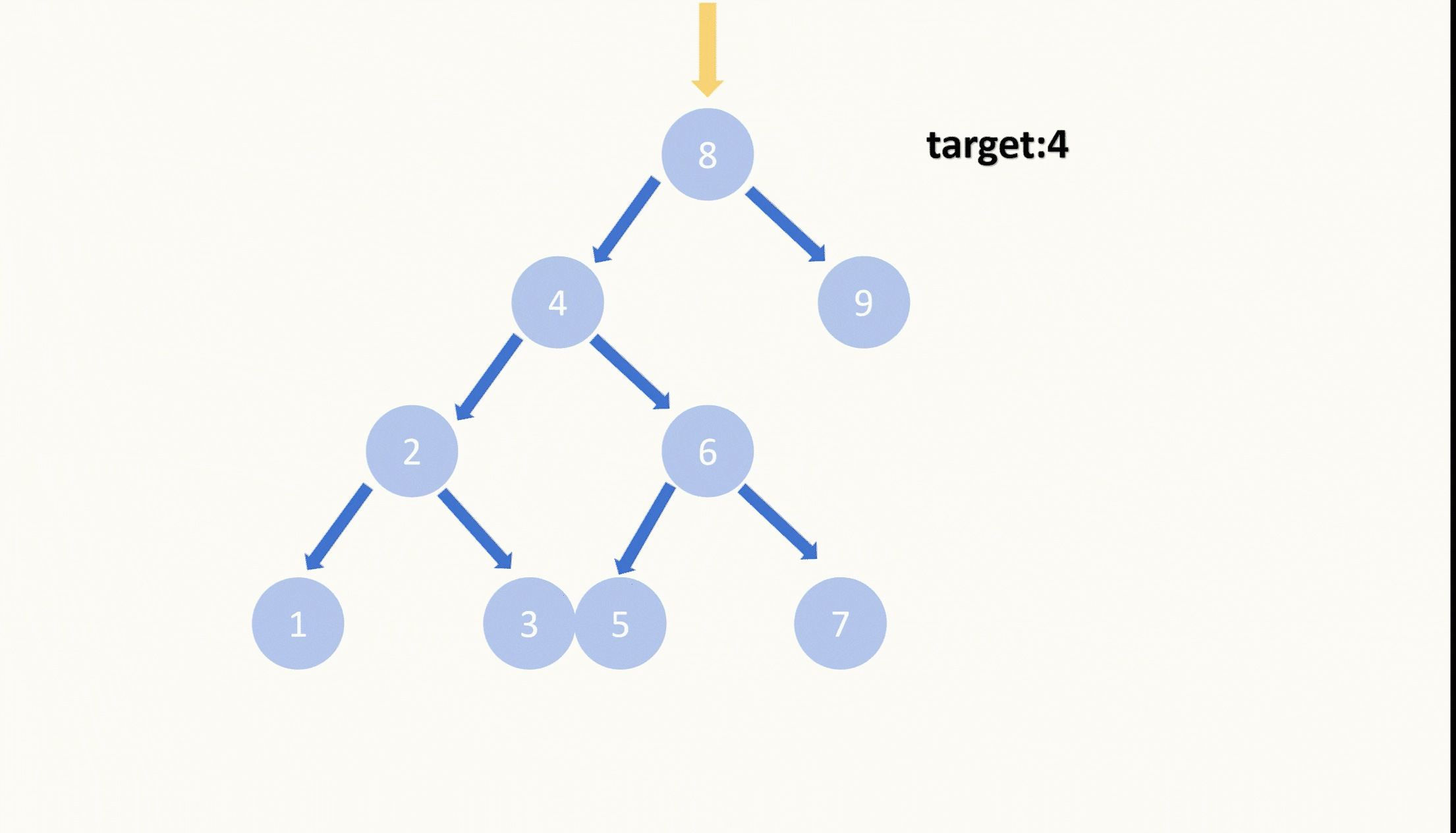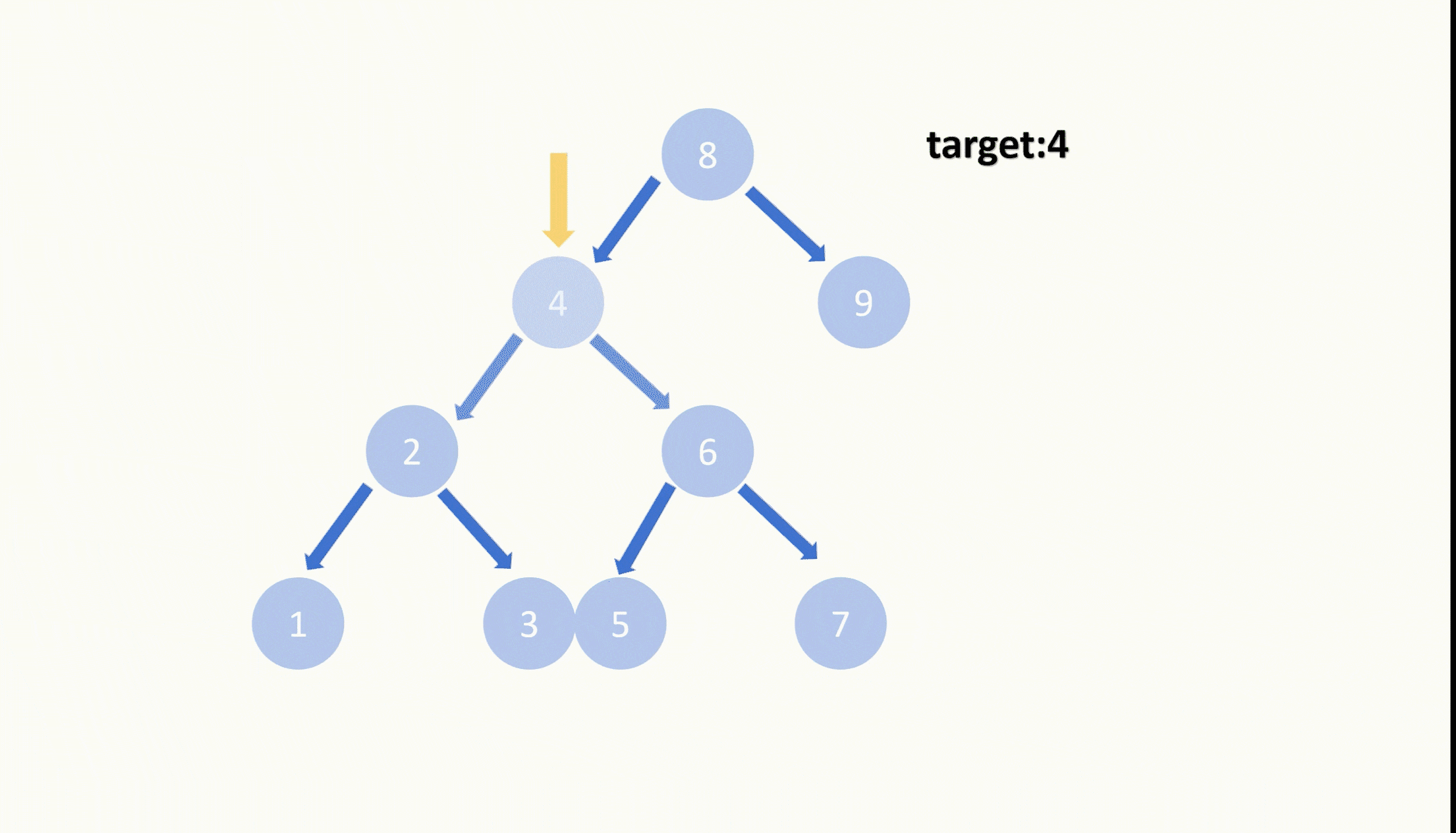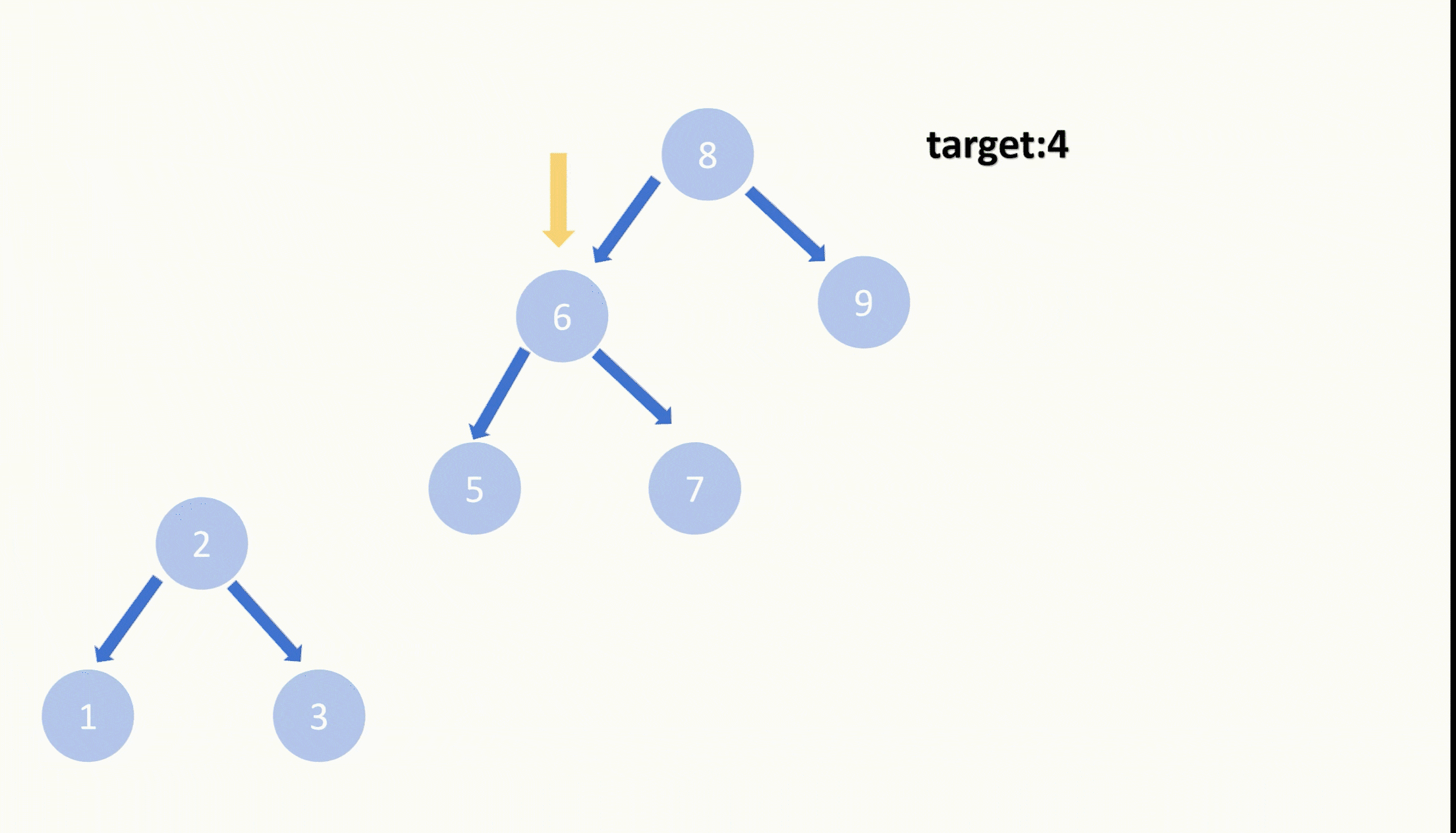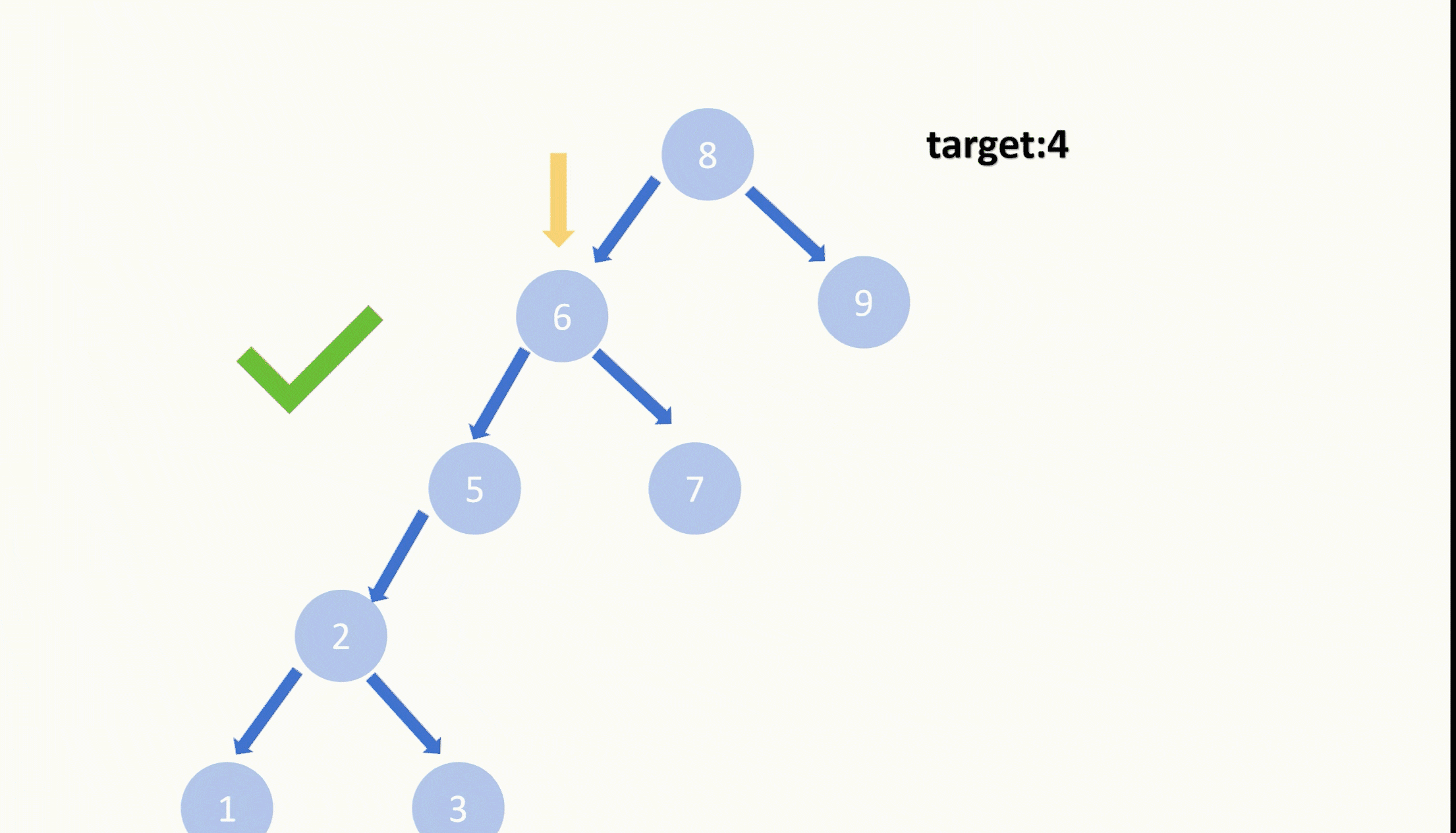
【LeetCode75】第四十二题 删除二叉搜索数中的节点
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 题目给我们一棵二叉搜索树,给我们一个目标值,让我们删除节点值等于目标值的节点,并且删除之后需要保持…...

c++:QT day2 信号和槽
1.多态: 静态多态:函数的重载 动态多态:程序运行 多态的实现:父类的指针或引用,指向或初始化子类的对象,调用子类对父类重写的函数,进而展开子类的功能 2.虚函数:用virtua关键字修饰的函数是虚函…...
16 Linux之JavaEE定制篇-搭建JavaEE环境
16 Linux之JavaEE定制篇-搭建JavaEE环境 文章目录 16 Linux之JavaEE定制篇-搭建JavaEE环境16.1 概述16.2 安装JDK16.3 安装tomcat16.4 安装idea2020*16.5 安装mysql5.7 学习视频来自于B站【小白入门 通俗易懂】2021韩顺平 一周学会Linux。可能会用到的资料有如下所示࿰…...

AI人员打闹监测识别算法
AI人员打闹监测识别算法通过yolopython网络模型框架算法, AI人员打闹监测识别算法能够准确判断出是否有人员进行打闹行为,算法会立即发出预警信号。Yolo算法,其全称是You Only Look Once: Unified, Real-Time Object Detection,其…...

如何使用CRM系统进行精细化管理客户?
客户是企业的生命线,对客户进行精细化管理,是提高企业收益的关键。那么,如何进行客户管理?CRM系统可以实现精细化管理客户,提升客户的价值。下面我们就来详细说一说。 1、获取客户信息 Zoho CRM系统可以通过web表单、…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
