LA@方阵相似@相似矩阵的性质
文章目录
- 相似矩阵
- 引言
- 相似矩阵定义
- 相似变换
- 相似变换矩阵
- 相似矩阵的矩阵多项式和特征值相同
- 推论:与对角阵相似的矩阵性质定理
- 相似矩阵性质
- 相似矩阵的乘方性质
- 相似矩阵和矩阵多项式
- 相似对角阵
- 对角阵多项式的展开
- 小结
相似矩阵
引言
- 对角阵是矩阵中最简单的一类矩阵
- 对角阵相关的乘法运算是很高效的
- 相似方阵是和对角阵相关的概念
相似矩阵定义
- 设 A , B \bold{{A},\bold{B}} A,B是 n n n阶方阵,如果存在 n n n阶可逆方阵 P \bold{P} P,使得 P − 1 A P = B \bold{P^{-1}{AP}={B}} P−1AP=B,则称方阵 A , B \bold{A},\bold{B} A,B相似,记为 A ∼ B \bold{A}\sim{\bold{B}} A∼B
相似变换
- 对 A \bold{A} A进行运算 P − 1 A P \bold{P^{-1}AP} P−1AP称为对 A \bold{A} A进行相似变换
相似变换矩阵
- 矩阵 P \bold{P} P称为相似变换 P − 1 A P \bold{P^{-1}AP} P−1AP的相似变换矩阵
相似矩阵的矩阵多项式和特征值相同
-
若 n n n阶矩阵 A , B \bold{A,B} A,B相似,则 A , B \bold{A,B} A,B的特征多项式相同,从而 A , B \bold{A,B} A,B的特征值相同
-
证明:
- 由 A ∼ B \bold{A\sim{B}} A∼B,有 P \bold{P} P满足 P − 1 A P = B \bold{P^{-1}AP=B} P−1AP=B
- 所以 f B ( λ ) f_{\bold{B}}(\lambda) fB(λ)= ∣ B − λ E ∣ \bold{|B-\lambda{E}|} ∣B−λE∣= ∣ P − 1 A P − λ E ∣ |\bold{P^{-1}AP-\lambda{E}}| ∣P−1AP−λE∣
- 由于 P λ E P − 1 \bold{P\lambda{E}P^{-1}} PλEP−1= λ P E P − 1 \lambda\bold{PEP^{-1}} λPEP−1= λ P P − 1 \lambda\bold{PP^{-1}} λPP−1= λ E \lambda\bold{E} λE,因此,可以将 λ E \bold{\lambda{E}} λE变形为 P ( λ E ) P − 1 \bold{P(\lambda{E})P^{-1}} P(λE)P−1或 P − 1 ( λ E ) P \bold{P^{-1}(\lambda{E})P} P−1(λE)P
- f B ( λ ) = ∣ P − 1 A P − P − 1 ( λ E ) P ∣ f_{\bold{B}}(\lambda)=|\bold{P^{-1}AP-\bold{P^{-1}(\lambda{E})P}}| fB(λ)=∣P−1AP−P−1(λE)P∣= ∣ P − 1 ( A − λ E ) P ∣ |\bold{P^{-1}(A-\lambda{E})P}| ∣P−1(A−λE)P∣= ∣ P − 1 ∣ ∣ A − λ E ∣ ∣ P ∣ \bold{|P^{-1}||A-\lambda{E}||P|} ∣P−1∣∣A−λE∣∣P∣= ∣ P ∣ − 1 ∣ A − λ E ∣ ∣ P ∣ \bold{|P|^{-1}|A-\lambda{E}||P|} ∣P∣−1∣A−λE∣∣P∣= ∣ A − λ E ∣ \bold{|A-\lambda{E}|} ∣A−λE∣
- 显然 f A ( λ ) = f B ( λ ) f_{\bold{A}}(\lambda)=f_{\bold{B}}(\lambda) fA(λ)=fB(λ)
-
但是,特征值相同的方阵未必相似
推论:与对角阵相似的矩阵性质定理
-
与对角阵相似的矩阵的特征值就是对角阵对角元素
-
若 n n n阶矩阵 A ∼ Λ ( λ 1 , ⋯ , λ n ) \bold{A}\sim{\Lambda(\lambda_1,\cdots,\lambda_n)} A∼Λ(λ1,⋯,λn),则 λ 1 , ⋯ , λ n \lambda_1,\cdots,\lambda_n λ1,⋯,λn是 A A A的 n n n个特征值
-
证明:对角阵的特征值是对角元素,由本节定理可知, A \bold{A} A的特征值与 Λ \Lambda Λ相同,所以推论成立
相似矩阵性质
-
A ∼ A \bold{A}\sim{\bold{A}} A∼A
-
A ∼ B ⇒ B ∼ A \bold{A}\sim{\bold{B}}\Rightarrow{\bold{B}\sim{\bold{A}}} A∼B⇒B∼A
- P − 1 A P = B , A = P B P − 1 \bold{P}^{-1}\bold{A}\bold P=\bold{B},\bold{A}=\bold P\bold{B}\bold P^{-1} P−1AP=B,A=PBP−1
-
A ∼ B , B ∼ C ⇒ A ∼ C \bold{A}\sim{\bold{B}},\bold{B}\sim{\bold C}\Rightarrow{\bold{A}\sim{\bold C}} A∼B,B∼C⇒A∼C
- P − 1 A P = B , Q − 1 B Q = C \bold{P^{-1}{A}P=\bold{B},Q^{-1}\bold{B}Q=C} P−1AP=B,Q−1BQ=C
- Q C Q − 1 = B = P − 1 A P \bold{QCQ^{-1}=\bold{B}=P^{-1}\bold{A}P} QCQ−1=B=P−1AP
- P Q C Q − 1 P − 1 = A \bold{PQCQ^{-1}P^{-1}=\bold{A}} PQCQ−1P−1=A
- ( P Q ) − 1 = Q − 1 P − 1 \bold{(PQ)^{-1}=Q^{-1}P^{-1}} (PQ)−1=Q−1P−1
- 因此 C ∼ A \bold{C\sim{{A}}} C∼A
-
单位矩阵只和自身相似
- 设方阵 A \bold{A} A和单位阵 E \bold{E} E相似
- P − 1 A P = E \bold{P^{-1}{A}P=E} P−1AP=E
- A = P E P − 1 = E \bold{A=PEP^{-1}=E} A=PEP−1=E
- 因此和单位阵 E \bold{E} E相似的矩阵是 E \bold{E} E本身
-
∣ A ∣ = ∣ B ∣ |\bold{A}|=|\bold{B}| ∣A∣=∣B∣
- ∣ B ∣ = ∣ P − 1 B P ∣ = ∣ P − 1 ∣ ∣ B ∣ ∣ P ∣ = ∣ P ∣ − 1 ∣ P ∣ ∣ B ∣ = B |\bold{B}|=|P^{-1}\bold{B}P|=|P^{-1}||\bold{B}||P|=|P|^{-1}|P||\bold{B}|=\bold{B} ∣B∣=∣P−1BP∣=∣P−1∣∣B∣∣P∣=∣P∣−1∣P∣∣B∣=B
-
t r ( A ) = t r ( B ) tr(\bold{A})=tr(\bold{B}) tr(A)=tr(B)
- A , B \bold{A},\bold{B} A,B具有相同的特征值
- t r ( A ) = ∑ i = 1 n a i i = ∑ i = 1 n λ i tr(\bold{A})=\sum\limits_{i=1}^{n}a_{ii}=\sum\limits_{i=1}^{n}\lambda_{i} tr(A)=i=1∑naii=i=1∑nλi
- t r ( B ) = ∑ i = 1 n b i i = ∑ i = 1 n λ i tr(\bold{B})=\sum\limits_{i=1}^{n}b_{ii}=\sum\limits_{i=1}^{n}\lambda_{i} tr(B)=i=1∑nbii=i=1∑nλi
- ∴ t r ( A ) = t r ( B ) \therefore tr(\bold{A})=tr(\bold{B}) ∴tr(A)=tr(B)
-
r ( A ) = r ( B ) r(\bold{A})=r(\bold{B}) r(A)=r(B)
- A = P − 1 B P \bold{A}=P^{-1}\bold{B}P^{} A=P−1BP
- P , P − 1 P,P^{-1} P,P−1都是可逆矩阵,它们都可以表示为一系列的初等矩阵的乘积
- 因此, A \bold{A} A相当于有 B \bold{B} B经过初等变换得到的等价矩阵,它们的秩相等(初等变换不改变秩)
- A = P − 1 B P \bold{A}=P^{-1}\bold{B}P^{} A=P−1BP
-
A T ∼ B T \bold{A}^T\sim{\bold{B}^T} AT∼BT
- P − 1 A P = B \bold{P^{-1}{A}P={B}} P−1AP=B
- Q − 1 B Q = A \bold{Q^{-1}{B}Q={A}} Q−1BQ=A
- ( P − 1 A P ) T = B T \bold{(P^{-1}{A}P)^T={B}^T} (P−1AP)T=BT
- P T A T ( P − 1 ) T = B T P^T\bold{A}^T(P^{-1})^T=\bold{B}^T PTAT(P−1)T=BT
- P T A T ( P T ) − 1 = B T P^T\bold{A}^T(P^{T})^{-1}=\bold{B}^T PTAT(PT)−1=BT
- 可见 A T ∼ B T \bold{A}^T\sim{\bold{B}^T} AT∼BT
-
A m ∼ B m \bold{A}^m\sim{\bold{B}^m} Am∼Bm
- B m = ( P − 1 A P ) m = ( P − 1 A P ) ( P − 1 A P ) ⋯ ( P − 1 A P ) \bold{B}^m=(P^{-1}\bold{A}P)^m=(P^{-1}\bold{A}P)(P^{-1}\bold{A}P)\cdots{(P^{-1}\bold{A}P)} Bm=(P−1AP)m=(P−1AP)(P−1AP)⋯(P−1AP)
- = P − 1 A ( P P − 1 ) A ( P ⋯ P − 1 ) A P =P^{-1}\bold{A}(PP^{-1})\bold{A}(P\cdots{P^{-1})\bold{A}P} =P−1A(PP−1)A(P⋯P−1)AP
- = P − 1 A m P =P^{-1}\bold{A}^mP =P−1AmP
- P − 1 A m P = B m P^{-1}\bold{A}^mP=\bold{B}^m P−1AmP=Bm
- B m = ( P − 1 A P ) m = ( P − 1 A P ) ( P − 1 A P ) ⋯ ( P − 1 A P ) \bold{B}^m=(P^{-1}\bold{A}P)^m=(P^{-1}\bold{A}P)(P^{-1}\bold{A}P)\cdots{(P^{-1}\bold{A}P)} Bm=(P−1AP)m=(P−1AP)(P−1AP)⋯(P−1AP)
-
若 A − 1 \bold{A}^{-1} A−1存在,则 B − 1 \bold{B}^{-1} B−1存在, A − 1 ∼ B − 1 , A ∗ ∼ B ∗ \bold{A}^{-1}\sim{\bold{B}^{-1}},\bold{A}^*\sim{\bold{B}^*} A−1∼B−1,A∗∼B∗
-
B \bold{B} B可逆:
- 方法1:
- A ∼ B ⇒ ∣ A ∣ = ∣ B ∣ = k \bold{A}\sim{\bold{B}}\Rightarrow{|\bold{A}|=|\bold{B}|}=k A∼B⇒∣A∣=∣B∣=k
- A − 1 \bold{A}^{-1} A−1存在, ∣ A ∣ ≠ 0 |\bold{A}|\neq{0} ∣A∣=0,则 ∣ B ∣ = ∣ A ∣ ≠ 0 |\bold{B}|=|\bold{A}|\neq{0} ∣B∣=∣A∣=0
- 方法2:
- 由于\bold{A}可逆,则 P − 1 A P = B P^{-1}\bold{A}P=\bold{B} P−1AP=B表明, B \bold{B} B是可逆矩阵的乘积,所以\bold{B}也可逆
-
A − 1 = P B − 1 P − 1 \bold{A}^{-1}=P\bold{B}^{-1}P^{-1} A−1=PB−1P−1,因此 B − 1 ∼ A − 1 \bold{B}^{-1}\sim{\bold{A}^{-1}} B−1∼A−1
- 设 P − 1 A − 1 P = B − 1 P^{-1}\bold{A}^{-1}P=\bold{B}^{-1} P−1A−1P=B−1
- A − 1 = 1 ∣ A ∣ A ∗ = k − 1 A ∗ \bold{A}^{-1}=\frac{1}{|\bold{A}|}\bold{A}^*=k^{-1}\bold{A}^* A−1=∣A∣1A∗=k−1A∗
- B − 1 = 1 ∣ B ∣ B ∗ = k − 1 B ∗ \bold{B}^{-1}=\frac{1}{|\bold{B}|}\bold{B}^{*}=k^{-1}\bold{B}^* B−1=∣B∣1B∗=k−1B∗
- P − 1 k − 1 A ∗ P = k − 1 B ∗ P^{-1}k^{-1}\bold{A}^*P=k^{-1}\bold{B}^* P−1k−1A∗P=k−1B∗
- P − 1 A ∗ P = B ∗ P^{-1}\bold{A}^*P=\bold{B}^* P−1A∗P=B∗
- 设 P − 1 A − 1 P = B − 1 P^{-1}\bold{A}^{-1}P=\bold{B}^{-1} P−1A−1P=B−1
-
相似矩阵的乘方性质
设 A , B \bold{A,B} A,B相似 A = P B k P − 1 \bold{A=PB}^k\bold{P}^{-1} A=PBkP−1<0>
- A k \bold{A}^k Ak= P B k P − 1 \bold{P}\bold{B}^k{\bold{P}^{-1}} PBkP−1
<1>- 推导: A k \bold{A}^k Ak= ( P B P − 1 ) ( P B P − 1 ) ⋯ ( P B P − 1 ) (\bold{P}\bold{B}{\bold{P}^{-1}})(\bold{P}\bold{B}{\bold{P}^{-1}})\cdots(\bold{P}\bold{B}{\bold{P}^{-1}}) (PBP−1)(PBP−1)⋯(PBP−1)
- = P B ( P − 1 P ) B ( P − 1 P ) B ⋯ B ( P − 1 P ) B P − 1 \bold{P}\bold{B}(\bold{P}^{-1}\bold{P})\bold{B}{(\bold{P}^{-1}\bold{P})}\bold{B}\cdots\bold{B}(\bold{P}^{-1}\bold{P})\bold{B}{\bold{P}^{-1}} PB(P−1P)B(P−1P)B⋯B(P−1P)BP−1
- = P B k P − 1 \bold{P}\bold{B}^k{\bold{P}^{-1}} PBkP−1
- 推导: A k \bold{A}^k Ak= ( P B P − 1 ) ( P B P − 1 ) ⋯ ( P B P − 1 ) (\bold{P}\bold{B}{\bold{P}^{-1}})(\bold{P}\bold{B}{\bold{P}^{-1}})\cdots(\bold{P}\bold{B}{\bold{P}^{-1}}) (PBP−1)(PBP−1)⋯(PBP−1)
相似矩阵和矩阵多项式
- 设矩阵多项式 f ( A ) = ∑ i = 0 m a i A i f(\bold{A})=\sum\limits_{i=0}^{m}a_i\bold{A}^i f(A)=i=0∑maiAi
<2>,将<1>代入<2>有: f ( A ) f(\bold{A}) f(A)= ∑ i = 0 m a i A i \sum\limits_{i=0}^{m}a_i\bold{A}^i i=0∑maiAi= ∑ i = 0 m a i ( P B i P − 1 ) ) \sum\limits_{i=0}^{m}a_i(\bold P\bold{B}^i{\bold P^{-1}})) i=0∑mai(PBiP−1))= ∑ i = 0 m P ( a i B i ) P − 1 \sum\limits_{i=0}^{m}\bold P(a_i\bold{B}^i){\bold P^{-1}} i=0∑mP(aiBi)P−1,根据矩阵乘法的分配律, f ( A ) f(\bold{A}) f(A)= P ( ∑ i = 0 m a i B i ) P − 1 \bold{P}(\sum_{i=0}^{m}a_i\bold{B}^{i})\bold{P}^{-1} P(∑i=0maiBi)P−1= P f ( B ) P − 1 \bold Pf(\bold{{B}})\bold P^{-1} Pf(B)P−1
相似对角阵
-
当 A \bold{A} A相似于某个对角阵 Λ \bold{\Lambda} Λ,则:
- A k \bold{A}^k Ak= P Λ k P − 1 \bold{P}\bold{\Lambda}^k{\bold{P}^{-1}} PΛkP−1
- f ( A ) f(\bold{A}) f(A)= P f ( Λ ) P − 1 \bold Pf(\bold{{\Lambda}})\bold P^{-1} Pf(Λ)P−1
-
由此可见,若矩阵 A \bold{A} A能够表示成 A = P Λ P − 1 \bold{A}=\bold P\Lambda{\bold P^{-1}} A=PΛP−1(相似对角化问题),矩阵 A \bold{A} A的多项式问题就能够被转换为对角阵的多项式
对角阵多项式的展开
-
f ( Λ ) = ∑ i = 0 m a i Λ i f(\bold\Lambda)=\sum_{i=0}^{m}a_{i}\bold\Lambda^{i} f(Λ)=∑i=0maiΛi= diag ( f ( λ 1 ) , f ( λ 2 ) , ⋯ , f ( λ n ) ) \text{diag}(f(\lambda_1),f(\lambda_2),\cdots,f(\lambda_n)) diag(f(λ1),f(λ2),⋯,f(λn)),
-
推导:
-
对角阵乘方运算性质:若 Λ = d i a g ( λ 1 , λ 2 , ⋯ , λ n ) \bold\Lambda=\mathrm{diag}(\lambda_1,\lambda_{2},\cdots,\lambda_{n}) Λ=diag(λ1,λ2,⋯,λn)为对角阵,则 Λ k \bold\Lambda^k Λk= d i a g ( λ 1 k , λ 2 k , ⋯ , λ n k ) \mathrm{diag}(\lambda_1^k,\lambda_{2}^k,\cdots,\lambda_{n}^k) diag(λ1k,λ2k,⋯,λnk)
-
f ( Λ ) = a 0 ( 1 1 ⋱ 1 ) + a 1 ( λ 1 λ 2 ⋱ λ n ) + ⋯ + a n ( λ 1 n λ 2 n ⋱ λ n n ) = ( ∑ i = 0 m a i λ 1 i ∑ i = 0 m a i λ 2 i ⋱ ∑ i = 0 m a i λ n i ) = ( f ( λ 1 ) f ( λ 2 ) ⋱ f ( λ n ) ) \begin{aligned} f(\Lambda) =&\small{a_0\begin{pmatrix} {{1}} & {} & {} & {} \cr {} & {{ 1}} & {} & {} \cr {} & {} & \ddots & {} \cr {} & {} & {} & {{1}} \cr \end{pmatrix} +a_1\begin{pmatrix} {{\lambda _1}} & {} & {} & {} \cr {} & {{\lambda _2}} & {} & {} \cr {} & {} & \ddots & {} \cr {} & {} & {} & {{\lambda _n}} \cr \end{pmatrix} +\cdots +a_n\begin{pmatrix} {{\lambda _1^n}} & {} & {} & {} \cr {} & {{\lambda _2^n}} & {} & {} \cr {} & {} & \ddots & {} \cr {} & {} & {} & {{\lambda _n^n}} \cr \end{pmatrix}} \\ =&\begin{pmatrix} \sum_{i=0}^{m}a_{i}\lambda_1^{i} & {} & {} & {} \cr {} & \sum_{i=0}^{m}a_{i}\lambda_2^{i} & {} & {} \cr {} & {} & \ddots & {} \cr {} & {} & {} & \sum_{i=0}^{m}a_{i}\lambda_n^{i} \cr \end{pmatrix} =\begin{pmatrix} {f({\lambda _1}}) & {} & {} & {} \cr {} & f({{\lambda _2}}) & {} & {} \cr {} & {} & \ddots & {} \cr {} & {} & {} & f({{\lambda _n}}) \cr \end{pmatrix} \end{aligned} f(Λ)==a0 11⋱1 +a1 λ1λ2⋱λn +⋯+an λ1nλ2n⋱λnn ∑i=0maiλ1i∑i=0maiλ2i⋱∑i=0maiλni = f(λ1)f(λ2)⋱f(λn)
-
这个展开式告诉我们,对角阵(矩阵)的多项式可以归结为数(标量)的多项式的计算
-
小结
- 上述结论说明,相似阵之间有很多共同点
- 特别是,当 A \bold{A} A有一个与之相似的对角阵时,许多关于 A \bold{A} A的计算就可以被简化,例如矩阵多项式的计算,这个问题归结为方阵相似对角化
相关文章:

LA@方阵相似@相似矩阵的性质
文章目录 相似矩阵引言相似矩阵定义相似变换相似变换矩阵相似矩阵的矩阵多项式和特征值相同推论:与对角阵相似的矩阵性质定理 相似矩阵性质相似矩阵的乘方性质相似矩阵和矩阵多项式相似对角阵 对角阵多项式的展开小结 相似矩阵 引言 对角阵是矩阵中最简单的一类矩阵 对角阵相…...
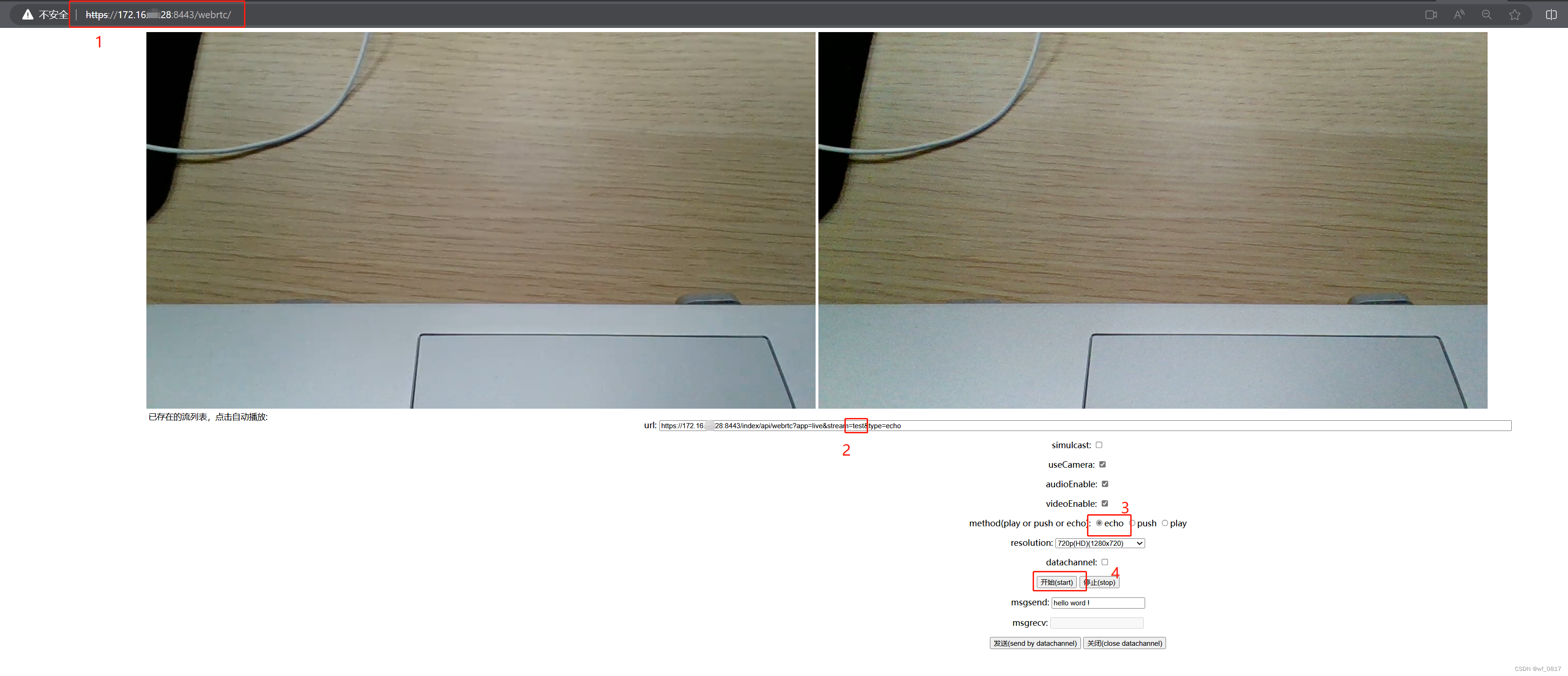
ZLMediaKit 各种推拉流
1 用ffmpeg 推音视频流 ./ffmpeg -f dshow -i video"HP Wide Vision HD Camera" -f dshow -i audio"麦克风阵列 (Realtek High Definition Audio)" -rtbufsize 100M -max_delay 100 -pix_fmt yuv420p -tune zerolatency -c:v libx264 -crf 18 -s 1280x720…...
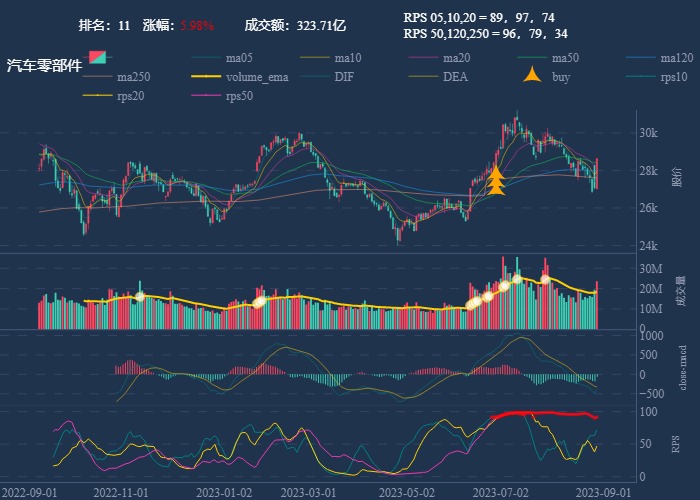
行业追踪,2023-08-29
自动复盘 2023-08-29 凡所有相,皆是虚妄。若见诸相非相,即见如来。 k 线图是最好的老师,每天持续发布板块的rps排名,追踪板块,板块来开仓,板块去清仓,丢弃自以为是的想法,板块去留让…...

【简单】228. 汇总区间
原题链接:https://leetcode.cn/problems/summary-ranges/description/ 228. 汇总区间 给定一个 无重复元素 的 有序 整数数组 nums 。 返回 恰好覆盖数组中所有数字 的 最小有序 区间范围列表 。也就是说,nums 的每个元素都恰好被某个区间范围所覆盖&…...
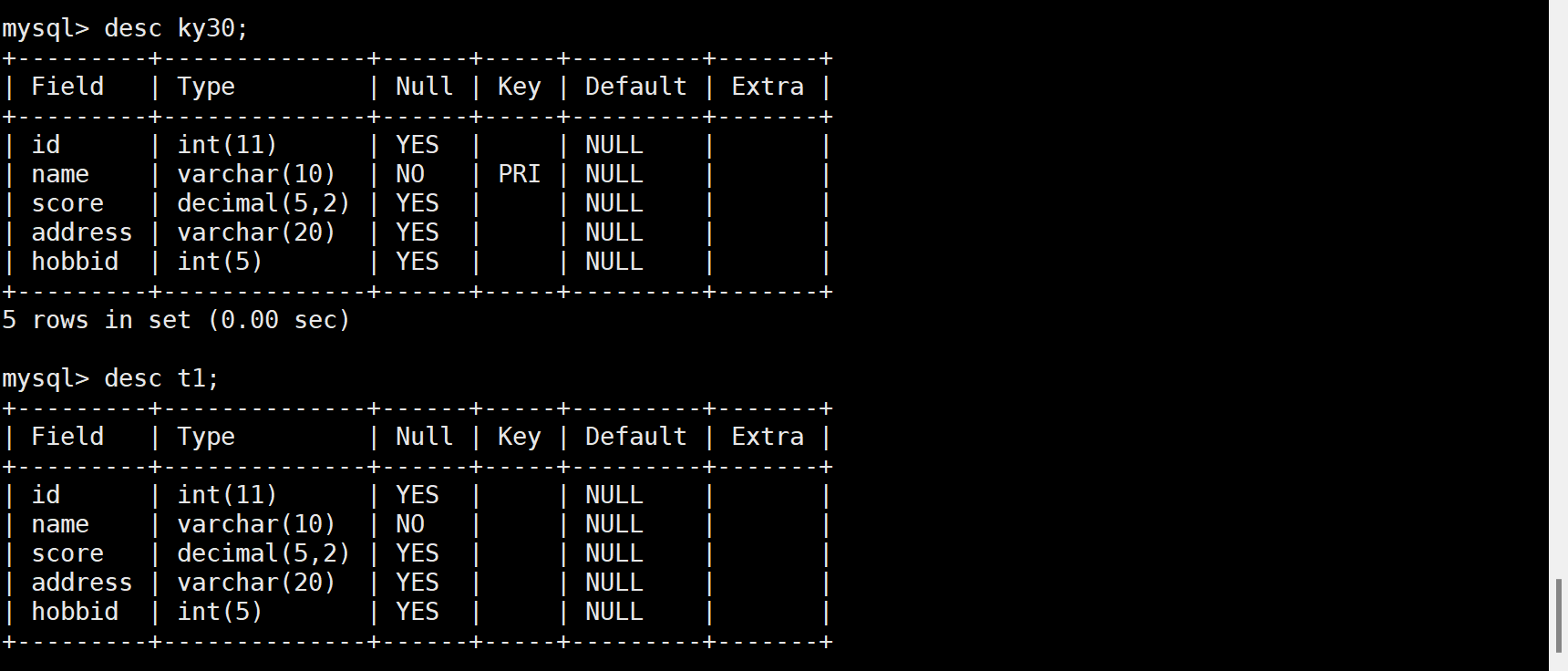
Mysql高级语句
高级语句 1.按关键字排序 SELECT column1, column2, ... FROM table_name ORDER BY column1, column2, ... ASC|DESC ASC 是按照升序进行排序的,是默认的排序方式,即 ASC 可以省略。 SELECT 语句中如果没有指定具体的排序方式,则默认按 ASC…...

Python中 re.compile 函数的使用
前言 嗨喽,大家好呀~这里是爱看美女的茜茜呐 以下介绍在python的re模块中怎样应用正则表达式 👇 👇 👇 更多精彩机密、教程,尽在下方,赶紧点击了解吧~ python源码、视频教程、插件安装教程、资料我都准备…...
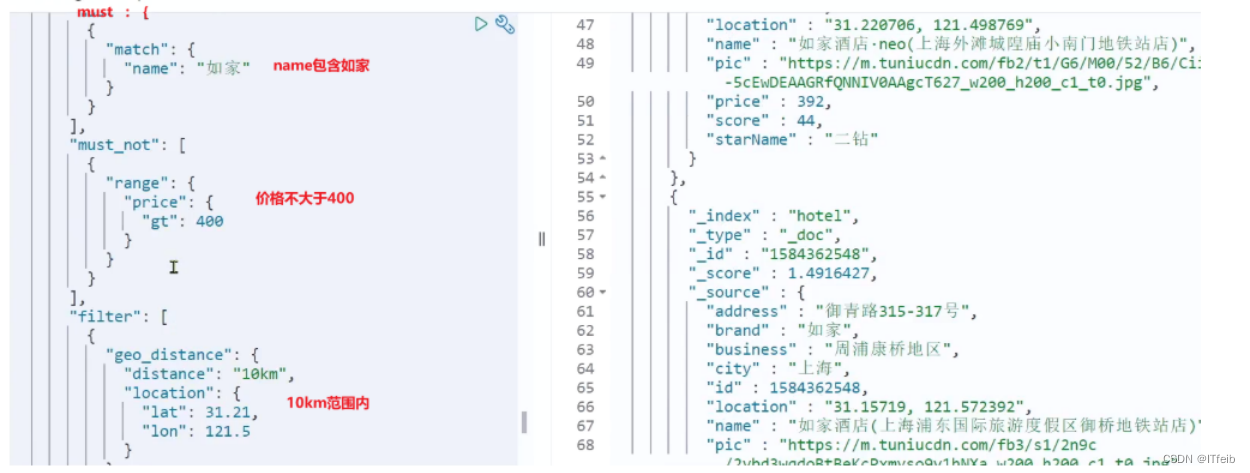
【分布式搜索引擎es】
文章目录 数据搜索DSL实现查询文档搜索结果处理 RestClient实现 elasticsearch最擅长的是 搜索和 数据分析。 数据搜索 DSL实现 查询文档 常见的查询类型包括: 查询所有:查询出所有数据,一般测试用。例如:match_all全文检索…...

单片机的ADC
如何理解ADC。ADC就是将模拟量转换成数字量的过程,就是转换为计算机所能存储的0和1序列,比如将模拟量转换为一个字节,所以这个字节的大小要能反应模拟量的大小,比如一个0-5V的电压测量量(外部输入电压最小0V,最大为5V&…...
如何把pdf文件合并?分享最新pdf合并方法
在所有文档格式中,pdf应该是最常用的,像产品介绍、商务合同、法律文书等等,这些都是pdf格式的。有时候出于工作需要,我们要把两份或者多份pdf文件合并在一起,那么问题来了,如何把pdf文件合并呢?小编最近发…...
)
笙默考试管理系统-MyExamTest----codemirror(11)
笙默考试管理系统-MyExamTest----codemirror(11) 目录 笙默考试管理系统-MyExamTest----codemirror(11) 一、 笙默考试管理系统-MyExamTest----codemirror 二、 笙默考试管理系统-MyExamTest----codemirror 三、 笙默考试管…...
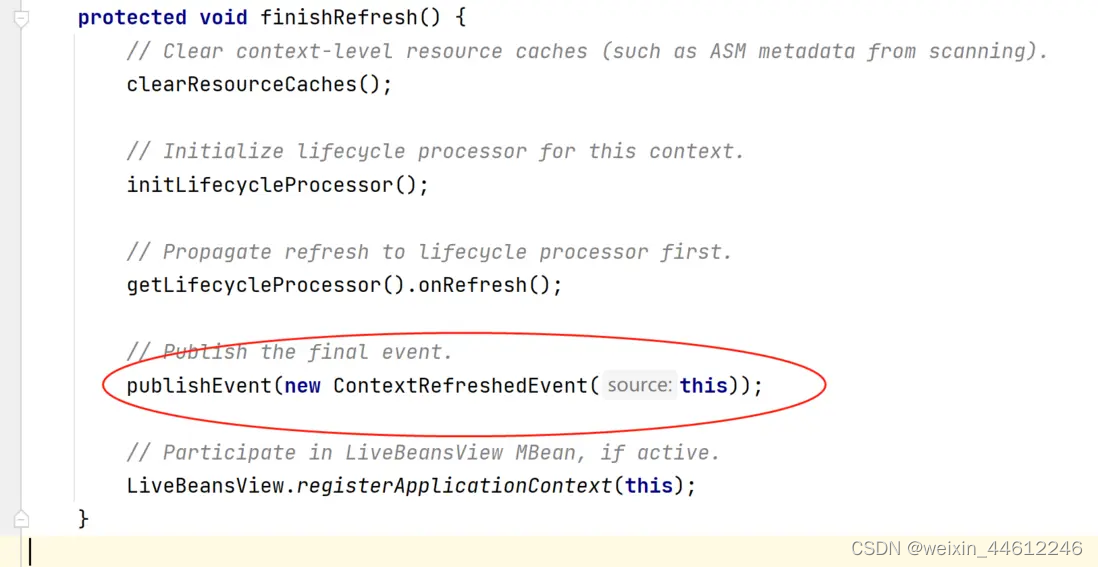
Spring MVC 五 - Spring MVC的配置和DispatcherServlet初始化过程
今天的内容是SpringMVC的初始化过程,其实也就是DispatcherServilet的初始化过程。 Special Bean Types DispatcherServlet委托如下一些特殊的bean来处理请求、并渲染正确的返回。这些特殊的bean是Spring MVC框架管理的bean、按照Spring框架的约定处理相关请求&…...
Ramp 有点意思的题目
粗一看都不知道这个要干什么,这 B 装得不错。 IyEvdXNyL2Jpbi9lbnYgcHl0aG9uMwoKJycnCktlZXAgdXMgb3V0IG9mIGdvb2dsZSBzZWFyY2ggcmVzdWx0cy4uCgokIG9kIC1kIC9kZXYvdXJhbmRvbSB8IGhlYWQKMDAwMDAwMCAgICAgNjAyMTUgICAyODc3OCAgIDI5MjI3ICAgMjg1NDggICA2MjY4NiAgIDQ1MT…...
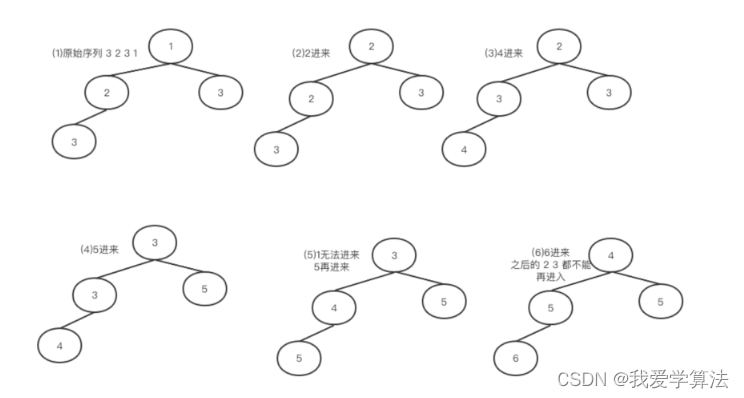
算法通关村14关 | 堆在数组中找第k大的元素应用
1. 在数组中找第k大元素 题目 LeetCode215:给定整数数组nums和整数k,请返回数组中第k个最大的元素, 思路 解题思路用三个,选择法,堆查找和快速排序。 我们选择用大堆小堆解决问题,“找最大用小堆ÿ…...
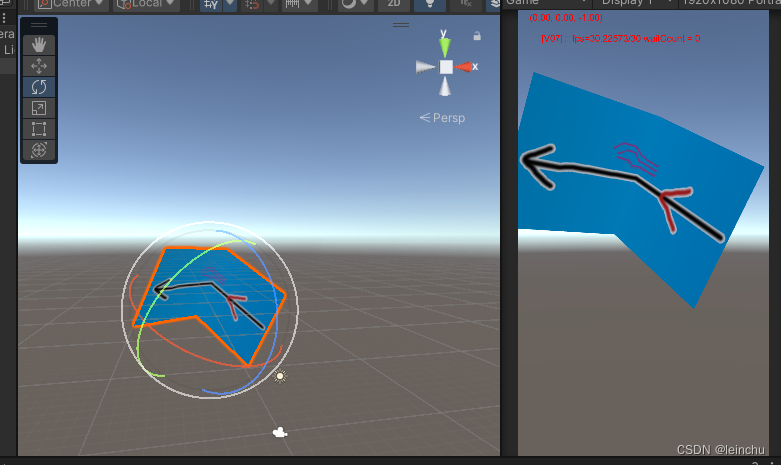
Unity 顶点vertices,uv,与图片贴图,与mesh
mesh就是组成3d物体的三角形们。 mesh由顶点组成的三角形组成,三角形的大小 并不 需要一样,由顶点之间的位置决定。 mesh可以是一个或者多个面。 贴图的原点在左下角,uv是贴图的坐标,数量和顶点数一样(不是100%确定…...

Shell编程之函数
目录 基本概念 自定义函数 系统函数 1.read 2.basename 3.dirname 基本概念 将一段代码组合封装在一起实现某个特定的功能或返回某个特定的值,然后给这段代码取个名字,也就是函数名,在需要实现某个特定功能的时候直接调用函数名即可。 函…...

10.物联网LWIP之TCP状态转变
一。TCP状态机 1.青粗线:理想TCP状态转变(服务器视角下) 2.虚线:被动TCP状态转变(服务器视角下) 3.细实线:不经常出现的TCP状态转变(类似于边界处理) 1.青粗线解释--》服…...

Img标签的src地址自动拼接本地域名(localhost:8080)导致图片不显示问题
摘要:做Vueelement ui项目的时候,发现使用element ui的upload上传图片时,不显示的问题。我项目的图片是上传到七牛云,长传成功后返回存储在七牛云中的地址。后面发现是因为返回的地址是外部地址,需要完整的URL…...

数据结构入门 — 栈
本文属于数据结构专栏文章,适合数据结构入门者学习,涵盖数据结构基础的知识和内容体系,文章在介绍数据结构时会配合上动图演示,方便初学者在学习数据结构时理解和学习,了解数据结构系列专栏点击下方链接。 博客主页&am…...
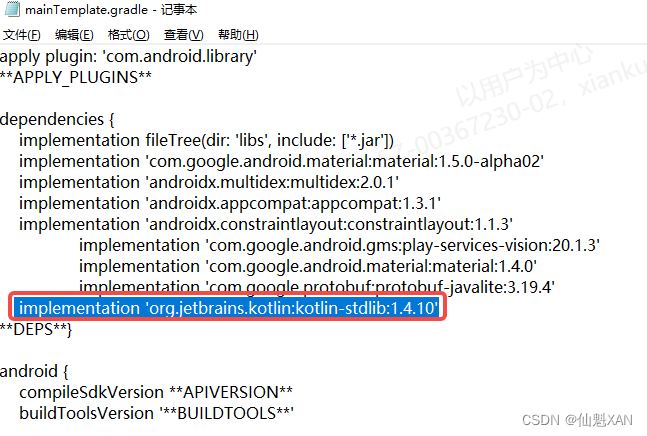
Unity Android 之 在Unity 中引入 OkHttp的操作注意(OKHttp4.xx- kotlin 的包)简单记录
Unity Android 之 在Unity 中引入 OkHttp的操作注意(OKHttp4.xx- kotlin 的包)简单记录 目录 Unity Android 之 在Unity 中引入 OkHttp的操作注意(OKHttp4.xx- kotlin 的包)简单记录 一、简单介绍 二、OKHttp 4.xx 的 SDK 封装 aar 给 Unity 的使用注意 三、附录 OKHttp 的…...

内嵌功能强大、低功耗STM32WB55CEU7、STM32WB55CGU7 射频微控制器 - MCU, 48-UFQFN
一、概述: STM32WB55xx多协议无线和超低功耗器件内嵌功能强大的超低功耗无线电模块(符合蓝牙 低功耗SIG规范5.0和IEEE 802.15.4-2011标准)。该器件内含专用的Arm Cortex -M0,用于执行所有的底层实时操作。这些器件基于高性能Arm …...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
