Matlab(数值微积分)
目录
1.多项式微分与积分
1.1 微分
1.2 多项式微分
1.3 如何正确的使用Matlab?
1.3.1 Matlab表达多项式
1.3.2 polyval() 多项式求值
1.3.3 polyder()多项式微分
1.4 多项式积分
1.4.1 如何正确表达
1.4.2 polyint() 多项式积分
2.数值的微分与积分
2.1 数值微分
2.2 diff() 计算差值
2.3 误差的准确性
2.4 二阶、三阶导数
2.5 数值积分
2.5.1中点规则
2.5.2 梯形规则(trapz)
2.5.3 辛普森积分法
2.5.4 三种积分方式比较
3.函数句柄
3.1 创建函数句柄
3.1.1 有参数的句柄函数
3.1.2 无参数的句柄函数
3.1.3 无参且无括号
3.2 匿名函数
3.3 错误示范
3.4 integral() 数值积分
3.4.1 一级积分
3.4.2 integral2() 二级积分
3.4.3 integral3() 三级积分
1.多项式微分与积分
1.1 微分
- 函数f(x)导数写为:F'(x)或者
- 函数f(x)关于x的变化率
f (x0) 表示点x0处曲线相切的直线的系数。

1.2 多项式微分
对于一个多项式: 来说,其微分多项式为:
1.3 如何正确的使用Matlab?
1.3.1 Matlab表达多项式
在上式中,我们用Matlab应该怎么进行表示(多项式在Matlab中被表示为行向量)
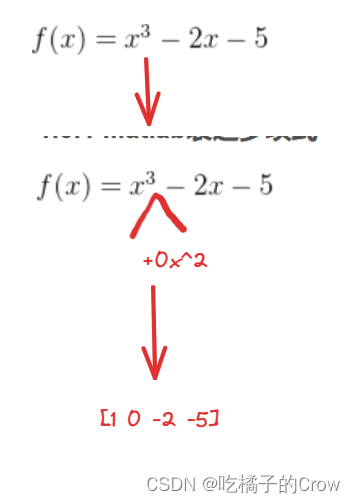
>> p=[1 0 -2 -5]p =1 0 -2 -51.3.2 polyval() 多项式求值
语法:y=polyval(p,x)
y= polyval(p,x) 计算多项式 p 在 x 的每个点处的值。参数 p 是长度为 n+1 的向量,其元素是 n 次多项式的系数(降幂排序):
示例1:
计算多项式 p(x)=3x^2+2x+1在点 x=5、7 、9 处的值。
>> p = [3 2 1];
x = [5 7 9];
y = polyval(p,x)y =86 162 262
示例2:
对该多项式进行画图求值
>> a = [9,-5,3,7]; x = -2:0.01:5;
f = polyval(a,x);
plot(x,f,'LineWidth', 2);%设置线条粗度
xlabel('x轴'); ylabel('f(x)');%设置xy轴名称
set(gca, 'FontSize', 14)%设置字体大小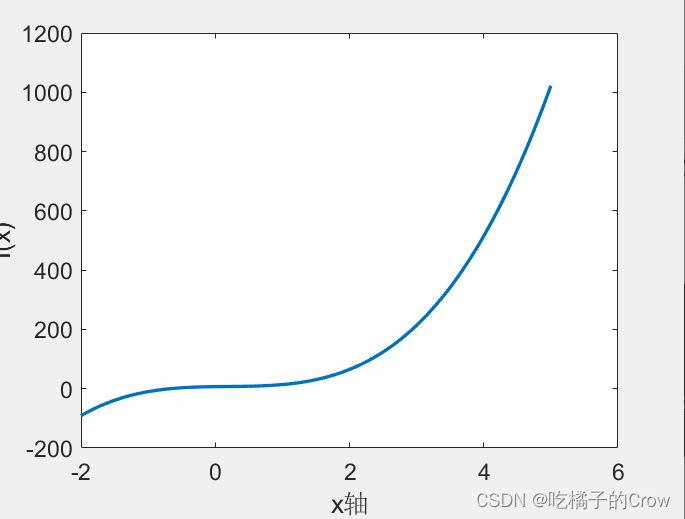
1.3.3 polyder()多项式微分
语法一:k=polyder(p)
k=polyder(p)返回的p中的系数表示的多项式的导数
示例:
创建一个向量来表示多项式 p(x)=3x^5−2x^3+x+5。
p = [3 0 -2 0 1 5]; 使用polyder对多项式进行求导,结果为:
q = polyder(p)
q = 1×515 0 -6 0 1 语法二:k= polyder(a,b) 返回多项式 a 和 b 的乘积的导数
示例:
创建两个向量来表示多项式 a(x)=x^4−2x^3+11 和 b(x)=x^2−10x+15。
a = [1 -2 0 0 11];
b = [1 -10 15];q = polyder(a,b)
q = 1×66 -60 140 -90 22 -110最后的结果为:
语法三:[q,d] = polyder(a,b) 返回多项式 a 和 b 的商的导数
示例:
创建两个向量来表示商中的多项式
p = [1 0 -3 0 -1];
v = [1 4];[q,d] = polyder(p,v)
q = 1×53 16 -3 -24 1d = 1×31 8 16结果为:
1.4 多项式积分
对于一个多项式:
积分多项式为:
1.4.1 如何正确表达
1.4.2 polyint() 多项式积分
语法:q=polyint(p,k) 如果只有的一个参数p,默认k是0,使用积分常量k返回p中的系数所表示的多项积分
示例:
对两个多项式的乘积求积分
- 创建向量来表示多项式
p = [1 0 -1 0 0 1];
v = [1 0 1];- 多项式相乘,并使用积分常量k=3对所生成的表达式求积分
k = 3;
q = polyint(conv(p,v),k)
q = 1×90.1250 0 0 0 -0.2500 0.3333 0 1.0000 3.0000- 通过在积分范围上计算q来求解I的值
a = 0;
b = 2;
I = diff(polyval(q,[a b]))
I = 32.66672.数值的微分与积分
2.1 数值微分
- 最简单的方法:有限差分近似法
- 计算x附近的割线
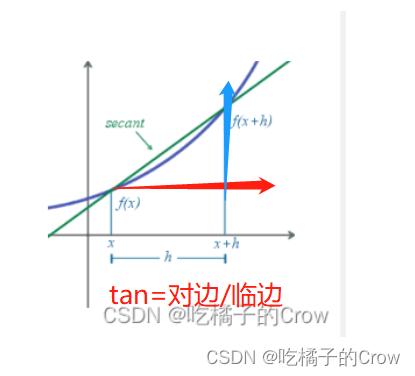
2.2 diff() 计算差值
diff() 计算向量中相邻元素之间的差值
x = [1 2 5 2 1];
diff(x)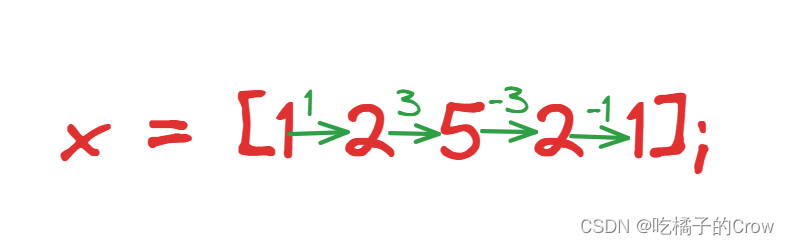
>> x = [1 2 5 2 1];
diff(x)ans =1 3 -3 -1示例:
求出两点之间的斜率
>> x = [1 2]; y = [5 7];
slope = diff(y)./diff(x) %y的变化量/x的变化量slope =22.3 误差的准确性
当
h=0.1、0.01、0.001s时误差有什么变化?
当h=0.1时:
>> x0 = pi/2; h = 0.1;
x = [x0 x0+h];
y = [sin(x0) sin(x0+h)];
m = diff(y)./diff(x)m =-0.0500当h=0.01时:
>> x0 = pi/2; h = 0.01;
x = [x0 x0+h];
y = [sin(x0) sin(x0+h)];
m = diff(y)./diff(x)m =-0.0050当h=0.001时:
>>
x0 = pi/2; h = 0.001;
x = [x0 x0+h];
y = [sin(x0) sin(x0+h)];
m = diff(y)./diff(x)m =-5.0000e-04由分析得:所以当h->0时,误差越小
g = colormap(lines); hold on;
for i=1:4
x = 0:power(10, -i):pi;
y = sin(x); m = diff(y)./diff(x);
plot(x(1:end-1), m, 'Color', g(i,:));%每次微分,系数的个数少1
end
hold off;
set(gca, 'XLim', [0, pi/2]); set(gca, 'YLim', [0, 1.2]);
set(gca, 'FontSize', 18); set(gca, 'FontName', 'symbol');
set(gca, 'XTick', 0:pi/4:pi/2);
set(gca, 'XTickLabel', {'0', 'p/4', 'p/2'});
h = legend('h=0.1','h=0.01','h=0.001','h=0.0001');
set(h,'FontName', 'Times New Roman'); box on;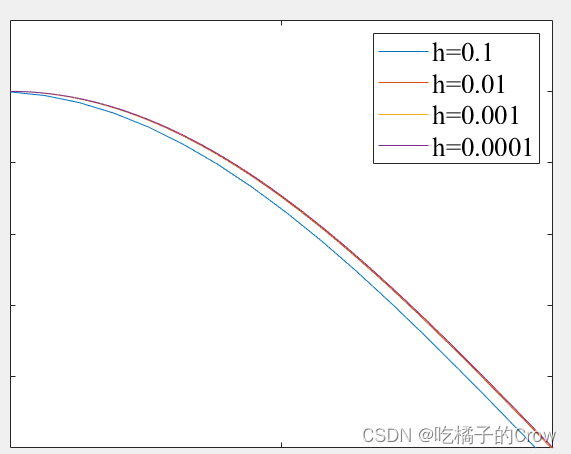
2.4 二阶、三阶导数
>> x = -2:0.005:2; y = x.^3;
m = diff(y)./diff(x);
m2 = diff(m)./diff(x(1:end-1));
plot(x,y,x(1:end-1),m,x(1:end-2),m2);%每次导数系数减1
xlabel('x', 'FontSize', 18);
ylabel('y', 'FontSize', 18);
legend('f(x) =x^3','f''(x)','f''''(x)');
set(gca, 'FontSize', 18);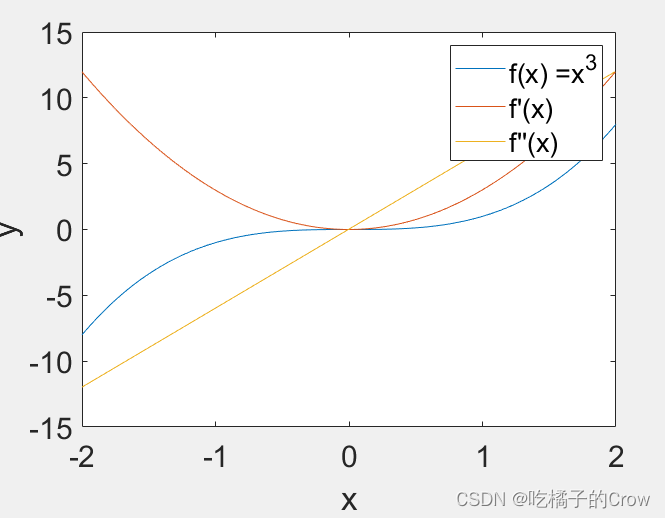
2.5 数值积分
- 求积法——用有限集点逼近积分
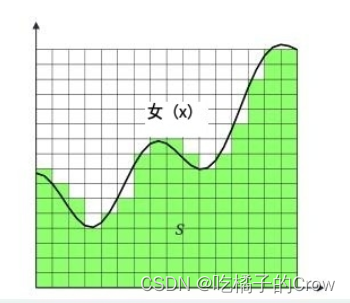
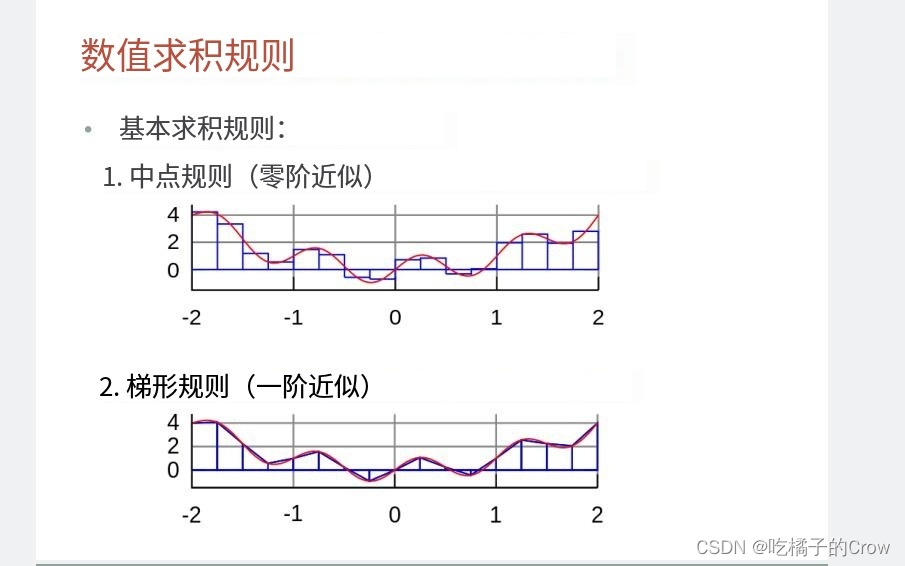
2.5.1中点规则
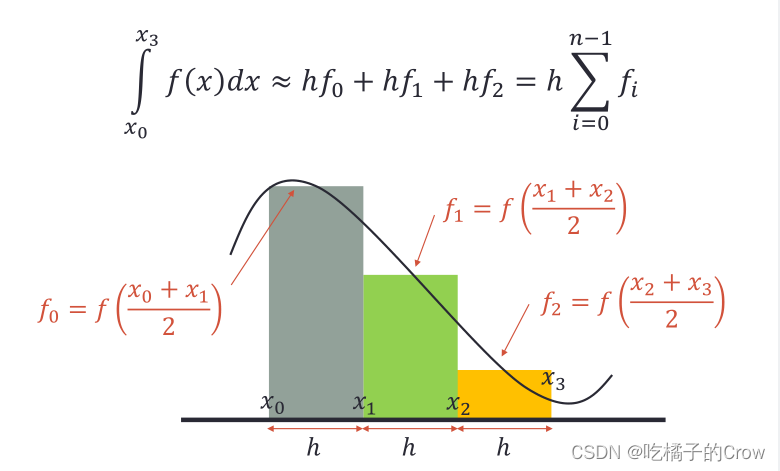
示例:
我们通过积分可以求得:
但是我们通过中点积分可得:
>> h = 0.05; x = 0:h:2;
midpoint = (x(1:end-1)+x(2:end))./2;
y = 4*midpoint.^3;
s = sum(h*y)s =15.9950解释:
midpoint = (x(1:end-1)+x(2:end))./2;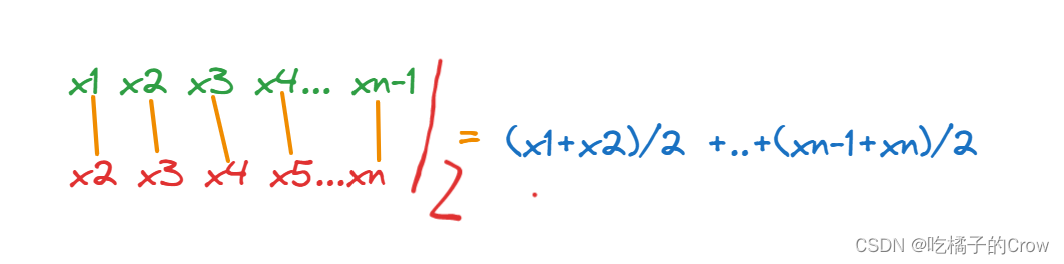
2.5.2 梯形规则(trapz)
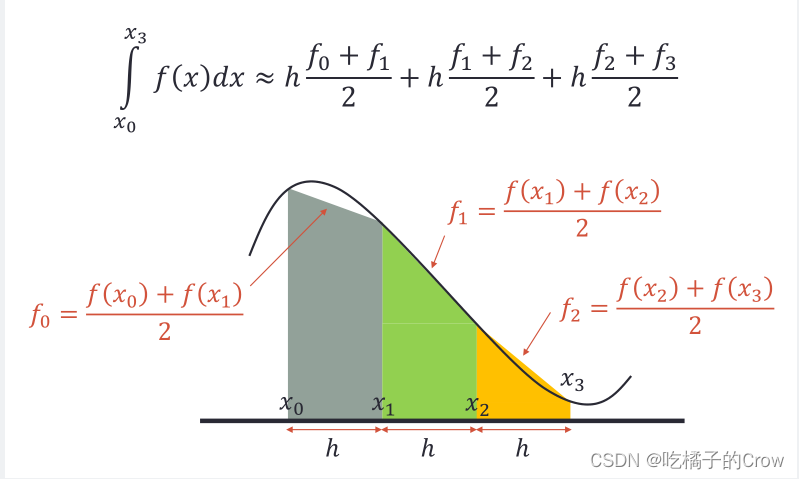
>> h = 0.05; x = 0:h:2; y = 4*x.^3;
s = h*trapz(y)s =16.0100我们也可以自定义该函数:
h = 0.05; x = 0:h:2; y = 4*x.^3;
trapezoid = (y(1:end-1)+y(2:end))/2;
s = h*sum(trapezoid)s =16.01002.5.3 辛普森积分法
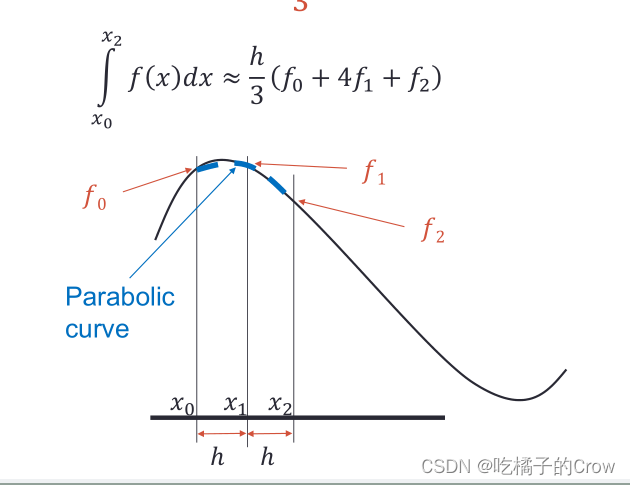
>> h = 0.05; x = 0:h:2; y = 4*x.^3;
s = h/3*(y(1)+2*sum(y(3:2:end-2))+...
4*sum(y(2:2:end))+y(end))s =162.5.4 三种积分方式比较
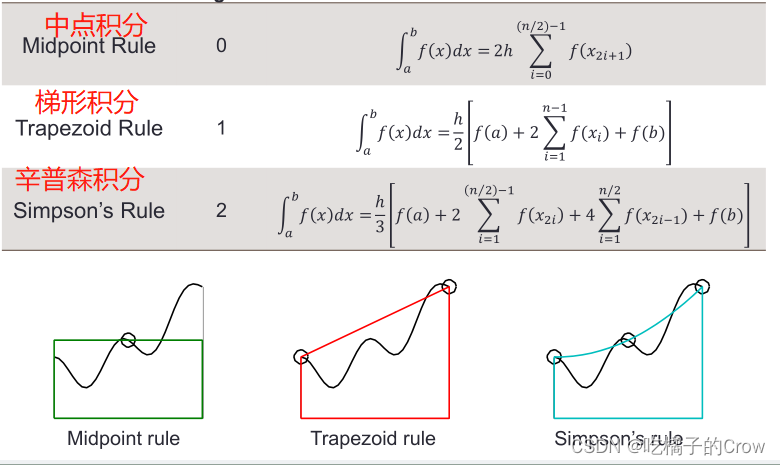
由分析易得: 辛普森积分法误差最小
3.函数句柄
函数句柄是一种存储指向函数的关联关系的Matlab数据类型,间接调用函数使您在调用函数时无需考虑调用位置,函数句柄的典型用法包括:
- 将一个函数传递到另一个函数(通常称为复合函数)
- 指定回调函数
- 构造以内联方式定义而非存储在程序文件(匿名函数)中的函数句柄
- 从主函数外调用局部函数
查看h是否是函数句柄
isa(h,'function_handle')3.1 创建函数句柄
通过在函数名称前添加一个 @ 符号来为函数创建句柄。
f = @myfunction;3.1.1 有参数的句柄函数
使用句柄调用函数的方式与直接调用函数一样,例如:
function y = computeSquare(x)
y = x.^2;
end创建句柄并调用该函数以计算 4 的平方。
f = @computeSquare;
a = 4;
b = f(a)
b =163.1.2 无参数的句柄函数
如果该函数不需要任何输入,则您可以使用空括号调用该函数,例如:
h = @ones;
a = h()
a =1
3.1.3 无参且无括号
如果不使用括号,则该赋值会创建另一个函数句柄。
a = h
a = @ones3.2 匿名函数
您可以创建指向匿名函数的句柄。匿名函数是基于单行表达式的 MATLAB 函数,不需要程序文件。构造指向匿名函数的句柄,方法是定义 anonymous_function 函数主体,以及指向匿名函数 arglist 的以逗号分隔的输入参数列表。语法为:
h = @(arglist)anonymous_function例如,创建一个指向用于计算平方数的匿名函数的句柄 sqr,并使用其句柄调用该匿名函数。
sqr = @(n) n.^2;
x = sqr(3)
x =93.3 错误示范
function [y] = xy_plot(input,x)
% xy_plot receives the handle of a function
% and plots that function of x
y = input(x); plot(x,y,'r--');
xlabel('x'); ylabel('function(x)');
end
>> xy_plot(sin,0:0.01:2*pi)
错误使用 sin
输入参数的数目不足。调用参数的时候,如果该参数也是一个函数,这个时候直接将函数当成参数输入进去是不妥的,会直接报错,这个时候我们就需要句柄
>>
xy_plot(@sin,0:0.01:2*pi)ans =列 1 至 110 0.0100 0.0200 0.0300 0.0400 0.0500 0.0600 0.0699 0.0799 0.0899 0.0998列 12 至 220.1098 0.1197 0.1296 0.1395 0.1494 0.1593 0.1692 0.1790 0.1889 0.1987 0.2085列 23 至 330.2182 0.2280 0.2377 0.2474 0.2571 0.2667 0.2764 0.2860 0.2955 0.3051 0.3146
...3.4 integral() 数值积分
3.4.1 一级积分
我们通过句柄该怎么去解决呢?
>> y = @(x) 1./(x.^3-2*x-5);
integral(y,0,2)ans =-0.46053.4.2 integral2() 二级积分
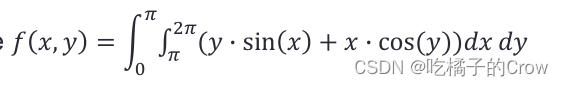
>> f = @(x,y) y.*sin(x)+x.*cos(y);
integral2(f,pi,2*pi,0,pi)ans =-9.86963.4.3 integral3() 三级积分
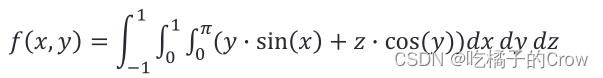
>> f = @(x,y,z) y.*sin(x)+z.*cos(y);
integral3(f,0,pi,0,1,-1,1)ans =2.0000相关文章:
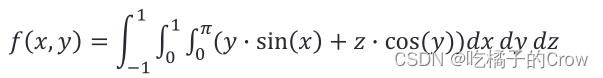
Matlab(数值微积分)
目录 1.多项式微分与积分 1.1 微分 1.2 多项式微分 1.3 如何正确的使用Matlab? 1.3.1 Matlab表达多项式 1.3.2 polyval() 多项式求值 1.3.3 polyder()多项式微分 1.4 多项式积分 1.4.1 如何正确表达 1.4.2 polyint() 多项式积分 2.数值的微分与积分 2.1 数值微分 2…...
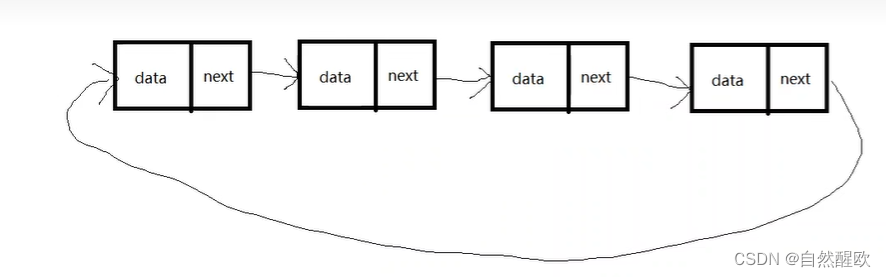
【数据结构回顾】
数据结构回顾 一、单链表二、单循环链表 一、单链表 #include <stdio.h> #include <stdlib.h>typedef struct Node {int data;Node *next; }Node;Node* initList() {Node *list (Node*)malloc(sizeof(Node));list->data 0;list->next NULL;return list; }…...
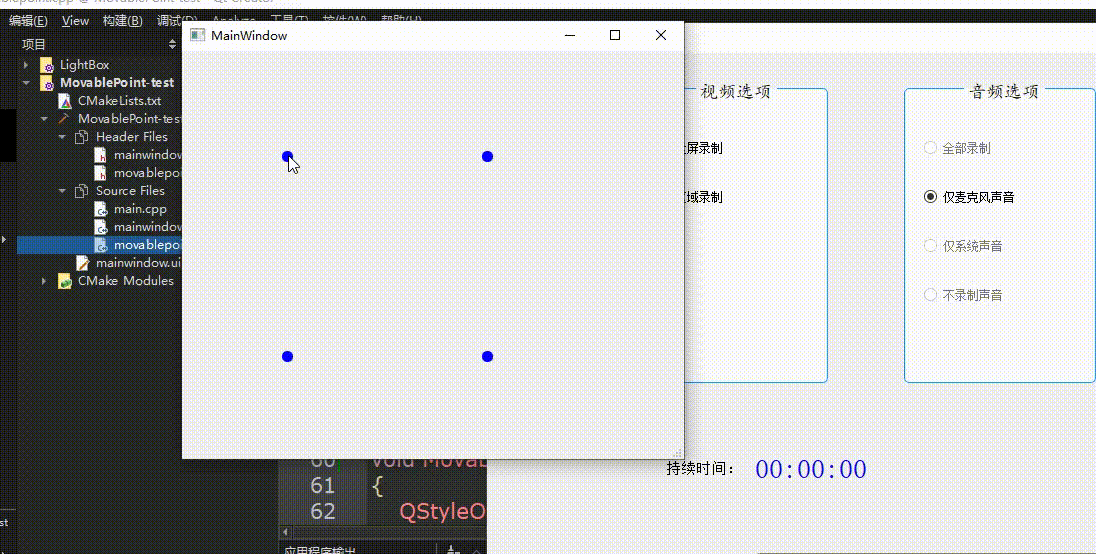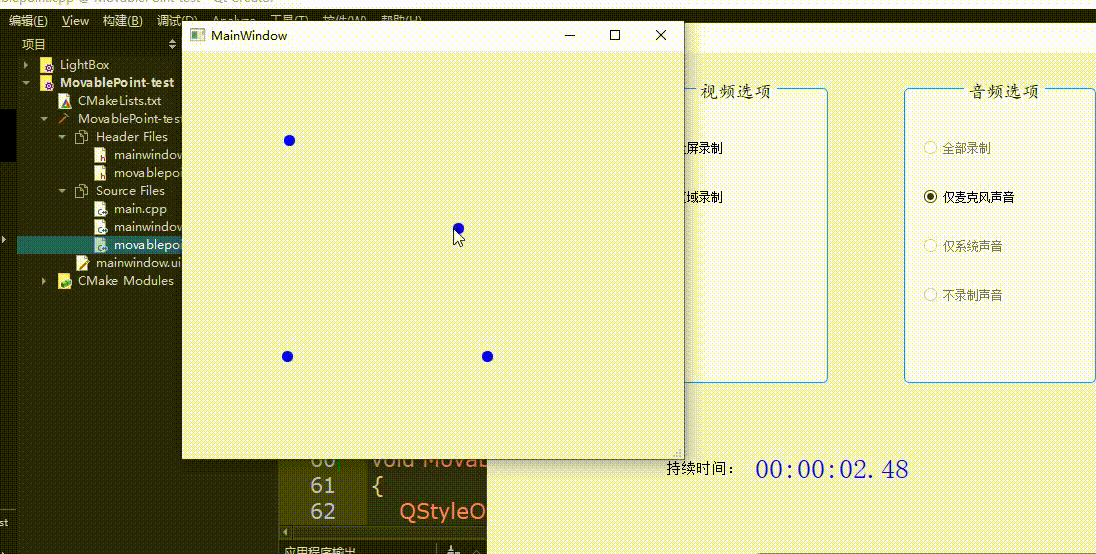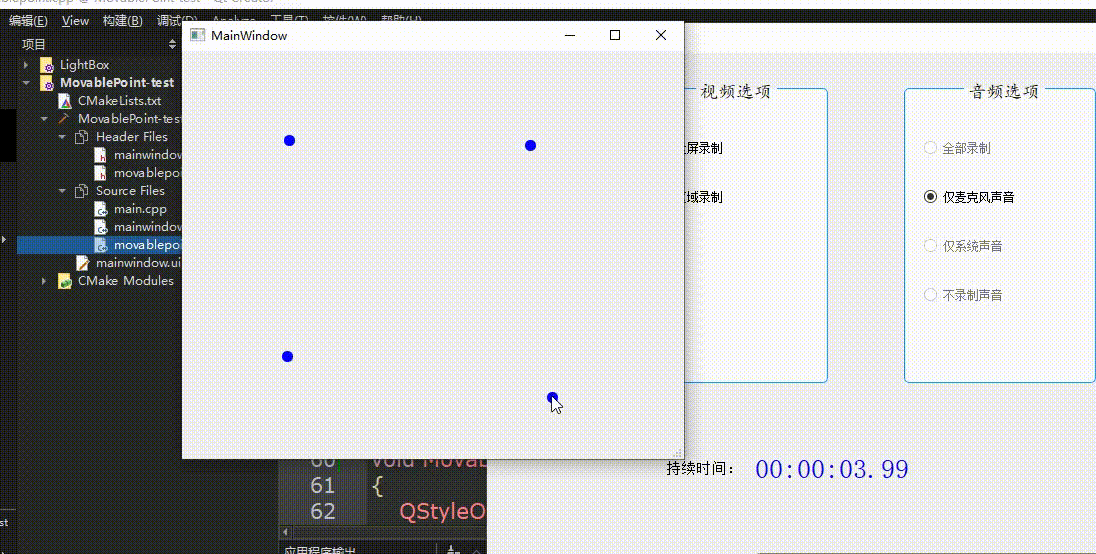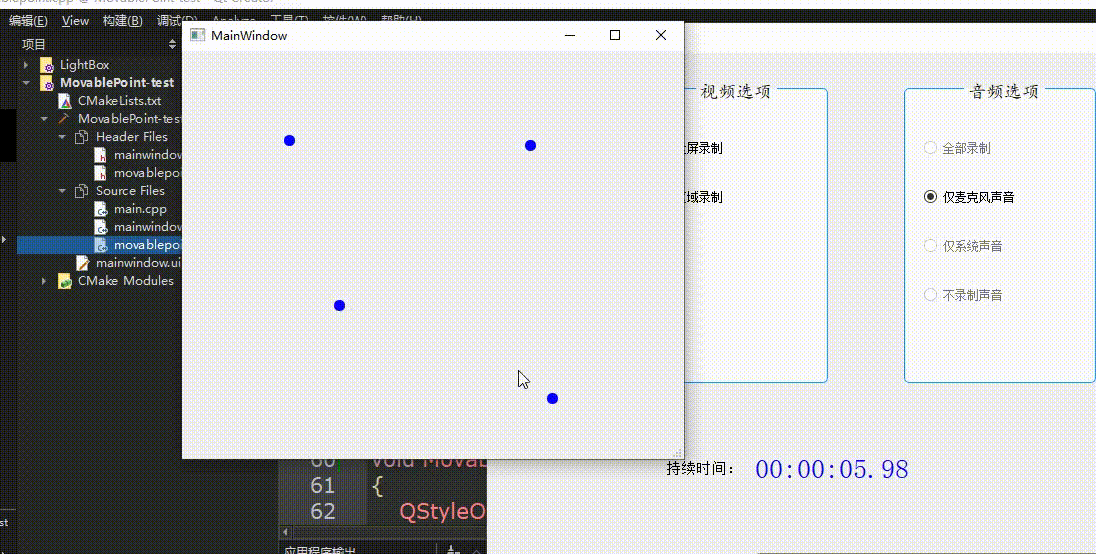
QT创建可移动点类
效果如图所示: 创建新类MovablePoint,继承自QWidget. MovablePoint头文件: #ifndef MOVABLEPOINT_H #define MOVABLEPOINT_H#include <QWidget> #include <QPainter> #include <QPaintEvent> #include <QStyleOption> #includ…...
Flutter启动页
效果图 import dart:async; import package:flutter/cupertino.dart; import package:flutter/material.dart; import jumpPage.dart;class TransitPage extends StatefulWidget {const TransitPage({super.key});overrideState<TransitPage> createState() > _Trans…...
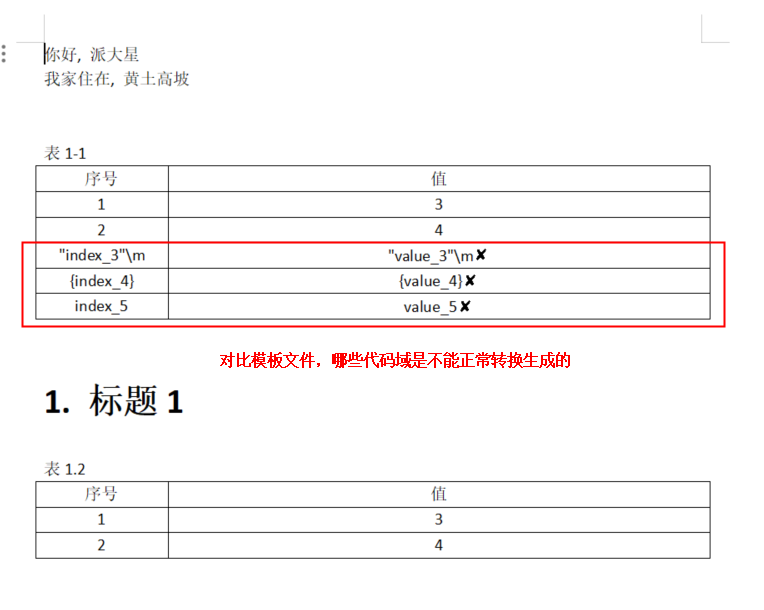
读word模板批量生成制式文件
文章目录 1、Maven依赖2、.docx或.doc格式的word模板准备3、读word模板,批量替换代码域,生成文件,demo4、结果展示 1、Maven依赖 <dependency><groupId>fr.opensagres.xdocreport</groupId><artifactId>fr.opensagre…...
Node.js crypto模块 加密算法
背景 微信小程序调用飞蛾热敏纸打印机,需要进行参数sig签名校验,使用的是sha1进行加密 // 通过crypto.createHash()函数,创建一个hash实例,但是需要调用md5,sha1,sha256,sha512算法来实现实例的…...

Win11 避坑安装WSL2 Ubuntu22.04
开始之前以管理员身份打开 PowerShell 启用适用于 Linux 的 Windows 子系统 需要先启用“适用于 Linux 的 Windows 子系统”可选功能,然后才能在 Windows 上安装 Linux 分发。 PowerShell然后输入以下命令: dism.exe /online /enable-feature /featur…...

ESP8266+继电器+MQTT+VUE 实现远程开关灯
超详细教程 – ESP8266继电器MQTTVUE 实现远程开关灯 超详细教程 – ESP8266继电器MQTTVUE 实现远程开关灯 接线图 NC(通常闭合)与COM(公共)、NO(通常开放)与COM 是继电器引脚的不同配置,用于不…...

Android中级——四大组件工作过程
四大组件工作过程 ActivityServicestartService()过程bindService()过程 BroadcastReceiver注册过程发送和接收过程 ContentProvider Activity startActivity()最终都会调用到startActivityForResult() public void startActivityForResult(RequiresPermission Intent intent…...

【RabbitMQ】RabbitMQ 服务无法启动。系统出错。发生系统错误 1067。进程意外终止。
问题描述 RabbitMQ 服务无法启动。 rabbitmq-service.bat startRabbitMQ 服务正在启动 . RabbitMQ 服务无法启动。系统出错。发生系统错误 1067。进程意外终止。原因分析 RabbitMQ和Erlang版本不匹配。 解决方案 查询并安装RabbitMQ版本对应Erlang版本 https://www.rabbitm…...
如何理解attention中的Q、K、V?
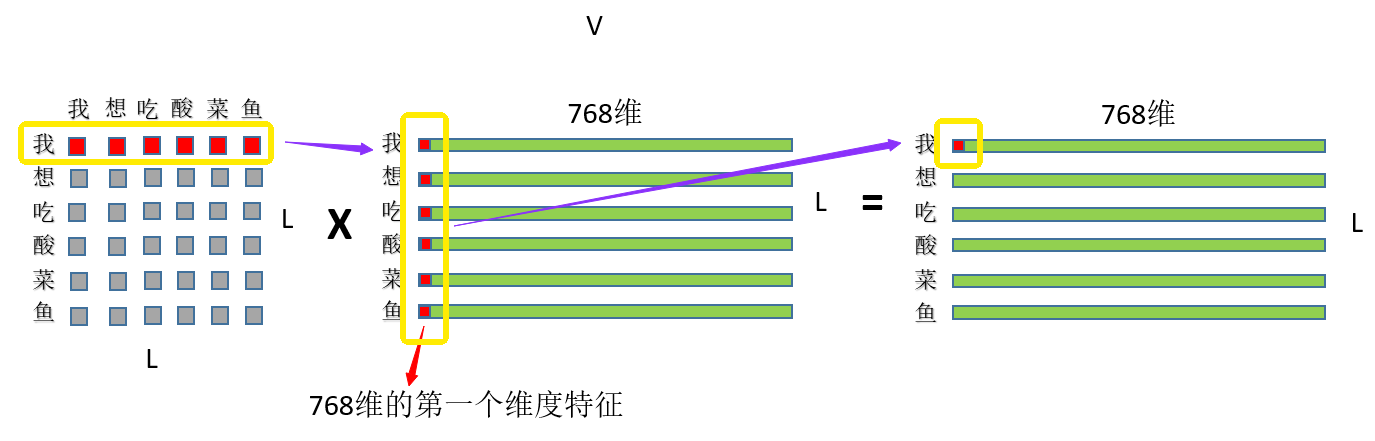
y直接用torch实现一个SelfAttention来说一说: 1、首先定义三哥线性变换,query,key以及value: class BertSelfAttention(nn.Module):self.query nn.Linear(config.hidden_size, self.all_head_size)#输入768,输出768…...

Redis----取代RabbitMq 和 Kafka的解决方案
背景 已知rabbitmq和kafka作为消息中间件来给程序之间增加异步消息传递功能,这两个中间件都是专业的,功能也很强,但是有的时候过于复杂,对于只有一组消费者的消息队列,使用Redis 就可以轻松搞定。 异步消息队列 读者…...
动态规划之连续乘积最大子数组 连续和最大子数组
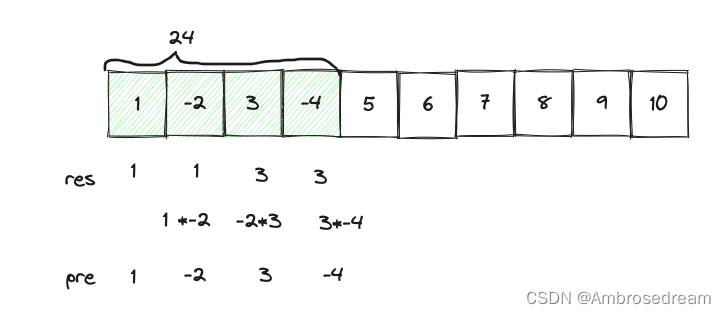
一. 连续和最大子数组 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。 子数组 是数组中的一个连续部分。 示例 1: 输入:nums [-2,1,-3,4,-1,2,1,-5,…...

keil在点击debug无法运行(全速运行)
1、今天发现我之前可以debug的程序,在板子上无法debug了,打断点完全没用 2、换了电脑,带板子过去也这样,之前可以运行的代码都debug不了 3、按照网上的方法,都不行,全速运行,单步执行都是灰色…...

go语言-协程
mOS结构体 每一种操作系统不同的线程信息 g给g0栈给g0协程内存中分配的地址,记录函数跳转信息, 单线程循环 0.x版本 1.0版本 多线程循环 操作系统并不知道Goroutine的存在 操作系统线程执行一个调度循环,顺序执行Goroutine 调度循环非常…...

如何伪造http头,让后端认为是本地访问
0x00 前言 这个知识点纯粹就是为了ctf准备的,很少有系统会出现这种情况。 0x01 正文 1.host头 如果后端从host取值来判断是否是本地就可以通过此方法进行绕过: host: 127.0.0.12.X-Forwarded-For X-Forwarded-For(XFF)是用来…...
视频剪辑音效处理软件有哪些?视频剪辑软件那个好用
音效是视频剪辑的重要部分,能起到画龙点睛的作用。在短视频平台中,一段出彩的音效能将原本平平无奇的视频变得生动有趣。那么,视频剪辑音效处理软件有哪些?本文会给大家介绍好用的音效处理软件,同时也会介绍视频剪辑音…...

搭建STM32F407的Freertos系统(基于STM32CubeMX)
本人长期开发Linux、Windows上应用软件,一直以来MCU开发有所接触,但较少(最近项目需要,小公司么,都得会,被逼的),好在有STM32CubeMX这样工具,貌似就是我想要的工具。 本次…...
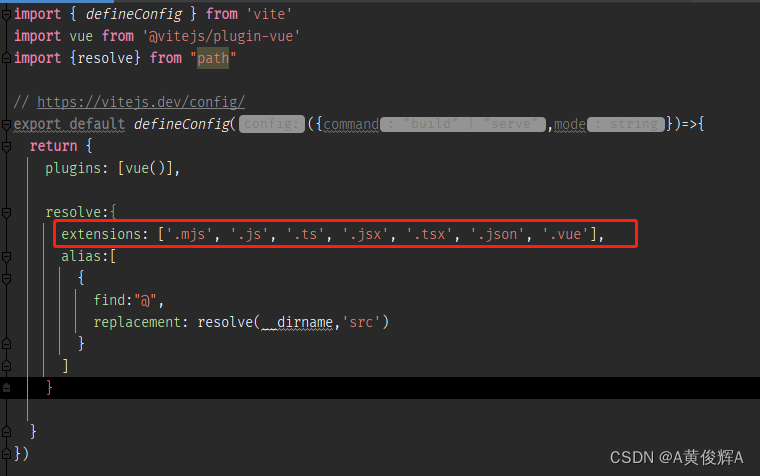
vite 配置自动补全文件的后缀名
vite 不建议自动补全,文件的后缀名的 const Home ()>import("/views/Home.vue");文件是必须要加上 .vue 的后缀名的 如果 想要像 webpack 一样的不用写, 可以在vite.config.js中配置如下就可以了...

基于Spring Boot的人才公寓管理系统设计与实现(Java+spring boot+MySQL)
获取源码或者论文请私信博主 演示视频: 基于Spring Boot的人才公寓管理系统设计与实现(Javaspring bootMySQL) 使用技术: 前端:html css javascript jQuery ajax thymeleaf 微信小程序 后端:Java spring…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...
