【数据结构】 二叉树面试题讲解->贰
文章目录
- 🌏引言
- 🎄[二叉树遍历](https://www.nowcoder.com/practice/4b91205483694f449f94c179883c1fef?tpId=60&&tqId=29483&rp=1&ru=/activity/oj&qru=/ta/tsing-kaoyan/question-ranking)
- 🐱👤题目描述:
- 📌输入描述:
- 📌输出描述:
- 🐱🐉示例:
- 🐱👓思路解析:
- 🐱🏍完整代码实现:
- 🌳[二叉树的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/description/)
- 🐱👤题目描述:
- 🐱🐉示例:
- 📌示例一
- 📌示例二
- 🐱👓思路解析
- 🚩思路一
- 🚩思路二
- 🐱🏍代码实现:
- 🎈思路一代码实现
- 🎈思路二代码实现
- 🎍[从前序与中序遍历序列构造二叉树](https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/)
- 🐱👤题目描述
- 🐱🐉示例:
- 🐱👓思路解析:
- 🐱🏍代码实现:
- 🌲拓展——[从中序与后序遍历序列构造二叉树](https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/%E3%80%81)
- ⭕总结
🌏引言
二叉树的操作算法是笔试面试中较为常见的题目。
本文将着重介绍平时面试中常见的关于二叉树的应用题目,马上要进行秋招了。希望对你们有帮助 _😀

🎄二叉树遍历
🐱👤题目描述:
编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。 例如如下的先序遍历字符串: ABC##DE#G##F### 其中“#”表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
📌输入描述:
输入包括1行字符串,长度不超过100。
📌输出描述:
可能有多组测试数据,对于每组数据, 输出将输入字符串建立二叉树后中序遍历的序列,每个字符后面都有一个空格。 每个输出结果占一行。
🐱🐉示例:
输入: abc##de#g##f###
输出:c b e g d f a
🐱👓思路解析:
首先我们先来看一下示例输入的二叉树的形状

我们首先需要做的是创建一个二叉树类,用于建立一个新的二叉树
class TreeNode1 {char val;TreeNode1 left;TreeNode1 right;TreeNode1() {}TreeNode1(char val) {this.val = val;}TreeNode1(char val, TreeNode1 left, TreeNode1 right) {this.val = val;this.left = left;this.right = right;}
}
接下来我们需要
- 依旧采用递归的思想
- 对字符串的每一个元素进行遍历,并进行判断
- 在遍历时,我们创建一个静态变量为size,此后每遍历一个元素,size就++
- 若不为’#',则该结点设为根节点
- 并且size++;
- 然后因为是前序遍历,所以根节点后面应该是左子树,然后是右子树
- 若为’#',则该节点为null,我们只需要size++即可
- 最后返回该结点就好
代码实现如下:
public static TreeNode1 creatTree(String str) {TreeNode1 root = null;if (str.charAt(i) != '#') {root = new TreeNode1(str.charAt(i));i++;root.left = creatTree(str);root.right = creatTree(str);} else {i++;}return root;}
然后根据题意我们还需要进行一个中序遍历,这里我就不做赘述了,又不懂的小伙伴可以去看一下博主对于【数据结构】二叉数的存储与基本操作的实现的讲解
实现如下:
public static void inorder(TreeNode1 root) {if (root == null) {return;}inorder(root.left);System.out.print(root.val + " ");inorder(root.right);}
}
🐱🏍完整代码实现:
import java.util.Scanner;
class TreeNode1 {char val;TreeNode1 left;TreeNode1 right;TreeNode1() {}TreeNode1(char val) {this.val = val;}TreeNode1(char val, TreeNode1 left, TreeNode1 right) {this.val = val;this.left = left;this.right = right;}
}
public class Main {public static int i = 0;public static void main(String[] args) {Scanner in = new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 casei = 0;String st = in.nextLine();TreeNode1 root = new TreeNode1();root = creatTree(st);inorder(root);}}public static TreeNode1 creatTree(String str) {TreeNode1 root = null;if (str.charAt(i) != '#') {root = new TreeNode1(str.charAt(i));i++;root.left = creatTree(str);root.right = creatTree(str);} else {i++;}return root;}public static void inorder(TreeNode1 root) {if (root == null) {return;}inorder(root.left);System.out.print(root.val + " ");inorder(root.right);}
}
🌳二叉树的最近公共祖先
🐱👤题目描述:
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode(int x) { val = x; }* }*/
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {}🐱🐉示例:
📌示例一
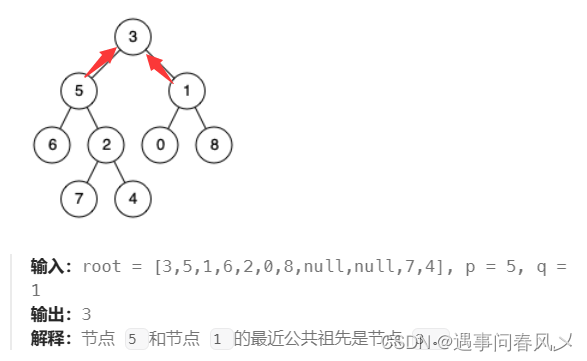
📌示例二
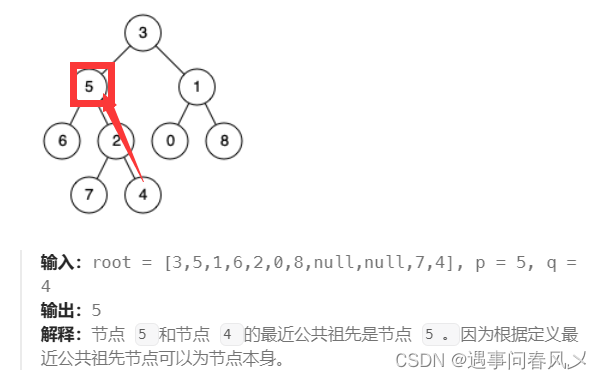
🐱👓思路解析
本题博主提供两种解题思路
🚩思路一
我们发现:
- 如果p,q不是根节点,且p,q一个在左子树被找到,一个在右子树被找到
- 那么该根节点为最近公共祖先
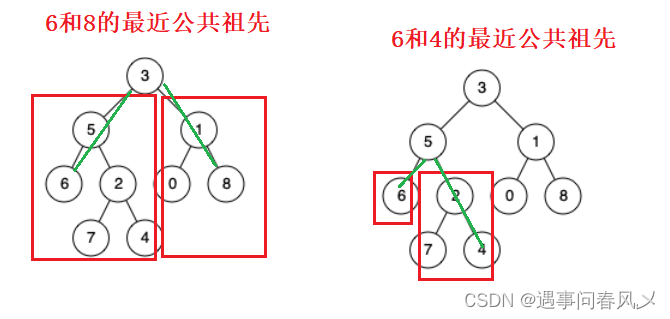
- 若该根节点为p或者q,那么自身则为最近祖先

若最后都没有找到,说明没有,返回空
🚩思路二
我们建立两个栈:
- 栈1用于存储找到p结点的路径
- 栈2用于存储找到q结点的路径

- 然后我们对两个栈求长度,把栈长度比较长的栈进行出栈,直到两个栈长度相等
- 然后同时出栈进行一一比对,相同则为p、q的最近公共祖先
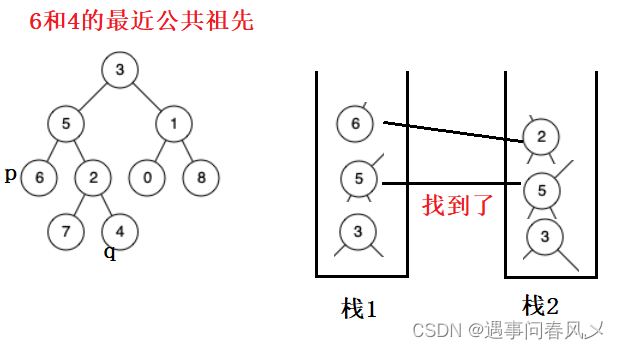
这种思路的解题难点在于如何找到p、q的路径并放入栈中,博主采用的做法如下: - 首先我们对二叉树与所找p、q结点进行判断
- 若为空返回false
- 然后我们需要对当前根节点进行判断,若为我们要找的p或q
- 则返回true
- 若没有我们便对该根节点的左子树进行入栈并进行判断,若找到返回true
- 若没有找到则将该左子树进行出栈
- 然后对右子树进行同样操作
- 最后若都没找到,返回false
然后我们只需要对两栈元素进行出栈进行比对就好了,最先相等的就为我们的最近公共祖先
🐱🏍代码实现:
🎈思路一代码实现
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode(int x) { val = x; }* }*/
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if(p == root || q == root) {return root;}if(root == null) {return null;}TreeNode l = lowestCommonAncestor(root.left,p,q);TreeNode r = lowestCommonAncestor(root.right,p,q);if(l != null && r != null) {return root;} else if(l != null) {return l;} else if(r != null) {return r;}return null;}
}
🎈思路二代码实现
class Solution {public boolean getPath(TreeNode root, TreeNode node,Deque<TreeNode> stack) {if(root == null || node == null)return false;stack.push(root);//放完之后 要检查if(root == node) return true;boolean ret1 = getPath(root.left,node,stack);if(ret1) return true;boolean ret2 = getPath(root.right,node,stack);if(ret2) return true;stack.pop();return false;}public TreeNode lowestCommonAncestor2(TreeNode root, TreeNode p, TreeNode q) {//1、两个栈当中 存储好数据Deque<TreeNode> stack1 = new LinkedList<>();getPath(root,p,stack1);Deque<TreeNode> stack2 = new LinkedList<>();getPath(root,q,stack2);//2、判断栈的大小int size1 = stack1.size();int size2 = stack2.size();if(size1 > size2) {int size = size1-size2;while (size != 0) {stack1.pop();size--;}}else {int size = size2-size1;while (size != 0) {stack2.pop();size--;}}//栈里面数据的个数 是一样的while (!stack1.isEmpty() && !stack2.isEmpty()) {if(stack1.peek() != stack2.peek()) {stack1.pop();stack2.pop();}else {return stack1.peek();}}return null;}
}
🎍从前序与中序遍历序列构造二叉树
🐱👤题目描述
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode buildTree(int[] preorder, int[] inorder) {}
}
🐱🐉示例:

🐱👓思路解析:
我们知道前序遍历里面第一个存储的是我们的根节点
那我们就可以在我们中序遍历中找到该结点,则该结点两边就为该根节点的左右子树
对于任意一颗树而言,前序遍历的形式总是
[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]
即根节点总是前序遍历中的第一个节点。而中序遍历的形式总是
[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]
只要我们在中序遍历中定位到根节点,那么我们就可以分别知道左子树和右子树中的节点数目。由于同一颗子树的前序遍历和中序遍历的长度显然是相同的,因此我们就可以对应到前序遍历的结果中,对上述形式中的所有左右括号进行定位。
这样以来,我们就知道了左子树的前序遍历和中序遍历结果,以及右子树的前序遍历和中序遍历结果,我们就可以递归地对构造出左子树和右子树,再将这两颗子树接到根节点的左右位置。
我们的做法是这样的
-
我们对前序遍历结果进行下标利用下标 i 遍历,并放入到二叉树中
-
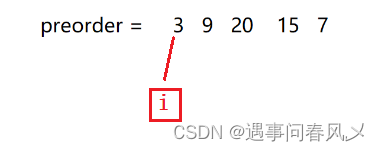
-
对中序遍历的元素设两个下标,一个记录最左边,一个记录最右边
-
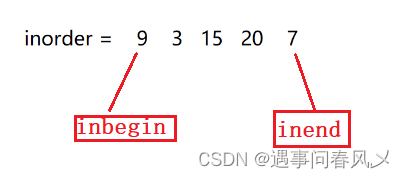
-
对前序遍历里的每一个元素我们会在中序遍历里进行查找,找到后
-
我们的inbegin与inend在左右子树里又会有新的指向
-
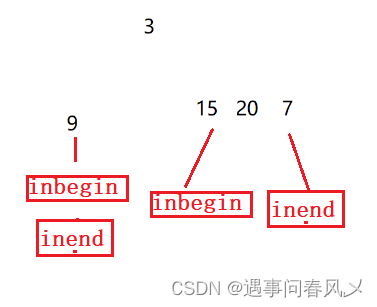
-
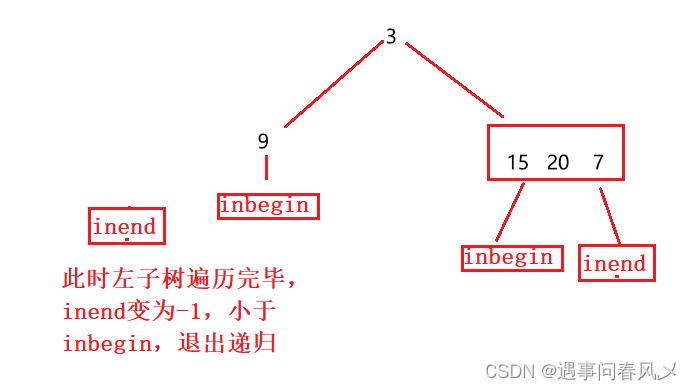
然后我们利用递归的思想,对所有元素进行遍历
-
结束条件为inend < inbengin
-
🐱🏍代码实现:
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int i = 0;public TreeNode buildTree(int[] preorder, int[] inorder) {return buildTreeChild(preorder,inorder,0,inorder.length-1);}public TreeNode buildTreeChild(int[] preorder, int[] inorder,int inbegin,int inend) {if(inbegin > inend) {return null;}TreeNode root = new TreeNode(preorder[i]);//找到当前根,在中序遍历的位置int rootIndex = findIndex(inorder,inbegin,inend,preorder[i]);i++;root.left = buildTreeChild(preorder,inorder,inbegin,rootIndex-1);root.right = buildTreeChild(preorder,inorder,rootIndex+1,inend);return root;}private int findIndex( int[] inorder,int inbegin,int inend, int key) {for(int i = inbegin;i <= inend; i++) {if(inorder[i] == key) {return i;}}return -1;}
}
🌲拓展——从中序与后序遍历序列构造二叉树
与从前序与中序遍历序列构造二叉树实现类似,这里不再做过多赘述
代码实现:
class Solution2 {public int i = 0;public TreeNode buildTree(int[] inorder, int[] postorder) {i = postorder.length-1;return buildTreeChild(postorder,inorder,0,inorder.length-1);}public TreeNode buildTreeChild(int[] postorder, int[] inorder,int inbegin,int inend) {if(inbegin > inend) {return null;}TreeNode root = new TreeNode(postorder[i]);//找到当前根,在中序遍历的位置int rootIndex = findIndex(inorder,inbegin,inend,postorder[i]);i--;root.right = buildTreeChild(postorder,inorder,rootIndex+1,inend);root.left = buildTreeChild(postorder,inorder,inbegin,rootIndex-1);return root;}private int findIndex( int[] inorder,int inbegin,int inend, int key) {for(int i = inbegin;i <= inend; i++) {if(inorder[i] == key) {return i;}}return -1;}}⭕总结
关于《【数据结构】 二叉树面试题讲解->贰》就讲解到这儿,感谢大家的支持,欢迎各位留言交流以及批评指正,如果文章对您有帮助或者觉得作者写的还不错可以点一下关注,点赞,收藏支持一下!
相关文章:

【数据结构】 二叉树面试题讲解->贰
文章目录 🌏引言🎄[二叉树遍历](https://www.nowcoder.com/practice/4b91205483694f449f94c179883c1fef?tpId60&&tqId29483&rp1&ru/activity/oj&qru/ta/tsing-kaoyan/question-ranking)🐱👤题目描述&#…...

C和SystemVerilog联合仿真
想要联合仿真一个c程序和verilog表示的硬件,可以用如下方法(DPI): 先写一个.c文件funcs.c #include <stdio.h> #include "svdpi.h"extern int sayHello();void something() {printf("something\n");s…...

15-mongodb
一、 MongoDB 简介 1 什么是 MongoDB MongoDB 是一个基于分布式文件存储的数据库。由 C语言编写。在为 WEB 应用提供可扩展的高性能数据存储解决方案。 MongoDB 是一个介于关系数据库和非关系数据库之间的产品,是非关系数据库当中功能最丰富,最像关系…...

CSS学习笔记02
CSS笔记02 美化网页元素 为什么要美化网页 目的: 有效的传递页面信息美化网页、页面漂亮、才能吸引用户突显页面的主题提高用户的体验 span标签 span标签是短语内容的通用行内容器,它本身并没有任何特殊语义。 通常我们使用span标签来把我们想要重…...

为什么Java接口可以多继承,而类不可以?
个人主页:金鳞踏雨 个人简介:大家好,我是金鳞,一个初出茅庐的Java小白 目前状况:22届普通本科毕业生,几经波折了,现在任职于一家国内大型知名日化公司,从事Java开发工作 我的博客&am…...

自动化信息收集工具 水泽 使用教程
自动化信息收集工具 水泽 使用教程 1.水泽简介&安装2.使用教程3.测试使用1.水泽简介&安装 一条龙服务,只需要输入根域名即可全方位收集相关资产,并检测漏洞。也可以输入多个域名、C段IP等 开发语言:Python3 水泽下载地址 安装前置准备: 当前用户对该目录有写权…...
“信息安全管理与评估”理论技能答案)
2023年全国职业院校技能大赛(高等职业教育组)“信息安全管理与评估”理论技能答案
理论技能与职业素养(100分) 2023年全国职业院校技能大赛(高等职业教育组) “信息安全管理与评估”理论技能 【注意事项】 1.理论测试前请仔细阅读测试系统使用说明文档,按提供的账号和密码登录测试系统进行测试&am…...
MATLAB 动态图GIF
MATLAB 动态图GIF 前言一、创建动态图(动态曲线、动态曲面)1. 创建动画曲线(MATLAB animatedline函数)2. 创建动画曲面 二. 保存动态图三、完整示例1. 动态曲线( y s i n ( x ) ysin(x) ysin(x))2. 动态曲…...
ChatGPT⼊门到精通(4):ChatGPT 为何⽜逼
⼀、通⽤型AI 在我们原始的幻想⾥,AI是基于对海量数据的学习,锻炼出⼀个⽆所不知⽆所不能的模 型,并借助计算机的优势(计算速度、并发可能)等碾压⼈类。 但我们⽬前的AI,不管是AlphaGo还是图像识别算法&am…...
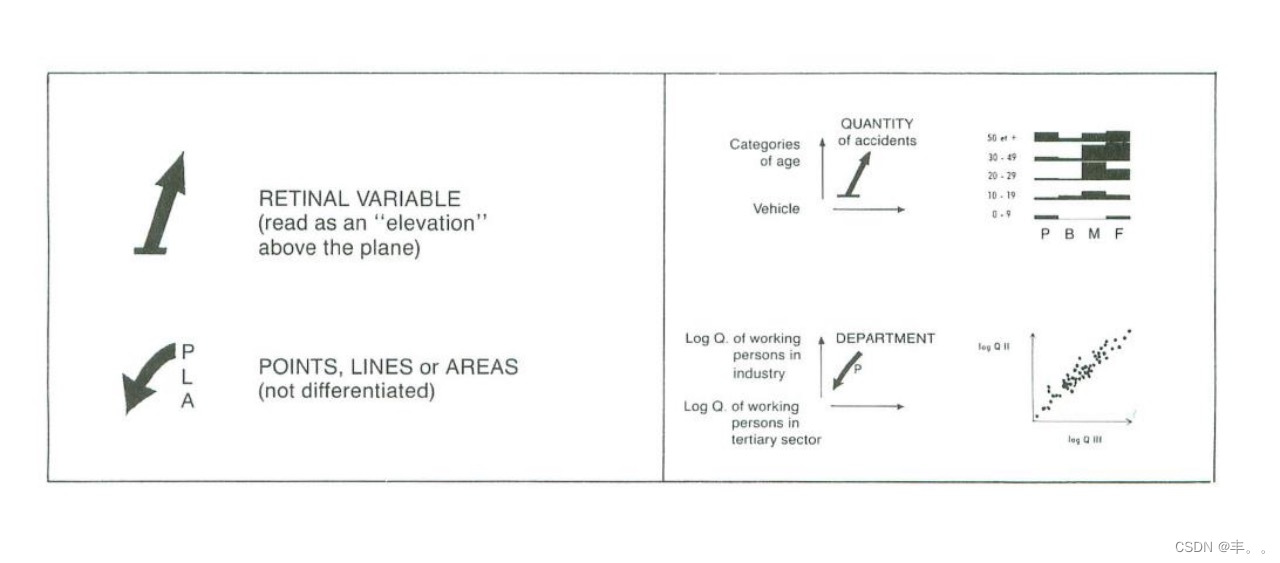
数据分析基础-数据可视化学习笔记03-可视化的符号与表示-图形符号学
概念 图型符号学(Cartographic Symbolization)是地图学领域中的一个重要概念,涉及到如何使用不同的符号、颜色、图案和标记来在地图上表示地理信息和数据。图型符号学旨在传达地理信息,使得地图能够清晰、有效地传达各种空间数据…...
)
暴力递归转动态规划(四)
题目 规定1对应A、2对应B、3对应C…26对应Z,那么一个数字字符串比如"111",就可以转化为:“AAA”、“KA"或"AK”,给定一个数字字符组成的字符串str,返回有多少种转化结果。 解释一下,字…...

大数据项目实战(Sqoop安装)
一,搭建大数据集群环境 1.4 Sqoop安装 1.sqoop安装 (1)上传安装包 (2)解压安装包 tar -zxvf sqoop-1.4.6.bin__hadoop-2.0.4-alpha.tar.gz -C /export/servers (3)重命名 mv sqoop-1.4.6.b…...

android——spinner下拉弹窗、popupwindow下拉弹窗列表
一、spinner下拉弹窗 效果图如下: adapter的代码: package com.yaona.spinnerimport android.R import android.content.Context import android.graphics.Color import android.view.LayoutInflater import android.view.View import android.view.Vie…...

【阿里淘天】淘天20230824真题一、二 <模拟、双指针>
一、 题目描述: 小红有一个01字符串,她可以进行最多k次提作,每次操作可以交换相邻的两个字符,问可以得到的字典序最小的字符串是什么 输入描述: 一行两个整数 n 和 k,表示字符串的长度和可以进行的操作…...

Java注解和反射
注解(Java.Annotation) 什么是注解(Annotation)? Annotation是从JDK5.0开始引入的新技术 Annotation的作用: 不是程序本身,可以对程序作出解释(这一点和注释(comment)没什么区别)可以被其他程序(比如:编译器等)读取Annotation的…...

【Docker】01-Centos安装、简单使用
参考教程: https://www.bilibili.com/video/BV1Qa4y1t7YH/?p5&spm_id_frompageDriver&vd_source4964ba5015a16eb57d0ac13401b0fe77 什么是Docker? Docker是一种开源的容器化平台,用于构建、打包、部署和运行应用程序。它通过使用容…...

k8s之存储篇---数据卷Volume
数据卷概述 Kubernetes Volume(数据卷)主要解决了如下两方面问题: 数据持久性:通常情况下,容器运行起来之后,写入到其文件系统的文件暂时性的。当容器崩溃后,kubelet 将会重启该容器ÿ…...

博流RISC-V芯片JTAG debug配置与运行
文章目录 1、Windows下安装与配置2、Linux下安装与配置3、芯片默认 JTAG PIN 列表4、命令行运行JTAG5、Eclipse下使用JTAG 1、Windows下安装与配置 CKLink 驱动安装 Windows版驱动下载地址: https://occ-oss-prod.oss-cn-hangzhou.aliyuncs.com/resource//1666331…...

[国产MCU]-W801开发实例-UART控制器
UART控制器 文章目录 UART控制器1、UART控制器介绍2、UART驱动API介绍3、UART使用示例本文将详细如何使用W801的UART模块。 1、UART控制器介绍 UART是一种通用串行 数据总线 ,用于 异步通信 。该总线支持双向通信,可以实现 全双工传输 和接收。 W801 共 6组普通 UART口,通…...

OpenCV(九):LUT查找表
LUT(Look-Up Table)查找表是OpenCV中一种常用的图像处理方法,用于对图像进行像素级别的颜色映射或图像增强操作。LUT查找表可以实现快速、高效的颜色转换和像素操作,尤其在处理大量像素的情况下具有优势。以下是关于OpenCV LUT查找…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
