【leetcode 力扣刷题】数学题之计算次幂//次方:快速幂
利用乘法求解次幂问题—快速幂
- 50. Pow(x, n)
- 372. 超级次方
50. Pow(x, n)
题目链接:50. Pow(x, n)
题目内容:

题目就是要求我们去实现计算x的n次方的功能函数,类似c++的power()函数。但是我们不能使用power()函数直接得到答案,那样这道题就失去了考察的意义。
前面提到乘法a*b可以看作是b个a相加,用加法来完成乘法;x的n次方,就是n个x相乘,那么同样可以用乘法来代替次幂计算,我们称之为快速幂。比如5^7,就是7个5相乘,快速幂的过程如下:

第一轮是乘以5,第二轮乘以5*5,第三轮乘以(5*5)*(5*5),也就是每一轮乘的数都在加倍,这样就能够在log^n的时间复杂度内完成x^n的计算。代码实现如下(C++):
class Solution {
public:double myPow(double x, int n) {//先处理特殊情况if(x == 0) return 0.0;if(x == 1) return 1.0;if(n == 0) return 1.0;bool flage = false;long _n = n;//如果n是负数,x^n = 1/(x^|n|)if(_n < 0){flage = true;_n = -_n;}double ans = 1;double mul = x;//快速幂主体过程while(_n){ if(_n&1) //如果n末位为1,就乘以mulans *= mul; mul *= mul; //mul翻倍_n >>= 1; //n右移一位}return flage ? 1.0/ans : ans; //判断是否需要变成倒数}
};
372. 超级次方
题目链接:372. 超级次方
题目内容:

看起来和上一题是差不多的,但是由于b是一个非常大的正整数,以数组形式给出[1,0,3,4]就表示1034【末位是个位,然后是十位,然后是百位,最前面的是最高位】。其中1 <= b.length <= 2000说明b可以达到10^1999的程度,根本没法用double、long long等数据类型来存储这么大的数,所以在运算过程中也不能直接把b转换成一个数或者每一位转换成一个数,需要其他方法:

将每一位b[i]的数值b[i]*10^(m-1-i)【其中m是b.length】分解成b[i]和10^(m-1-i)两部分,每次先求a^(10^(m-1-i))得到A,再求A^b[i]。a^(10^(m-1-i))随着i的减小越来越大,但是可以看作是上一轮的A^10。
由于每次次幂结果都要mod 1337,所以结果是不会溢出的,a^(10^(m-1-i))每一次用上一轮的A^10来表示就解决了b很大的问题。另外需要注意的是(a*b) mod k =( (a mod k) * (b mod k) ) mod k。
a^(10^(m-1-i))和A^b[i]以及A^10都用快速幂求解。快速幂过程中根据(a*b) mod k =( (a mod k) * (b mod k) ) mod k加上求模操作。代码如下(C++):
class Solution {
public://快速幂long quick_pow(int a, int n){int ans = 1;int mul = a;while(n){if(n&1)//加上求模操作ans = ( (ans % 1337) * (mul % 1337)) % 1337;//mul也加上求模操作mul = ((mul % 1337) * (mul % 1337)) % 1337;n>>=1;}return ans;}int superPow(int a, vector<int>& b) {int ans = 1; for(int j = b.size() - 1; j >= 0; j--){ans =( (ans % 1337) * (quick_pow(a,b[j]) % 1337) ) % 1337;//每次a都在上一次的基础上,变成其10次方a = quick_pow(a, 10);}return ans;}
};
相关文章:

【leetcode 力扣刷题】数学题之计算次幂//次方:快速幂
利用乘法求解次幂问题—快速幂 50. Pow(x, n)372. 超级次方 50. Pow(x, n) 题目链接:50. Pow(x, n) 题目内容: 题目就是要求我们去实现计算x的n次方的功能函数,类似c的power()函数。但是我们不能使用power()函数直接得到答案,那…...
【核心复现】基于改进灰狼算法的并网交流微电网经济优化调度(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
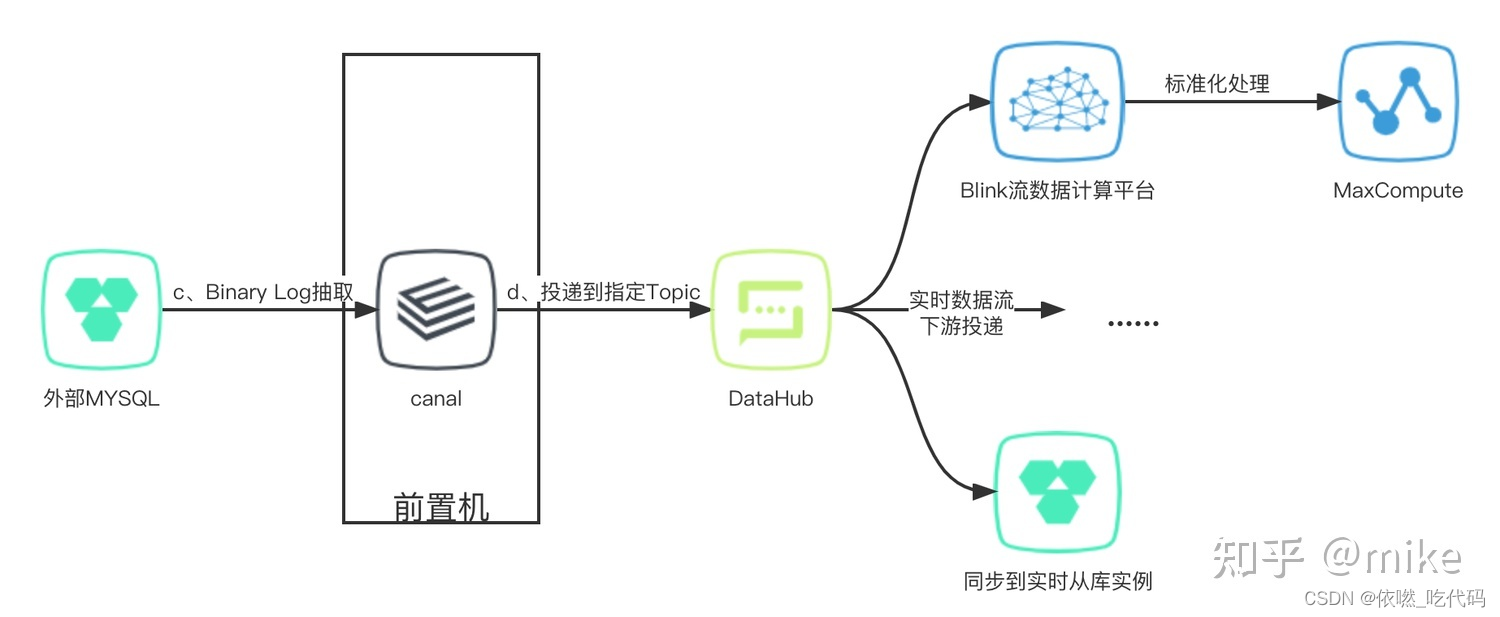
Cannal监听binlog
文章目录 一、canal概念二、canal使用场景四、Canal工作原理Mysql主从复制原理 binlog中的二进制日志binlog格式选择 Canal消费方式应用实践总结 一、canal概念 canal是用java开发的基于数据库增量日志解析,提供增量数据订阅&消费的中间件。目前,ca…...
从零开发JavaWeb入门项目--十天掌握
原文网址:从零开发JavaWeb入门项目--十天掌握_IT利刃出鞘的博客-CSDN博客 简介 这是一个靠谱的JavaWeb入门项目实战,名字叫蚂蚁爱购。从零开发项目,视频加文档,十天就能学会开发JavaWeb项目,教程路线是:搭…...

数据结构——哈希表
哈希表 这里没有讲哈希表底层的概念,什么转红黑树,什么链表的,这篇文章主要讲的是如何用C实现哈希表,以及哈希表的基本概念。后面我会出一篇文章来讲C中hashmap中的底层逻辑的知识。 哈希表的概念 哈希表是一种数据结构࿰…...

Kafka3.0.0版本——手动调整分区副本示例
目录 一、服务器信息二、启动zookeeper和kafka集群2.1、先启动zookeeper集群2.2、再启动kafka集群 三、手动调整分区副本3.1、手动调整分区副本的前提条件3.2、手动调整分区副本的示例需求3.3、手动调整分区副本的示例 一、服务器信息 四台服务器 原始服务器名称原始服务器ip节…...

玩客云 线刷Armbian 搭配Alist 阿里云盘 Jellyfin NovaVideoPlayer搞电视墙
啰嗦的背景 喜欢看电影,买了个投影仪,是这一切折腾的开端。 投影仪虽然有当贝系统,但是想看的电影总是需要**电视会员,那我肯定是不用的。因为有爱腾优的会员,最开始都是使用手机投屏,当呗的投影仪好就好…...

9月1日,每日信息差
1、华大智造:已实现海外基因测序仪和测序试剂的量产,实现了海外基因测序仪和测序试剂的量产 2、邮储银行下调定存利率。价格表显示,整存整取,一年期存款年利率为1.58%,二年期年利率为1.85%,三年期年利率为…...

【大数据】Flink 详解(六):源码篇 Ⅰ
Flink 详解(六):源码篇 Ⅰ 55、Flink 作业的提交流程?56、Flink 作业提交分为几种方式?57、Flink JobGraph 是在什么时候生成的?58、那在 JobGraph 提交集群之前都经历哪些过程?59、看你提到 Pi…...
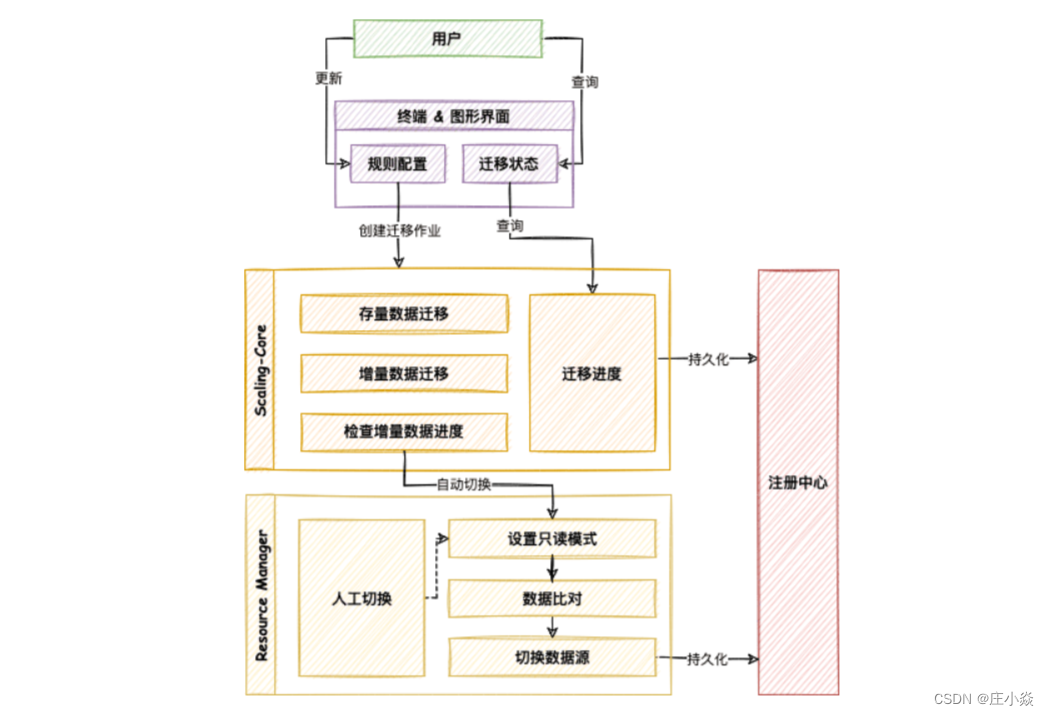
ShardingSphere——弹性伸缩原理
摘要 支持自定义分片算法,减少数据伸缩及迁移时的业务影响,提供一站式的通用弹性伸缩解决方案,是 Apache ShardingSphere 弹性伸缩的主要设计目标。对于使用单数据库运行的系统来说,如何安全简单地将数据迁移至水平分片的数据库上…...

Linux项目自动化构建工具-make/Makefile
一、什么是make和makefile make是一条指令 Makefile是当前目录下的一个文件 二、makefile文件编写 依赖关系::前为要目标文件,后为其依赖的文件 依赖方法:用依赖文件生成目标文件的具体指令 简便写法: $:表示目标文件 $^:表示…...

Python爬虫实战:自动化数据采集与分析
在大数据时代,数据采集与分析已经成为了许多行业的核心竞争力。Python作为一门广泛应用的编程语言,拥有丰富的爬虫库,使得我们能够轻松实现自动化数据采集与分析。本文将通过一个简单的示例,带您了解如何使用Python进行爬虫实战。…...
视频智能分析平台EasyCVR安防视频汇聚平台助力森林公园防火安全的应用方案
一、研发背景 随着经济的发展和人们生活水平的提高,越来越多的人喜欢在周末去周边的森林公园旅游,享受大自然的美景,并进行野炊和烧烤等娱乐活动。然而,近年来由于烟蒂和烧烤碳渣等人为因素,森林公园火灾频繁发生。森…...

跨境做独立站,如何低成本引流?
大家都知道,海外的消费习惯与国内不同,独立站一向是海外消费者的最喜欢的购物方式之一,这也吸引了许多跨境商家开设独立站。 独立站不同于其他的第三方平台,其他平台可以靠平台自身流量来获得转化,而独立站本身没有流…...
leetcode55.跳跃游戏 【贪心】
题目: 给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 示例…...
探秘C语言扫雷游戏实现技巧
本篇博客会讲解,如何使用C语言实现扫雷小游戏。 0.思路及准备工作 使用2个二维数组mine和show,分别来存储雷的位置信息和排查出来的雷的信息,前者隐藏,后者展示给玩家。假设盘面大小是99,这2个二维数组都要开大一圈…...

Leetcode112. 路径总和
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 t…...

生成12位短id,自增且不连续,永不重复,不依赖数据库
基本思路: 设计模式:单例模式 是否加锁:是 synchronized 获取最后一次生成的时间戳值T0 限定初始时间为2023-08-01 00:00:00,获取当前时间时间戳T1,T1与初始时间的毫秒差值T2,转为16进制,转为字符串为r1,获取该字符串的长度L1…...

Zip压缩文件夹php打包函数代码
Zip压缩文件夹php打包函数代码,Zip相关函数是PHP的扩展功能,此函数可以直接复制使用。 以下是代码: <?php # 将文件夹的文件压缩到文件里 class Zip {/*** 将目标文件夹下的内容压缩到zip中(zip包含文件夹目录)* @param $sourcePath *文件夹路径 例: /home/test* @p…...

RISC-V交叉工具链riscv-gnu-toolchain编译
文章目录 1、下载2、编译1. 依赖安装2. 编译 3、运行 1、下载 $ sudo apt-get install git wget build-essential $ git clone https://github.com/riscv-collab/riscv-gnu-toolchain $ git checkout 2023.06.02注意上面 clone 的仓库,我们称其为构建脚本仓库&…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...
