数据结构体--5.0图
目录
一、定义
二、图的顶点与边之间的关系
三、图的顶点与边之间的关系
四、连通图
五、连通图的生成树定义
一、定义
图(Graph)是由顶点的又穷非空集合合顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V表示图G中定点的集合,E是图G中边的集合。
——线性表中我们把数据元素叫元素,树中叫结点,在图中数据元素我们则称之为定点(Vertex)。
——线性表可以没有数据元素,称为空表,树中可以没有结点,叫做空树,而图中的定点集合是有穷非空的。(国外是允许空的)
——线性表中,相邻的数据元素之间具有线性关系,数据结构中,相邻两层的结点具有层次关系,而图结构中,任意两个顶点之间都可能有关系,定点之间的逻辑关系用边来表示,边集是可以为空的。
1、无向边:若顶点Vi到Vj之间的边没有方向,则称这条边为无向边(Edge),用无序偶(Vi,Vj)来表示。

上图G1是一个无向图,G1={V1,E1},其中
——V1 = {A,B,C,D}
——E1 = {(A,C),(B,C),(C,D),(D,A),(A,C)}
2、有向边:若从定点Vi到Vj的边有方向,则称这条边为有向边,也成为弧(Arc),用有序偶<vi,Vj>来表示,Vi称为弧尾,Vj称为弧头。
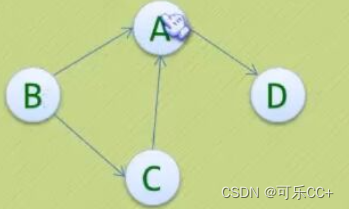
上图G2是一个有向图,G2={V2,E2},其中
——V2 = {A,B,C,D}
——E2 = {<B,A>,<B,C>,<C,A>,<A,D>}
二、图的顶点与边之间的关系
1、对于无向图G=(V,E),如果边(V1,V2)∈E,则称顶点V1和V2互为邻接点(Adjacent),即V1和V2相邻接。边(V1,V2)依附(incident)于顶点V1和V2,或者说边(V1,V2)与顶点V1和V2相关联。
2、顶点V的度(Degree)是和V相关联的边的数目,记为TD(V),如下图,顶点A与B互为邻接点,bian(A,B)依附于顶点A与B上,顶点A的度为3.

三、图的顶点与边之间的关系
1、对于有向图G=(V,E),如果边<V1,V2>∈E,则称顶点V1邻接到顶点V2,顶点V2邻接自顶点V1。
2、以顶点V为头的弧的数目称为V的入度(InDegree),记为ID(V),以V为尾的弧的数目称为V
的出度(OutDegree),记为OD(V),因此顶点V的度为TD(V)=ID(V)+OD(V)。
3、下图顶点A的入度是2,出度是1,所以顶点A的度是3。

四、连通图
1、在无向图G中,如果从顶点V1到顶点V2有路径,则称V1和V2是连通图,弱国对于图中任意两个顶点Vi和Vj都是连同的,则称G是连通图(ConnectedGraph)。
2、无向图中的极大连通子图称为连通分量。
3、注意:
——首先要是子图,并且子图是要连通的;
——连通子图含有极大顶点数;
——具有极大顶点数的连通子图包含依附于这些顶点的所有边。
4、在有向图G中,如果对于每一对Vi到V都存在路径,则称G是强连通图。
5、有向图中的极大强连通子图称为有向图的强连通分量。
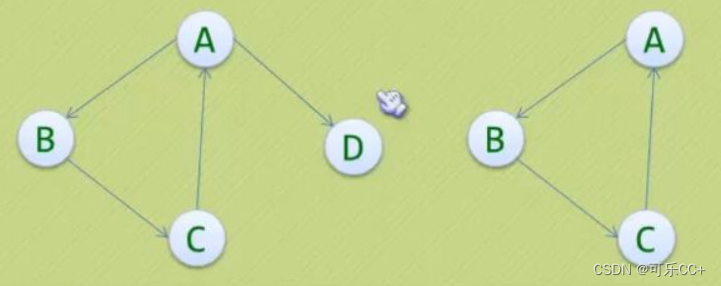
如下,左侧不是,右侧是
五、连通图的生成树定义
所谓的一个连通图的生成树是一个极小的连通子图,它含有图中全部的n个顶点,但只有足以构成一棵树的n-1跳边。
相关文章:

数据结构体--5.0图
目录 一、定义 二、图的顶点与边之间的关系 三、图的顶点与边之间的关系 四、连通图 五、连通图的生成树定义 一、定义 图(Graph)是由顶点的又穷非空集合合顶点之间边的集合组成,通常表示为:G(V,E&…...

深入剖析 Golang 程序启动原理 - 从 ELF 入口点到GMP初始化到执行 main!
大家好,我是飞哥! 在过去的开发工作中,大家都是通过创建进程或者线程来工作的。Linux进程是如何创建出来的? 、聊聊Linux中线程和进程的联系与区别! 和你的新进程是如何被内核调度执行到的? 这几篇文章就是…...
C语言——多文件编程
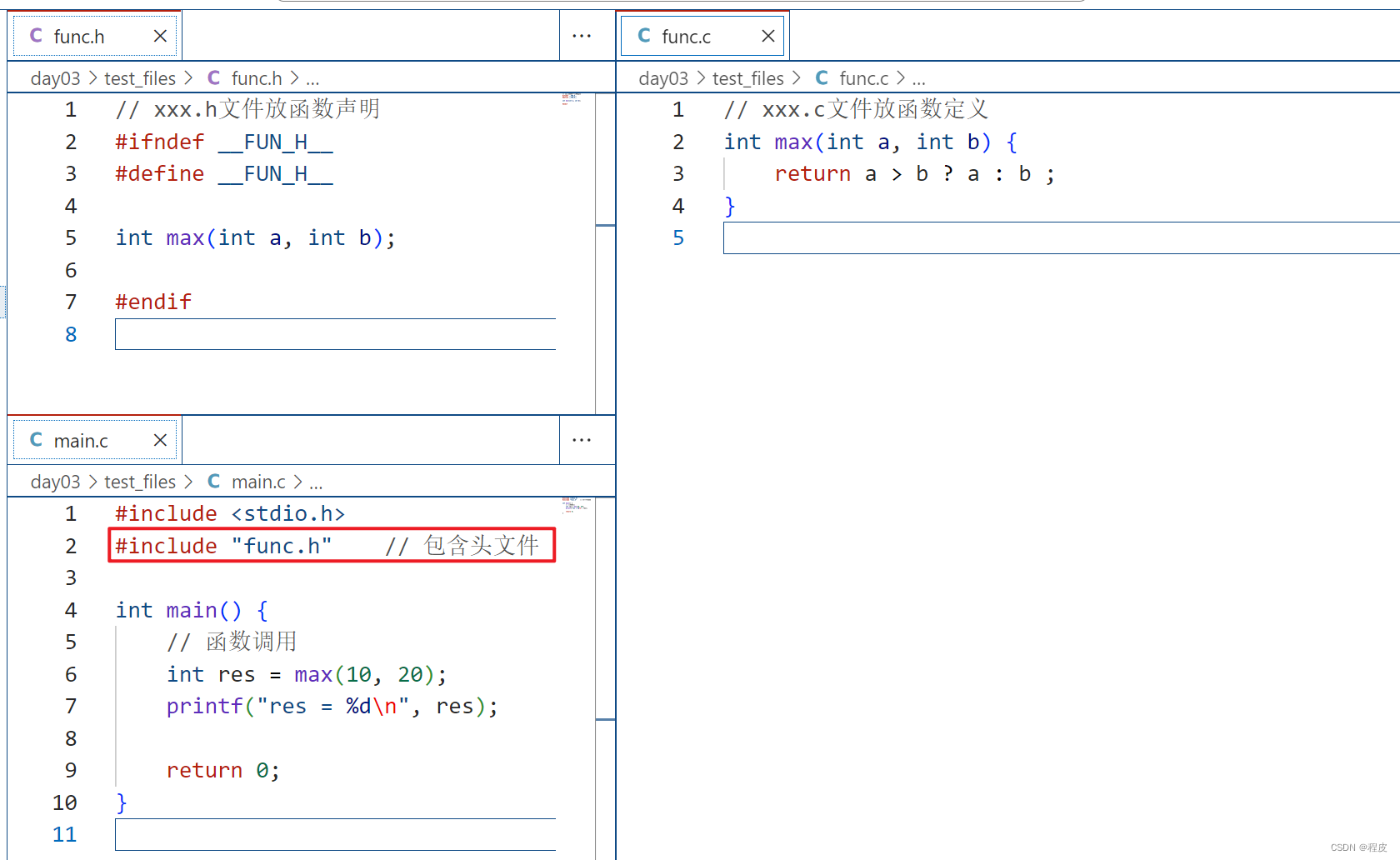
多文件编程 把函数声明放在头文件xxx.h中,在主函数中包含相应头文件在头文件对应的xxx.c中实现xxx.h声明的函数 防止头文件重复包含 当一个项目比较大时,往往都是分文件,这时候有可能不小心把同一个头文件 include 多次,或者头…...

Git学习part1
02.尚硅谷_Git&GitHub_为什么要使用版本控制_哔哩哔哩_bilibili 1.Git必要性 记录代码开发的历史状态 ,允许很多人同时修改文件(分布式)且不会丢失记录 2.版本控制工具应该具备的功能 1)协同修改 多人并行不悖的修改服务器端…...

2309C++均为某个类型
#include <常用> 构 A{空 f(){打印("啊");} }; 元<类 T>构 是点啊:假型{}; 元<>构 是点啊<A>:真型{}; 元<类 T>概念 是呀是点啊<T>::值;元<是呀...T>空 f(T&...t){(t.f(),...); }//均为元<类...T>要求 均为值&l…...

2023年打脸面试官之TCP--瞬间就懂
1.TCP 三次握手之为什么要三次呢?事不过三? 过程如下图: 先来解释下上述的各个标志的含义 序列号seq:占4个字节,用来标记数据段的顺序,TCP把连接中发送的所有数据字节都编上一个序号,第一个字节…...

设计模式-单例模式Singleton
单例模式 单例模式 (Singleton) (重点)1) 为什么要使用单例2) 如何实现一个单例2.a) 饿汉式2.b) 懒汉式2.c) 双重检查锁2.d) 静态内部类2.e) 枚举类2.f) 反射入侵2.g) 序列化与反序列化安全 3) 单例存在的问题3.a) 无法支持面向对象编程 单例模式 (Singleton) (重点) 一个类只…...

PPPoE连接无法建立的排查和修复
嗨,亲爱的读者朋友们!你是否曾经遇到过PPPoE连接无法建立的问题?今天我将为你详细解析排查和修复这个问题的步骤。 检查物理连接 首先,我们需要确保物理连接没有问题。请按照以下步骤进行检查: - 检查网线是否插好&…...

QT 发布软件基本操作
一、配置环境变量 找到Qt安装时的bin目录的路径:D:\Qt\Qt5.14.2\5.14.2\mingw73_64\bin,将目录拷贝至下述环境变量中。 打开计算机的高级系统设置 选中环境变量-->系统变量-->Path 点击编辑-->新建-->粘贴 二、生成发布软件的可执行程序 …...
CTFhub-SSRF-内网访问
CTFHub 环境实例 | 提示信息 http://challenge-8bf41c5c86a8c5f4.sandbox.ctfhub.com:10800/?url_ 根据提示,在url 后门添加 127.0.0.1/flag.php http://challenge-8bf41c5c86a8c5f4.sandbox.ctfhub.com:10800/?url127.0.0.1/flag.php ctfhub{a6bb51530c8f6be0…...

Cenos7安装小火车程序动画
运维Shell脚本小试牛刀(一) 运维Shell脚本小试牛刀(二) 运维Shell脚本小试牛刀(三)::$(cd $(dirname $0); pwd)命令详解 运维Shell脚本小试牛刀(四): 多层嵌套if...elif...elif....else fi_蜗牛杨哥的博客-CSDN博客 Cenos7安装小火车程序动画 一:替换…...

Node 执行命令时传参 process.argv
process 对象是一个全局变量,提供当前 Node.js 进程的有关信息,以及控制当前 Node.js 进程。 因为是全局变量,所以无需使用 require()。 process.argv 属性返回一个数组,这个数组包含了启动Node.js进程时的命令行参数,…...

【Vue】快速上手--Vue 3.0
什么是 Vue? Vue (发音为 /vjuː/,类似 view) 是一款用于构建用户界面的 JavaScript 框架。它基于标准 HTML、CSS 和 JavaScript 构建,并提供了一套声明式的、组件化的编程模型,帮助你高效地开发用户界面。无论是简单还是复杂的…...
PyTorch深度学习遥感影像地物分类与目标检测、分割及遥感影像问题深度学习优化实践技术应用
我国高分辨率对地观测系统重大专项已全面启动,高空间、高光谱、高时间分辨率和宽地面覆盖于一体的全球天空地一体化立体对地观测网逐步形成,将成为保障国家安全的基础性和战略性资源。未来10年全球每天获取的观测数据将超过10PB,遥感大数据时…...
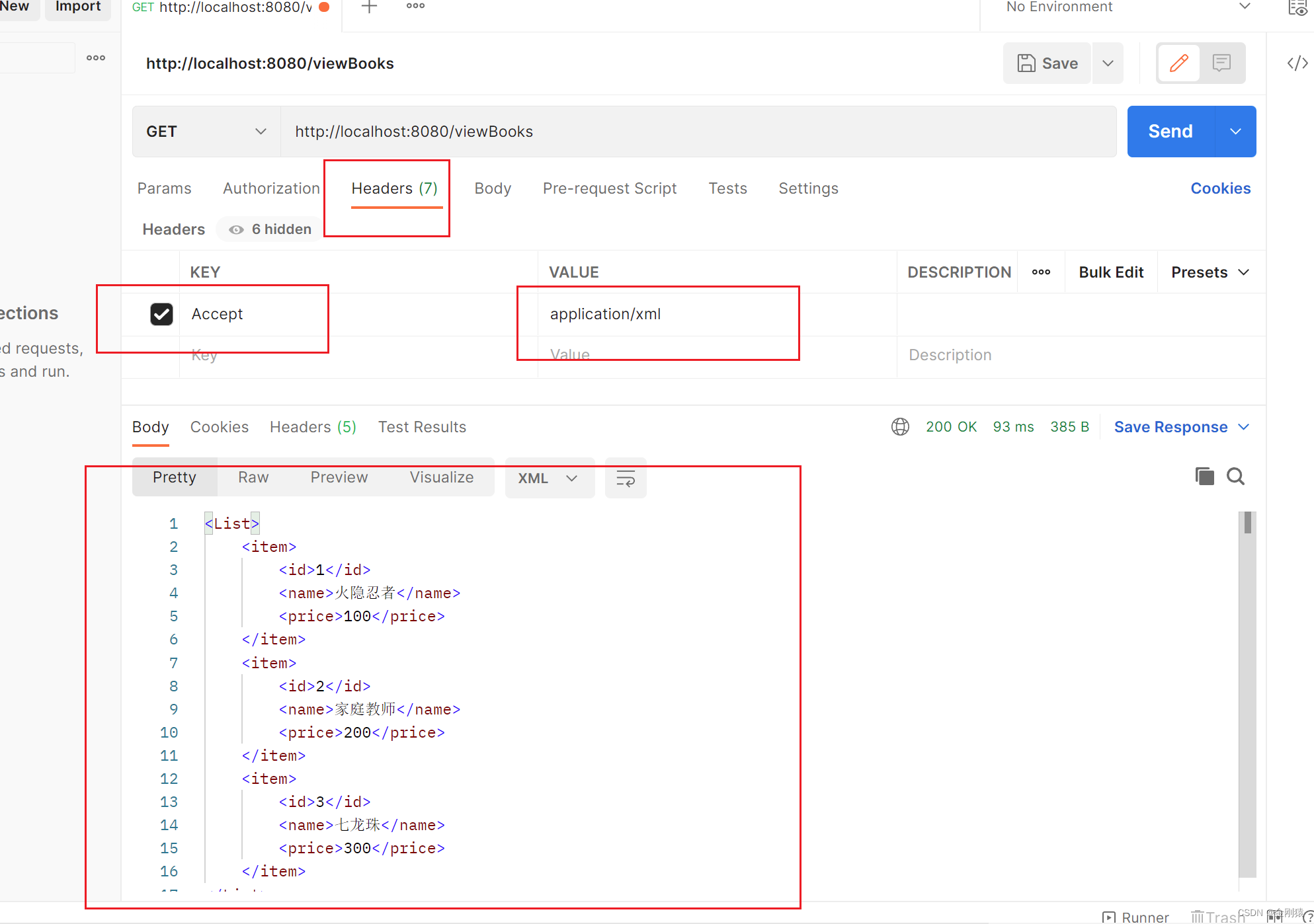
04、添加 com.fasterxml.jackson.dataformat -- jackson-dataformat-xml 依赖报错
Correct the classpath of your application so that it contains a single, compatible version of com.fasterxml.jackson.dataformat.xml.XmlMapper 解决: 改用其他版本,我没写版本号,springboot自己默认的是 2.11.4 版本 成功启动项目…...
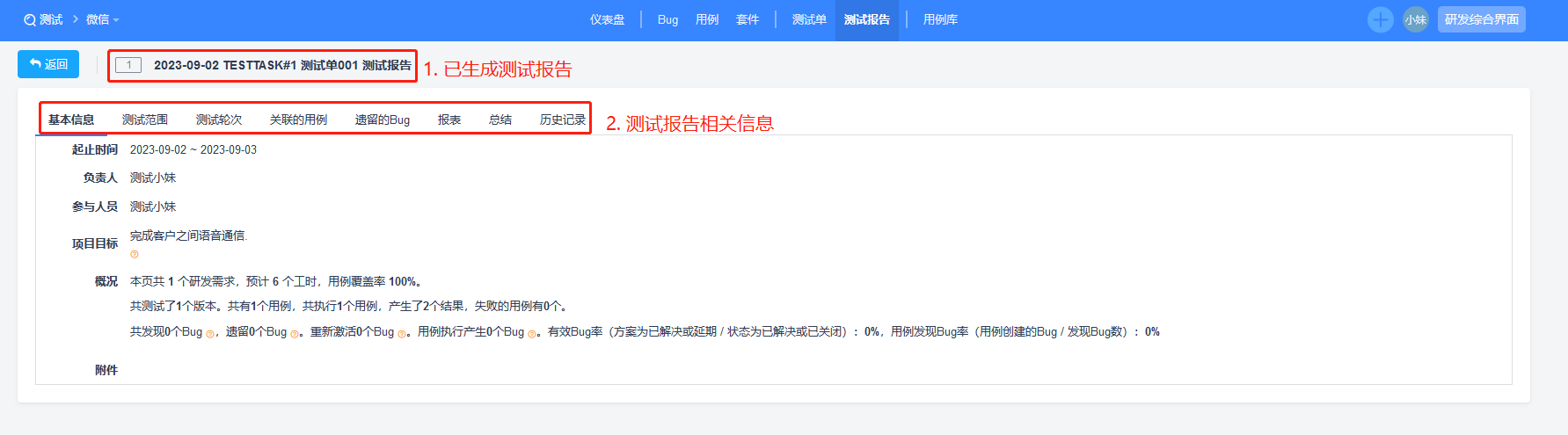
禅道项目管理系统 - 操作使用 (2023版)
1. 部门-用户-权限 新增部门 新增用户 设置权限 2. 项目集创建 项目集 - 添加项目集 3. 产品线创建 产品 - 产品线 4. 产品创建 产品 - 产品列表 - 添加产品 5. 产品计划创建 产品 - xx产品 - 计划 - 创建计划 我这里创建3个计划 (一期, 二期, 三期) 6. 研发需求 - 创建模块…...

C++的多重继承
派生类都只有一个基类,称为单继承(Single Inheritance)。除此之外,C++也支持多继承(Multiple Inheritance),即一个派生类可以有两个或多个基类。 多继承容易让代码逻辑复杂、思路混乱,一直备受争议,中小型项目中较少使用,后来的 Java、C#、PHP 等干脆取消了多继承。 …...
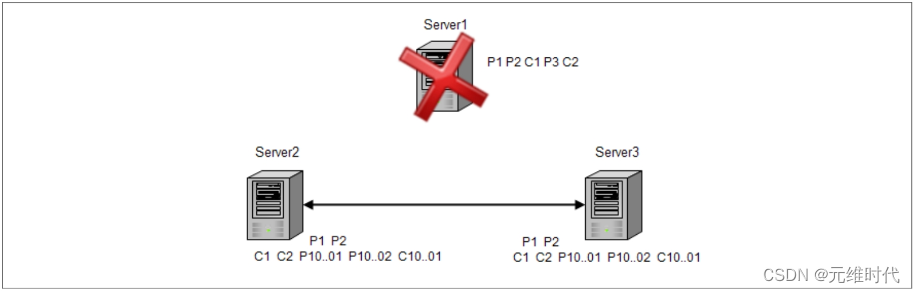
ZooKeeper与Paxos
Apache ZooKeeper是由Apache Hadoop的子项目发展而来,于2010年11月正式成为了Apache的顶级项目。ZooKeeper为分布式应用提供了高效且可靠的分布式协调服务,提供了诸如统一命名服务、配置管理和分布式锁等分布式的基础服务。在解决分布式数据一致性方面&a…...

Cargo 静态编译
git clone --recursive https://github.com/kornelski/pngquant.git vi ~/.cargo/config.toml[http] debug true proxy "127.0.0.1:1080" 1.apt 更新 2.apt install cargo 3.修改源码的Cargo.toml [source.crates-io] #registry "https://code.aliyun.com…...

【多线程】有两个线程都能访问n,初始时n为0,⼀个线程执⾏n++,n+=2,另⼀个线程执⾏n+=3,当两个线程都执行完后n可能的值
必备知识点:n 在底层是由三条指令在CPU完成的 load : 将内存的值读取到CPU寄存器add : 将CPU寄存器中的值进行1操作save : 将CPU寄存器中的值写回内容 回答 首先n操作在底层是由三条指令在CPU完成的,先要将内存中n的值读取到CPU寄存器,然后…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...
