滑动窗口系列1-达标子数组
#达标子数组#
求达标子数组的数量 * 题目:给定一个数组,求满足子数组中最大值-最小值小于等于某个数的子数组的数量 * 例如[0,1,2,3]中求子数组中最大值-最小值小于等于 2的子数组的数量 * 结果为9,因为满足条件的只有[0,0] [0,1] [0,2] [1,1] [1,2] [1,3] [2,2] [2,3] [3,3]
题目对应的代码如下:
首先讨论暴力解,这种解法特别容易想,就是把所有的子数组进行枚举,例如:0~0,0~1,0~2,0~3, 0~4...2~2,2~2,2~3,2~4...然后依次找到每个子数组的最大值和最小值,根据二者之差判断是否达标,如果达标则总的数量加1,两层for循环的时间复杂度是O(N^2),面试场没分
重点讨论第二种解法,也是本题的重要考察点:滑动窗口,对于滑动窗口解法来说,每个位置最多进一次窗口,也最多出一次窗口,所以时间复杂度是O(N),这个已经是最好的解法了,你不可能所有的位置都没看完就找到所有答案
public class AllLessNumSubArray {/*** 暴力解,百分百正确,但是面试场上没分*/public static int right(int[] nums, int limit) {if(nums == null || nums.length == 0 || limit < 0) {return 0;}int result = 0;for(int i = 0; i < nums.length; i++) {int max = nums[i];int min = nums[i];for(int j = i; j < nums.length; j++) {max = Math.max(max, nums[j]);min = Math.min(min, nums[j]);if(max - min > limit) break;if(max - min <= limit) result ++;}}return result;}public static int better(int[] nums, int limit) {//不满足基本的条件,返回0个if(nums == null || nums.length == 0 || limit < 0) {return 0;}//数组的长度int N = nums.length;//创建最大值和最小值窗口,使用双端队列LinkedList<Integer> min = new LinkedList<>();LinkedList<Integer> max = new LinkedList<>();//L和R都从0开始,形成的区间是[L,R]左开右闭int R = 0;int L = 0;//最终结果统计int result = 0;//L,R的边界都是小于N,都是不回退的while(L < N) {while(R < N) {//如果当前最小值窗口中有数字大于要进去的R的位置的数字,依次弹出while(!min.isEmpty() && nums[min.peekLast()] >= nums[R]) {min.pollLast();}//R入最小值窗口min.addLast(R);//如果当前最大值窗口中有数字小于要进去的R的位置的数字,依次弹出while(!max.isEmpty() && nums[max.peekLast()] <= nums[R]) {max.pollLast();}//R入最小值窗口max.addLast(R);//当前窗口最大值-最小值如果不满足《=limit,终止,//如果满足条件R继续++,R是以L下标开始第一个不满足条件的if(nums[max.peekFirst()] - nums[min.peekFirst()] > limit) {break;} else {R++;}}//因为L马上要进行L++操作了,所以L位置马上过期,如果最大值或者最小值窗口的头部是L,则弹出头部if(max.peekFirst() == L) {max.pollFirst();}if(min.peekFirst() == L) {min.pollFirst();}//R是以L为起点的子数组中第一个不满足max-min<=limit的节点,所以数量加上(R - L)result += (R - L);L++;}return result;}}相关文章:

滑动窗口系列1-达标子数组
#达标子数组# 求达标子数组的数量 * 题目:给定一个数组,求满足子数组中最大值-最小值小于等于某个数的子数组的数量 * 例如[0,1,2,3]中求子数组中最大值-最小值小于等于 2的子数组的数量 * 结果为9,因为满足条件的只有[0,0] [0,1] [0,2] [1,1] [1,2] [1…...
)
电视显示技术及价格成本对比(2023年)
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。 本文链接:https://blog.csdn.net/zaibeijixing/article/details/132461068 ———————————————— 截止到2023年ÿ…...

浅谈 Pytest+HttpRunner 如何展开接口测试!
软件测试有多种多样的方法和技术,可以从不同角度对它们进行分类。其中,根据软件生命周期,针对不同的测试对象与目标,可将测试过程分为 4 个阶段:单元测试、集成测试、系统测试和验收测试。本文着重介绍了如何借用 pyte…...
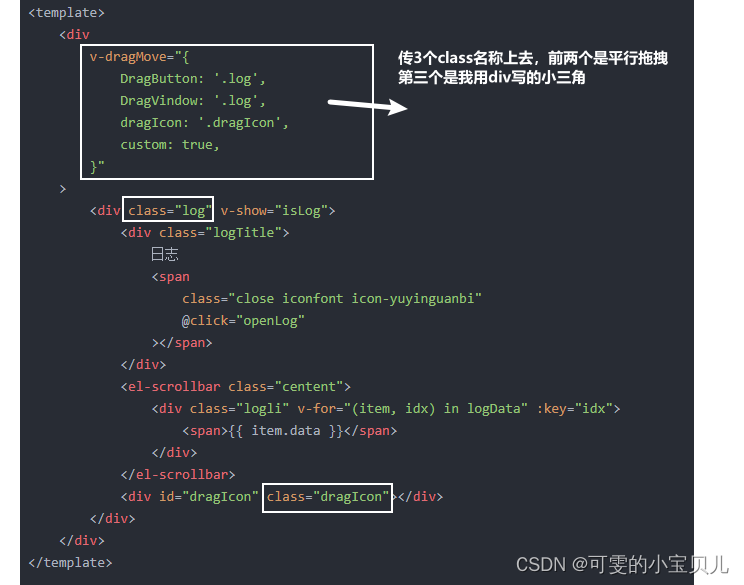
vue自定义事件 div 拖拽方法缩小
在main.js 引用 // 引入拖动js import dragMove from "./utils/dragMove.js" 创建 drawmove.js export default (app) > {app.directive(dragMove, (el, binding) > {const DragVindow el.querySelector(binding.value.DragVindow)// 按下鼠标处理事件con…...

使用实体解析和图形神经网络进行欺诈检测
图形神经网络的表示形式(作者使用必应图像创建器生成的图像) 一、说明 对于金融、电子商务和其他相关行业来说,在线欺诈是一个日益严重的问题。为了应对这种威胁,组织使用基于机器学习和行为分析的欺诈检测机制。这些技术能够实时…...

vue中axios请求篇
vue中如何发起请求? 利用axios来发起请求,但是前期需要配置 首先安装axios 可以使用npm、yarn等进行安装 npm安装方式 npm install axios -sava //在项目文件夹中打开cmd或者终端进行安装依赖 yarn安装方式 yarn add axios 引入axios。我一般是在src下创建一个u…...
Springboot2.0 上传图片 jar包导出启动(第二章)
目录 一,目录文件结构讲解二,文件上传实战三,jar包方式运行web项目的文件上传和访问处理(核心知识)最后 一,目录文件结构讲解 简介:讲解SpringBoot目录文件结构和官方推荐的目录规范 1、目录讲解…...
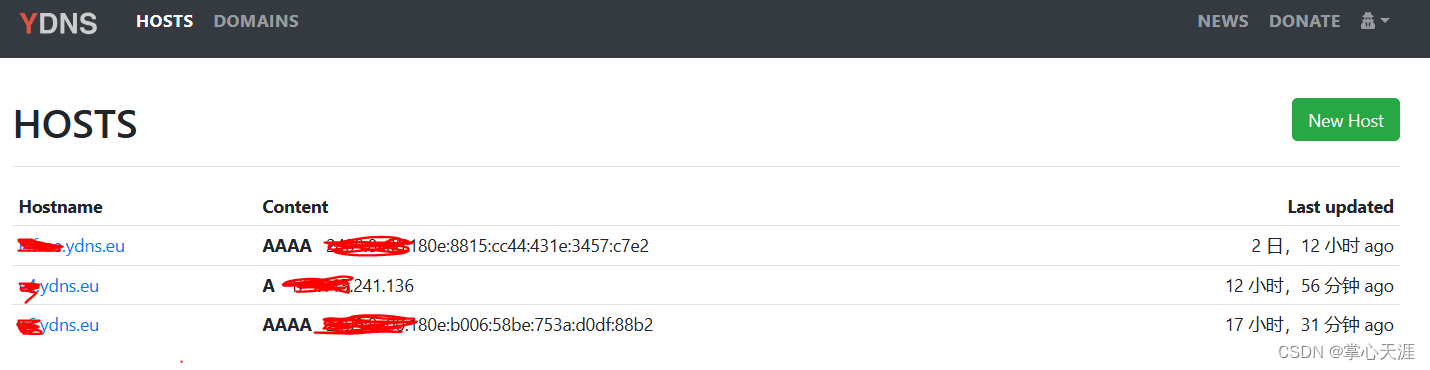
添加YDNS免费的ipv6动态域名解析
背景 又到了一年一度的dns域名到期,寻找替代了,前几年用了阿里、华为的免费域名,支持了几个搭建在NAS上的微服务;一旦涉及到域名续费,价格就比首年上去了不少,所以,打算找个长期的免费域名。 搜…...

爬虫异常处理之如何处理连接丢失和数据存储异常
在爬虫开发过程中,我们可能会遇到各种异常情况,如连接丢失、数据存储异常等。本文将介绍如何处理这些异常,并提供具体的解决代码。我们将以Python语言为例,使用requests库进行网络请求和sqlite3库进行数据存储。 1. 处理连接丢失 …...
KVM虚拟化ubuntu
KVM(Kernel-based Virtual Machine)是一种基于Linux内核的虚拟化技术,它将Linux内核作为虚拟机的底层操作系统,利用硬件虚拟化支持创建和管理虚拟机。KVM虚拟化技术被广泛应用于云计算、虚拟化服务器、虚拟化桌面等场景。 KVM虚拟…...
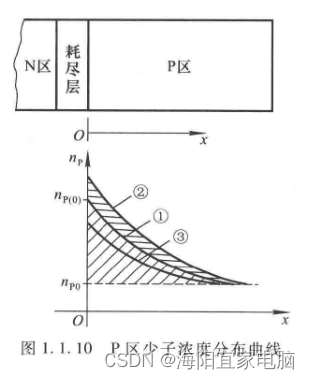
模拟电子技术基础学习笔记三 PN结
采用不周的掺杂工艺,将P型半导体与N型半导体制作在同一块硅片上,在它们的交界面就形成PN结。 扩散运动 物质总是从浓度高的地方向浓度低的地方运动,这种由于浓度差而产生的运动称为扩散运动。 空间电荷区 - 耗尽层 漂移运动 在电场力的作…...

java基础-----第七篇
系列文章目录 文章目录 系列文章目录一、什么是字节码?采用字节码的好处是什么?1.java中的编译器和解释器:2.采用字节码的好处:二、Java中的异常体系一、什么是字节码?采用字节码的好处是什么? 1.java中的编译器和解释器: Java中引入了虚拟机的概念,即在机器和编译程…...
useEffect 不可忽视的 cleanup 函数
在 react 开发中, useEffect 是我们经常会使用到的钩子,一个基础的例子如下: useEffect(() > {// some code here// cleanup 函数return () > {doSomething()} }, [dependencies])上述代码中, cleanup 函数的执行时机有如下…...

vue3:使用:批量删除功能
场景:vue中使用el-table,常需要记住上一页所勾选的数据,批量删除操作,或者弹窗分页勾选,进行第一页勾选,在调后端接口选择第二页勾选其他数据。 1、element-ui 的table表格可以轻松实现多选的功能,只要在表…...

Scala中的样例类和样例对象和JAVA存根类
Scala中的样例类和样例对象 在 Scala 中,样例类(case class)和样例对象(case object)都是用于定义不可变数据类型的特殊类和对象。它们被广泛用于模式匹配、代数数据类型(Algebraic Data Types)…...

【0218】当SIGQUIT kill掉stats collector后,stats collector如何保存最终统计数据
1. stats collector可被哪些信号给kill? stats collector进程的主体函数是 PgstatCollectorMain(),该函数内部完成了stats collector进程的信号注册、现有统计文件读取、消息处理等任务。 忽略通常与postmaster中的某些操作绑定的所有信号,SIGHUP和SIGQUIT除外。 注意,我们…...

httplib 与 json.hpp 结合示例
httplib 与 json.hpp 结合示例 1、使用POST 接口,发送 登陆 请求 客户端发送 {nlohmann::json jsonOfCollectionInfo;jsonOfCollectionInfo["user_id"] "zhang";jsonOfCollectionInfo["password"] "123456";httplib::…...

RK3288安卓7.1开机上电到显示logo需要在3s内完成
需求: 从上电到开始开机logo有一段黑屏时间,这个黑屏时间大概在6s左右,给客户体验很不好,现在需要将这段黑屏时间缩短到2-3s左右 思路: 因为只需要早点显示logo,其实整体从上电到开机动画到安卓系统启动整体…...

Maven之hibernate-validator 高版本问题
hibernate-validator 高版本问题 hibernate-validator 的高版本(邮箱注解)依赖于高版本的 el-api,tomcat 8 的 el-api 是 3.0,满足需要。但是 tomcat 7 的 el-api 只有 2.2,不满足其要求。 解决办法有 2 种ÿ…...
C++--动态规划其他问题
1.一和零 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 给你一个二进制字符串数组 strs 和两个整数 m 和 n 。 请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。 如果 x 的所有元素也是 y 的元素࿰…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...
