LeetCode 23 合并 K 个升序链表
LeetCode 23 合并 K 个升序链表
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/merge-k-sorted-lists/description/
博主Github:https://github.com/GDUT-Rp/LeetCode
题目:
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例1:
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[1->4->5,1->3->4,2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
示例2:
输入:lists = []
输出:[]
示例3:
输入:lists = [[]]
输出:[]
提示:
- k == lists.length
- 0 <= k <= 1 0 4 10^4 104
- 0 <= lists[i].length <= 500
- − 1 0 4 -10^4 −104 <= lists[i][j] <= 1 0 4 10^4 104
- lists[i] 按 升序 排列
- lists[i].length 的总和不超过 10^4
解题思路:
方法一:顺序合并
用一个变量 ans 来维护以及合并的链表,第 i 次循环把第 i 个链表和 ans 合并,答案保存到 ans 中。
Golang
/*** Definition for singly-linked list.* type ListNode struct {* Val int* Next *ListNode* }*/
func mergeKLists(lists []*ListNode) *ListNode {var ans *ListNodefor i:=0; i<len(lists); i++ {ans = mergeTwoLists(ans, lists[i])}return ans
}func mergeTwoLists(a *ListNode, b *ListNode) *ListNode {if a == nil {return b}if b == nil {return a}var head ListNodetail := &headfor (a != nil && b != nil) {if a.Val < b.Val {tail.Next = aa = a.Next} else {tail.Next = bb = b.Next}tail = tail.Next}if a != nil {tail.Next = a} else {tail.Next = b}return head.Next
}
C++
class Solution {
public:ListNode* mergeTwoLists(ListNode *a, ListNode *b) {if ((!a) || (!b)) return a ? a : b;ListNode head, *tail = &head, *aPtr = a, *bPtr = b;while (aPtr && bPtr) {if (aPtr->val < bPtr->val) {tail->next = aPtr; aPtr = aPtr->next;} else {tail->next = bPtr; bPtr = bPtr->next;}tail = tail->next;}tail->next = (aPtr ? aPtr : bPtr);return head.next;}ListNode* mergeKLists(vector<ListNode*>& lists) {ListNode *ans = nullptr;for (size_t i = 0; i < lists.size(); ++i) {ans = mergeTwoLists(ans, lists[i]);}return ans;}
};
Java
class Solution {public ListNode mergeKLists(ListNode[] lists) {ListNode ans = null;for (int i = 0; i < lists.length; ++i) {ans = mergeTwoLists(ans, lists[i]);}return ans;}public ListNode mergeTwoLists(ListNode a, ListNode b) {if (a == null || b == null) {return a != null ? a : b;}ListNode head = new ListNode(0);ListNode tail = head, aPtr = a, bPtr = b;while (aPtr != null && bPtr != null) {if (aPtr.val < bPtr.val) {tail.next = aPtr;aPtr = aPtr.next;} else {tail.next = bPtr;bPtr = bPtr.next;}tail = tail.next;}tail.next = (aPtr != null ? aPtr : bPtr);return head.next;}
}
复杂度分析
时间复杂度: 假设每个链表的最长长度是 n。在第一次合并后,ans 的长度为 n;第二次合并后,ans 的长度为 2n,第 i 次合并后,ans 的长度为 i×n。第 i 次合并的时间代价是 O(n+(i−1)×n)=O(i×n),那么总的时间代价为 O ( ∑ i = 1 k ( i × n ) ) = O ( ( 1 + k ) ⋅ k 2 × n ) = O ( k 2 n ) O(\sum_{i = 1}^{k} (i \times n)) = O(\frac{(1 + k)\cdot k}{2} \times n) = O(k^2 n) O(∑i=1k(i×n))=O(2(1+k)⋅k×n)=O(k2n),故渐进时间复杂度为 O ( k 2 n ) O(k^2 n) O(k2n)。
空间复杂度 O(1) 。
方法二:分治合并
考虑优化方法一,用分治的方法进行合并。
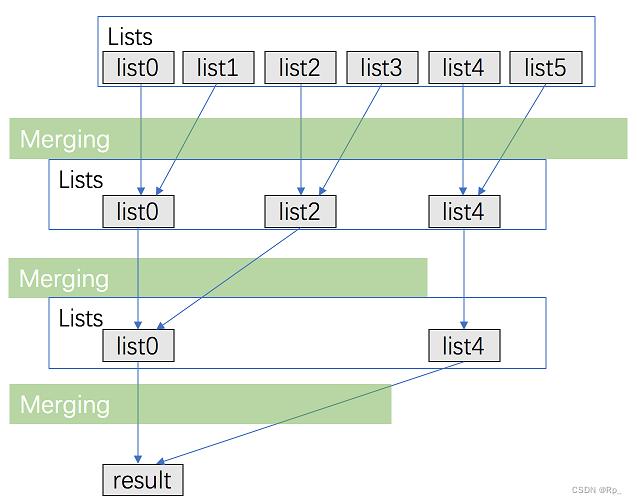
- 将 kkk 个链表配对并将同一对中的链表合并;
- 第一轮合并以后, k 个链表被合并成了 k 2 \frac{k}{2} 2k 个链表,平均长度为 2 n k \frac{2n}{k} k2n,然后是 k 4 \frac{k}{4} 4k 个链表, k 8 \frac{k}{8} 8k 个链表等等;
- 重复这一过程,直到我们得到了最终的有序链表。
Golang
/*** Definition for singly-linked list.* type ListNode struct {* Val int* Next *ListNode* }*/
func mergeKLists(lists []*ListNode) *ListNode {return merge(lists, 0, len(lists) - 1)
}func merge(lists []*ListNode, left, right int) *ListNode {if left == right {return lists[left]}if left > right {return nil}mid := (left + right) >> 1return mergeTwoLists(merge(lists, left, mid), merge(lists, mid+1, right))
}func mergeTwoLists(a *ListNode, b *ListNode) *ListNode {if a == nil {return b}if b == nil {return a}var head ListNodetail := &headfor (a != nil && b != nil) {if a.Val < b.Val {tail.Next = aa = a.Next} else {tail.Next = bb = b.Next}tail = tail.Next}if a != nil {tail.Next = a} else {tail.Next = b}return head.Next
}
C++
class Solution {
public:ListNode* mergeTwoLists(ListNode *a, ListNode *b) {if ((!a) || (!b)) return a ? a : b;ListNode head, *tail = &head, *aPtr = a, *bPtr = b;while (aPtr && bPtr) {if (aPtr->val < bPtr->val) {tail->next = aPtr; aPtr = aPtr->next;} else {tail->next = bPtr; bPtr = bPtr->next;}tail = tail->next;}tail->next = (aPtr ? aPtr : bPtr);return head.next;}ListNode* merge(vector <ListNode*> &lists, int l, int r) {if (l == r) return lists[l];if (l > r) return nullptr;int mid = (l + r) >> 1;return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));}ListNode* mergeKLists(vector<ListNode*>& lists) {return merge(lists, 0, lists.size() - 1);}
};
Java
class Solution {public ListNode mergeKLists(ListNode[] lists) {return merge(lists, 0, lists.length - 1);}public ListNode merge(ListNode[] lists, int l, int r) {if (l == r) {return lists[l];}if (l > r) {return null;}int mid = (l + r) >> 1;return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));}public ListNode mergeTwoLists(ListNode a, ListNode b) {if (a == null || b == null) {return a != null ? a : b;}ListNode head = new ListNode(0);ListNode tail = head, aPtr = a, bPtr = b;while (aPtr != null && bPtr != null) {if (aPtr.val < bPtr.val) {tail.next = aPtr;aPtr = aPtr.next;} else {tail.next = bPtr;bPtr = bPtr.next;}tail = tail.next;}tail.next = (aPtr != null ? aPtr : bPtr);return head.next;}
}
时间复杂度:考虑递归「向上回升」的过程——第一轮合并 k 2 \frac{k}{2} 2k 组链表,每一组的时间代价是 O ( 2 n ) O(2n) O(2n);第二轮合并 k 4 \frac{k}{4} 4k 组链表,每一组的时间代价是 O ( 4 n ) O(4n) O(4n)…所以总的时间代价是 O ( ∑ i = 1 ∞ k 2 i × 2 i n ) = O ( k n × log k ) O(\sum_{i = 1}^{\infty} \frac{k}{2^i} \times 2^i n) = O(kn \times \log k) O(∑i=1∞2ik×2in)=O(kn×logk),故渐进时间复杂度为 O ( k n × log k ) O(kn \times \log k) O(kn×logk)
空间复杂度:递归会使用到 O ( log k ) O(\log k) O(logk) 空间代价的栈空间。
方法三:使用优先队列/最小堆合并
这个方法和前两种方法的思路有所不同
我们需要维护当前每个链表没有被合并的元素的最前面一个, k k k 个链表就最多有 k k k 个满足这样条件的元素,每次在这些元素里面选取 val 属性最小的元素合并到答案中。
在选取最小元素的时候,我们可以用优先队列/最小堆来优化这个过程。
Golang
/*** Definition for singly-linked list.* type ListNode struct {* Val int* Next *ListNode* }*/import "container/heap"type Status struct {Val intPtr *ListNode
}type PriorityQueue []*Statusfunc (pq PriorityQueue) Len() int {return len(pq)
}func (pq PriorityQueue) Less(i, j int) bool {return pq[i].Val < pq[j].Val
}func (pq PriorityQueue) Swap(i, j int) {pq[i], pq[j] = pq[j], pq[i]
}func (pq *PriorityQueue) Push(x interface{}) {*pq = append(*pq, x.(*Status))
}func (pq *PriorityQueue) Pop() interface{} {old := *pqn := len(old)item := old[n-1]old[n-1] = nil*pq = old[0 : n-1]return item
}func mergeKLists(lists []*ListNode) *ListNode {var q PriorityQueueheap.Init(&q)for _, node := range lists {// 每个链表第一个都放进这个堆if node != nil {heap.Push(&q, &Status{Val: node.Val, Ptr: node})}}var head ListNodetail := &headfor q.Len() > 0 {// 取出最小的f := heap.Pop(&q).(*Status)tail.Next = f.Ptrtail = tail.Next// 只要所取的节点后面还要数据if f.Ptr.Next != nil {// 就放进堆里来heap.Push(&q, &Status{Val: f.Ptr.Next.Val, Ptr: f.Ptr.Next})}}return head.Next
}
Java
class Solution {class Status implements Comparable<Status> {int val;ListNode ptr;Status(int val, ListNode ptr) {this.val = val;this.ptr = ptr;}public int compareTo(Status status2) {return this.val - status2.val;}}PriorityQueue<Status> queue = new PriorityQueue<Status>();public ListNode mergeKLists(ListNode[] lists) {for (ListNode node: lists) {if (node != null) {queue.offer(new Status(node.val, node));}}ListNode head = new ListNode(0);ListNode tail = head;while (!queue.isEmpty()) {Status f = queue.poll();tail.next = f.ptr;tail = tail.next;if (f.ptr.next != null) {queue.offer(new Status(f.ptr.next.val, f.ptr.next));}}return head.next;}
}
C++
class Solution {
public:struct Status {int val;ListNode *ptr;bool operator < (const Status &rhs) const {return val > rhs.val;}};priority_queue <Status> q;ListNode* mergeKLists(vector<ListNode*>& lists) {for (auto node: lists) {if (node) q.push({node->val, node});}ListNode head, *tail = &head;while (!q.empty()) {auto f = q.top(); q.pop();tail->next = f.ptr; tail = tail->next;if (f.ptr->next) q.push({f.ptr->next->val, f.ptr->next});}return head.next;}
};
复杂度分析
时间复杂度:考虑优先队列中的元素不超过 k k k 个,那么插入和删除的时间代价为 ¥O(\log k)$,这里最多有 k n kn kn 个点,对于每个点都被插入删除各一次,故总的时间代价即渐进时间复杂度为 O ( k n × log k ) O(kn \times \log k) O(kn×logk)。
空间复杂度:这里用了优先队列,优先队列中的元素不超过 k k k 个,故渐进空间复杂度为 O ( k ) O(k) O(k)。
相关文章:

LeetCode 23 合并 K 个升序链表
LeetCode 23 合并 K 个升序链表 来源:力扣(LeetCode) 链接:https://leetcode.cn/problems/merge-k-sorted-lists/description/ 博主Github:https://github.com/GDUT-Rp/LeetCode 题目: 给你一个链表数组…...

[国产MCU]-W801开发实例-TCP客户端
TCP客户端 文章目录 TCP客户端1、TCP协议简单介绍2、W801创建TCP客户流程本文将详细介绍如何在W801中使用TCP客户端。 1、TCP协议简单介绍 传输控制协议 (TCP) 是一种标准,它定义了如何建立和维护应用程序可以用来交换数据的网络对话。 TCP 与 Internet 协议 (IP) 一起工作,…...
《爵士乐史》乔德.泰亚 笔记
第一章 【美国音乐的非洲化】 【乡村布鲁斯和经典布鲁斯】 布鲁斯:不止包括忧愁、哀痛 十二小节布鲁斯特征: 1.乐型(A:主、B:属、C/D:下属):A→A→B→A→C→D→A→A 2.旋律:大三、小三、降七、降五 盲人…...

工程制造领域:企业IT架构
一、IT组织规划架构图 1.1 IT服务保证梯队与指导思想 二、整体业务规划架构图 三、数据化项目规划架构图 四、应用系统集成架构图...

PY32F003F18点灯
延时函数学习完之后,可以学习PY32F003F18的GPIO输出功能。 1、Debug引脚默认被置于复用功能上拉或下拉模式:PA14默认为SWCLK: 置于下拉模式PA13默认为SWDIO: 置于上拉模式PF4默认为Boot:Boot引脚默认置于输入下拉模式 2、GPIO输出状态&#…...
Mac不想用iTerm2了怎么办
这东西真是让人又爱又恨,爱的是它的UI还真不错,恨的是它把我的环境给破坏啦!让我每次启动终端之后都要重新source激活我的python环境,而且虚拟环境前面没有括号啦!这怎么能忍!在UI和实用性面前我断然选择实…...

x86_64 ansible 源码编译安装
源码 GitHub - ansible/ansible: Ansible is a radically simple IT automation platform that makes your applications and systems easier to deploy and maintain. Automate everything from code deployment to network configuration to cloud management, in a languag…...

数据结构学习系列之顺序表的两种插入方式
方式1:在顺序表末端插入数据元素,代码如下:示例代码: int insert_seq_list_1(list_t *seq_list,int data){if(NULL seq_list){printf("入参为NULL\n");return -1;}if(N seq_list->count){printf("顺序表已满…...
)
Matlab/Python教程系列 | 根据目录下的已有图片制作视频(动画)
MATLAB和Python的编程教程: 根据目录下的已有图片制作视频(动画) 注1:本文系“MATLAB/Python编程教程”系列之一,致力于使用Python和Matlab实现特定的功能。本次要实现的功能是:根据目录下的已有图片制作视频(动画)。 在这个教程中,我们将一起学习如何使用MATLAB和Python编…...
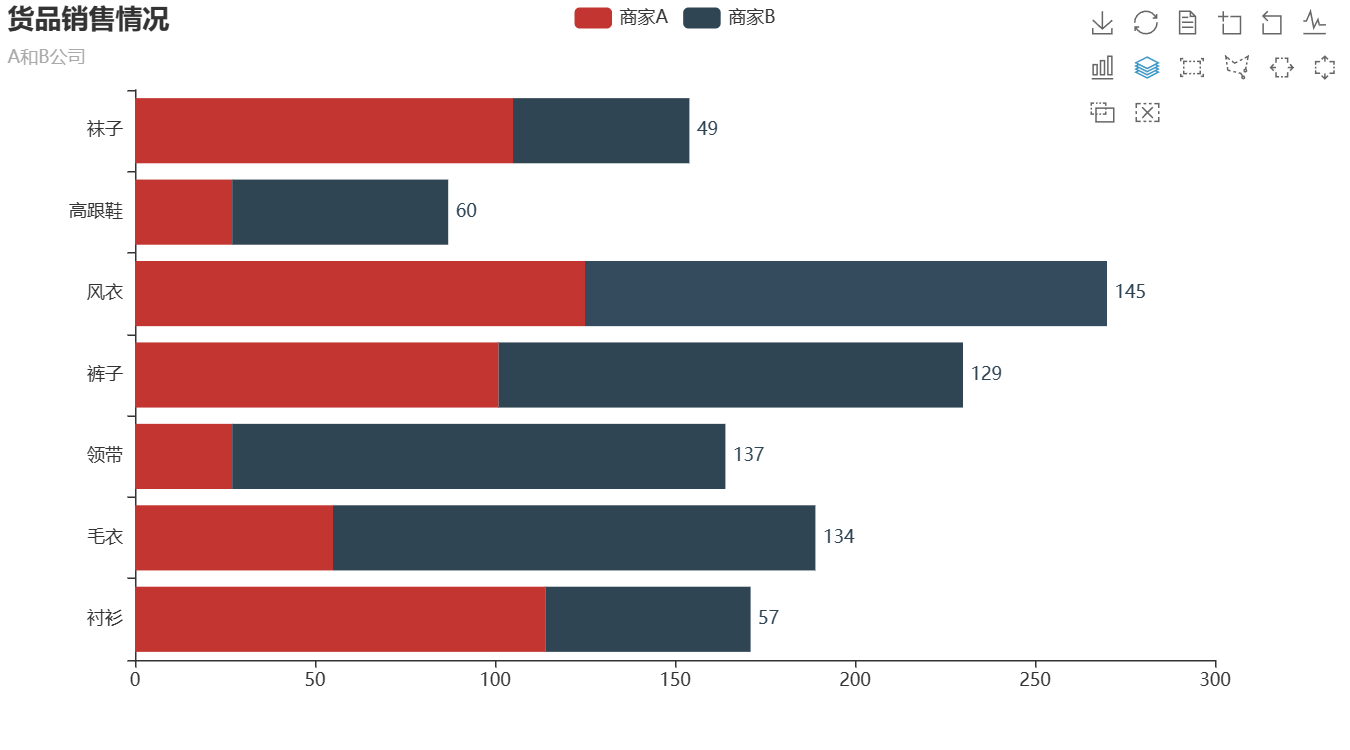
Pyecharts数据可视化(一)
目录 1.Pyecharts简介 2.Pyecharts的常用方法 3.Pyecharts绘制柱状图 3.1 绘制并列柱状图 3.2 绘制水平直方图 1.Pyecharts简介 Pyecharts是一个用于创建交互式图表的Python库。它基于Echarts,一个强大的JavaScript图表库,Pyecharts允许Python开发者…...

stable diffusion实践操作-提示词-图片结构
系列文章目录 stable diffusion实践操作-提示词 文章目录 系列文章目录前言一、提示词汇总1.1 图片结构11.2 图片结构21.3 图片结构3 二、总结 前言 本文主要收纳总结了提示词-图片结构。 一、提示词汇总 1.1 图片结构1 StylesArtistshudson river school哈得逊河学派alpho…...

程序员自由创业周记#2:前期准备
感恩 上次公开了创业的决定后,得到了很多亲朋好友和陌生朋友的鼓励或支持,以不同的形式,感动之情溢于言表。这些都会记在心里,大恩不言谢~ 创业方向 笔者是一名资质平平的iOS开发程序猿,创业项目也就是开发App卖&am…...
:Springboot实现Elasticsearch指标聚合与下钻分析open-API)
Elasticsearch实战(四):Springboot实现Elasticsearch指标聚合与下钻分析open-API
文章目录 系列文章索引一、指标聚合与分类1、什么是指标聚合(Metric)2、Metric聚合分析分为单值分析和多值分析两类3、概述 二、单值分析API设计1、Avg(平均值)(1)对所有文档进行avg聚合(DSL)(2…...
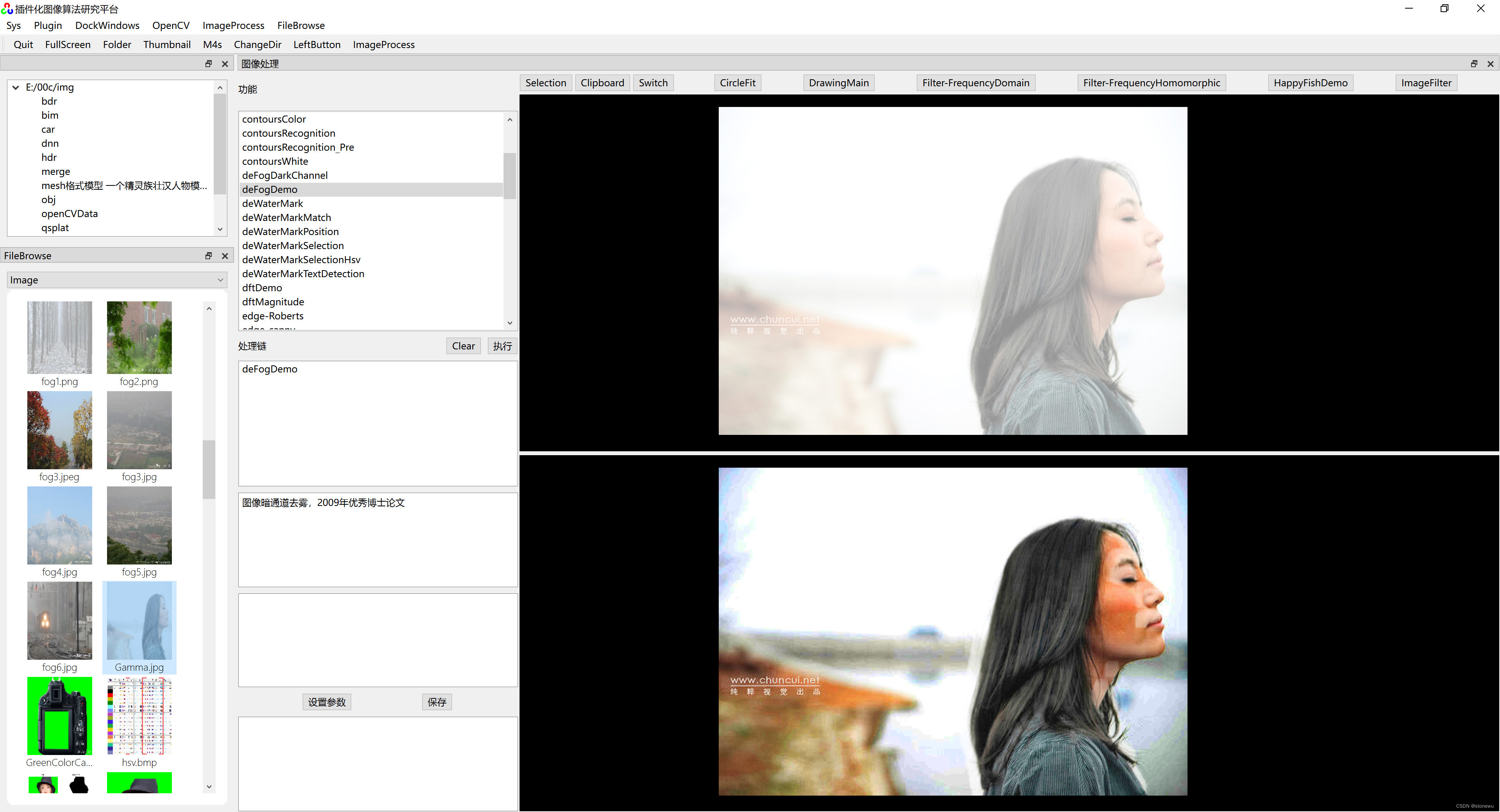
Opencv图像暗通道调优
基于雾天退化模型的去雾算法,Opencv图像暗通道调优,(清华版代码)对普通相片也有较好的调优效果,相片更通透。 结合代码实际运行效果、算法理论模型、实际代码。我个人理解,实际效果是对图像的三个颜色通道…...

怎样来实现流量削峰方案
削峰从本质上来说就是更多地延缓用户请求,以及层层过滤用户的访问需求,遵从“最后落地到数据库的请求数要尽量少”的原则。 1.消息队列解决削峰 要对流量进行削峰,最容易想到的解决方案就是用消息队列来缓冲瞬时流量,把同步的直…...

git status搜索.c和.h后缀及git新建分支
git status搜索.c和.h后缀及git新建分支 1.脚本代码2.git新建分支(1)创建新分支(2)删除本地分支(3)删除远端分支(4)合并分支3.指定历史版本创建分支1.脚本代码 $ git status | grep "\.[hc]$"$ 是行尾的意思 \b 就是用在你匹配整个单词的时候。 如果不是整个…...

【配置环境】Visual Studio 配置 OpenCV
目录 一,环境 二,下载和配置 OpenCV 三,创建一个 Visual Studio 项目 四,配置 Visual Studio 项目 五,编写并编译 OpenCV 程序 六,解决CMake编译OpenCV报的错误 一,环境 Windows 11 家庭中…...
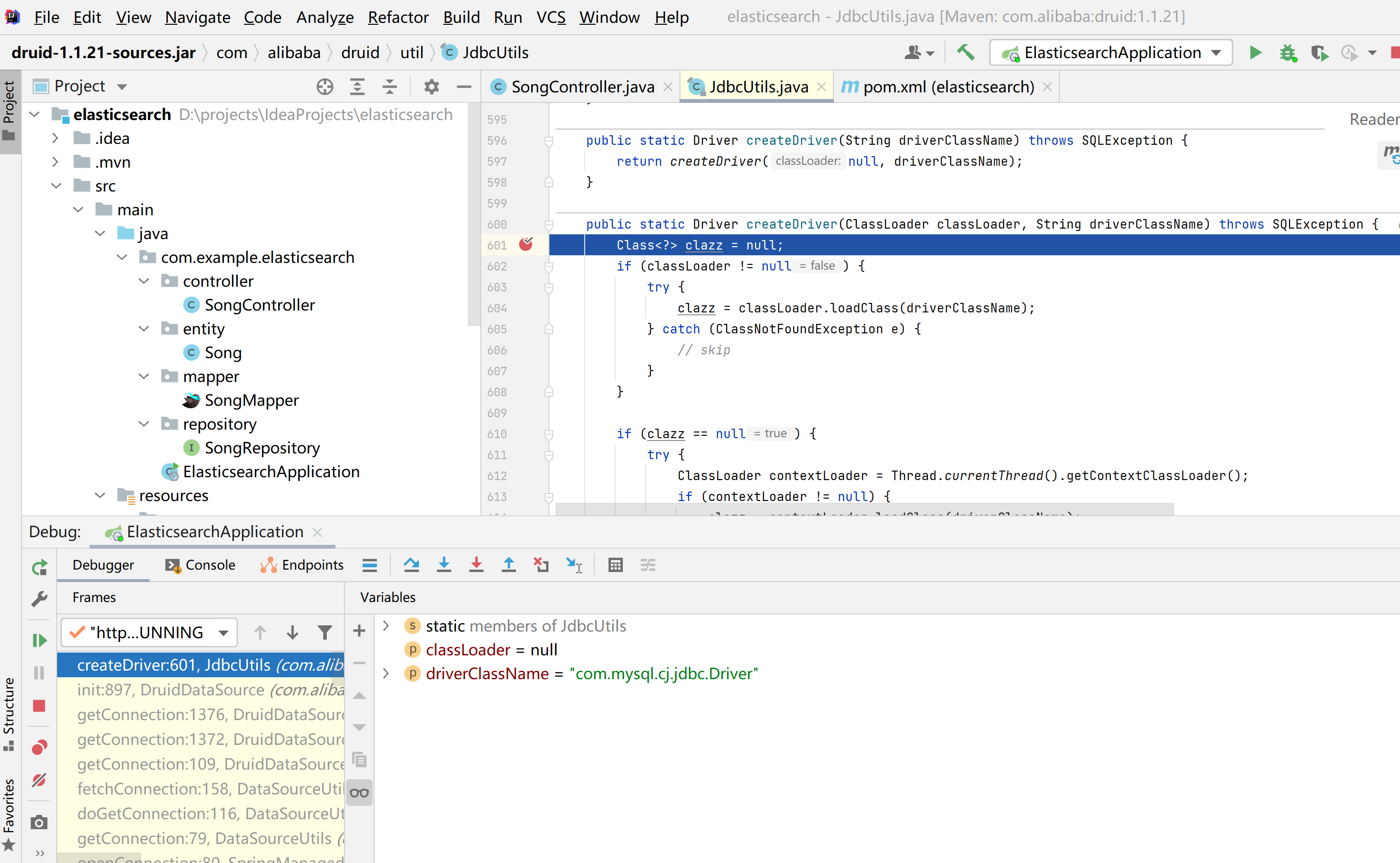
java.sql.SQLException: com.mysql.cj.jdbc.Driver
这篇文章分享一下Springboot整合Elasticsearch时遇到的一个问题,项目正常启动,但是查询数据库的时候发生了一个异常java.sql.SQLException: com.mysql.cj.jdbc.Driver java.sql.SQLException: com.mysql.cj.jdbc.Driverat com.alibaba.druid.util.JdbcU…...
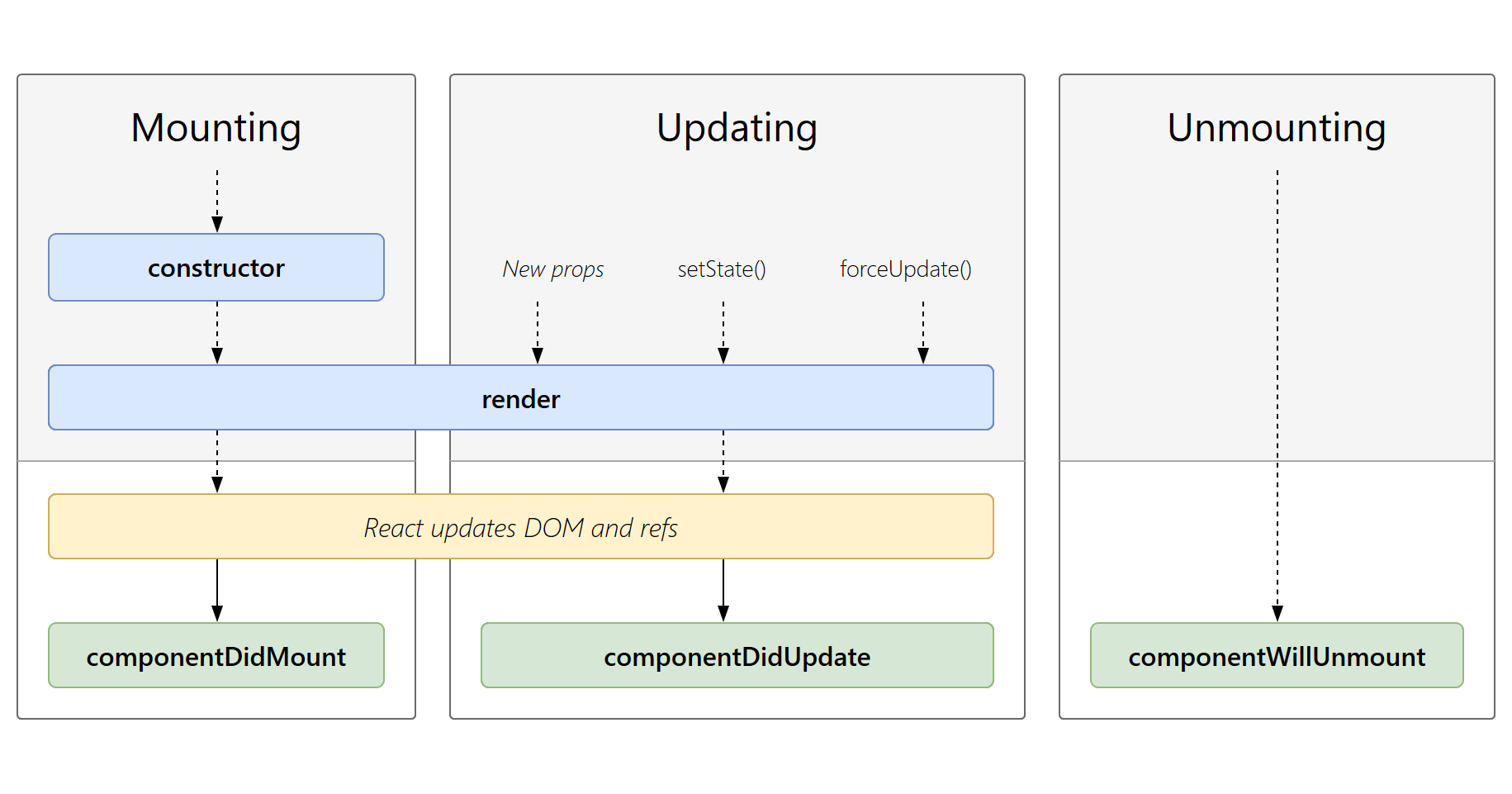
React笔记(四)类组件(2)
一、类组件的props属性 组件中的数据,除了组件内部的状态使用state之外,状态也可以来自组件的外部,外部的状态使用类组件实例上另外一个属性来表示props 1、基本的使用 在components下创建UserInfo组件 import React, { Component } from…...

点云从入门到精通技术详解100篇-点云信息编码
目录 前言 研究发展现状 点云几何信息压缩 点云属性信息压缩 点云压缩算法的相关技术...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...
