JS算法与树(二)
前言
二叉搜索树(BST)存在一个问题:当你添加的节点数够多的时候,树的一边可能会非常的深。而其他的分支却只有几层。

AVL树
为了解决上面的问题,我们提出一种自平衡二叉搜索树。意思是任何一个节点左右两侧子树的高度之差最多为1。
添加或移除节点时,AVL树会尝试自动保持自平衡,任意一个节点(无论深度)的左右子树高度最多相差1。添加或移除节点时。AVL树会尽可能尝试转换为完全数。
节点的高度
节点的高度是从节点到其任意子节点的边的最大值。

那么我们怎么计算某个节点的高度呢?
因为我们并无法事先知道树的哪一层里的左分支深还是右分支深。所以我们需要进行层层比较,层层返回其左右分支深度的最大值。
getNodeHeight(node) {if (node == null) {return -1;}return Math.max(this.getNodeHeight(node.left), this.getNodeHeight(node.right)) + 1;
}递归:
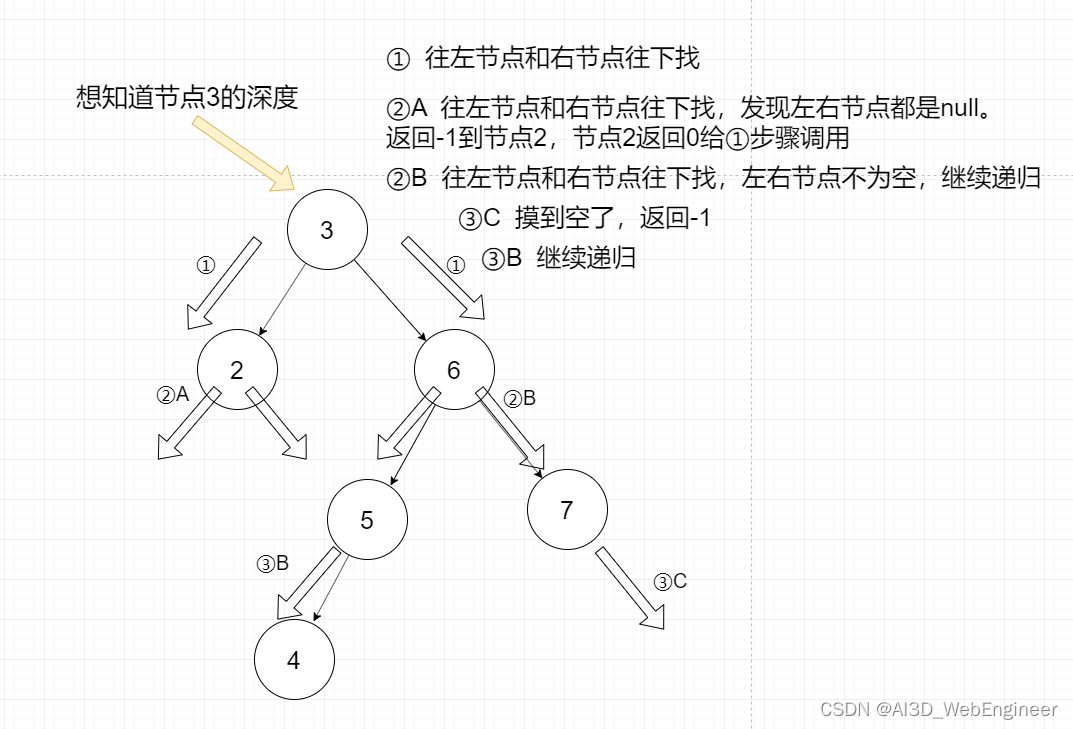
递归后的调用:
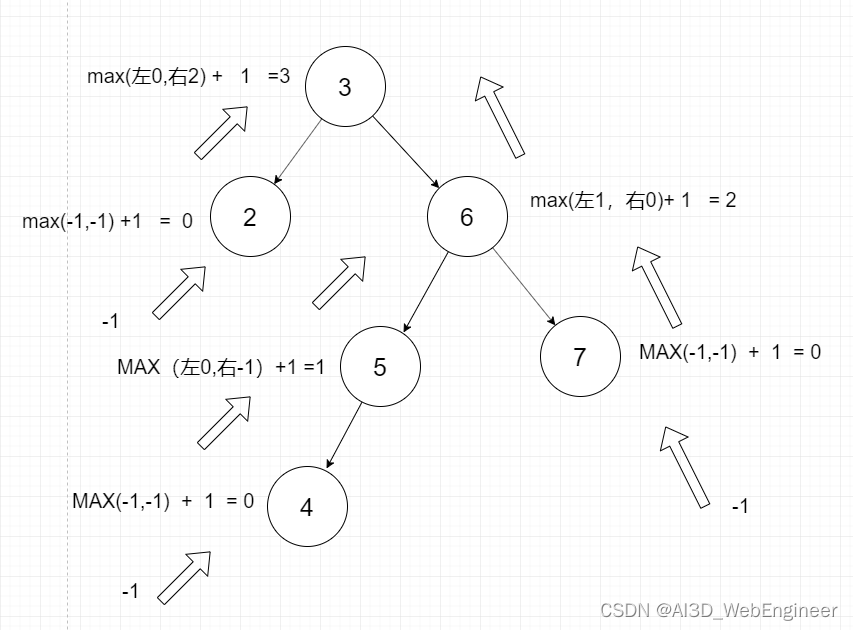
平衡因子
一段能平衡树节点的逻辑。在AVL数中,需要对每个节点计算左子树高度(hl)和右子树高度(hr)。并取其差值。如果差值hr - hl或者hl-hr不为0(一样深),1或-1(只差1个深度)。则需要平衡该AVL树。这就是平衡因子的概念。
我们一般以hr-hl作为平衡因子。

可以看到,我们刚才的例子,并不是一颗平衡树。因为节点3的平衡因子为2。也就是节点3的左子树和右子树不平衡。
计算某个节点的左右子树高度差应该很简单了
getBalanceFactor(node) {const heightDifference = this.getNodeHeight(node.left) - this.getNodeHeight(node.right);
}当高度差大于1的时候,我们就需要对数进行自平衡了。
树的旋转
叉树中任意节点的左右子树的高度差都不大于1。当插入或删除一个节点时,我们需要通过一次或多次树的「旋转」来保持二叉树的平衡。
树的旋转分为「左旋」和「右旋」两种具体操作,这两种操作是完全相反的,互为逆操作。
左旋是「将该节点的右子树逆时针旋转」,右旋是「将该节点的左子树顺时针旋转」。
对于一个节点node进行左旋操作时,具体操作为:「将node.right子树取下,node.right节点称为新的根节点newRoot,将node接在newRoot的左节点,newRoot.left取下接在node的右节点上。」
右旋操作相反:「将node.left子树取下,node.left节点作为新的根节点newRoot,将node接在newRoot的右节点,newRoot.right取下接在node的左节点上。」
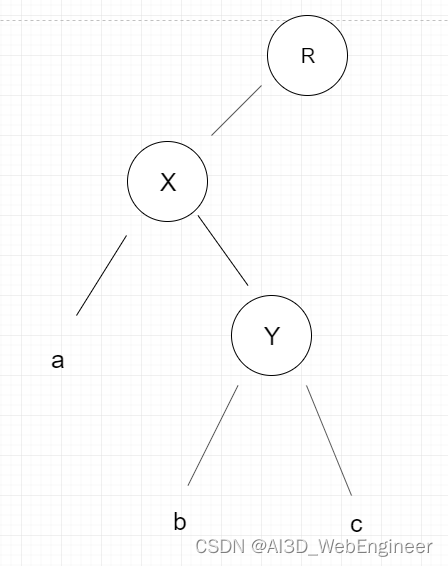
先看这个树,已知的大小关系存在:R>c > Y> b >X >a

右旋RR:【子节点左边多右边少,向右单旋转】 适用于左侧子节点的高度大于右侧子节点的高度,且左侧子节点也是平衡或左侧较重。
左旋LL:【子节点右边多左边少,向左单旋转。适用于左侧节点高度小于右侧子节点高度,且右侧子节点也是平衡或右侧较重
看到这里你可能会觉得疑惑,什么叫平衡或较重?不急,后面自然会解释。

简而言之左旋就是把右树节点放自己头上。右旋就是把左树节点放自己头上
左旋后右旋,便回到最原本的树结构。

左旋代码:RR
rotationRR(node) {// node对应的是X X包含了左右树节点,修改后返回出去// 拿出右节点Yconst tmp = node.right;// 把Y的左节点b拿出来放到X,即node的右节点node.right = tmp.left;// 把X放到Y的左树tmp.left = node;// 返回Yreturn tmp;}右旋代码:LL
rotationLL(node) {const tmp = node.left;node.left = tmp.right;tmp.right = node;return tmp;}这样就结束了吗?当然不是。上面的旋转只是向左向右的单旋转。
AVL不平衡存在四种情况:
第一种情况:R节点的左侧子节点高度高于右侧节点。且R节点的左侧子节点a的子节点(Y-b)重于a的右侧子节点(无)。此时就可以使用我们上面的右旋做法。
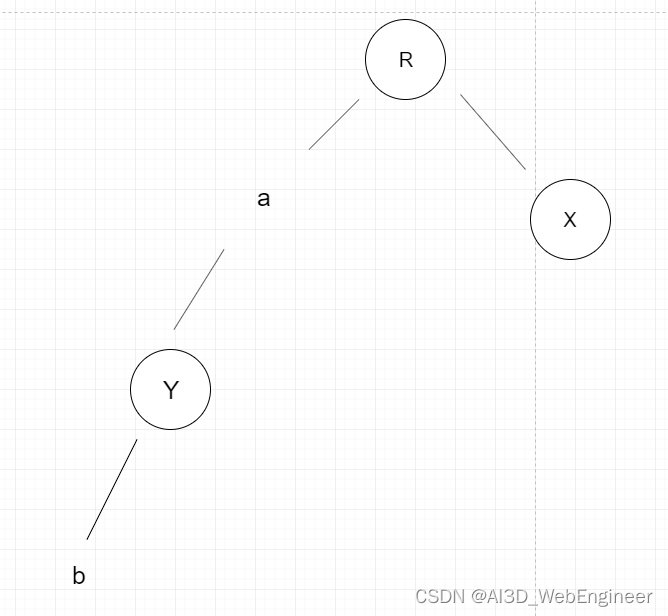
右旋得到:

第二种情况:R节点的右侧子节点高度高于左侧节点。且R节点的右侧子节点a的子节点(Y-b)重于a的左侧子节点(无)。此时就可以使用我们上面的左旋做法。

左旋得到:

第三种情况:R节点的左侧子节点高度高于右侧节点。且R节点的左侧子节点a的子节点(Y-b)重于a的右侧子节点(无)。

如果此时直接右旋:

依然不平衡。所以这种情况我们需要做两次旋转。

代码:
rotationLR(node) {node.left = this.rotationRR(node.left);return this.rotationLL(node);
}第四种情况:右侧子节点的高度高于左侧子节点,并且右侧子节点左侧较重。这种情况下我们可以对右侧子节点进行有旋转来修复。然后再对不平衡节点进行一个左旋转来修复。

向AVL树中插入节点
前面讲解了这么多树的旋转,就是为了服务于AVL树中节点的增删。
步骤很简单,每当我们向AVL树里插入或删除一个节点,便执行平衡性检查。平衡性不通过,便旋转树。
const BalanceFactor = {UNBALANCED_RIGHT: 1,SLIGHTLY_UNBALANCED_RIGHT: 2,BALANCED: 3,SLIGHTLY_UNBALANCED_LEFT: 4,UNBALANCED_LEFT: 5
};
getBalanceFactor(node) {const heightDifference = this.getNodeHeight(node.left) - this.getNodeHeight(node.right);switch (heightDifference) {case -2:return BalanceFactor.UNBALANCED_RIGHT;case -1:return BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT;case 1:return BalanceFactor.SLIGHTLY_UNBALANCED_LEFT;case 2:return BalanceFactor.UNBALANCED_LEFT;default:return BalanceFactor.BALANCED;}
}·左子树高度-右子树高度。当差值为0(default)或-1或1,都属于平衡范围。而2和-2则已经不平衡。-1和1方便让我们辨别哪侧子树较重。
insert(key) {this.root = this.insertNode(this.root, key);}insertNode(node, key) {if (node == null) {return new Node(key);} else if (this.compareFn(key, node.key) === Compare.LESS_THAN) {node.left = this.insertNode(node.left, key);} else if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) {node.right = this.insertNode(node.right, key);} else {return node; // duplicated key}// verify if tree is balancedconst balanceFactor = this.getBalanceFactor(node);if (balanceFactor === BalanceFactor.UNBALANCED_LEFT) {if (this.compareFn(key, node.left.key) === Compare.LESS_THAN) {// Left left casenode = this.rotationLL(node);} else {// Left right casereturn this.rotationLR(node);}}if (balanceFactor === BalanceFactor.UNBALANCED_RIGHT) {if (this.compareFn(key, node.right.key) === Compare.BIGGER_THAN) {// Right right casenode = this.rotationRR(node);} else {// Right left casereturn this.rotationRL(node);}}return node;}从AVL树里移除节点
removeNode(node, key) {node = super.removeNode(node, key); // {1}if (node == null) {return node;}// verify if tree is balancedconst balanceFactor = this.getBalanceFactor(node);if (balanceFactor === BalanceFactor.UNBALANCED_LEFT) {// Left left caseif (this.getBalanceFactor(node.left) === BalanceFactor.BALANCED ||this.getBalanceFactor(node.left) === BalanceFactor.SLIGHTLY_UNBALANCED_LEFT) {return this.rotationLL(node);}// Left right caseif (this.getBalanceFactor(node.left) === BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT) {return this.rotationLR(node.left);}}if (balanceFactor === BalanceFactor.UNBALANCED_RIGHT) {// Right right caseif (this.getBalanceFactor(node.right) === BalanceFactor.BALANCED ||this.getBalanceFactor(node.right) === BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT) {return this.rotationRR(node);}// Right left caseif (this.getBalanceFactor(node.right) === BalanceFactor.SLIGHTLY_UNBALANCED_LEFT) {return this.rotationRL(node.right);}}return node;}相关文章:

JS算法与树(二)
前言 二叉搜索树(BST)存在一个问题:当你添加的节点数够多的时候,树的一边可能会非常的深。而其他的分支却只有几层。 AVL树 为了解决上面的问题,我们提出一种自平衡二叉搜索树。意思是任何一个节点左右两侧子树的高度之…...

composer 扩展库。助手库文档
composer helpers packagist 简介 death_satan/composer 作用于在有composer管理工具的项目中。封装了上层由 composer V2 提供的 ClassLoader 和 InstallVersion 轻量级的封装,无任何第三方包集成。便捷式的使用composer V2 API 安装要求 php > 7.4composer &g…...

Web弹性布局
/*弹性盒子 弹性布局 */ /* 默认从左到右 */ display: flex; /* 从右到左 */ /* flex-direction: row-reverse; */ /* 从上到下 */ /* flex-direction: column; */ …...

基于深度学习的AI生成式人脸图像鉴别
AIGC(AI内容生成)技术的快速发展确实为创作者提供了高效生产力工具,但同时也引发了一些问题和挑战。这些技术可以生成以假乱真的图像、视频换脸等,给不法分子提供了滥用的机会。其中,一些不法分子可能利用AIGC技术制造…...
iOS开发Swift-1-Xcode创建项目
1.创建项目 双击Xcode App,选择Create a new Xcode project。 选择创建一个iOS普通的App项目。选择Single View App,点击Next。 填写项目名,组织名称等,点击next。 选择好文件的存储路径,点击create。 2.为前端添加组件…...

AI 领域中 SLAM、Planning 和 Perception 的区别和联系
在人工智能(AI)领域,SLAM、Planning 和 Perception 是三个关键的概念,它们在机器人、自主驾驶车辆等领域中扮演着重要的角色。以下是它们之间的区别和联系: SLAM SLAM(Simultaneous Localization and Map…...

【数据库】MySQL基础知识全解
系列综述: 💞目的:本系列是个人整理为了秋招面试的,整理期间苛求每个知识点,平衡理解简易度与深入程度。 🥰来源:材料主要源于拓跋阿秀、小林coding等大佬博客进行的,每个知识点的修…...
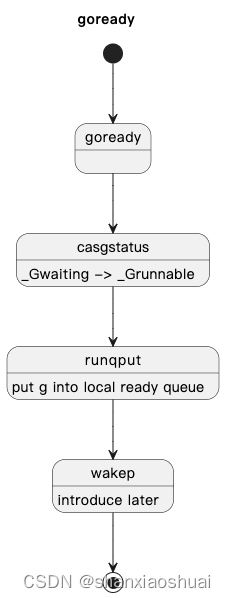
【golang】调度系列之goroutine
前面的两篇,从相对比较简单的锁的内容入手(也是干货满满),开始了go的系列。这篇开始,进入更核心的内容。我们知道,go应该是第一门在语言层面支持协程的编程语言(可能是我孤陋寡闻),goroutine也完全算的上是go的门面。g…...

A 股个股资金流 API 数据接口
A 股个股资金流 API 数据接口 全量股票资金流数据,全量A股数据,最长30日历史数据 1. 产品功能 支持所有A股资金流数据查询;每日定时更新数据;支持多达 30 日历史数据查询;超高的查询效率,数据秒级返回&am…...
【前端】Layui动态数据表格拖动排序
目录 一、下载layui-soul-table 二、使用 三、Layui实际使用 1、html代码 2、JS代码 3、PHP后台代码 目的:使用Layui的数据表格,拖动行进行排序。 使用插件:layui-soul-table 和 Layui 1.layui-soul-table文档:https://…...

Linux 忘记密码解决方法
很多朋友经常会忘记Linux系统的root密码,linux系统忘记root密码的情况该怎么办呢?重新安装系统吗?答案是不需要进入单用户模式更改一下root密码即可。 步骤如下: 重启linux系统 3 秒之内要按一下回车,出现如下界面 …...
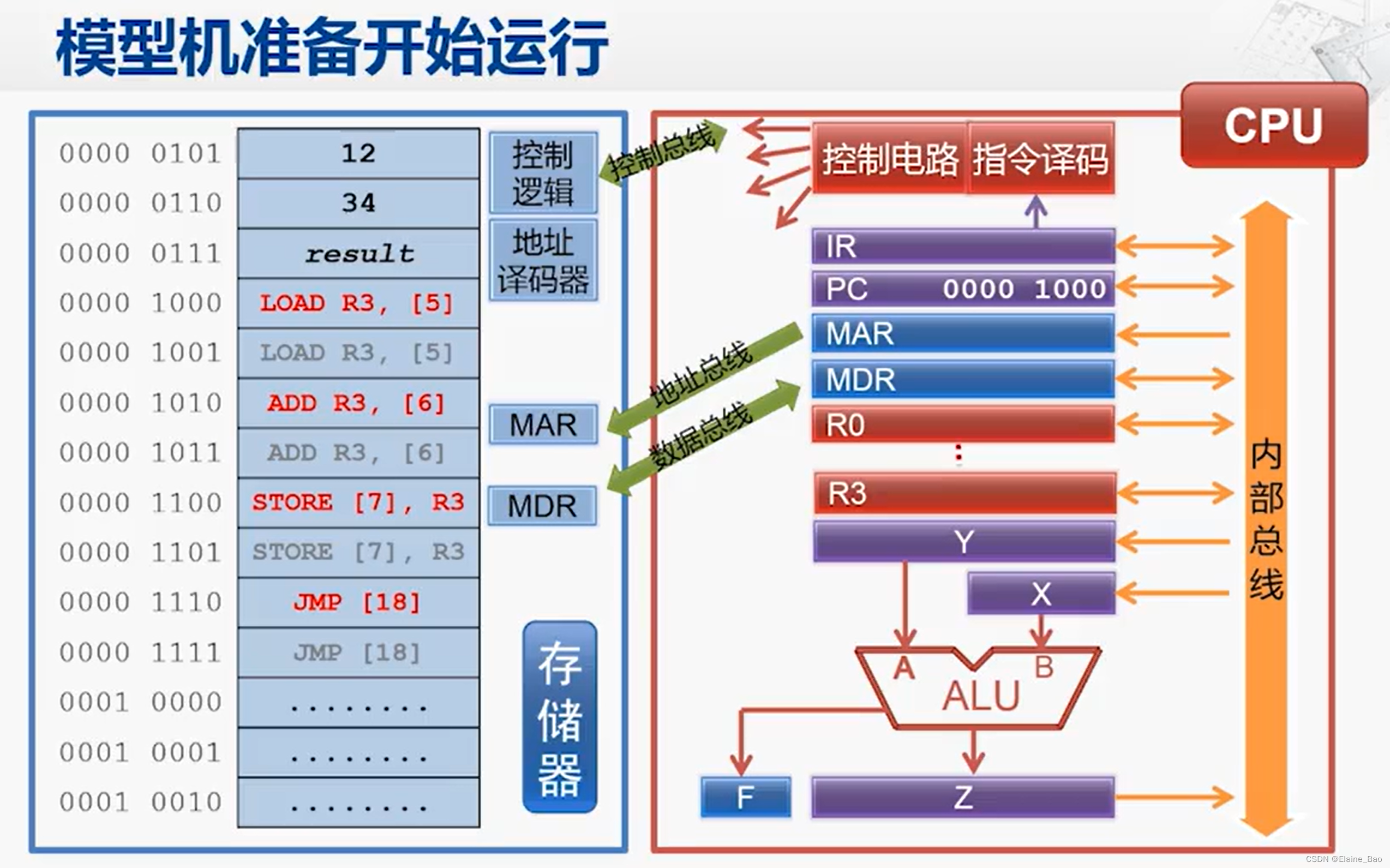
【计算机组成 课程笔记】2.1 设计自己的计算机
课程链接: 计算机组成_北京大学_中国大学MOOC(慕课) 2 - 1 - 201-设计自己的计算机(14‘24’‘)_哔哩哔哩_bilibili 什么是指令系统体系结构?这个问题其实非常简单,但要想解释清楚也没有那么容易。我们还是从一个小故事…...

vb房屋销售管理系统设计与实现
摘 要 当今社会经济高速发展,人们的生活节奏日益加快。随着人们生活水平的提高,相应地人们对住房的需求也随之增大,对于购房者来说,如何在琳琅满目的商品房中方便快捷的选择到自己称心如意的家居便成了一个难题;对于房屋开发商和销售商来说,如何对众多的房屋产品进行科…...
_Zipkin使用SpringCloud Stream以及Elasticsearch)
SpringCloud学习笔记(十三)_Zipkin使用SpringCloud Stream以及Elasticsearch
在前面的文章中,我们已经成功的使用Zipkin收集了项目的调用链日志。但是呢,由于我们收集链路信息时采用的是http请求方式收集的,而且链路信息没有进行保存,ZipkinServer一旦重启后就会所有信息都会消失了。基于性能的考虑…...

重仓“AI”的百度迎来收获季?
今年以来,由AIGC引发的“行业旋风”持续席卷各行各业,给沉闷已久的互联网赛道带来了一股暖流。这场AI旋风对于重仓押注AI的玩家而言,更是如同“久旱逢甘霖”,终于迎来了“柳暗花明”的一天。 作为重仓押注AI赛道的头部玩家&#x…...

Linux 通过 Docker 部署 Nacos 2.2.3 服务发现与配置中心
目录 环境准备Nacos 数据库创建Docker 部署 Nacos1. 创建挂载目录2. 下载镜像3. 创建和启动容器4. 访问控制台 导入 Nacos 配置SpringBoot 整合 Nacospom 依赖application.yml 配置 参考官方链接微服务商城源码 环境准备 名称版本IP端口Nacos2.2.3192.168.10.218848、9848MySQ…...

macOS上制作arm64的jdk17镜像
公司之前一直用的openjdk17的镜像,docker官网可以直接下载,但是最近对接的一个项目,对方用的是jdk17,在对接的时候有加解密异常的问题,为了排查是不是jdk版本的问题,需要制作jdk17的镜像。docker官网上的第…...

对话永洪科技CEO何春涛:专注BI,决胜AI时代丨数据猿专访
大数据产业创新服务媒体 ——聚焦数据 改变商业 大数据、云计算、人工智能为代表的新一代信息技术走向普及,数据驱动业务,逐渐成为现代化企业管理、运作的日常。对于年均复合增长率超过20%的国内商业智能(BI)市场而言,…...

Redis 数据类型详细解析
Redis是一个开源的、内存中的数据结构存储系统,可用作数据库、缓存和消息代理。Redis支持多种类型的数据结构,包括字符串(String)、哈希(Hashes)、列表(Lists)、集合(Set…...

NOR型flash vs NAND型flash
FLASH是一种存储芯片,全名叫Flash EEPROM Memory,通过程序可以修改数据,即平时所说的“闪存”。 闪存可以在软件的控制下写入和擦写数据。其存储空间被分割成相对较大的可擦除单元,成为擦除块(erase block)…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
