红外物理学习笔记 ——第三章
第三章
基尔霍夫定律:就是说物体热平衡条件下,发射的辐射功率要等于吸收的辐射功率
M = α E M=\alpha E M=αE
α \alpha α 是吸收率, M M M 是幅出度(发射出去的), E E E是辐照度(外面照过来的)
普朗克公式: 描述了黑体光谱幅出度关于 温度 和 波长 的关系
M λ b b = c 1 λ 5 1 e c 2 / λ T − 1 M_{\lambda bb}= \frac{c_1}{\lambda ^5} \frac{1}{e^{c_2/\lambda T}-1} Mλbb=λ5c1ec2/λT−11
c 1 , c 2 c_1,c_2 c1,c2 分别为第一、第二辐射常数
薇恩位移定律: 普朗克公式里面不是有两个变量吗,而且其图像都是先上升后下降,有一个峰值波长(平的,导数为0),所以你把普朗克公式对波长求个导,导数为0 就是,峰值波长了。薇恩位移定律可以通过温度确定峰值波长
λ m T = 2898.8 \lambda_m T = 2898.8 λmT=2898.8
PS: 把这东西带入普朗克公式可以得到黑体光谱幅出度的峰值
斯特藩-波尔兹曼定律: 他的意思就是说,你把普朗克公式对波长进行积分,就得到了全波长下黑体光谱幅出度关于温度的一个表达式
M b b = σ T 4 M_{bb}= \sigma T^4 Mbb=σT4
σ \sigma σ 是个常数
黑体辐射的简易计算: 本来嘛,只要有了具体的 温度 和 波长 ,直接套公式就行,但是有次方,有指数,计算比较麻烦。所以引入了两个函数(都是关于 温度 和 波长 )简便计算。
- f 函数,用来简便计算特定温度下,特定波长的辐出度
M λ = f ( λ ⋅ T ) M λ m = f ( λ ⋅ T ) ⋅ b 1 T 5 M_{\lambda} = f(\lambda \cdot T) M_{\lambda_{m}} = f(\lambda \cdot T) \cdot b_1 T^5 Mλ=f(λ⋅T)Mλm=f(λ⋅T)⋅b1T5
M λ m = b 1 T 5 M_{\lambda_{m}} = b_1 T^5 Mλm=b1T5 是之前提到的幅出度的峰值,可由维恩位移定律带入普朗克公式得到
- F 函数,用来计算任意波长范围的辐出度
M 0 − λ = F ( λ ⋅ T ) M 0 − ∞ = F ( λ ⋅ T ) ⋅ σ T 4 M_{0 - \lambda } = F(\lambda \cdot T) M_{0 - \infty} = F(\lambda \cdot T) \cdot \sigma T^4 M0−λ=F(λ⋅T)M0−∞=F(λ⋅T)⋅σT4
M λ 1 − λ 2 = M 0 − λ 2 − M 0 − λ 1 = [ F ( λ 2 ⋅ T ) − F ( λ 1 ⋅ T ) ] ⋅ σ T 4 M_{\lambda_1 - \lambda_2 } =M_{0 - \lambda_2 } - M_{0 - \lambda_1 }= [F(\lambda_2 \cdot T)- F(\lambda_1 \cdot T)] \cdot \sigma T^4 Mλ1−λ2=M0−λ2−M0−λ1=[F(λ2⋅T)−F(λ1⋅T)]⋅σT4
工程最佳温度: 前面的学习我们知道给定温度可以得到一个峰值波长,给定波长也可以得到一个最佳温度,但是工程上的最佳温度和韦恩定律得出的并不相同。
λ e T e = 3669.73 \lambda_e T_e = 3669.73 λeTe=3669.73
T e = 1.266 T m T_e = 1.266 T_m Te=1.266Tm
最大对比度: 就是说想让目标和背景获得最大的可区分度,波长选多少合适
λ c T e = 2411 \lambda_c T_e = 2411 λcTe=2411
λ c = 0.832 λ m \lambda_c = 0.832 \lambda_m λc=0.832λm
发射率 ε \varepsilon ε: 用来衡量实际物体和黑体的接近程度,其实就是在给定温度 T T T 下,实际物体的辐射量比上黑体的辐射量,这个值越接近于1越好。
辐射温度、色温度、亮温度。在知道发射率的情况下,都可以算出真实温度。
相关文章:

红外物理学习笔记 ——第三章
第三章 基尔霍夫定律:就是说物体热平衡条件下,发射的辐射功率要等于吸收的辐射功率 M α E M\alpha E MαE α \alpha α 是吸收率, M M M 是幅出度(发射出去的), E E E是辐照度(外面照过来的…...

使用 htmx 构建交互式 Web 应用
学习目标:了解htmx的基本概念、特点和用法,并能够运用htmx来创建交互式的Web应用程序。 学习内容: 1. 什么是htmx? - htmx是一种用于构建交互式Web应用程序的JavaScript库。 - 它通过将HTML扩展为一种声明性的交互式语言&a…...
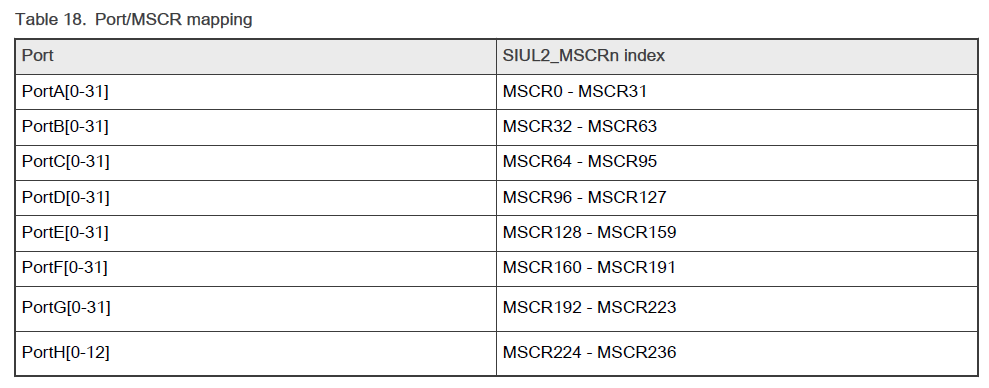
S32K324芯片学习笔记
文章目录 Core and architectureDMASystem and power managementMemory and memory interfacesClocksSecurity and integrity安全与完整性Safety ISO26262Analog、Timers功能框图内存mapflash Signal MultiplexingPort和MSCR寄存器的mapping Core and architecture 两个Arm Co…...

htmx-使HTML更强大
本文作者是360奇舞团开发工程师 htmx 让我们先来看一段俳句: javascript fatigue: longing for a hypertext already in hand 这个俳句很有意思,是开源项目htmx文档中写的,意思是说,我们已经有了超文本,为什么还要去使用javascr…...
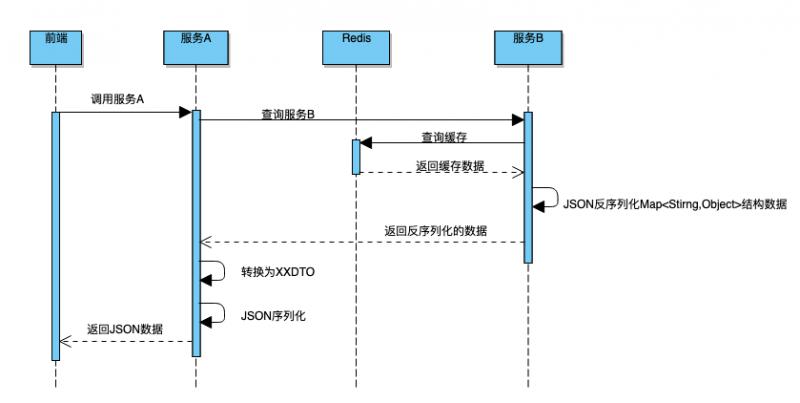
Java学习之序列化
1、引言 《手册》第 9 页 “OOP 规约” 部分有一段关于序列化的约定 1: 【强制】当序列化类新增属性时,请不要修改 serialVersionUID 字段,以避免反序列失败;如果完全不兼容升级,避免反序列化混乱,那么请…...
C++实现蜂群涌现效果(flocking)
Flocking算法0704_元宇宙中的程序员的博客-CSDN博客 每个个体的位置,通过计算与周围个体的速度、角度、位置,去更新位置。...
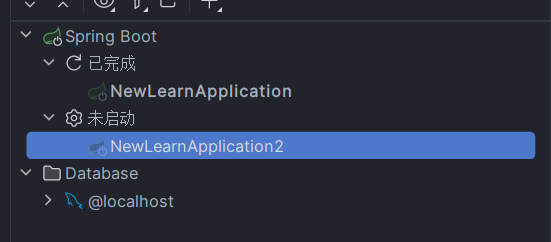
IDEA复制一个工程为多个并启动,测试负载均衡
1 找到服务按钮 2 选择复制配置 3 更改新的名称与虚拟机参数 复制下面的代码在VM参数中 -Dserver.port8082 4 最后启动即可...

001_C++语法基础
C语法基础 所有C语法要用英文区分大小写每个语句写完以分号结束 C标准输入输出头文件iostream 若想通过C实现数据的输入和输出,需要导入标准输入输出头文件 #include <iostream>标准输入输出头文件<iostream>中包含了cin输入语句和cout输出语句 标…...
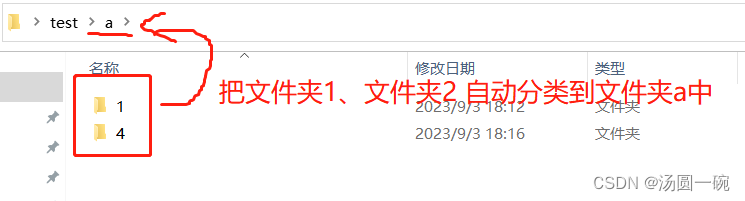
对Excel表中归类的文件夹进行自动分类
首先把excel表另存为.txt文件(注意:刚开始可能是ANSI格式,需要转成UTF-8格式);再新建一个.txt文件,重命名成.bat文件(注意:直接创建的如果是是UTF-8格式,最好转成ANSI格式࿰…...
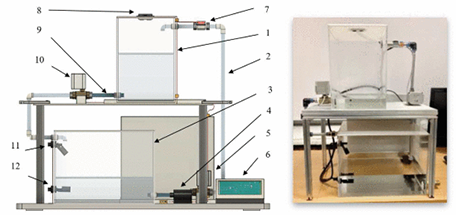
LabVIEW液压支架控制系统的使用与各种配置的预测模型的比较分析
LabVIEW液压支架控制系统的使用与各种配置的预测模型的比较分析 模型预测控制在工业中应用广泛。这种方法的优点之一是在求解最优控制问题时能够明确考虑对输入和输出状态施加的约束。控制对象模型用于有限时间范围内最优控制的实时计算。所使用的数学设备允许从具有单输入和单…...

C++中位运算符使用
& 与 只有都为1结果为1 0 & 0 00 & 1 01 & 0 01 & 1 1 | 或 只要一个为1结果为1 0|00 0|11 1|01 1|11 ^ 异或 两个相同的数字为0,其余为1 0^00 1^01 0^11 1^10 ~ 取反 将进制位数进行取反 ~1-2 //0000 0001-->代…...

微机原理 || 第2次测试:汇编指令(加减乘除运算,XOR,PUSH,POP,寻址方式,物理地址公式,状态标志位)(测试题+手写解析)
(一)测试题目: 1.数[X]补1111,1110B,则其真值为 2.在I/O指令中,可用于表示端口地址的寄存器 3. MOV AX,[BXSl]的指令中,源操作数的物理地址应该如何计算 4.执行以下两条指令后,标志寄存器FLAGS的六个状态…...

人员闯入检测告警算法
人员闯入检测告警算法通过yolov5网络模型识别检测算法,人员闯入检测告警算法对未经许可或非法进入的人员进行及时识别告警,确保对危险区域的安全管理和保护。YOLO系列算法是一类典型的one-stage目标检测算法,其利用anchor box将分类与目标定位…...
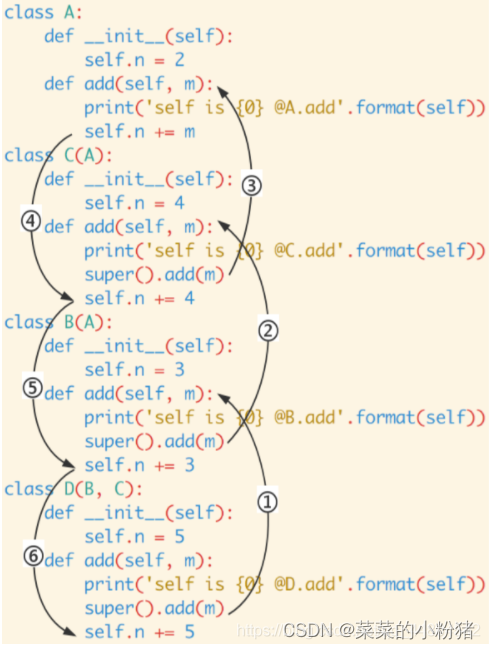
python中super()用法
super关键字的用法 一、概述二、作用三、语法四、使用示例1.通过super() 来调用父类的__init__ 构造方法:2.通过supper() 来调用与子类同名的父类方法2.1 单继承2.2 多继承 一、概述 super() 是python 中调用父类(超类)的一种方法࿰…...
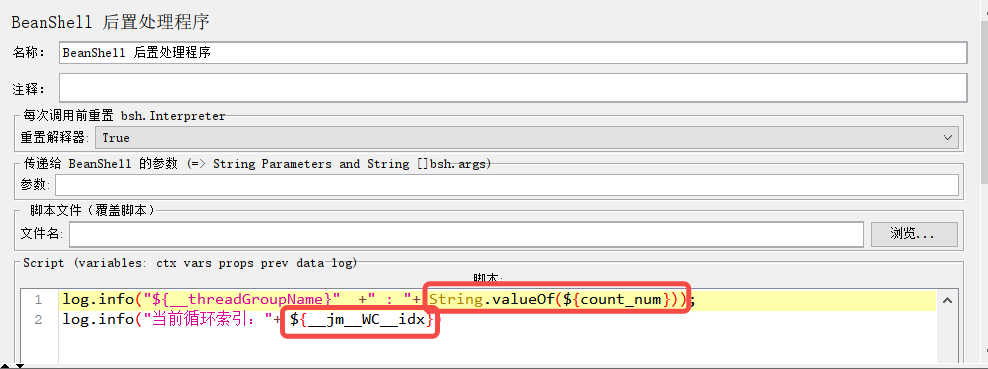
jmeter While控制器
一种常见的循环控制语句,用于重复执行一段代码块,直到指定的条件不再满足。 参数: 空LASTJMeter变量、函数、属性或任意其他可用表达式 (jmeter提供的方法)。判断变量值count_num小于等于20,推荐简单的几…...

3D数字孪生技术助力港口全新升级,提供实时数据进行智能调度
港口3D数字孪生平台是一种基于数字技术的虚拟模型,它可以模拟真实的港口环境,并对港口的运营、管理、安全等方面进行实时监控和优化。该平台带来了许多智能化提升,包括以下几个方面: 一、自动化操作和智能调度 数字孪生平台可以通…...
Qt日历控件示例-QCalendarWidget
基本说明 QCalendarWidget介绍: QCalendarWidget 是 Qt 框架中提供的一个日期选择控件,用户可以通过该控件快速选择需要的日期,并且支持显示当前月份的日历。 这里,我们继承了QCalendarWidget,做了一些简单封装和样式调整 1.使用的IDE&…...
Stream流使用)
函数式编程(四)Stream流使用
一、概述 在使用stream之前,先理解Optional 。 Optional是Java 8引入的一个容器类,用于处理可能为空的值。它提供了一种优雅的方式来处理可能存在或不存在的值,避免了空指针异常。 Optional的主要特点如下: 可能为空ÿ…...

区块链面临六大安全问题 安全测试方案研究迫在眉睫
区块链面临六大安全问题 安全测试方案研究迫在眉睫 近年来,区块链技术逐渐成为热门话题,其应用前景受到各国政府、科研机构和企业公司的高度重视与广泛关注。随着技术的发展,区块链应用与项目层出不穷,但其安全问题不容忽视。近年…...

K8S---kubelet TLS 启动引导
一、引导启动初始化过程(Bootstrap Initialization ) 1、kubeadm 生成一个Token,类似07401b.f395accd246ae52d这种格式,或者自己手动生成2、使用kubectl命令行,生成一个Secret,具体详见认证、授权3、kubelet 进程启动 (begin)4、kubelet 看到自己没有对应的 kubeconfig…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
