【LeetCode每日一题合集】2023.8.7-2023.8.13(动态规划分治)
文章目录
- 344. 反转字符串
- 1749. 任意子数组和的绝对值的最大值(最大子数组和)
- 1281. 整数的各位积和之差
- 1289. 下降路径最小和 II
- 1572. 矩阵对角线元素的和
- 解法1——加的时候判断
- 解法2——加完之后判断
- 23. 合并 K 个升序链表
- 解法1——使用优先队列合并
- 解法2——分治合并⭐
- 88. 合并两个有序数组
- 解法——逆向双指针
344. 反转字符串
https://leetcode.cn/problems/reverse-string/description/
要求原地修改,使用双指针两两交换位置就好了。
class Solution {public void reverseString(char[] s) {for (int l = 0, r = s.length - 1; l < r; ++l, --r) {char t = s[l];s[l] = s[r];s[r] = t;}}
}
1749. 任意子数组和的绝对值的最大值(最大子数组和)
https://leetcode.cn/problems/maximum-absolute-sum-of-any-subarray/description/
提示:
1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
参考最大子数组和那道题。
这道题的区别就是维护一个最大值和一个最小值,更新答案时用最大值和最小值取反来更新答案。
class Solution {public int maxAbsoluteSum(int[] nums) {int mx = 0, mn = 0, ans = 0;for (int num: nums) {mx = mx + num < num? num: mx + num;mn = mn + num > num? num: mn + num;ans = Math.max(ans, Math.max(mx, -mn));}return ans;}
}
1281. 整数的各位积和之差
1281. 整数的各位积和之差
提示:
1 <= n <= 10^5
模拟即可。
class Solution {public int subtractProductAndSum(int n) {int mul = 1, sum = 0;while (n != 0) {int v = n % 10;n /= 10;mul *= v;sum += v;}return mul - sum;}
}
1289. 下降路径最小和 II
https://leetcode.cn/problems/minimum-falling-path-sum-ii/description/
提示:
n == grid.length == grid[i].length
1 <= n <= 200
-99 <= grid[i][j] <= 99
解法1——动态规划 O ( n 3 ) O(n^3) O(n3)
从数据范围来看,可以使用 O ( n 3 ) O(n^3) O(n3)的算法。
对于每个位置,选择上一行中最小的那个位置递推过来即可。
class Solution {public int minFallingPathSum(int[][] grid) {int m = grid.length, n = grid[0].length;// 枚举第1~m-1行for (int i = 1; i < m; ++i) {// 枚举当前行的0~n-1列for (int j = 0; j < n; ++j) {// 枚举上一行的0~n-1列,选出其中最小的int v = Integer.MAX_VALUE;for (int k = 0; k < n; ++k) {if (k != j) v = Math.min(v, grid[i - 1][k]);}grid[i][j] += v;}}return Arrays.stream(grid[m - 1]).min().getAsInt();}
}
解法2——转移过程优化 O ( n 2 ) O(n^2) O(n2) ⭐
在状态转移的过程中可以发现,第 i 行的很多位置是从 i - 1 行的同一列转移过来的,因为他们都会优先选择第 i - 1 行的最小值,只有当列相同时才会去选择次小值。
因此我们只需要维护三个变量:最小值、最小值对应的列、次小值 即可,不需要完整枚举上一行的每一列。
class Solution {public int minFallingPathSum(int[][] grid) {int n = grid.length;int mn = 0, mn2 = 0, mnId = -1;// 枚举每一行for (int i = 0; i < n; ++i) {// 当前行的最小值、次小值、最小值下标int curMn = Integer.MAX_VALUE, curMn2 = Integer.MAX_VALUE, curMnId = -1;// 枚举每一列for (int j = 0; j < n; ++j) {int curSum = (j != mnId? mn: mn2) + grid[i][j];// 使用当前和更新最小值和次小值if (curSum < curMn) {curMn2 = curMn;curMn = curSum;curMnId = j;} else if (curSum < curMn2) {curMn2 = curSum;}}// 更新上一行的最小值、次小值、最小值下标mn = curMn;mn2 = curMn2;mnId = curMnId;}return mn;}
}
优化之后,执行用时从 32ms 变成了 1ms。效果显著。
1572. 矩阵对角线元素的和
https://leetcode.cn/problems/matrix-diagonal-sum/
提示:
n == mat.length == mat[i].length
1 <= n <= 100
1 <= mat[i][j] <= 100
解法1——加的时候判断
class Solution {public int diagonalSum(int[][] mat) {int n = mat.length, ans = 0;for (int i = 0; i < n; ++i) {ans += mat[i][i];if (n - 1 - i != i) ans += mat[i][n - 1 - i];}return ans;}
}
解法2——加完之后判断
循环里面不用写 if 了,最后判断一下 n 是奇数还是偶数就好了。
class Solution {public int diagonalSum(int[][] mat) {int n = mat.length, ans = 0;for (int i = 0; i < n; ++i) {ans += mat[i][i] + mat[i][n - 1 - i];}return ans - mat[n / 2][n / 2] * (n & 1);}
}
23. 合并 K 个升序链表
https://leetcode.cn/problems/merge-k-sorted-lists/
提示:
k == lists.length
0 <= k <= 10^4
0 <= lists[i].length <= 500
-10^4 <= lists[i][j] <= 10^4
lists[i] 按 升序 排列
lists[i].length 的总和不超过 10^4
解法1——使用优先队列合并
将 k 个链表放入优先队列中,每次取出最小的,使用后再将其 next 节点放入优先队列即可。
class Solution {public ListNode mergeKLists(ListNode[] lists) {PriorityQueue<ListNode> pq = new PriorityQueue<>((a, b) -> a.val - b.val);for (ListNode list: lists) {if (list != null) pq.offer(list);}ListNode dummy = new ListNode(-1), prev = dummy;while (!pq.isEmpty()) {ListNode cur = pq.poll();prev.next = cur;prev = cur;if (cur.next != null) pq.offer(cur.next);} return dummy.next;}
}
解法2——分治合并⭐
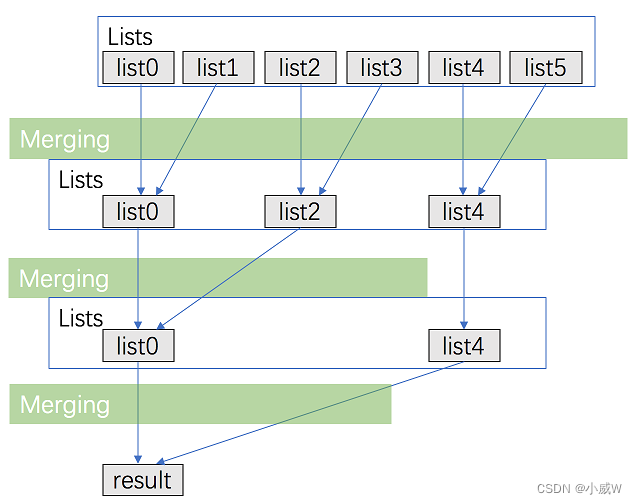
类似于归并排序时使用的思想,两两处理,向上归并。
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode mergeKLists(ListNode[] lists) {return mergeKLists(lists, 0, lists.length);}public ListNode mergeKLists(ListNode[] lists, int i, int j) {int m = j - i; // 这段区间的长度if (m == 0) return null;if (m == 1) return lists[i];// 分成左右两个区间处理ListNode left = mergeKLists(lists, i, i + m / 2);ListNode right = mergeKLists(lists, i + m / 2, j);return mergeTwoLists(left, right);}public ListNode mergeTwoLists(ListNode list1, ListNode list2) {ListNode dummy = new ListNode(); // 用哨兵节点简化代码逻辑ListNode cur = dummy;while (list1 != null && list2 != null) {if (list1.val < list2.val) {cur.next = list1;list1 = list1.next;} else {cur.next = list2;list2 = list2.next;}cur = cur.next;}cur.next = list1 != null? list1: list2;return dummy.next;}
}
这两种解法的时间复杂度都是 O ( n ∗ log k ) O(n*\log{k}) O(n∗logk)
88. 合并两个有序数组
https://leetcode.cn/problems/merge-sorted-array/
提示:
nums1.length == m + n
nums2.length == n
0 <= m, n <= 200
1 <= m + n <= 200
-10^9 <= nums1[i], nums2[j] <= 10^9
进阶:你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗?
解法——逆向双指针
class Solution {public void merge(int[] nums1, int m, int[] nums2, int n) {int i = m - 1, j = n - 1, k = m + n - 1;while (i >= 0 && j >= 0) {if (nums1[i] >= nums2[j]) nums1[k--] = nums1[i--];else nums1[k--] = nums2[j--];}while (i >= 0) nums1[k--] = nums1[i--];while (j >= 0) nums1[k--] = nums2[j--];}
}
相关文章:

【LeetCode每日一题合集】2023.8.7-2023.8.13(动态规划分治)
文章目录 344. 反转字符串1749. 任意子数组和的绝对值的最大值(最大子数组和)1281. 整数的各位积和之差1289. 下降路径最小和 II解法1——动态规划 O ( n 3 ) O(n^3) O(n3)解法2——转移过程优化 O ( n 2 ) O(n^2) O(n2) ⭐ 1572. 矩阵对角线元素的和解法…...

微信小程序修改vant组件样式
1 背景 在使用vant组件开发微信小程序的时候,想更改vant组件内部样式,达到自己想要的目的(van-grid组件改成宫格背景色为透明,默认为白色),官网没有示例,通过以下几步修改成功。 2 步骤 2.1 …...

yum 、rpm、yumdownloader、repotrack 学习笔记
1 Linux 包管理器概述 rpm的使用: rpm -ivh filename.rpm#这列出该packageName(包名)安装的所有文件列表。 rpm -ql packageName #查询已安装的该packageName的详细信息,包括版本、发布日期等。 rpm -qi packageName #列出该pac…...

python检测CPU占用、内存和磁盘剩余空间 脚本
python检测CPU占用、内存和磁盘剩余空间 脚本。后续将其加入到计划列表中即可 # codingutf-8 import time import psutil import osimport smtplibfrom email.mime.multipart import MIMEMultipart from email.mime.text import MIMEText # email 用于构建邮件内容 from email…...

量化策略:CTA,市场中性,指数增强
CTA 策略 commodity Trading Advisor Strategy,即“商品交易顾问策略”,也被称作管理期货策略。 期货T0,股票T1双向交易:就单向交易而言的,不仅能先买入再卖出(做多),而且可以先卖…...
 测试点全过)
L1-051 打折(Python实现) 测试点全过
前言: {\color{Blue}前言:} 前言: 本系列题使用的是,“PTA中的团体程序设计天梯赛——练习集”的题库,难度有L1、L2、L3三个等级,分别对应团体程序设计天梯赛的三个难度。更新取决于题目的难度,…...
任意文件读取和漏洞复现
任意文件读取 1. 概述 一些网站的需求,可能会提供文件查看与下载的功能。如果对用户查看或下载的文件没有限制或者限制绕过,就可以查看或下载任意文件。这些文件可以是漂代码文件,配置文件,敏感文件等等。 任意文件读取会造成&…...
编译KArchive在windows10下
使用QT6和VS2019编译KArchive的简要步骤: 安装 Qt ,我是用源码自己编译的 "F:\qtbuild"安装CMakefile并配置环境变量安装Git下载ECM源码 https://github.com/KDE/extra-cmake-modules.git-------------------------------------------------…...

【Python】批量下载页面资源
【背景】 有一些非常不错的资源网站,比如一些MP3资源网站。资源很丰富,但是每一个资源都不大,一个一个下载费时费力,想用Python快速实现可复用的批量下载程序。 【思路】 获得包含资源链接的静态页面,用beautifulsoup分析页面,获得所有MP3资源的实际地址,然后下载。…...
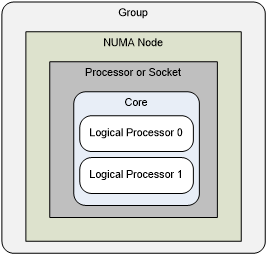
Windows NUMA编程实践 – 处理器组、组亲和性、处理器亲和性及版本变化
Windows在设计之初没有考虑过对大数量的多CPU和NUMA架构的设备的支持,大部分关于CPU的设计按照64个为上限来设计。核心数越来越多的多核处理器的进入市场使得微软不得不做较大的改动来进行支持,因此Windows 的进程、线程和NUMA API在各个版本中行为不一样…...
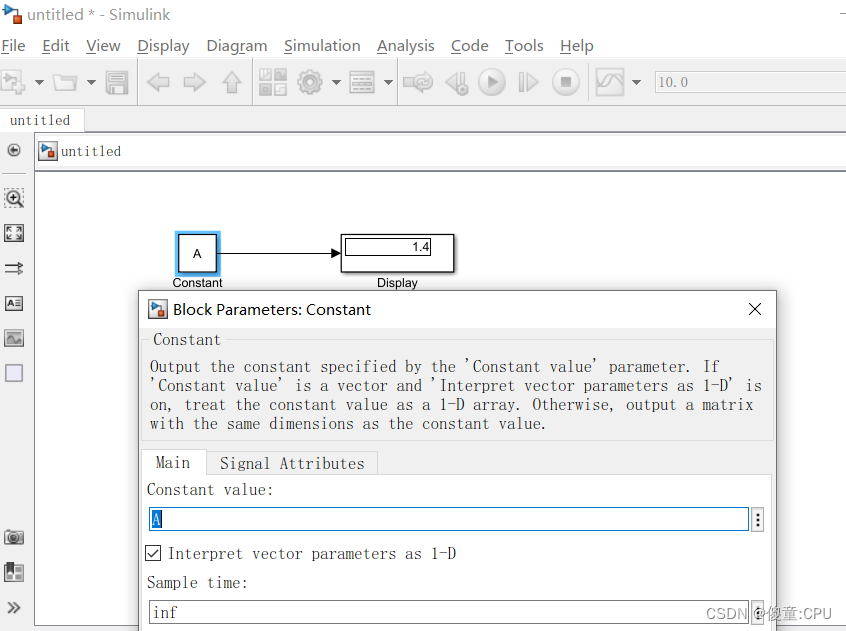
MATLAB中编译器中的变量联系到Simulink
MATLAB中编译器中的变量联系到Simulink 现在编译器中创建变量,进行编译,使其生成在工作区。 然后在Simulink中国使用变量即可。...

开展自动化方案时,需要考虑哪些内容,开展实施前需要做哪些准备呢?
在开展软件自动化测试方案时,需要考虑以下方面: 选择合适的自动化测试工具:根据项目的需求和技术栈选择适合的自动化测试工具,如Selenium、Appium、Jenkins等。确定自动化测试范围:明确需要自动化的功能模块和业务场景…...

进程、线程、内存管理
目录 进程和线程区别 进程和线程切换的区别 系统调用流程 系统调用是否会引起线程切换 为什么需要使用虚拟内存 进程和线程区别 本质区别: 进程是资源分配的基本单元。 线程是操作系统调度的基本单元。 地址空间: 进程具有独立的虚拟地址空间。 线程…...
设计模式系列-创建者模式
一、上篇回顾 上篇我们主要讲述了抽象工厂模式和工厂模式。并且分析了该模式的应用场景和一些优缺点,并且给出了一些实现的思路和方案,我们现在来回顾一下: 抽象工厂模式:一个工厂负责所有类型对象的创建,支持无缝的新增新的类型对…...

加工生产调度
题目描述 某工厂收到了 n 个产品的订单,这 n 个产品分别在 A、B 两个车间加工,并且必须先在 A 车间加工后才可以到 B 车间加工。 某个产品 在 A,B 两车间加工的时间分别为 。怎样安排这 n 个产品的加工顺序,才能使总的加工时间…...
Hadoop 集群小文件归档 HAR、小文件优化 Uber 模式
文章目录 小文件归档 HAR小文件优化 Uber 模式 小文件归档 HAR 小文件归档是指将大量小文件合并成较大的文件,从而减少存储开销、元数据管理的开销以及处理时的任务调度开销。 这里我们通过 Hadoop Archive (HAR) 来进行实现,它是一种归档格式…...

Android OkHttp源码阅读详解一
博主前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住也分享一下给大家 👉点击跳转到教程 前言:源码阅读基于okhttp:3.10.0 Android中OkHttp源码阅读二(责任链模式) implementation com.squareup.o…...

UG\NX CAM二次开发 查询工序所在的方法组TAG UF_OPER_ask_method_group
文章作者:代工 来源网站:NX CAM二次开发专栏 简介: UG\NX CAM二次开发 查询工序所在的方法组TAG UF_OPER_ask_method_group 效果: 代码: void MyClass::do_it() { int count=0;tag_t * objects;UF_UI_ONT_ask_selected_nodes(&count, &objects);for (i…...

npm获取函数名称和测试js脚本
这边遇到一个类似于测试的需求,需要从一个js文件里获取函数名,然后尝试执行这些函数和创建实例。这边首先遇到了一个问题是如何动态获取js里的函数名和类名,我这边暂时没找到特别好的方法,已有的方法都是类似于提取语法树那种提取…...

ISO/IEC/ITU标准如何快速查找(三十九)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生从来没有捷径,只有行动才是治疗恐惧和懒惰的唯一良药. 更多原创,欢迎关注:Android…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
