第 361 场 LeetCode 周赛题解
A 统计对称整数的数目
枚举 x x x
class Solution {
public:int countSymmetricIntegers(int low, int high) {int res = 0;for (int i = low; i <= high; i++) {string s = to_string(i);if (s.size() & 1)continue;int s1 = 0, s2 = 0;for (int k = 0; k < s.size(); k++)if (k < s.size() / 2)s1 += s[k] - '0';elses2 += s[k] - '0';if (s1 == s2)res++;}return res;}
};
B 生成特殊数字的最少操作
双指针:则若字符串操作完后为 0 0 0 ,设字符串长为 n n n ,则需要 n n n 或 n − 1 n-1 n−1 (字符串中含
0)操作使得字符串变为 0 0 0 , 若字符串操作完后至少有两位数字,则其最后两位只能是 { 25 , 50 , 75 , 00 } \{25, 50, 75, 00\} {25,50,75,00} 其中之一,枚举可能的后两位,用双指针计算要得到当前枚举值的最少操作数
class Solution {
public:int minimumOperations(string num) {vector<string> tar{"25", "50", "75", "00"};int n = num.size();int res = num.find('0') == num.npos ? n : n - 1;for (auto &s: tar) {int i = s.size() - 1;int j = n - 1;int cur = 0;//得到当前枚举值的最少操作数for (; i >= 0 && j >= 0;) {if (s[i] == num[j]) {i--;j--;} else {j--;cur++;}}if (i < 0)res = min(res, cur);}return res;}
};
C 统计趣味子数组的数目


前缀和:设数组 l i li li 有: l i i = { 1 , n u m s [ i ] % m o d = k 0 , n u m s [ i ] % m o d ≠ k li_i=\left\{\begin{matrix} 1 & , nums[i]\%mod=k \\ 0 & , nums[i]\%mod\ne k \end{matrix}\right. lii={10,nums[i]%mod=k,nums[i]%mod=k,设 l i li li 上的前缀和为 p s i = ( ∑ j = 0 j < i l i i ) % m o d ps_i=(\sum_{j=0}^{j<i} li_i)\%mod psi=(∑j=0j<ilii)%mod ,设子数组 n u m s [ l , r ] nums[l,r] nums[l,r] 为趣味子数组,则有: ( p s r + 1 − p s l ) % m o d = k (ps_{r+1}-ps_{l})\%mod=k (psr+1−psl)%mod=k,即有 p s l = ( ( p s r + 1 − k ) % m o d + m o d ) % m o d ps_l=((ps_{r+1}-k)\%mod+mod)\%mod psl=((psr+1−k)%mod+mod)%mod。
class Solution {
public:using ll = long long;long long countInterestingSubarrays(vector<int> &nums, int modulo, int k) {unordered_map<int, ll> cnt;//cnt[val]: 前缀和val出现的次数cnt[0] = 1;//前缀为空int s = 0;//当前前缀和ll res = 0;for (int i = 0; i < nums.size(); i++) {if (nums[i] % modulo == k)s = (s + 1) % modulo;int s_l = ((s - k) % modulo + modulo) % modulo;res += cnt[s_l];cnt[s]++;}return res;}
};
D 边权重均等查询
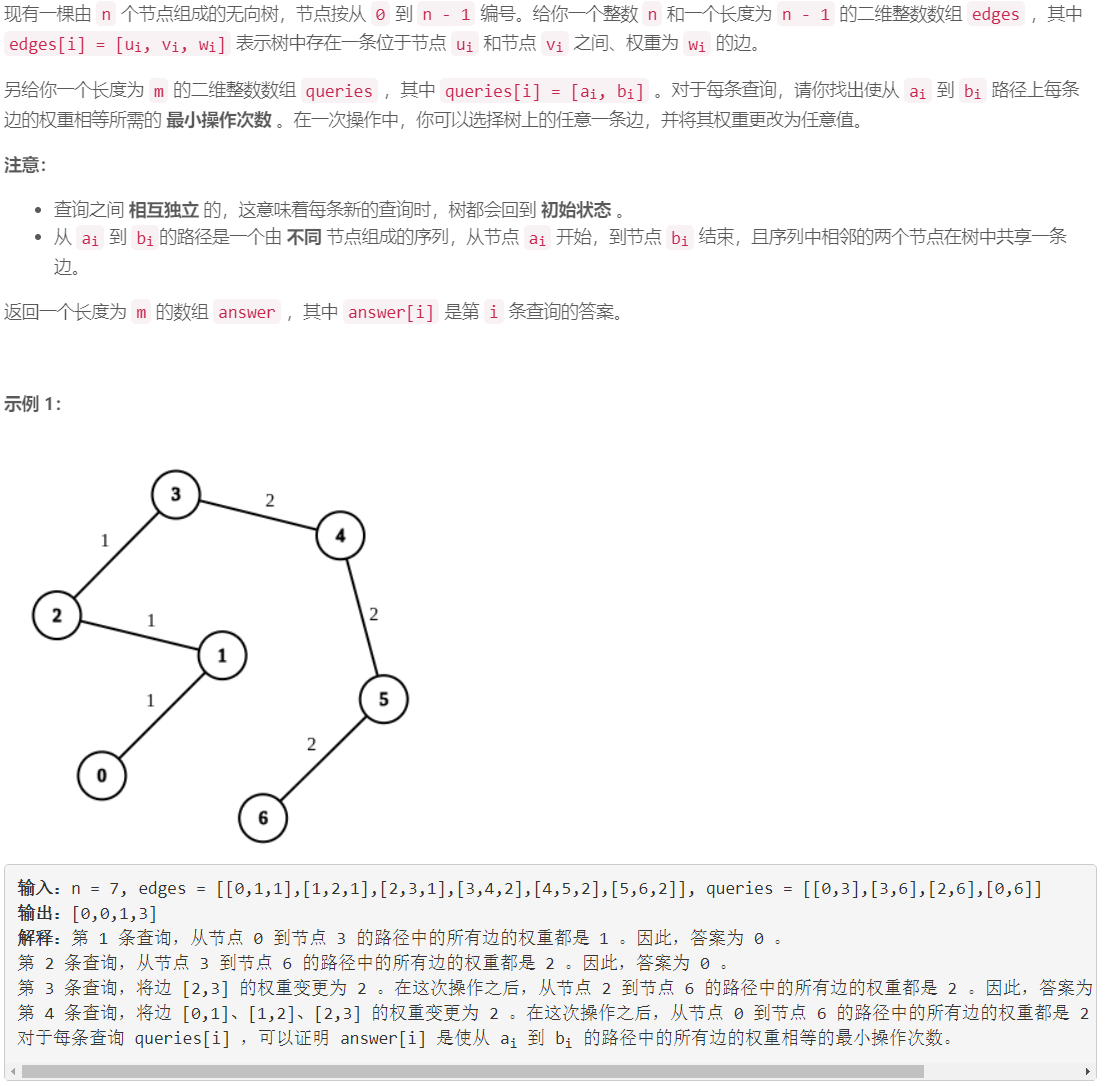
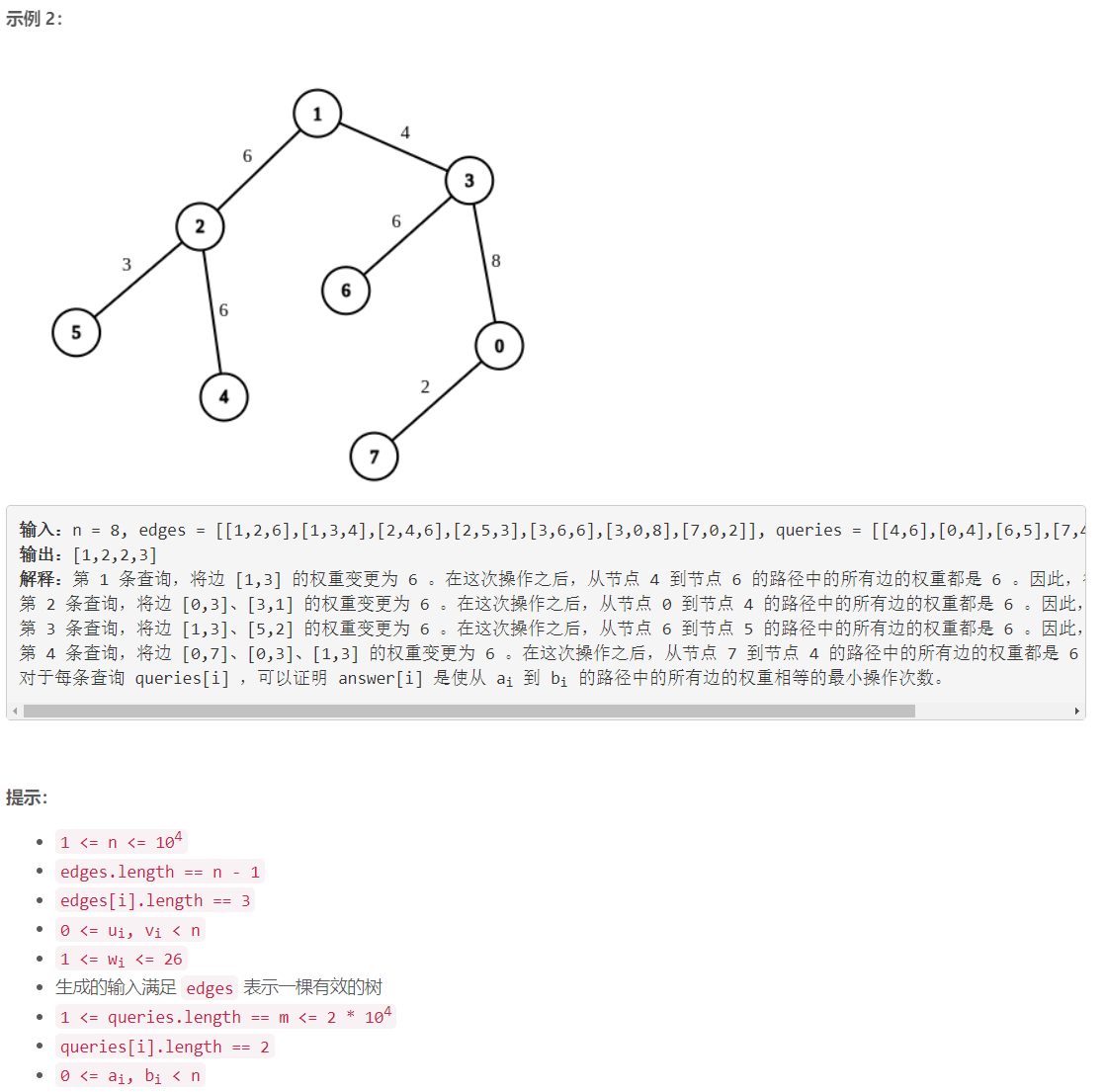
倍增+枚举:1)预处理:设 0 0 0 为树的根节点,枚举边的权重 w _ i d w\_id w_id,从树根开始 d f s dfs dfs ,计算各节点 u u u 到树根的路径上的边数 l e v e l [ u ] level[u] level[u],以及节点 u u u 到树根的路径上边权重为 w _ i d w\_id w_id 的边的数目 s [ u ] [ w _ i d ] s[u][w\_id] s[u][w_id],求倍增数组 p p p: p [ u ] [ j ] p[u][j] p[u][j]为与 u u u 距离为 2 j 2^j 2j的祖先节点。2)对一个查询 ( a , b ) (a,b) (a,b),用倍增的方式求 a a a 和 b b b 的最近公共祖先 c c c ,然后枚举 w _ i d w\_id w_id ,将 a a a 和 b b b 间路径上的边的边权统一为 w _ i d w\_id w_id 的操作数为: ( l e v e l [ a ] − l e v e l [ c ] − ( s [ a ] [ w _ i d ] − s [ c ] [ w _ i d ] ) ) + ( l e v e l [ b ] − l e v e l [ c ] − ( s [ b ] [ w _ i d ] − s [ c ] [ w _ i d ] ) ) \left ( level[a] - level[c] - (s[a][w\_id] - s[c][w\_id]) \right ) + \left ( level[b] - level[c] - (s[b][w\_id] - s[c][w\_id]) \right ) (level[a]−level[c]−(s[a][w_id]−s[c][w_id]))+(level[b]−level[c]−(s[b][w_id]−s[c][w_id]))
class Solution {
public:vector<int> minOperationsQueries(int n, vector<vector<int>> &edges, vector<vector<int>> &queries) {vector<pair<int, int>> e[n];//邻接表int mx_w = 0, mn_w = INT32_MAX;//最大权重、最小权重for (auto &ei: edges) {e[ei[0]].emplace_back(ei[1], ei[2]);e[ei[1]].emplace_back(ei[0], ei[2]);mx_w = max(mx_w, ei[2]);mn_w = min(mn_w, ei[2]);}int level[n], s[n][27];int p[n][15];function<void(int, int, int, int, int)> dfs = [&](int cur, int par, int lev, int sum, int w_id) {if (w_id == mn_w)//倍增数组一轮dfs即可计算for (int i = 0; i < 15; i++)p[cur][i] = i != 0 ? p[p[cur][i - 1]][i - 1] : par;level[cur] = lev;s[cur][w_id] = sum;for (auto &[j, w]: e[cur])if (j != par)dfs(j, cur, lev + 1, w == w_id ? sum + 1 : sum, w_id);};for (int i = mn_w; i <= mx_w; i++)//枚举w_iddfs(0, 0, 0, 0, i);vector<int> res;res.reserve(queries.size());for (auto &qi: queries) {int a = qi[0], b = qi[1];if (a == b) {res.push_back(0);continue;}if (level[a] < level[b])swap(a, b);int c = a;//c最终为a和b的最近公共祖先for (int step = level[a] - level[b], ind = 0; step >= (1 << ind); ind++)if (step >> ind & 1)c = p[c][ind];if (c != b) {int b_ = b;for (int ind = 14; ind >= 0; ind--) {if (p[c][ind] != p[b_][ind]) {c = p[c][ind];b_ = p[b_][ind];}}c = p[c][0];}int res_i = INT32_MAX;for (int w_id = mn_w; w_id <= mx_w; w_id++) {//枚举w_idint t1 = level[a] - level[c] - (s[a][w_id] - s[c][w_id]);int t2 = level[b] - level[c] - (s[b][w_id] - s[c][w_id]);res_i = min(res_i, t1 + t2);}res.push_back(res_i);}return res;}
};
相关文章:

第 361 场 LeetCode 周赛题解
A 统计对称整数的数目 枚举 x x x class Solution { public:int countSymmetricIntegers(int low, int high) {int res 0;for (int i low; i < high; i) {string s to_string(i);if (s.size() & 1)continue;int s1 0, s2 0;for (int k 0; k < s.size(); k)if …...

07-架构2023版-centos+docker部署Canal 实现多端数据同步
canal 工作原理 canal 模拟 MySQL slave 的交互协议,伪装自己为 MySQL slave ,向 MySQL master 发送dump 协议MySQL master 收到 dump 请求,开始推送 binary log 给 slave (即 canal )canal 解析 binary log 对象(原始为 byte 流)基于日志增量订阅和消费的业务包括 数据库镜…...
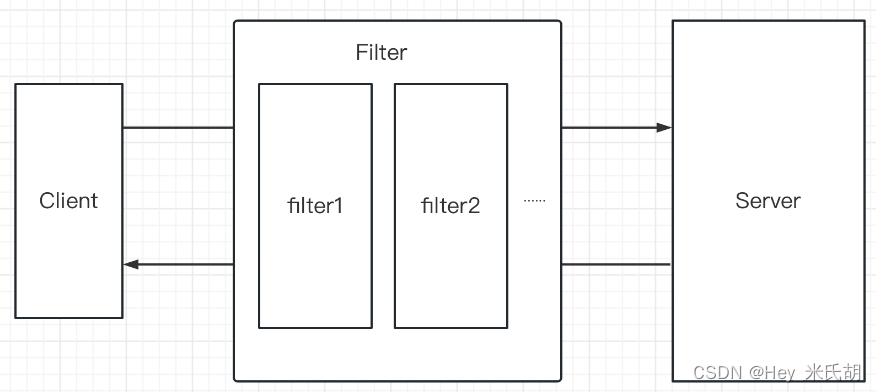
过滤器的应用-Filter
过滤器 1.工作原理 2.创建Filter 2.1通过注解的方式实现 //创建一个类,实现Filter接口 WebFilter(urlPatterns "/myfilter") //urlPatterns表示需要拦截的路径 public class MyFilter implements Filter {Overridepublic void doFilter(ServletReques…...

leetcode236. 二叉树的最近公共祖先(java)
二叉树的最近公共祖先 题目描述递归法代码演示 上期经典 题目描述 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q …...

spacy安装旧版本en_core_web_sm的解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...
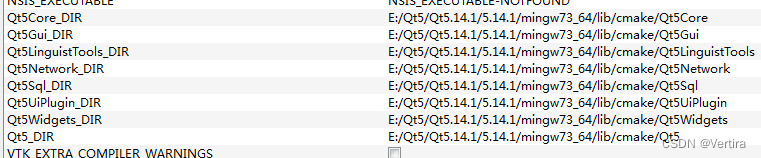
Qt +VTK+Cmake 编译和环境配置(第一篇 采坑)
VTK下载地址:https://vtk.org/download/ cmake下载地址:https://cmake.org/download/ 版本对应方面,如果你的项目对版本没有要求,就不用在意。我就是自己随机搭建的,VTK选择最新版本吧,如果后面其他的库不…...

2023开学礼《乡村振兴战略下传统村落文化旅游设计》许少辉八一新书南宁师范大学图书馆
2023开学礼《乡村振兴战略下传统村落文化旅游设计》许少辉八一新书南宁师范大学图书馆...

C++/C# : C#和C++的不同
C#和C是两种不同的编程语言,虽然在某些方面它们具有相似之处,但它们也有一些明显的不同点,如下: C是一种静态类型编程语言,而C#是一种动态类型编程语言。 C允许开发者手动管理内存的分配和释放,但是C#的垃…...

PCL-直通滤波器原理及实验
文章目录 原理使用过程代码实验总结 原理 直通滤波器的作用是过滤在指定维度方向上取值不在给定值域内的点,即点云数据有xyz三维坐标,选择一个方向的维度的数据,设置一个范围,在这个范围中的点云会被保留,不在此范围内…...
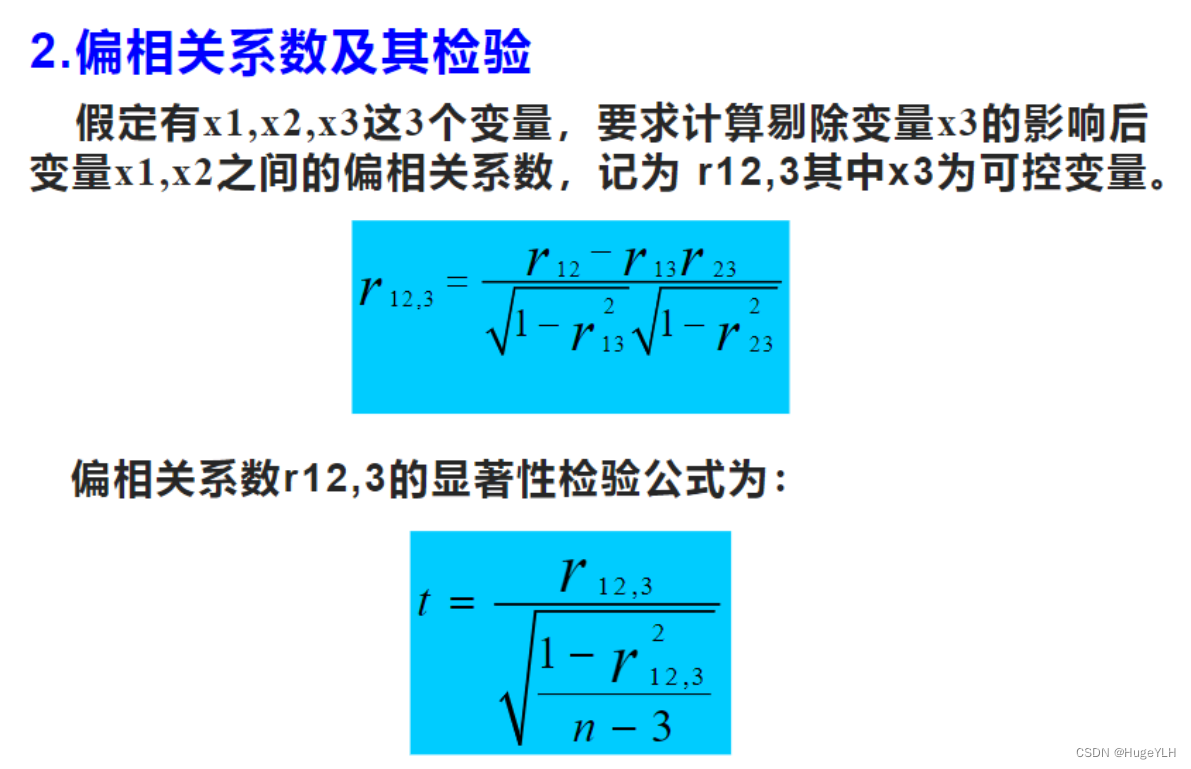
数学建模:相关性分析
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛 数学建模:相关性分析 文章目录 数学建模:相关性分析相关性分析两变量的相关分析PearsonSpearmanKendall tua-b 双变量关系强度测量的指标相关系数的性质代码实现example偏相关分析 相…...
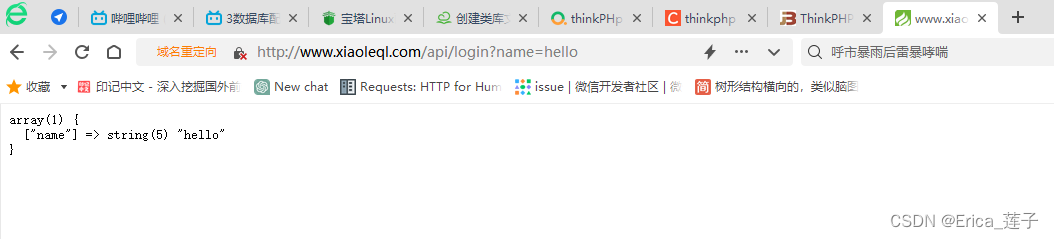
thinkPHP项目搭建
1 宝塔添加站点 (1)打开命令提示行,输入以下命令,找到hosts文件。 for /f %P in (dir %windir%\WinSxS\hosts /b /s) do copy %P %windir%\System32\drivers\etc & echo %P & Notepad %P (2)添加域…...

C++中几种处理函数返回值的方式
目录 C中几种处理函数返回值的方式:值返回引用返回指针返回总结 C中几种处理函数返回值的方式: 值返回 函数可以返回一个具体的值,例如整数、浮点数、结构体、类对象等。返回值被复制到函数调用点,在调用点可以直接使用或赋给其…...

跟我学c++中级篇——c++中的Abominable Function Types
一、Abominable Function Types Abominable Function Types,令人讨厌(憎恶)的函数类型。这个在c的技术点中,很少有人了解。那么什么是Abominable Function Types呢?看下面的例子: using func void(); using func…...
计算机毕设之基于python+django+mysql的影片数据爬取与数据分析(包含源码+文档+部署教程)
影片数据爬取与数据分析分为两个部分,即管理员和用户。该系统是根据用户的实际需求开发的,贴近生活。从管理员处获得的指定账号和密码可用于进入系统和使用相关的系统应用程序。管理员拥有最大的权限,其次是用户。管理员一般负责整个系统的运…...

slog正式版来了:Go日志记录新选择!
在大约一年前,我就写下了《slog:Go官方版结构化日志包[1]》一文,文中介绍了Go团队正在设计并计划在下一个Go版本中落地的Go官方结构化日志包:slog[2]。但slog并未如预期在Go 1.20版本[3]中落地,而是在golang.org/x/exp…...
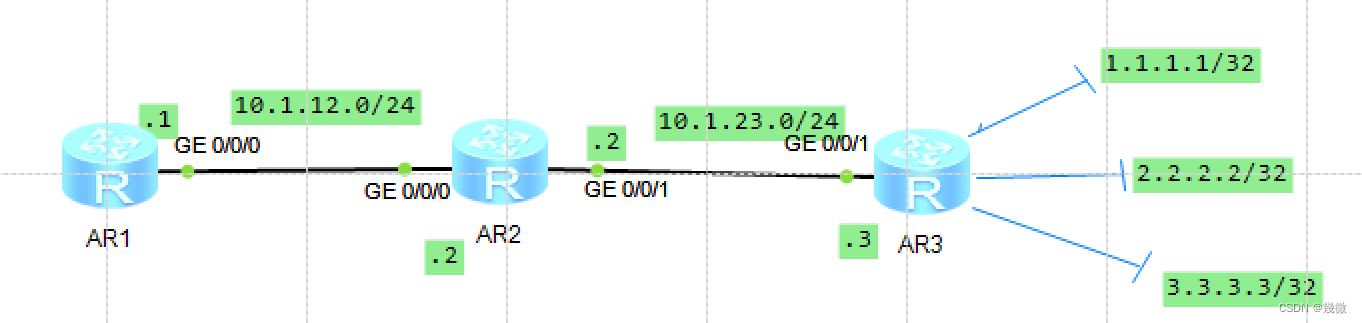
华为静态路由配置实验(超详细讲解+详细命令行)
系列文章目录 华为数通学习(7) 前言 一,静态路由配置 二,网络地址配置 AR1的配置: AR2的配置: AR3的配置: 三,测试是否连通 AR1的配置: 讲解: AR2的配置&#…...

axios源码学习
1 判断一个对象是否普通对象 Symbol.toStringTag:可以修改Object.prototype.toString.call返回的后缀,普通对象自带该属性,不需要设置,如果设置说明该对象不是普通对象Symbol.iterator:拥有该属性的对象可以使用for o…...

【SpingBoot】详细介绍SpringBoot项目中前端请求到数据库再返回前端的完整数据流转,并用代码实现
在SpringBoot项目中,前端请求到最终返回的完整数据流转一般包括以下几个步骤: 前端发送HTTP请求到后端Controller。 Controller接收到请求后,调用相关Service处理业务逻辑。 Service调用DAO层获取数据。 DAO层访问数据库获取数据。 数据库…...

kubesphere devops使用
一、创建项目 1 创建项目 企业管理员切换到相应企业空间(租户),创建项目,k8s集群会创建一个相同名字的namespace。如下图所示管理员创建一个ipaas-devops项目。 2.创建镜像拉取密钥信息 进入项目如ipaas-devops,选择配置->保密字典->创建…...

Selenium如何用于编写自动化测试脚本?
Selenium如何用于编写自动化测试脚本?它提供了许多测试工具和API,可以与浏览器交互,模拟用户操作,检查网页的各个方面。下面是一些步骤,可以帮助你编写Selenium自动化测试脚本。 1、安装Selenium库和浏览器驱动程序 首…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...
