论文阅读_变分自编码器_VAE
英文名称: Auto-Encoding Variational Bayes
中文名称: 自编码变分贝叶斯
论文地址: http://arxiv.org/abs/1312.6114
时间: 2013
作者: Diederik P. Kingma, 阿姆斯特丹大学
引用量: 24840
1 读后感
VAE 变分自编码(Variational Autoencoder)是一种生成模型,它结合了自编码器和概率图模型的思想。它的目标是:解决对复杂性高,且量大的数据难以拟合的问题。具体方法是:使用基于变分推理的原理,以变分下界作为目标函数,用梯度方法求取模型参数。
2 通俗理解

听起来非常抽象,简单地说:变分自编码器是自编码器的改进版。
2.1 自编码器
自编码器通常由编码器和解码器两部分组成,其中编码器将原始数据映射到低维表示,解码器则将低维表示映射回原始数据空间。即:原始数据为x,将其输入编码器降维后,变成数据z,再经过编码器还原成数据 x’。它常用于高维数据的低维表示和从低维表示中生成高维数据。比如:图像去噪,修复图片,生成高分辨率图片等。
2.2 变分自编码器
变分自编码器在中间加了一层逻辑,它假设中间过程的数据 z 每个维度都是正态分布的,可以使用:均值 μ 和 方差 σ 表示。由此,就变成了变分自编码器:训练编码器和解码器网络,可将图片x分布压缩后再拆分成多个高斯分布的叠加,如上图所示。
3 相关概念
3.1 高斯分布
使用高斯分布的原因是:每张训练图片的内容都不一样,训练过程中产生的潜空间z也是离散的,不能确定它的分布。比如数据有满月和半月,但无法产生2/3月亮。而高斯分布是连续的,如果能把中间的表征z用正态分布描述,它就是平滑的,理论上就可以产生介于两图之间的内容图片,它具有一定的潜在空间的连续性和插值性质。
3.2 高斯混合模型 GMM

可以想见,z的分布相当复杂,不是一个简单的高斯分布可以描述的。图中红色为分布曲线。它可分解为一系列不同频率、不同振幅、不同相位的正弦波。也就是说可以用多个正态分布(高斯分布)的叠加去逼近任意一个分布。可以说 VAE 是对 GMM 方法的改进版。
3.3 KL散度
用于衡量两个分布之间的距离。
3.4 最大似然估计
似然与概率类似,但有如下区别:给定一个函数 P ( x ∣ θ ) P(x|\theta) P(x∣θ) ,x是样本点, θ \theta θ是参数。
(1)当 θ \theta θ 为常量, x为变量时,称 P 为关于 x 的概率函数;
(2)当 x 为常量, θ \theta θ 为变量时,称 P 为关于 θ \theta θ 的似然函数;
求解最大似然是指:求使得样本点 x 能够以最大概率发生的 θ \theta θ 的取值。
3.5 变分推断
变分 Variational 是通过引入一个简化的参数化分布来近似复杂的后验分布。这个参数化分布被称为变分分布,它属于一种可计算的分布族。通过调整变分分布的参数,使其尽可能接近真实的后验分布,从而实现近似推断。
3.6 变分下界
变分下界(variational lower bound)通常用于衡量变分分布与真实后验分布之间的差异。
E L B O = E [ l o g p ( x , z ) − l o g q ( z ) ] ELBO = E[log\ p(x, z) - log\ q(z)] ELBO=E[log p(x,z)−log q(z)]
其中,ELBO 代表变分下界(Evidence Lower BOund),x代表观测数据,z代表未知变量,p(x, z)表示真实的联合分布,q(z)表示变分分布。
3.7 代入本文中场景
有一张图 x(后验分布),想把它映射成 z,假设 z 是混合高斯分布(先验分布),各维可能描述颜色,材质……,用函数函数 g() 把 x 分解成高斯分布,它的逆过程是用 f() 根据高斯分布还原原始图 x‘ ,最终恢复的图片 x’=f(g(x)),目标是想让 x’-x 值尽量小,就是说:图 x 转成潜空间 z 再转回原始图 x’,图像最好没变化。
综上所述,无论x是什么,通过变换,产生的x’都与x很像,中间过程的 z 还能用高斯参数表示,求这样的函数f和g的神经网络。
3.8 蒙特卡洛估计
蒙特卡洛估计(Monte Carlo estimation)是一种基于随机抽样的统计估计方法,用于计算复杂问题的数值近似解。其基本思想是通过生成大量的随机样本,利用这些样本的统计特性来估计问题的解。
4 方法
(以下图和公式中的变量含义重新开始定义,不要与上面混淆)

先看一下论文主图,N是数据集,x是真实空间(可观察),z是潜空间(不可观察的连续空间);实线表示生成模型 pθ(z)pθ(x|z),虚线表示p的变分近似 qφ(z|x)(也称识别模型),文中使用的方法是用 qφ(z|x) 模拟难以计算的 pθ(z|x),变分参数 φ 与生成模型参数 θ 一起学习。这里的q可视为编码器,而p视为解码器。
4.1 变分边界
边界似然(Marginal Likelihood)是各观测数据点(每张图片)在给定模型下的概率之和(原图的概率),值越大模型越好,它描述的是图像重建的好不好(重建损失)。
l o g p θ ( x ( 1 ) , ⋅ ⋅ ⋅ , x ( N ) ) = ∑ i = 1 N l o g p θ ( x ( i ) ) log\ p_θ(x^{(1)}, · · · , x^{(N)}) = \sum^N_{i=1} log\ p_θ(x^{(i)}) log pθ(x(1),⋅⋅⋅,x(N))=i=1∑Nlog pθ(x(i))
各数据点的概率:
l o g p θ ( x ( i ) ) = D K L ( q φ ( z ∣ x ( i ) ) ∣ ∣ p θ ( z ∣ x ( i ) ) ) + L ( θ , φ ; x ( i ) ) log\ p_θ(x(i)) = D_{KL}(q_φ(z|x^{(i)})||p_θ(z|x^{(i))}) + L(θ, φ; x^{(i)}) log pθ(x(i))=DKL(qφ(z∣x(i))∣∣pθ(z∣x(i)))+L(θ,φ;x(i))
前半部分 DKL 是z的模拟值和真实后验的 KL 散度,KL 散度一定大于0,后半部分 L 是变分下界(建模的目标):
log p θ ( x ( i ) ) ≥ L ( θ , ϕ ; x ( i ) ) = E q ϕ ( z ∣ x ) [ − log q ϕ ( z ∣ x ) + log p θ ( x , z ) ] \log p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)}\right) \geq \mathcal{L}\left(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{x}^{(i)}\right)=\mathbb{E}_{q_{\boldsymbol{\phi}}(\mathbf{z} \mid \mathbf{x})}\left[-\log q_{\boldsymbol{\phi}}(\mathbf{z} \mid \mathbf{x})+\log p_{\boldsymbol{\theta}}(\mathbf{x}, \mathbf{z})\right] logpθ(x(i))≥L(θ,ϕ;x(i))=Eqϕ(z∣x)[−logqϕ(z∣x)+logpθ(x,z)]
这里的E是期望,右测是变分下界 ELBO 的公式。
通过移项得到了变分下界的目标函数,公式如下:
L ( θ , ϕ ; x ( i ) ) = − D K L ( q ϕ ( z ∣ x ( i ) ) ∥ p θ ( z ) ) + E q ϕ ( z ∣ x ( i ) ) [ log p θ ( x ( i ) ∣ z ) ] \mathcal{L}\left(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{x}^{(i)}\right)=-D_{K L}\left(q_{\boldsymbol{\phi}}\left(\mathbf{z} \mid \mathbf{x}^{(i)}\right) \| p_{\boldsymbol{\theta}}(\mathbf{z})\right)+\mathbb{E}_{q_{\boldsymbol{\phi}}\left(\mathbf{z} \mid \mathbf{x}^{(i)}\right)}\left[\log p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)} \mid \mathbf{z}\right)\right] L(θ,ϕ;x(i))=−DKL(qϕ(z∣x(i))∥pθ(z))+Eqϕ(z∣x(i))[logpθ(x(i)∣z)]
目标函数是最大化变分下界(Variational Lower Bound):第一项 KL散度(Kullback-Leibler Divergence)衡量了潜在变量的分布与先验分布之间的差异(z的差异:越小越好),第二项 重建损失(Reconstruction Loss)衡量了重建样本与原始样本之间相似度(x为原图的概率:越大越好),所以整体 L 越大越好。
z 对应的多个高斯分布的均值和方差都不是固定的值,它们通过神经网络计算得来,神经网络的参数通过训练得到。
4.2 具体实现
这里引入了噪声变量e作为辅助变量,来实现 q 的功能。
z ~ = g ϕ ( ϵ , x ) \widetilde{z}=g_\phi(\epsilon,x) z =gϕ(ϵ,x)
对某个函数 f(z) 的期望进行蒙特卡洛估计,具体通过采样实现,其minibatch 是从有N个数据点的数据集中,随机抽取M个点:
L ( θ , ϕ ; X ) ≃ L ~ M ( θ , ϕ ; X M ) = N M ∑ i = 1 M L ~ ( θ , ϕ ; x ( i ) ) \mathcal{L}(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{X}) \simeq \widetilde{\mathcal{L}}^{M}\left(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{X}^{M}\right)=\frac{N}{M} \sum_{i=1}^{M} \widetilde{\mathcal{L}}\left(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{x}^{(i)}\right) L(θ,ϕ;X)≃L M(θ,ϕ;XM)=MNi=1∑ML (θ,ϕ;x(i))
可以将KL散度看成限制参数φ的正则化项。而重建误差部分:先用函数 gφ(.) 将数据点 x 和随机噪声向量映射到该数据点的近似后验样本z,然后计算 log pθ(x(i)|z(i,l)),等于生成模型下数据点 x(i) 的概率密度,从而计算重建误差。
4.3 变分自编码器
在变分自编码器的场景中,先验是中心各向同性的多元高斯分布:
log q ϕ ( z ∣ x ( i ) ) = log N ( z ; μ ( i ) , σ 2 ( i ) I ) \log q_{\boldsymbol{\phi}}\left(\mathbf{z} \mid \mathbf{x}^{(i)}\right)=\log \mathcal{N}\left(\mathbf{z} ; \boldsymbol{\mu}^{(i)}, \boldsymbol{\sigma}^{2(i)} \mathbf{I}\right) logqϕ(z∣x(i))=logN(z;μ(i),σ2(i)I)
其中均值和标准差是编码 MLP 的输出。由于是高斯分布:
z ( i , l ) = g ϕ ( x ( i ) , ϵ ( l ) ) = μ ( i ) + σ ( i ) ⊙ ϵ ( l ) z^{(i,l)} = g_\phi(x^{(i)}, \epsilon^{(l)}) = μ^{(i)} + σ^{(i)} \odot \epsilon^{(l)} z(i,l)=gϕ(x(i),ϵ(l))=μ(i)+σ(i)⊙ϵ(l)
引入高斯分布的KL散度,最终目标函数是:
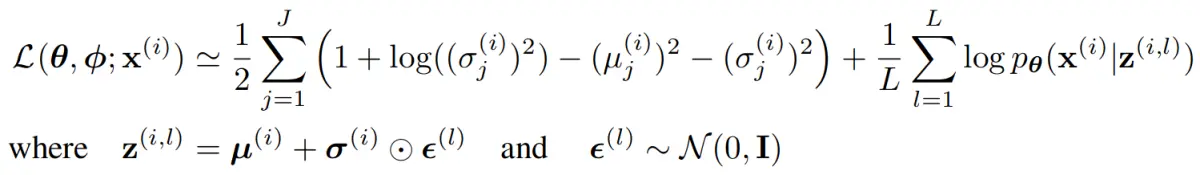
相关文章:
论文阅读_变分自编码器_VAE
英文名称: Auto-Encoding Variational Bayes 中文名称: 自编码变分贝叶斯 论文地址: http://arxiv.org/abs/1312.6114 时间: 2013 作者: Diederik P. Kingma, 阿姆斯特丹大学 引用量: 24840 1 读后感 VAE 变分自编码(Variational Autoencoder)是一种生…...
springboot整合elasticsearch使用案例
引入依赖 <dependency><groupId>org.elasticsearch.client</groupId><artifactId>elasticsearch-rest-high-level-client</artifactId> </dependency> 添加注入 import org.apache.http.HttpHost; import org.elasticsearch.client.Res…...

Unity制作下雨中的地面效果
Unity引擎制作下雨效果 大家好,我是阿赵。 之前介绍了Unity引擎里面通过UV偏移做序列帧动画的做法,这里再介绍一个进阶的用法,模拟地面下雨的雨点效果。 一、原理 最基本的原理,还是基于这个序列帧动画的做法。不过这里做一点…...

windows从0搭建python3开发环境与开发工具
文章目录 一、python3下载安装1、下载2、安装3、测试 二、安装VS Code1、安装2、安装python插件3、测试 三、pip命令的使用1、基本命令2、修改pip下载源 一、python3下载安装 1、下载 打开 WEB 浏览器访问 https://www.python.org/downloads/windows/ ,一般就下载…...

centos中得一些命令 记录
redis命令 链接redis数据库的命令 redis-cli如果 Redis 服务器在不同的主机或端口上运行,你需要提供相应的主机和端口信息。例如: redis-cli -h <hostname> -p <port>连接成功后,你将看到一个类似于以下的提示符,表…...
Python实现Word、Excel、PPT批量转为PDF
今天看见了一个有意思的脚本Python批量实现Word、EXCLE、PPT转PDF文件。 因为我平时word用的比较的多,所以深有体会,具体怎么实现的我们就不讨论了,因为这个去学了也没什么提升,不然也不会当作脚本了。这里我将其放入了pyzjr库中…...

LLM大模型推理加速 vLLM
参考: https://github.com/vllm-project/vllm https://zhuanlan.zhihu.com/p/645732302 https://vllm.readthedocs.io/en/latest/getting_started/quickstart.html ##文档 加速原理: PagedAttention,主要是利用kv缓存 使用: #…...

Python|小游戏之猫捉老鼠!!!
最近闲(mang)来(dao)无(fei)事(qi),喜欢研究一些小游戏,本篇文章我主要介绍使用 turtle 写的一个很简单的猫捉老鼠的小游戏,主要是通过鼠标控制老鼠(Tom)的移动,躲避通过电脑控制的猫(Jerry)的追捕。 游戏主体思考逻辑࿱…...
万里路,咫尺间:汽车与芯片的智能之遇
目前阶段,汽车产业有两个最闪耀的关键词,就是智能与低碳。 在践行双碳目标与产业智能化的大背景下,汽车已经成为了能源技术、交通技术、先进制造以及通信、数字化、智能化技术的融合体。汽车的产品形态与产业生态都在发生着前所未有的巨大变革…...
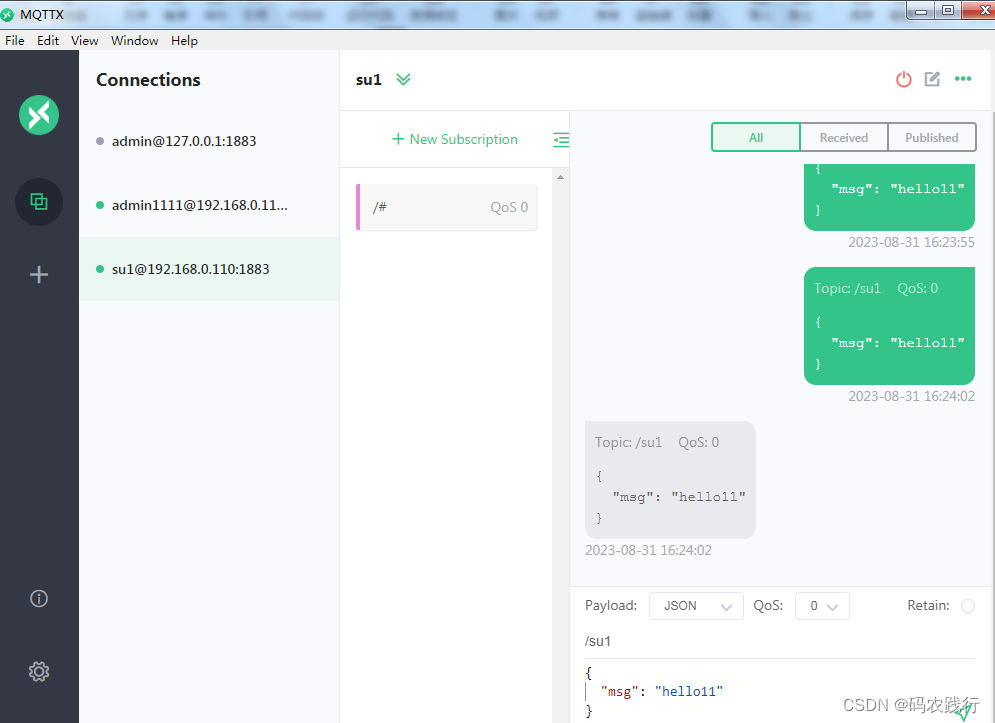
Ubuntu22.04.1上 mosquitto安装及mosquitto-auth-plug 认证插件配置
Ubuntu22.04.1上 mosquitto安装及mosquitto-auth-plug 认证插件配置 1、先上效果,可以根据mysql中mosquitto数据库的不同users角色登陆mosquitto: SELECT * FROM mosquitto.users; id,username,pw,super 1,jjolie,PBKDF2$sha256$901$yZnELWKK4NnaNNJl…...
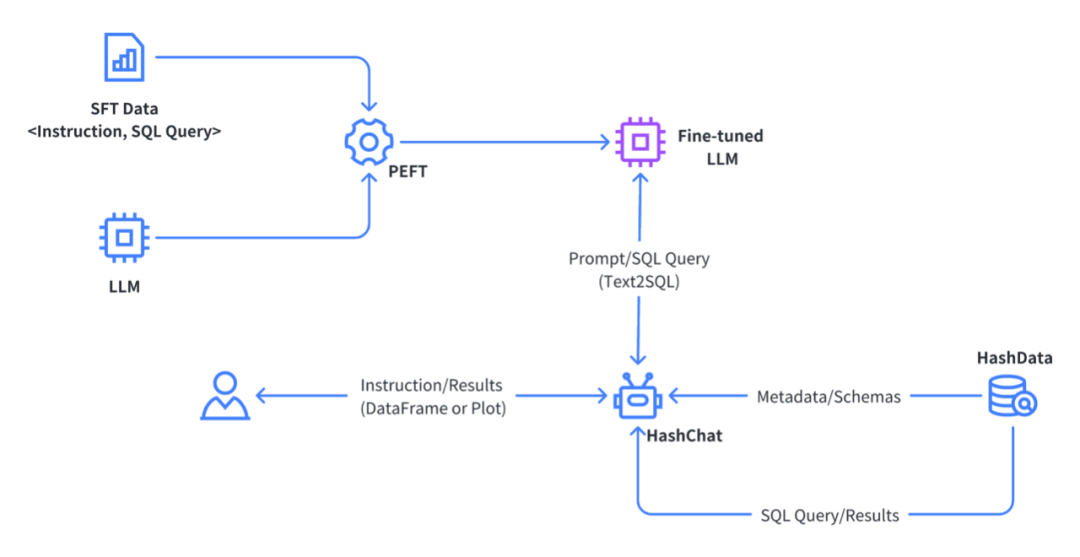
CCKS2023:基于企业数仓和大语言模型构建面向场景的智能应用
8月24日-27日,第十七届全国知识图谱与语义计算大会(CCKS 2023)在沈阳召开。大会以“知识图谱赋能通用AI”为主题,探讨知识图谱对通用AI技术的支撑能力,探索知识图谱在跨平台、跨领域等AI任务中的作用和应用途径。 作为…...

LeetCode 热题 100——无重复字符的最长子串(滑动窗口)
题目链接 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 题目解析 从s字符串中,去找出连续的子串,使该子串中没有重复字符,返回它的最长长度。 暴力枚举 依次以第一个、第二个、第三个等等为起点去遍历字符串&a…...
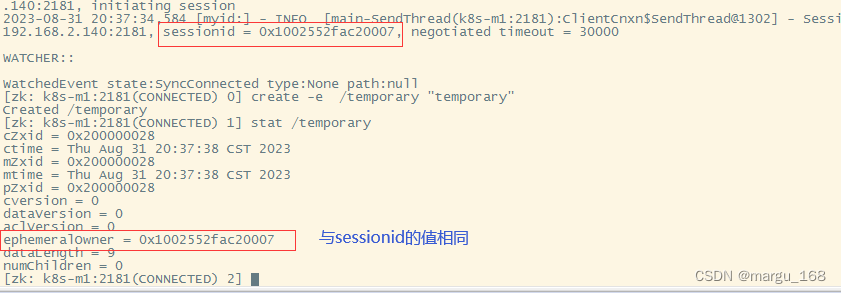
【zookeeper】zookeeper的shell操作
Zookeeper的shell操作 本章节将分享一些zookeeper客服端的一些命令,实验操作有助于理解zookeeper的数据结构。 Zookeeper命令工具 在前一章的基础上,在启动Zookeeper服务之后,输入以下命令,连接到Zookeeper服务。连接成功之后&…...
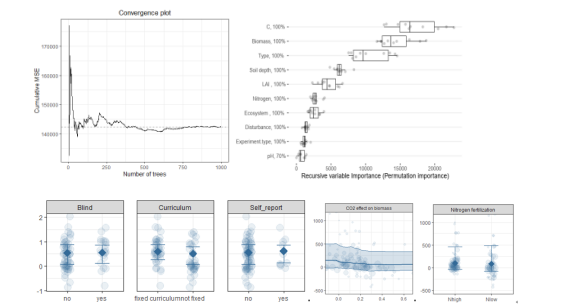
R语言Meta分析核心技术
Meta分析是针对某一科研问题,根据明确的搜索策略、选择筛选文献标准、采用严格的评价方法,对来源不同的研究成果进行收集、合并及定量统计分析的方法,最早出现于“循证医学”,现已广泛应用于农林生态,资源环境等方面。…...

Oracle数据库尚硅谷学习笔记
文章目录 Oracle数据库体系结构简介补充SQL初步导入sql文件别名连接符distinct去重的坑 过滤和排序数据日期格式比较运算其它比较运算符逻辑运算优先级排序 单行函数SQL中不同类型的函数单行函数字符数值日期转换通用 使用条件表达式嵌套查询 多表查询等值连接非等值连接左外连…...

CG MAGIC进行实体渲染后!分析渲染器CR和VR的区别之处!
新手小白来说,如何选择渲染器,都会提出疑问? 渲染效果图究竟用CR渲染器还是VR渲染器呢? 今天,CG MAGIC小编通过一个真实的项目场景,实例渲染之后,CR渲染器和VR渲染器区别有哪几点? 1…...

Ubuntu下Python3与Python2相互切换
参考文章:https://blog.csdn.net/Nicolas_shen/article/details/124144931 设置优先级 sudo update-alternatives --install /usr/bin/python python /usr/bin/python2 100 sudo update-alternatives --install /usr/bin/python python /usr/bin/python3 200...

【深度学习】实验07 使用TensorFlow完成逻辑回归
文章目录 使用TensorFlow完成逻辑回归1. 环境设定2. 数据读取3. 准备好placeholder4. 准备好参数/权重5. 计算多分类softmax的loss function6. 准备好optimizer7. 在session里执行graph里定义的运算 附:系列文章 使用TensorFlow完成逻辑回归 TensorFlow是一种开源的…...

2023-09-04 Linux 让shell编译脚本里面设置的环境变量改变kernel里面驱动文件的宏定义值方法,我这里用来做修改固件版本
一、原生的读取版本接口是/proc/version,我这里需要提供获取固件版本号的api给app,因为版本号会经常需要修改,如果每次都到kernel下修改比较麻烦,我这里是想在编译脚本里面对版本号进行修改,这样方便一点。 二、主要修…...

Python操作Excel实战:Excel行转列
# 1、原始数据准备 样例数据准备 地区1m2-5m6-10m11-20m21-40m地区单价计费单位费用最小值费用最大值北京13012011010090 天津13012011010090 石家庄13012011010090 保定140130120110100 张家口170150130120110 邢台1401201101…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...
