罗马数字转整数
罗马数字转整数
题目:
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000例如, 罗马数字 2 写做 II ,即为两个并列的 1 。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:I 可以放在 V (5) 和 X (10) 的左边,来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边,来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边,来表示 400 和 900。
给定一个罗马数字,将其转换成整数。示例 1:
输入: s = "III"
输出: 3示例 2:
输入: s = "IV"
输出: 4示例 3:
输入: s = "IX"
输出: 9示例 4:
输入: s = "LVIII"
输出: 58
解释: L = 50, V= 5, III = 3.示例 5:
输入: s = "MCMXCIV"
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.
解题思路1: 直接代码模拟
class Solution {public int romanToInt(String s) {char[] ch = s.toCharArray();int ans = 0;for(int i = 0; i < ch.length; i++) {char c = ch[i];if(c == 'I') {if(i + 1 < ch.length && ch[i + 1] == 'V') {ans += 4;} else if(i + 1 < ch.length && ch[i + 1] == 'X') {ans += 9;} else {ans += 1;}} else if(c == 'V') {if(i > 0 && ch[i - 1] == 'I') {} else {ans += 5;}} else if(c == 'X') {if(i > 0 && ch[i - 1] == 'I') {} else if(i + 1 < ch.length && ch[i + 1] == 'L') {ans += 40;} else if(i + 1 < ch.length && ch[i + 1] == 'C') {ans += 90;} else {ans += 10;}} else if(c == 'L') {if(i > 0 && ch[i - 1] == 'X') {} else {ans += 50;}} else if(c == 'C') {if(i > 0 && ch[i - 1] == 'X') {} else if(i + 1 < ch.length && ch[i + 1] == 'D') {ans += 400;} else if(i + 1 < ch.length && ch[i + 1] == 'M') {ans += 900;} else {ans += 100;}} else if(c == 'D') {if(i > 0 && ch[i - 1] == 'C') {} else {ans += 500;}} else {if(i > 0 && ch[i - 1] == 'C') {} else {ans += 1000;}}}return ans;}
}
解题思路2: 如果小的数字在大的数字的右边,那么可以将每个字符视作一个单独的值,累加每个字符对应的数值,如果一个数字右侧的数字比它大,则将该数字的符号取反
class Solution {private static Map<Character, Integer> symbolValues = new HashMap<Character, Integer>() {{put('I', 1);put('V', 5);put('X', 10);put('L', 50);put('C', 100);put('D', 500);put('M', 1000);}};public int romanToInt(String s) {int ans = 0;int n = s.length();for (int i = 0; i < n; ++i) {int value = symbolValues.get(s.charAt(i));if (i < n - 1 && value < symbolValues.get(s.charAt(i + 1))) {ans -= value;} else {ans += value;}}return ans;}
}
相关文章:

罗马数字转整数
罗马数字转整数 题目: 罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M …...
processflow流程图多人协作预热
前言 在线上办公如火如荼的今天,多人协作功能是每个应用绕不开的门槛。processflow在线流程图(前身基于drawio二次开发)沉寂两年之久,经过长时间设计开发,调整,最终完成了多人协作的核心模块设计。废话不多…...
)
PCL点云处理之快速计算多个点到同一直线的距离(二百零五)
PCL点云处理之快速计算多个点到同一直线的距离(二百零五) 一、算法简介二、具体实现1.代码2.结果一、算法简介 点到直线的距离计算,是一种常用的算法,在点云处理中,经常遇到需要计算多个点云到同一条直线的距离计算需求,此时若是逐点计算将耗费大量的时间,熟悉点到直线…...

xxl-job 任务调度搭建及简单使用
xxl-job是开源架构,可以通过它实现调度中心和执行器。 git地址和 官网中进行了详细的技术说明。 xxl-job支持单机部署和集群式部署,在集群式部署中又可以实现调度中心集群式部署和执行器集群式部署。本文主要针对调度中心和执行器分离单机部署方式进…...
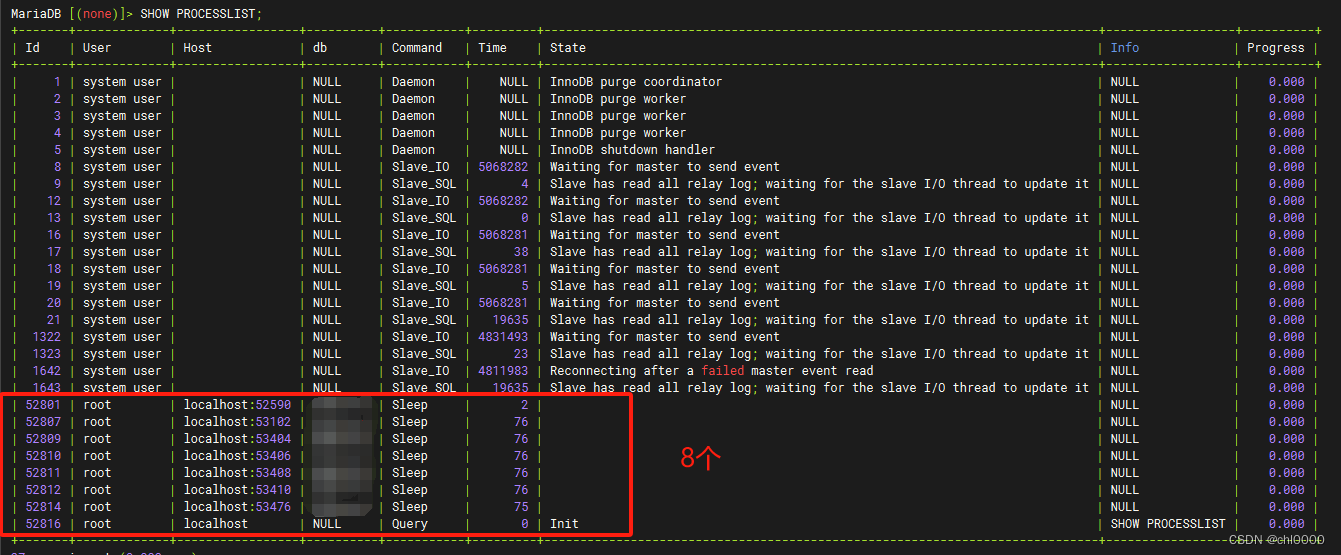
mysql数据库使用技巧整理
查看当前数据库已建立的client连接 > SHOW VARIABLES LIKE max_connections; -- 查看数据库允许的最大连接数,不是实时正在使用的连接数 > SHOW STATUS LIKE Threads_connected; -- 查看当前数据库client的连接数 > SHOW PROCESSLIST; -- 查看具体的连接...

车规微控制器的ECC机制及EMU外设
车规微控制器的ECC机制及EMU外设 文章目录 车规微控制器的ECC机制及EMU外设引言ECC的基本原理ECC RAM的访问方式ECC RAM的初始化SRAM ECC错误注入及EMU外设Flash ECC校验参考文献 引言 ECC是微控制器系统中,用于保障信息安全的常用机制,主要是避免存储设…...

Less的强大变量用法
less中的变量应用十分强大,可以灵活的应用到各种不同需求的场景。 一,属性值变量 声明:sass声明变量是用$符号,而less声明变量是用符号 作用域:也区分为全局变量和局部变量,如果引用的变量有定义局部变量&…...

【相机标定】opencv python 标定相机内参时不计算 k3 畸变参数
文章目录 1. 背景2. 完整的 opencv python 标定相机内参过程3. 选择是否计算畸变参数 k3 1. 背景 畸变参数 k3 通常用于描述径向畸变的更高阶效应,即在需要高精度的应用中可以用到,一般的应用中 k1, k2 足矣。 常见的应用中, orbslam3 中是否…...
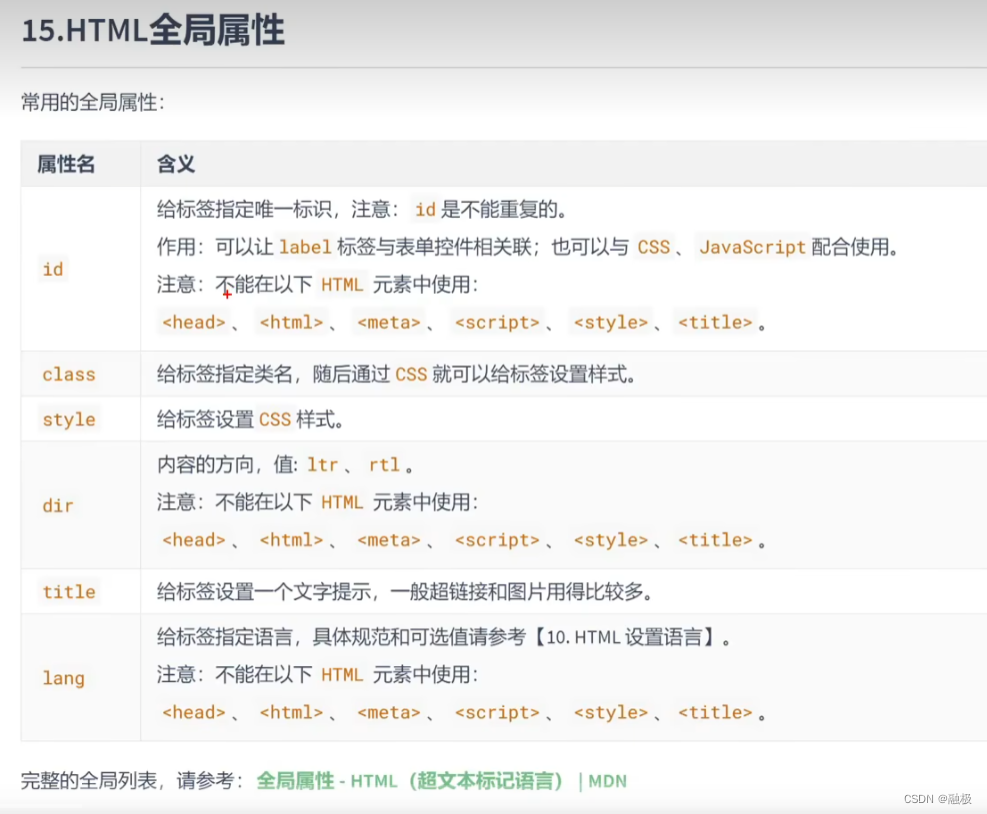
html 标签简介
概述 标签的效果不重要,重要的是标签的语义。 文本标签 文本标签用于包裹:词汇、短语等。排版标签,比如div,p,h1等。排版标签更宏观(大段的文字),文本标签更微观(词汇、短语)。文…...

dos汇编总结
前言: 计组课本需要学习汇编,可惜自己看不太懂。这里发现一个学习方法交给大家。其实新手可能一些抽象表示难理解,这里我把我学习的疑问点以及思路记录一下。 要点: 这里我以题为例给大家分析 输出输入对应大写字母的小写字母 …...

四川玖璨电子商务有限公司:短视频有什么运营
根据短视频有什么运营,短视频的拍摄工具多种多样。无论是在手机上拍摄还是使用专业摄影设备,拍摄短视频的目的都是为了吸引观众的注意力和提升内容的质量。从小花费到高投入,在不断发展的短视频行业中,拍摄方法也得到了不断创新和…...
混合查询多家快递,快速掌握物流信息
在现代社会,快递服务已成为我们日常生活的重要组成部分。无论是购物还是文件传递,我们都需要快递服务的帮助。然而,不同的快递公司需要不同的查询方法,这无疑增加了我们的查询难度。因此,有没有一种方法可以让我们一次…...

独立站新手引流,谷歌SEO工具汇总
俗话说“工欲善其事,必先利其器”,做谷歌SEO也一样,要想做好并提升SEO效果,卖家就需要了解并利用好SEO工具。那我们今天就来盘点一下,常用的SEO工具有哪些吧~ 网站检测工具 1、PageSpeed Insights:这是谷…...

SpringMvc 与 Lombok 碰撞导致 JSON 反序列化失败
SpringMvc 与 Lombok 中 JSON 反序列化失败 错误复现_1 Data public class User{private Long id;private boolean isOk; }RequestMapping public R<User> getUser(RequestBody User user){return R.success(user); }// 前端传参 - {"id": 123456789,"i…...

怎么样显卡叠加,什么是NVIDIA 显卡 非公、公版、涡轮卡
1、显存叠加的问题,因为这个跟是否是深度学习无关: 先说一下显存叠加的问题,因为这个跟是否是深度学习无关:一台机器有多张显卡,显存不会叠加!显卡里面包含了显存、cache、计算单元、通信等,每…...

CentOS安装Elasticsearch集群
前言 之前使用的ES集群是其他公司维护,没有机会安装,后来做其他项目,终于有机会安装ES集群,简单记录一下备用 一、安装jdk 安装jdk1.8就可以,可以参考另一篇文章,这里就不细说了 二、修改系统参数 如果在…...

计算机专业毕业生指南
在大四毕业时,完成计算机毕业设计需要一定的计划和组织。以下是一些建议,帮助你在三个月内快速完成毕业设计: 选择一个合适的主题: 选择一个你感兴趣的主题,这将激发你的热情,使你更有动力完成项目。 确保…...

Springboot集成Docker并将镜像推送linux服务器
案例使用springboot项目,在IDEA 中集成Docker生成镜像,并将镜像发布到linux服务器 具体步骤如下: 1、Centos7安装Docker 更新系统的软件包列表 sudo yum update安装Docker所需的软件包和依赖项: sudo yum install docker完成…...
数字孪生与GIS:智慧城市的未来之路
数字孪生和地理信息系统(GIS)是两个在现代科技中崭露头角的概念,它们的融合为智慧城市项目带来了革命性的机会。本文将解释数字孪生为何需要融合GIS,并以智慧城市项目为例进行说明。 数字孪生是一种虚拟模型,它精确地…...

nas汇编程序的调试排错方法
nas汇编程序的调试排错方法: 1、查找是哪一步错了 2、查看对应的*.lst文件,本例中是"asmhead.lst" 3、根据*.lst文件的[ERROR #002]提示查看源码,改错。 4、重新运行编译,OK 1、查找是哪一步错了: nask.ex…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...
