【数据结构】二叉搜索树——二叉搜索树的概念和介绍、二叉搜索树的简单实现、二叉搜索树的增删查改

二叉搜索树

1. 二叉搜索树的概念和介绍

  二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

  （1）若它的左子树不为空，则左子树上所有节点的值都小于根节点的值

  （2）若它的右子树不为空，则右子树上所有节点的值都大于根节点的值

  （3）它的左右子树也分别为二叉搜索树

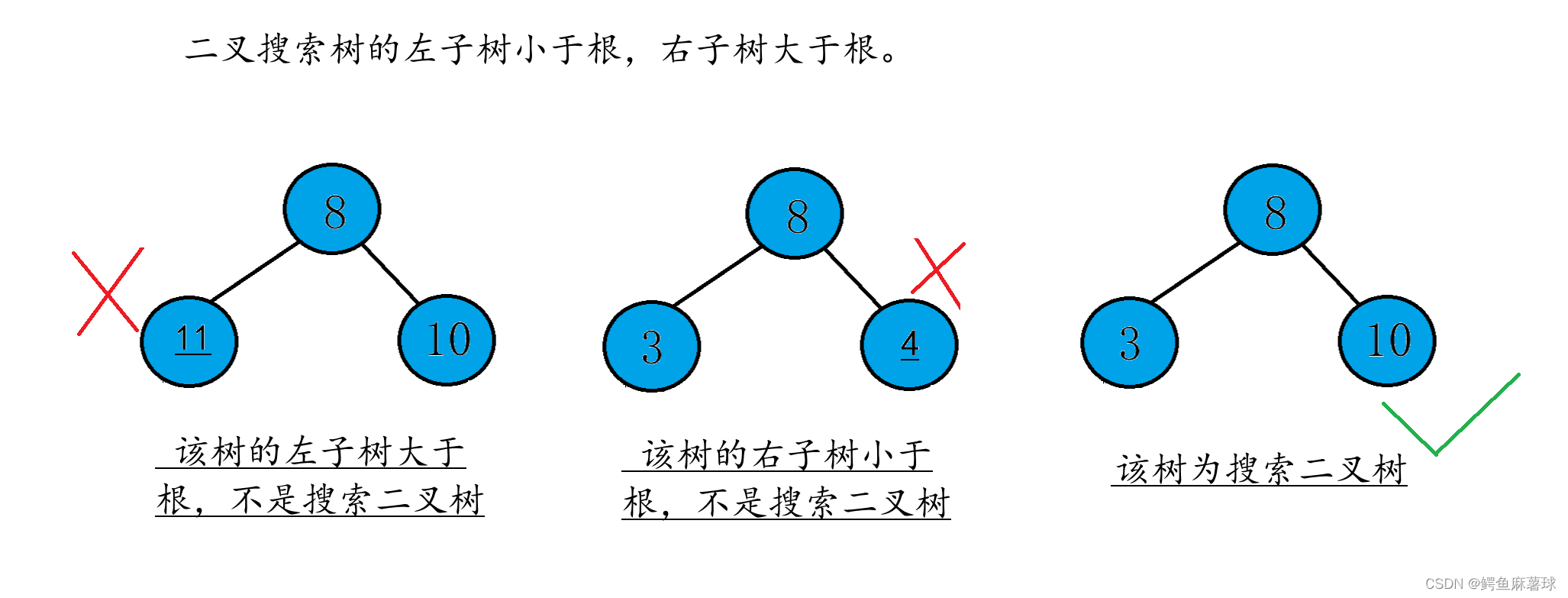
  二叉搜索树（Binary Search Tree）的每个节点包含三个属性：键（key）、左孩子（lchild）和右孩子（rchild）。 键用于存储节点的值，左孩子和右孩子分别指向左子树和右子树的根节点。

  二叉搜索树的结构类似于一个倒置的树，最底层的节点位于树的顶部，每个节点都有一个键值，并且每个节点的左子树上的所有节点的键值都小于该节点的键值，而右子树上的所有节点的键值都大于该节点的键值。这种结构使得二叉搜索树在处理有序数据时非常高效。

  基于以上性质，二叉搜索树在查找、插入和删除操作上具有较好的效率，时间复杂度为O(logn)。

  基于二叉搜索树的特殊结构，二叉搜索树的中序遍历（Inorder Traversal）按照左子树、根节点、右子树的顺序遍历二叉树，它会按照从大到小的顺序输出二叉树中的所有元素。

  以下这颗二叉搜索树的中序遍历结果：1 3 4 6 7 8 10 13 14

             

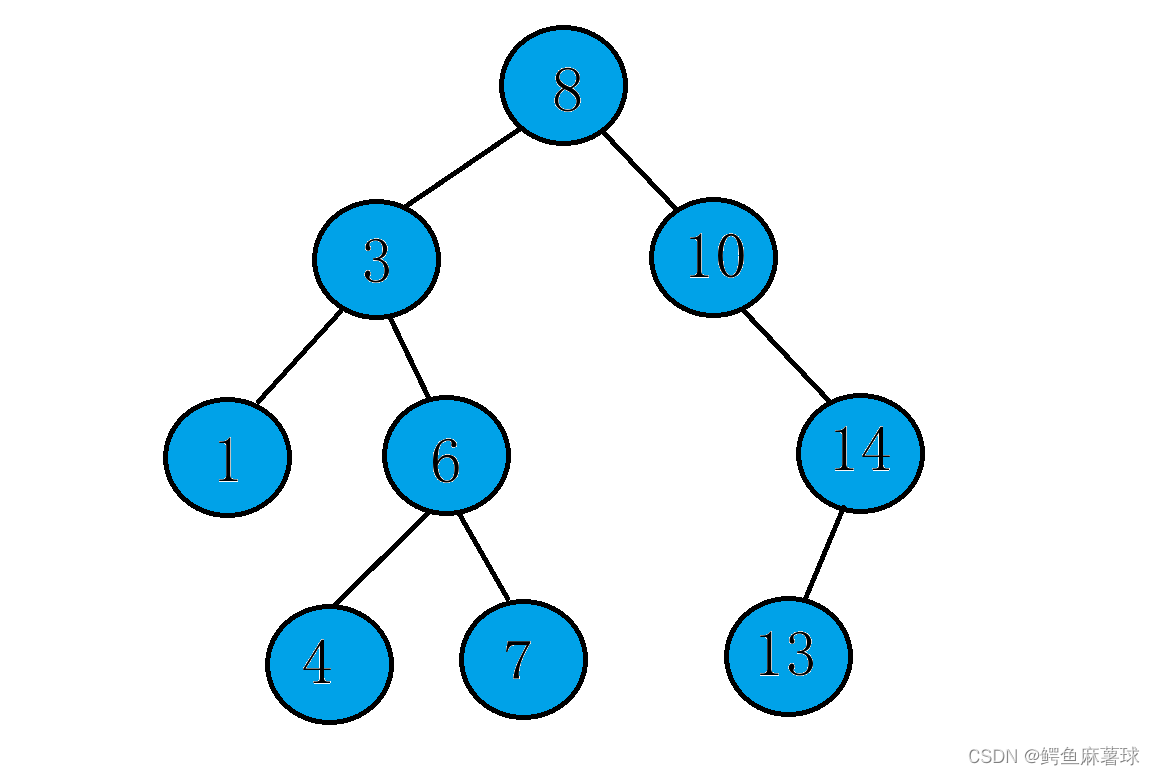
2. 二叉搜索树的简单实现

  和之前的二叉树实现类似，二叉搜索树的实现只需要在二叉树的实现基础上，将左右元素根据和根节点的大小，重新考虑排列顺序即可。

  定义二叉搜索树的节点：

//搜索二叉树创建节点
template<class K>
struct BSTreeNode
{//左右节点和节点值keyBSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;//二叉树节点构造函数BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}
};

  定义二叉搜索树类：

//创建二叉搜索树
template<class K>
class BSTree
{//便于书写BNode节点typedef BSTreeNode<K> BNode;public://二叉搜索树构造函数BSTree():_root(nullptr){}private:BNode* _root;
};

             

2.1二叉搜索树的插入

  二叉搜索树的插入过程可以分为以下步骤：

  （1）如果二叉搜索树为空，创建一个新的节点，并将待插入关键字放入新节点的数据域。将新节点作为根节点，左右子树均为空。

  （2）如果二叉搜索树非空，将待查找关键字与根节点关键字进行比较。如果小于根节点关键字，则将待查找关键字插入左子树中；如果大于根节点关键字，则将待查找关键字插入右子树中。

  重复上述步骤，直到找到合适的位置插入待插入的关键字。

  在插入过程中，需要保持二叉搜索树的性质：任意节点的左子树的所有节点的值都小于该节点的值，右子树的所有节点的值都大于该节点的值。如果插入后破坏了这种性质，需要进行调整。

 
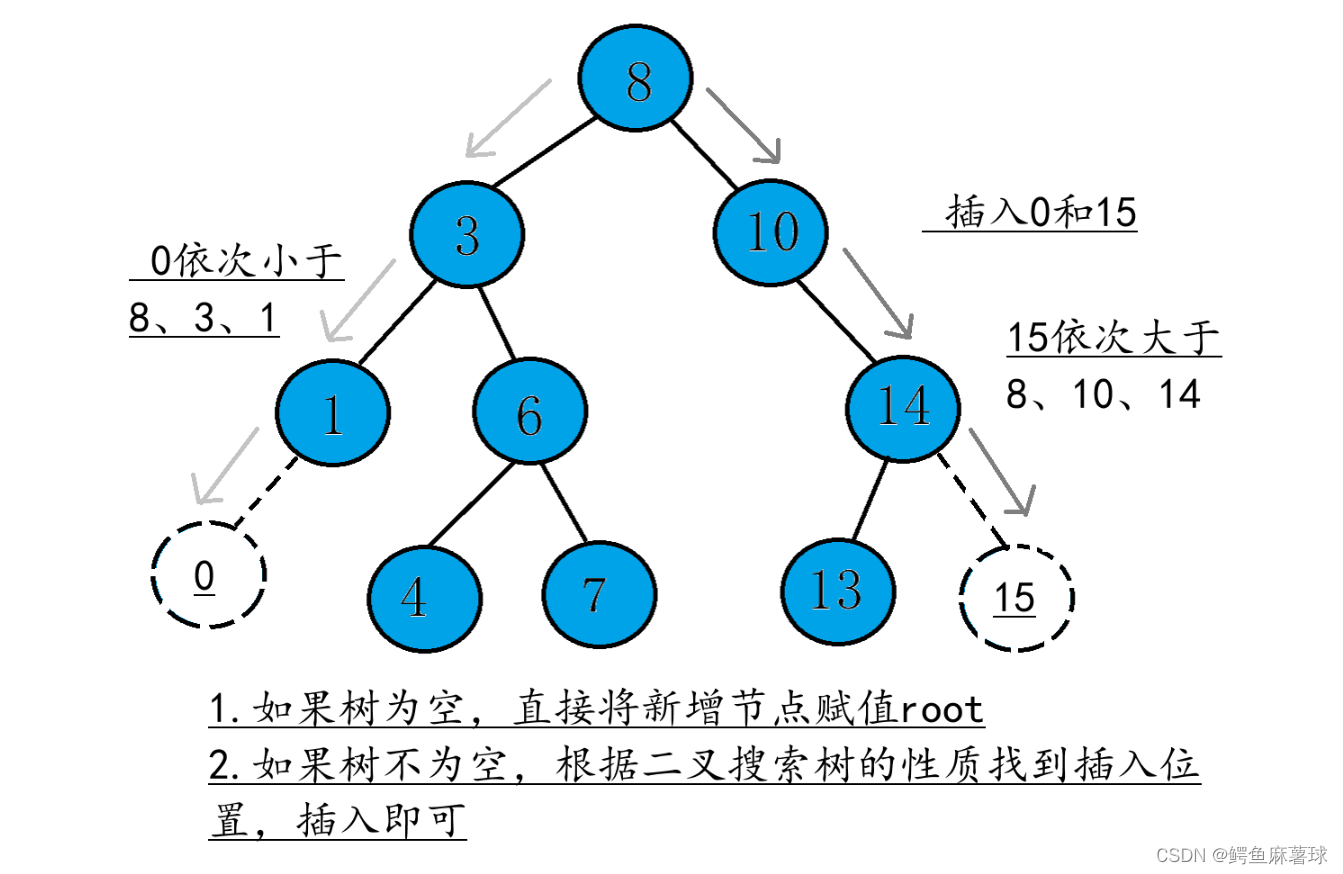
  非递归的实现：

//二叉树插入节点
bool BSInsert(const K& key)
{//如果该树为空树，直接创建节点if (_root == nullptr){_root = new BNode(key);return true;}//找到二叉树所在的节点BNode* parent = nullptr;BNode* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}//插入节点cur = new BNode(key);if (parent->_key > key){parent->_left = cur;}else {parent->_right = cur;}return true;
}

 
  递归的实现：

bool _BSInsertR(BNode*& root, const K& key)//这里传&,直接可以得到地址
{if (root == nullptr){root = new BNode(key);return true;}if (root->_key < key){_BSInsertR(root->_right, key);}else if (root->_key > key){_BSInsertR(root->_left, key);}else{return false;}
}

             

2.2二叉搜索树的查找

  二叉搜索树的查找实现过程可以分为以下步骤：

  （1）将待查找关键字与根节点关键字进行比较。如果相等，则找到了目标关键字，查找结束。

  （2）如果待查找关键字小于根节点关键字，则将待查找关键字放入左子树中继续查找。

  （3）如果待查找关键字大于根节点关键字，则将待查找关键字放入右子树中继续查找。

  重复上述步骤，直到找到目标关键字，或者搜索到了空节点（表示未找到目标关键字）。

  在查找过程中，由于二叉搜索树是基于二分的思想，所以每次比较都可以排除一半的搜索空间，因此时间复杂度为O(logn)。

 
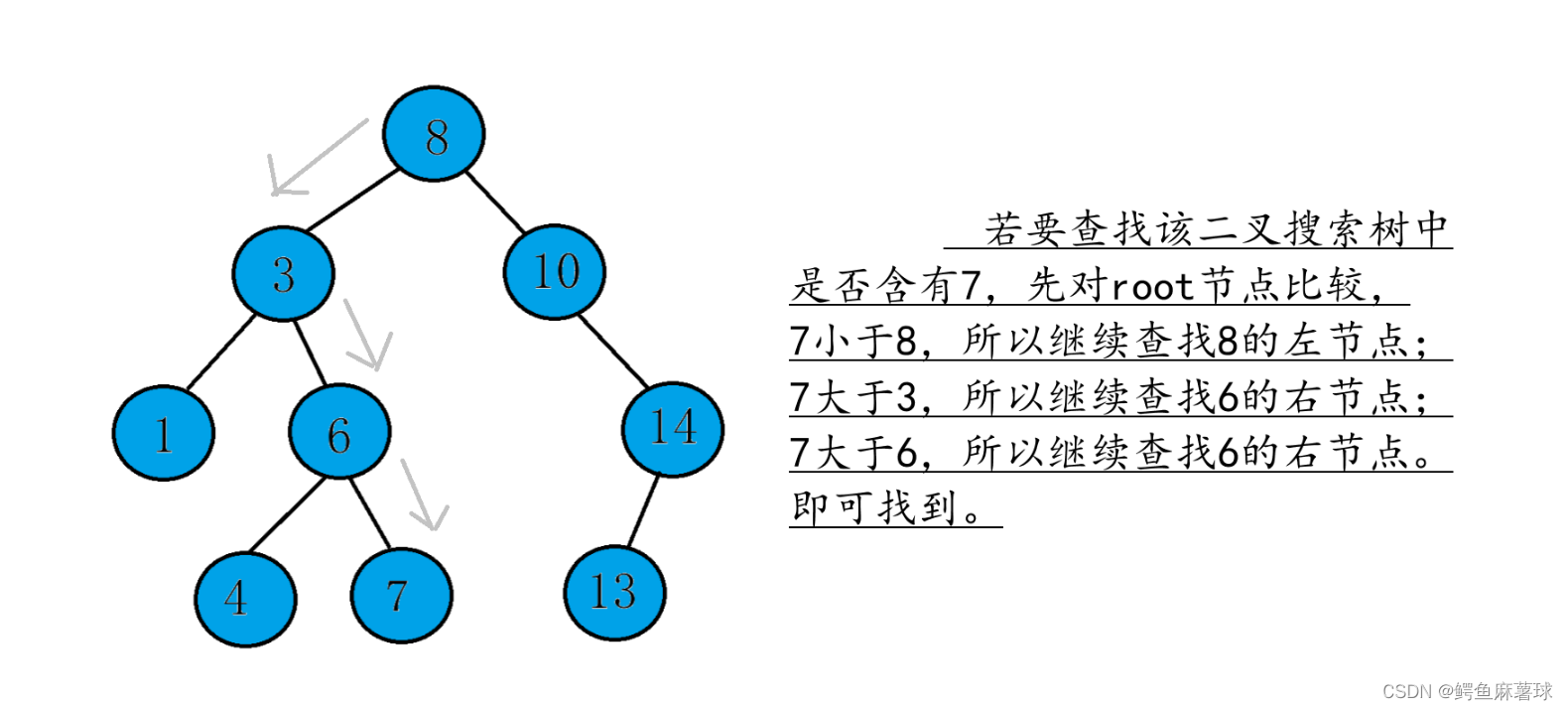
  非递归实现：

//查找二叉树的节点
bool BSFind(const K& key)
{BNode* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{return true;}}return false;
}

  递归实现：

bool _BSFindR(BNode* root, const K& key)
{if (root == nullptr){return false;}if (root->_key < key){return _BSFindR(root->_right, key);}else if (root->_key > key){return _BSFindR(root->_left, key);}else{return true;}
}

             

2.3二叉搜索树的遍历

  二叉搜索树常使用中序遍历，而不是前序遍历和后序遍历。

  因为中序遍历的特点是先访问左子树，然后访问根节点，最后访问右子树。 在访问左子树时，先访问左子树的左子树，再访问左子树的右子树；在访问右子树时，先访问右子树的左子树，再访问右子树的右子树。

  二叉搜索树中序遍历的结果是按照从小到大的顺序输出二叉搜索树中的所有元素。

  二叉搜索树的中序遍历过程可以分为以下步骤：

  （1）首先遍历左子树，访问左子树中的所有节点，并按照中序遍历的顺序递归地访问它们的右子树。

  （2）然后访问根节点。

  （3）最后遍历右子树，访问右子树中的所有节点，并按照中序遍历的顺序递归地访问它们的左子树。

  递归实现：

void _BSInOrder(BNode* root)
{if (root == nullptr){return;}_BSInOrder(root->_left);printf("%d ", root->_key);_BSInOrder(root->_right);
}

             

2.4二叉搜索树的删除

  二叉搜索树的删除操作可以按照以下步骤实现：

  （1）首先，找到要删除的节点。可以通过中序遍历或者二分查找等方式找到要删除的节点。

  （2）如果要删除的节点是叶子节点（没有子节点），直接将该节点从二叉搜索树中删除即可。

  （3）如果要删除的节点只有一个子节点，将该节点的子节点与其父节点相连，删除该节点即可。

  （4）如果要删除的节点有两个子节点，需要找到该节点的左子树中的最大节点（或者右子树中的最小节点），用该节点代替要删除的节点的位置，然后删除该最小（或最大）节点。

  在实现删除操作时，需要注意保持二叉搜索树的性质，即任意节点的左子树的所有节点的值都小于该节点的值，右子树的所有节点的值都大于该节点的值。同时，删除操作可能会导致二叉搜索树的平衡被破坏，需要进行相应的调整操作。

  （1）当没有叶子结点，或者只有一个子节点的情况：

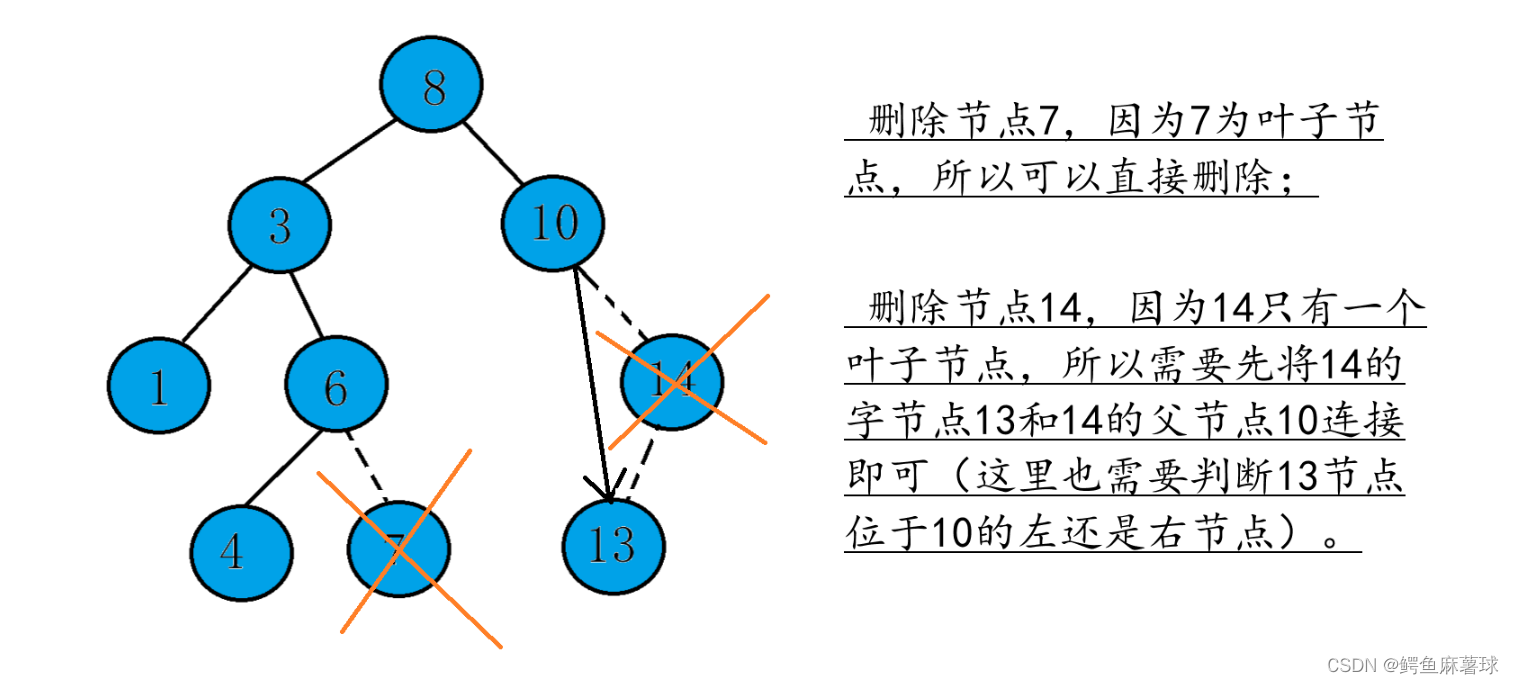
  （2）当左右都有子节点的情况：

 
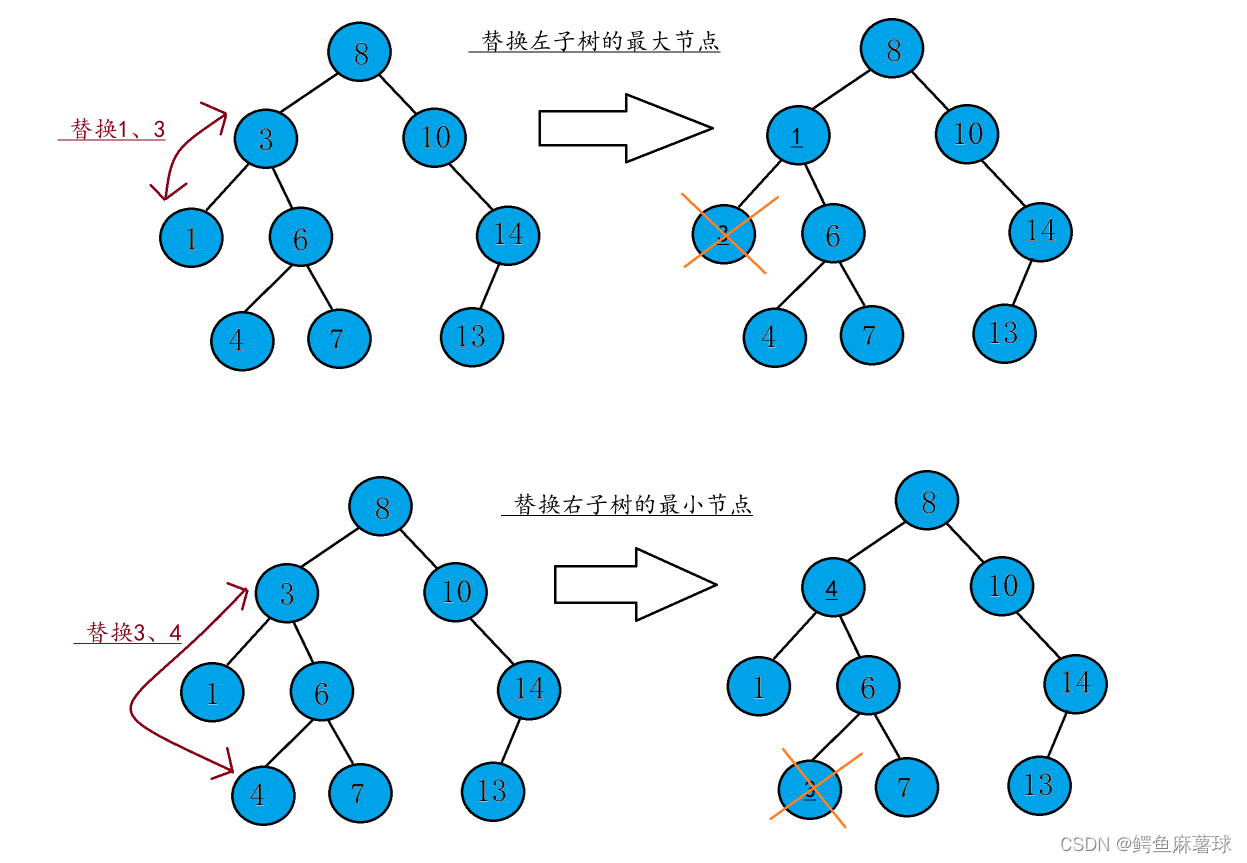
  非递归实现：

//删除二叉树中的节点
bool BSErase(const K& key)
{BNode* cur = _root;BNode* parent = nullptr;//先要找到所删除的节点while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else//找到了所要删除的节点{if (cur->_left == nullptr)//当左节点为空节点{if (cur == _root)//cur为根节点{_root = cur->_right;}else//cur不为空节点{if (parent->_right == cur){parent->_right = cur->_right;}else{parent->_left = cur->_right;}}}else if(cur->_right==nullptr)//当右节点为空节点{if (cur == _root)//cur为空节点{_root = cur->_left;}else//cur不为空节点{if (parent->_right == cur){parent->_right = cur->_left;}else{parent->_left = cur->_left;}}}else//当左右节点都不为空节点{//找代替节点BNode* parent = cur;BNode* leftMax = cur->_left;while (leftMax->_right){parent = leftMax;leftMax = leftMax->_right;}swap(cur->_key, leftMax->_key);if (parent->_left == leftMax){parent->_left = leftMax->_left;}else{parent->_right = leftMax->_left;}cur=leftMax;}delete cur;return true;}}return false;
}

  递归实现：

bool _BSEraseR(BNode* &root, const K& key)
{if (root == nullptr){return false;}if (root->_key < key){_BSEraseR(root->_right, key);}else if (root->_key > key){_BSEraseR(root->_left, key);}else{BNode* del = root;//1.左为空//2.右为空//3.左右都不为空if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{BNode* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}swap(root->_key, leftMax->_key);return _BSEraseR(root->_left, key);}delete del;return true;}
}

             

2.5完整代码和测试

  完整代码：

#pragma once//搜索二叉树创建节点
template<class K>
struct BSTreeNode
{//左右节点和节点值keyBSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;//二叉树节点构造函数BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}
};//创建搜索二叉树
template<class K>
class BSTree
{//便于书写BNode节点typedef BSTreeNode<K> BNode;public://搜索二叉树构造函数BSTree():_root(nullptr){}//二叉树插入节点bool BSInsert(const K& key){//如果该树为空树，直接创建节点if (_root == nullptr){_root = new BNode(key);return true;}//找到二叉树所在的节点BNode* parent = nullptr;BNode* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}//插入节点cur = new BNode(key);if (parent->_key > key){parent->_left = cur;}else {parent->_right = cur;}return true;}//查找二叉树的节点bool BSFind(const K& key){BNode* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{return true;}}return false;}//删除二叉树中的节点bool BSErase(const K& key){BNode* cur = _root;BNode* parent = nullptr;//先要找到所删除的节点while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else//找到了所要删除的节点{if (cur->_left == nullptr)//当左节点为空节点{if (cur == _root)//cur为根节点{_root = cur->_right;}else//cur不为空节点{if (parent->_right == cur){parent->_right = cur->_right;}else{parent->_left = cur->_right;}}}else if(cur->_right==nullptr)//当右节点为空节点{if (cur == _root)//cur为空节点{_root = cur->_left;}else//cur不为空节点{if (parent->_right == cur){parent->_right = cur->_left;}else{parent->_left = cur->_left;}}}else//当左右节点都不为空节点{//找代替节点BNode* parent = cur;BNode* leftMax = cur->_left;while (leftMax->_right){parent = leftMax;leftMax = leftMax->_right;}swap(cur->_key, leftMax->_key);if (parent->_left == leftMax){parent->_left = leftMax->_left;}else{parent->_right = leftMax->_left;}cur=leftMax;}delete cur;return true;}}return false;}//二叉树的中序遍历void BSInOrder(){_BSInOrder(_root);cout << endl;}//递归实现二叉树的查找bool BSFindR(const K& key){return _BSFindR(_root, key);}//递归实现二叉树的插入节点bool BSInsertR(const K& key){return _BSInsertR(_root, key);}//递归实现二叉树的删除节点bool BSEraseR(const K& key){return _BSEraseR(_root, key);}private://递归二叉树删除的封装实现bool _BSEraseR(BNode* &root, const K& key){if (root == nullptr){return false;}if (root->_key < key){_BSEraseR(root->_right, key);}else if (root->_key > key){_BSEraseR(root->_left, key);}else{BNode* del = root;//1.左为空//2.右为空//3.左右都不为空if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{BNode* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}swap(root->_key, leftMax->_key);return _BSEraseR(root->_left, key);}delete del;return true;}}//递归二叉树插入的封装实现bool _BSInsertR(BNode*& root, const K& key)//这里传&,直接可以得到地址{if (root == nullptr){root = new BNode(key);return true;}if (root->_key < key){_BSInsertR(root->_right, key);}else if (root->_key > key){_BSInsertR(root->_left, key);}else{return false;}}//递归二叉树查找的封装实现bool _BSFindR(BNode* root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return _BSFindR(root->_right, key);}else if (root->_key > key){return _BSFindR(root->_left, key);}else{return true;}}//为了递归实现，进行一层封装void _BSInOrder(BNode* root){if (root == nullptr){return;}_BSInOrder(root->_left);printf("%d ", root->_key);_BSInOrder(root->_right);}private:BNode* _root;
};

 
  简单测试：

#define _CRT_SECURE_NO_WARNINGS 1#include<iostream>
using namespace std;#include"BinarySearchTree.h"void BSTree_test1()
{BSTree<int> t;t.BSInsert(5);t.BSInsert(8);t.BSInsert(6);t.BSInsert(1);t.BSInsert(3);t.BSInsert(2);t.BSInsert(4);t.BSInOrder();cout << "是否存在二叉树的值为1:";if (t.BSFind(1))cout << "存在";else cout << "不存在";cout << endl;int arr[] = { 5,3,1,2,4,9,8,6,7,10 };BSTree<int> t1;for (auto e : arr){t1.BSInsert(e);}t1.BSInOrder();t1.BSErase(3);t1.BSInOrder();cout << "是否存在二叉树的值为1:";if (t1.BSFindR(1))cout << "存在";else cout << "不存在";cout << endl;t1.BSInsertR(11);t1.BSInOrder();t1.BSEraseR(11);t1.BSInOrder();}int main()
{BSTree_test1();return 0;
}

这里就是数据结构中二叉搜索树的基本介绍了😉
如有错误❌望指正，最后祝大家学习进步✊天天开心✨🎉