【高阶数据结构】红黑树 {概念及性质;红黑树的结构;红黑树的实现;红黑树插入操作详细解释;红黑树的验证}
红黑树
一、红黑树的概念
红黑树(Red Black Tree) 是一种自平衡二叉查找树,在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
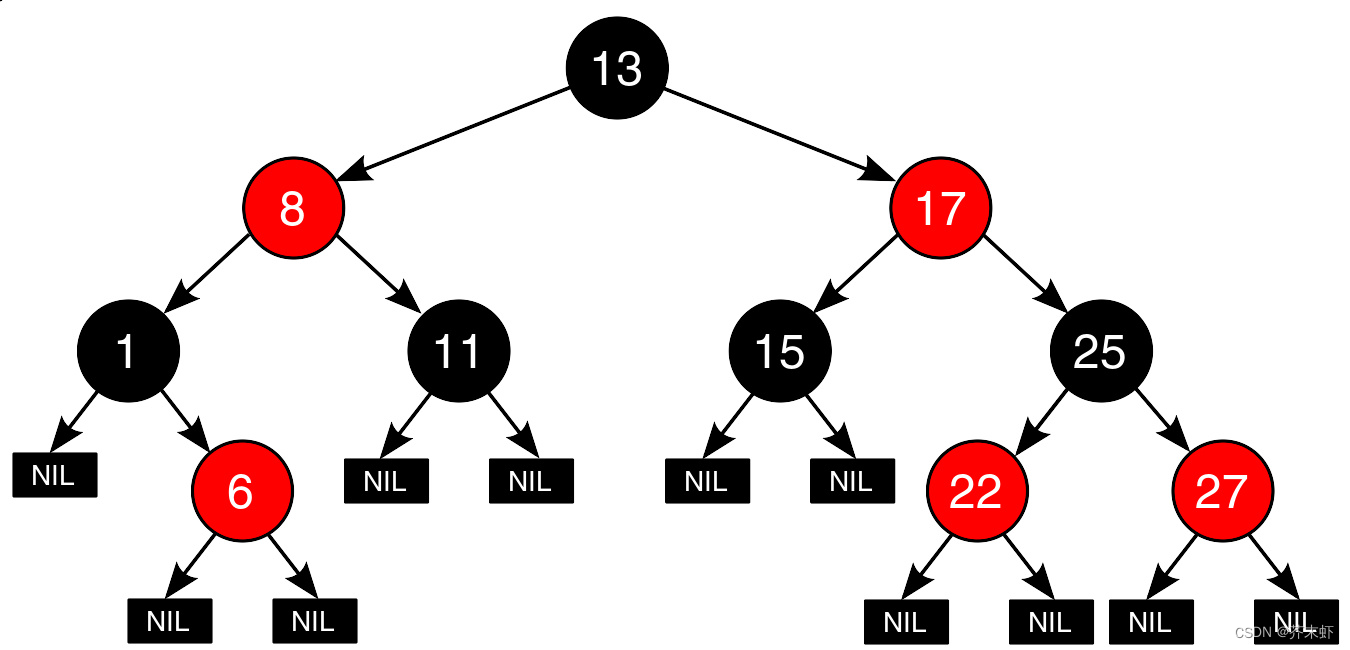
AVL树 VS 红黑树
-
红黑树是一种特化的AVL树,都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡,从而获得较高的查找性能。
-
AVL树要求每棵子树的左右高度差不超过1,是严格平衡;而红黑树要求最长路径不超过最短路径的2倍,是接近平衡。
-
而红黑树是一种AVL树的变体,它要求最长路径不超过最短路径的2倍,左右子树高差有可能大于 1。所以红黑树不是严格意义上的平衡二叉树(AVL),但对之进行平衡的代价较低, 其平均统计性能要强于 AVL 。
-
相对而言,插入或删除同样的数据,AVL树旋转的更多,而红黑树则旋转的更少效率相对较高。
二、红黑树的性质
红黑树是每个结点都带有颜色属性的二叉查找树,颜色或红色或黑色。 在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
-
性质1. 结点是红色或黑色。
-
性质2. 根结点是黑色。
-
性质3. 每个红色结点的两个子结点都是黑色。(每条路径上不能有两个连续的红色结点)
-
性质4. 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。 (每条路径上的黑色节点数量相同)
-
性质5. 所有NIL结点都是黑色的。(NIL节点即空结点)
这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树。
是性质3导致路径上不能有两个连续的红色结点确保了这个结果。最短的可能路径都是黑色结点,最长的可能路径有交替的红色和黑色结点。因为根据性质4所有路径都有相同数目的黑色结点,这就表明了没有路径能多于任何其他路径的两倍长。
思考:新插入的节点应该设为黑色还是红色?
如果将新插入的节点设为黑色,不管插到那条路径都必然违反性质4。
如果将新插入的节点设为红色:如果父节点是红色则违反性质3,需要进行调整;如果父节点是黑色就正常插入,无需调整。
对比两种情况,最终选择将新插入的节点设为红色。
三、STL中的红黑树结构
- 为了后续实现关联式容器map/set,STL红黑树的实现中增加一个头结点;
- 因为根节点必须为黑色,为了与根节点进行区分,将头结点给成红色;
- 并且让头结点的
_parent域指向红黑树的根节点,_left域指向红黑树中最小的节点,_right域指向红黑树中最大的节点。

头结点的作用:
- STL明确规定,begin()与end()代表的是一段前闭后开的区间,而对红黑树进行中序遍历后,可以得到一个有序的序列,因此:begin()可以放在红黑树中最小节点(即最左侧节点)的位置,end()放在最大节点(最右侧节点)的下一个位置,关键是最大节点的下一个位置在哪块?
- 能否给成nullptr呢?答案是行不通的,因为对end()位置的迭代器进行–操作,必须要能找最后一个元素,此处就不行,因此最好的方式是将end()放在头结点的位置:
四、核心结构
enum Color{RED,BLACK
};
//红黑树的节点
template <class K, class V>
struct RBTreeNode{ RBTreeNode<K,V> *_left;RBTreeNode<K,V> *_right;RBTreeNode<K,V> *_parent;pair<K,V> _kv;Color _color; //颜色属性RBTreeNode(const pair<K,V> &kv=pair<K,V>(), Color color = RED):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_color(color){}
};//红黑树结构
template <class K, class V>
class RBTree{ typedef RBTreeNode<K,V> Node;Node *_phead; //指向头结点的指针public:RBTree(){_phead = new Node; //红黑树的头结点_phead->_left = _phead; //起初先让头结点的左右指针指向自己_phead->_right = _phead;}Node*& GetRoot(){ //返回根节点指针的引用,便于进行修改return _phead->_parent; }//........
private:Node* LeftMost(){ //返回红黑树的最左节点指针Node *root = GetRoot();if(root == nullptr) //如果根节点为空,就返回_pheadreturn _phead;else{Node *left = root;while(left->_left!=nullptr){left = left->_left;}return left;}}Node* RightMost(){ //返回红黑树的最右节点指针Node *root = GetRoot();if(root == nullptr) //如果根节点为空,就返回_pheadreturn _phead;else{Node *right = root;while(right->_right!=nullptr){right = right->_right;}return right;}}//......
};
五、红黑树的插入操作
红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可分为两步:
-
按照二叉搜索的树规则插入新节点
-
检测新节点插入后,红黑树的性质是否造到破坏。因为新节点的默认颜色是红色,因此:
- 如果新插入的节点是根节点,需要将节点变为黑色以满足性质2。
- 如果父节点是黑色的,没有违反红黑树的任何性质,则不需要调整;
- 但如果父节点颜色为红色时,就违反了性质3:路径上不能有两个连续的红色结点。此时需要对红黑树分情况来讨论:
在讲解情况三、四、五之前,先说明一下:
- cur为当前节点(关注节点),p(parent)为父节点,g(grandparent)为祖父节点,u(uncle)为叔叔节点;
- cur不一定就是新插入的节点,也有可能是因为 cur 的子树在调整的过程中将 cur 节点的颜色由黑色改成红色。
5.1 情况一:u存在且为红
情况一: cur为红,p为红,g为黑,u存在且为红
抽象分析:

- 因为cur和p都为红色违反性质3,所以一定要把p变为黑色。
- 但只变p又违反性质4各路径上黑色节点的数量不同,所以要把u也变为黑色。
- 但原来所有路径上只有1个黑色节点(可见的)而现在变为2个。如果g树是子树,又会使整棵树违反性质4。所以要把g变为红色。
- g的父节点也可能是红色,所以要继续向上调整。
解决方式:变色并继续向上调整
- 将p,u都改为黑色,g改为红色;
- 如果g不为根,就把g当成cur继续向上调整;
- 如果g为根,就把g变为黑色。性质2:根节点是黑色的。
具体分析:
cur就是新插入的节点:
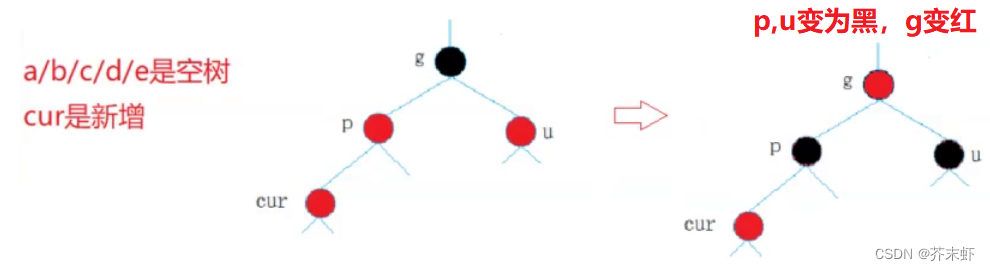
cur节点原来是黑色之后又被调整为红色:
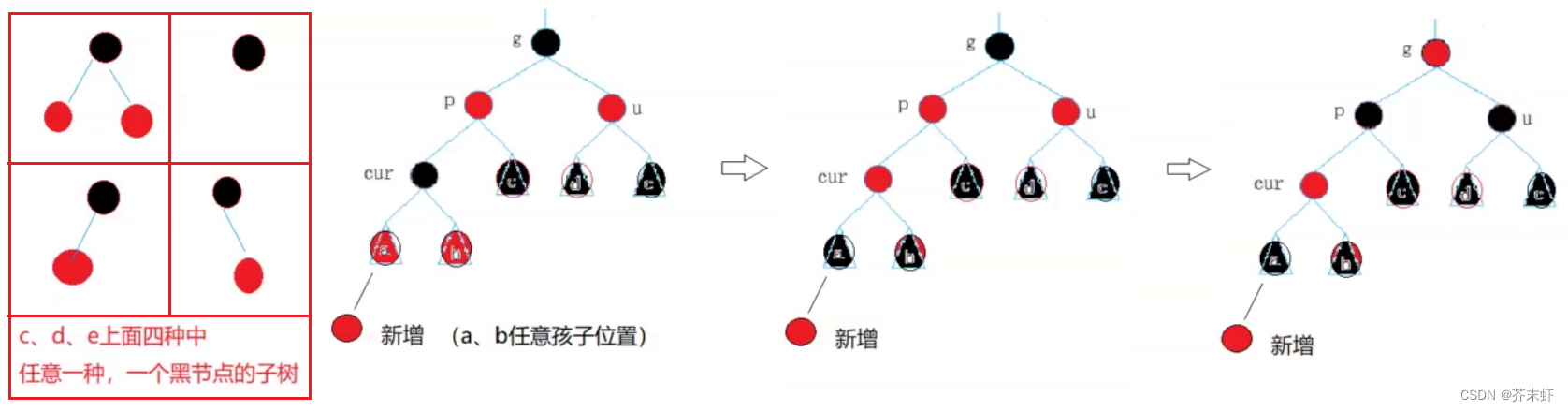
注意:a,b,c,d,e可能是连续的几层黑色节点(要求每条路径的黑色节点数量相同),然后才出现上述情况。因为情况太多,过于复杂故作省略。
5.2 情况二:u不存在/u存在且为黑(单旋)
情况二: cur为红,p为红,g为黑,u不存在/u存在且为黑(单旋)
抽象分析:
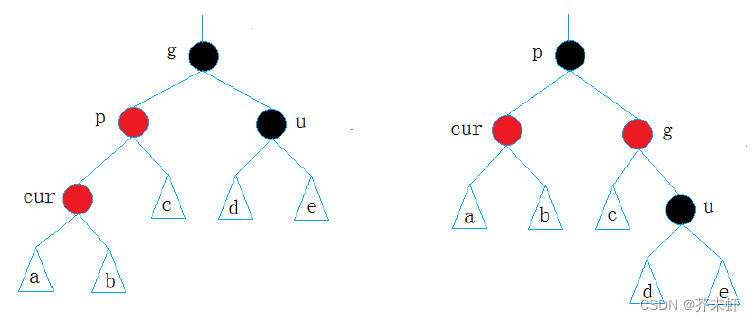
- 因为cur和p都为红色违反性质3,所以一定要把p变为黑色。
- 但只变p使左路黑节点+1违反性质4,因此还要以g为轴点右单旋,使左路黑节点-1。
- 但此时由于右单旋使右路黑节点+1,所以要将g变为红色,右路黑节点-1。最终满足性质4。
解决方式:单旋+变色
- 如果p为g的左孩子,cur为p的左孩子(左左),则对g进行右单旋;
- 如果p为g的右孩子,cur为p的右孩子(右右),则对g进行左单旋;
- p、g变色–p变黑色,g变红色。
- 完成旋转变色后每条路径的黑节点数量相同且与插入前也相同,并且根节点为黑色不需要继续往上处理。
具体分析:u 的情况有两种
uncle节点不存在:
如果 u 节点不存在,则 cur 一定是新插入节点,因为如果 cur 不是新插入节点,则 cur 和 p 一定有一个节点的颜色是黑色,就不满足性质4:每条路径黑色节点个数相同。
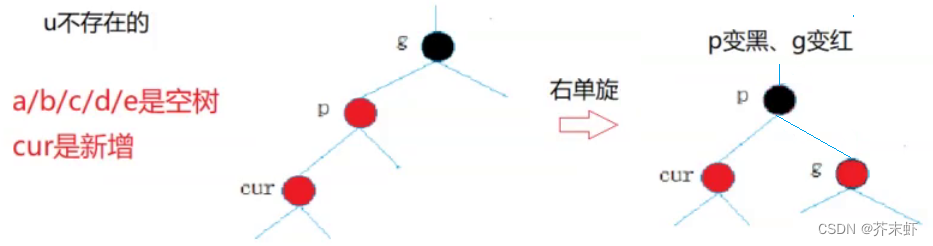
uncle节点存在且为黑色:
如果 u 节点存在且为黑色,那么 cur 节点原来的颜色也一定是黑色的,现在看到其是红色的原因是因为 cur 的子树在调整的过程中将 cur 节点的颜色由黑色改成红色。
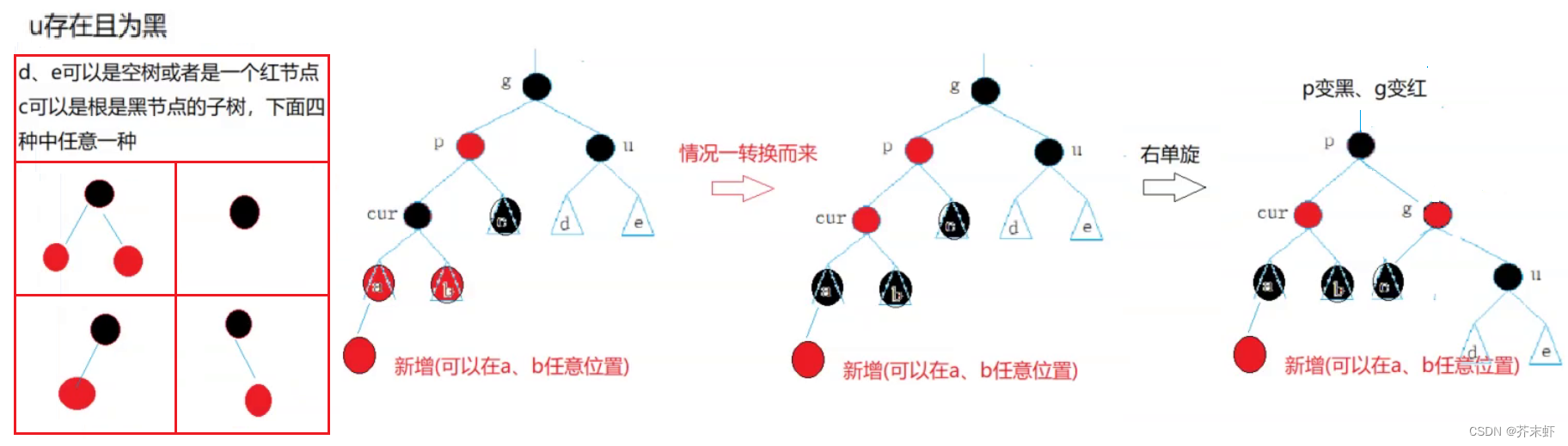
注意:a,b,c,d,e可能是连续的几层黑色节点(要求每条路径的黑色节点数量相同),然后才出现上述情况。因为情况太多,过于复杂故作省略。
5.3 情况三:u不存在/u存在且为黑(双旋)
情况三: cur为红,p为红,g为黑,u不存在/u存在且为黑(双旋)
抽象图:
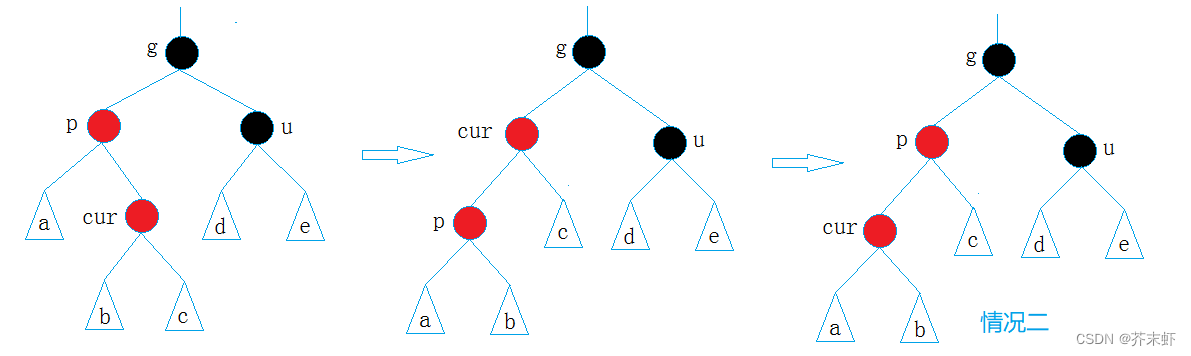
情况三先以p为轴点左单旋,转换为情况二。
解决方式:双旋+变色
- p为g的左孩子,cur为p的右孩子(左右),则先对p做左单旋,再对g做右单旋;
- p为g的右孩子,cur为p的左孩子(右左),则先对p做右单旋,再对g做左单旋;
- cur、g变色–cur变黑色,g变红色。
- 完成旋转变色后每条路径的黑节点数量相同且与插入前也相同,并且根节点为黑色不需要继续往上处理。
具体分析:
uncle节点不存在
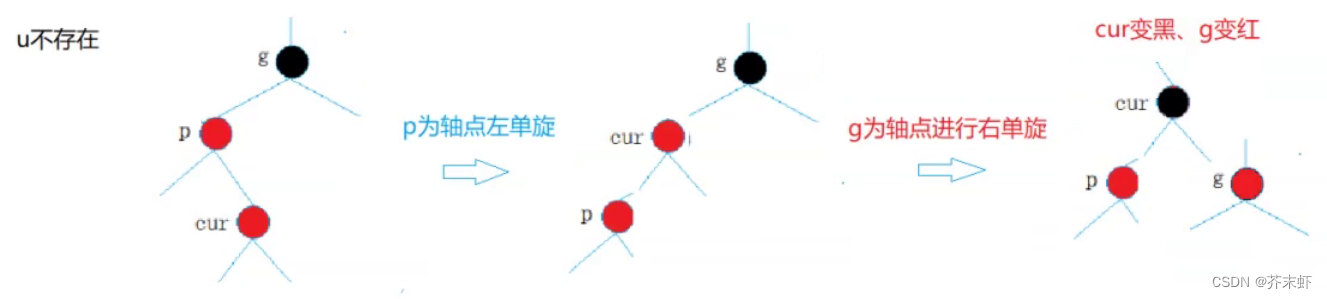
uncle节点存在且为黑色:
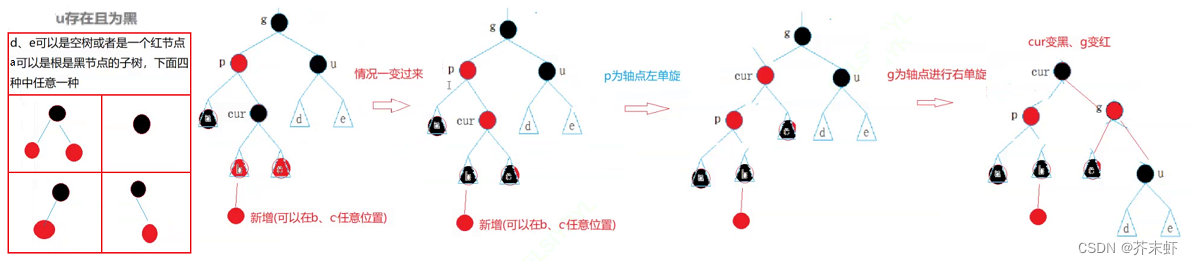
注意:a,b,c,d,e可能是连续的几层黑色节点(要求每条路径的黑色节点数量相同),然后才出现上述情况。因为情况太多,过于复杂故作省略。
总结:
- 二叉树插入操作的难点在于通过变色和旋转操作恢复红黑树的性质,性质得到满足红黑树就能做到近似平衡:最长路径不超过最短路径的两倍。
- 恢复的最终目的:1.关注子树满足红黑树的所有性质 2.插入前后关注子树每条路径的黑节点数量不变(保证整棵树的性质4)
5.4 插入代码
bool Insert(const pair<K,V> &kv)
{//1. 按照二叉搜索的树规则插入新节点Node* &root = GetRoot(); //这里注意要用引用接收返回值if(root == nullptr){//如果新插入的节点是根节点,需要将节点变为黑色以满足性质2root = new Node(kv, BLACK); //因为GetRoot返回指针的引用,所以改的实际是_phead->_parentroot->_parent = _phead;_phead->_left = root;_phead->_right = root;return true;}Node *cur = root;Node *parent = nullptr;while(cur != nullptr){if(kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if(kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv,RED); //新插入的节点默认是红色的if(kv.first > parent->_kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//2.检测新节点插入后,红黑树的性质是否造到破坏。//如果父节点是黑色的,没有违反红黑树的任何性质,则不需要调整;//但如果父节点颜色为红色时,就违反了性质3:路径上不能有两个连续的红色结点。//上一次循环中grandparent 为根节点,此次循环parent == _pheadwhile(parent != _phead && parent->_color == RED) {Node *grandparent = parent->_parent;//断言检查:grandparent一定不为空且为黑色!assert(grandparent != nullptr);assert(grandparent->_color == BLACK);Node *uncle = grandparent->_left;if(parent == grandparent->_left)uncle = grandparent->_right;if(uncle != nullptr && uncle->_color == RED) //情况一:uncle存在且为红{parent->_color = uncle->_color = BLACK; //变色grandparent->_color = RED;cur = grandparent; //继续向上调整parent = cur->_parent;}else //情况二、三:uncle不存在或uncle存在且为黑{if(parent == grandparent->_left){if(cur == parent->_left) //左左{RotateR(grandparent); //右单旋parent->_color = BLACK; //变色grandparent->_color = RED;}else{ //左右RotateL(parent); //左右双旋RotateR(grandparent);cur->_color = BLACK; //变色grandparent->_color = RED;}}else{if(cur == parent->_right) //右右{RotateL(grandparent); //左单旋parent->_color = BLACK; //变色grandparent->_color = RED;}else{ //右左RotateR(parent); //右左双旋RotateL(grandparent);cur->_color = BLACK; //变色grandparent->_color = RED;}}//旋转变色后无需继续调整,直接退出循环。break; } //end of else} //end of while//如果在调整过程中将根节点变为红色,记得重新变回黑色。if(parent == _phead) root->_color = BLACK;//令头节点的左指针指向红黑树的最左节点_phead->_left = LeftMost();//令头节点的右指针指向红黑树的最右节点_phead->_right = RightMost();return true;
}
5.5 旋转代码
void RotateL(Node *parent){Node *subR = parent->_right;Node *subRL = subR->_left;Node *ppNode = parent->_parent;parent->_right = subRL;if(subRL != nullptr){subRL->_parent = parent;}subR->_left = parent;parent->_parent = subR;if(ppNode == _phead){_phead->_parent = subR;}else{if(ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}}subR->_parent = ppNode;
}void RotateR(Node *parent){Node *subL = parent->_left;Node *subLR = subL->_right;Node *ppNode = parent->_parent;parent->_parent = subL;subL->_right = parent;parent->_left = subLR;if(subLR != nullptr)subLR->_parent = parent;if(ppNode == _phead){ppNode->_parent = subL;}else{if(ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}}subL->_parent = ppNode;
}
六、查找和遍历
Node* Find(const K &k){Node *root = GetRoot();if(root == nullptr)return nullptr;Node *cur = root;while(cur != nullptr){if(k > cur->_kv.first){cur = cur->_right;}else if(k < cur->_kv.first){cur = cur->_left;}else{return cur;}}return nullptr;
}void Inorder(){_Inorder(GetRoot());cout << endl;
}void _Inorder(Node *root){if(root == nullptr) return; _Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << " ";_Inorder(root->_right);
}
七、红黑树的验证
红黑树的检测分为两步:
- 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
- 检测其是否满足红黑树的性质
bool IsValidRBTree(){Node *root = GetRoot();//空树也是红黑树if(root == nullptr) return true;//检查性质2:if(root->_color != BLACK){cout << "违反性质2:根节点不为黑色!" << endl;return false;}//检查性质3,4:int benchmark = 0;return _IsValidRBTree(root, 0, benchmark);
}//blacknum:用于记录当前路径的黑色节点个数,不能传引用。
//benchmark:用于记录第一条路径的黑色节点个数。需要传引用,返回给上层递归。
bool _IsValidRBTree(Node *root, int blacknum, int &benchmark){if(root == nullptr){if(benchmark == 0) //表示第一条路径遍历完{benchmark = blacknum; //记录第一条路径的黑色节点个数return true;}else{if(blacknum != benchmark) //如果其他路径的blacknum与第一条路径不同,说明违反性质4{cout << "违反性质4:从任意节点到每个叶子节点的所有路径都包含相同数目的黑色节点!" << endl;return false;}else{return true;}}}//检查性质3:if(root->_color == RED && root->_parent->_color == RED){cout << "违反性质3:路径上有两个连续的红色节点!" << endl;return false;}if(root->_color == BLACK){++blacknum; }return _IsValidRBTree(root->_left, blacknum, benchmark)&& _IsValidRBTree(root->_right, blacknum, benchmark);
}
相关文章:

【高阶数据结构】红黑树 {概念及性质;红黑树的结构;红黑树的实现;红黑树插入操作详细解释;红黑树的验证}
红黑树 一、红黑树的概念 红黑树(Red Black Tree) 是一种自平衡二叉查找树,在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有…...

获取对象占用内存
添加依赖 <dependency><groupId>org.apache.lucene</groupId><artifactId>lucene-core</artifactId><version>4.0.0</version> </dependency>添加vm启动参数 --add-opens java.base/java.langALL-UNNAMED --add-opens java.ba…...
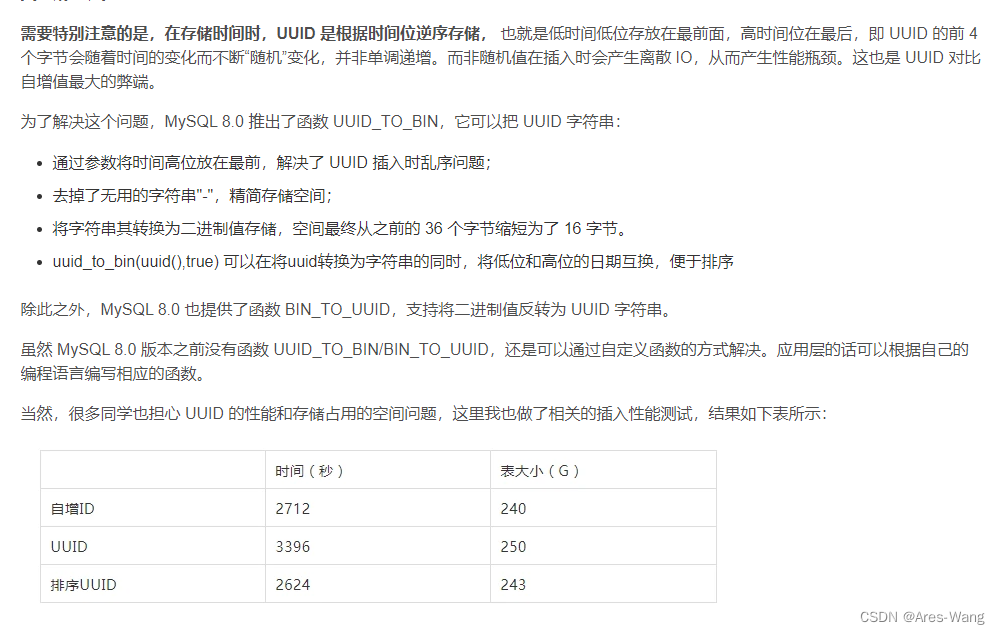
mysql UUID 作为主键的问题
UUID 在MySQL中,可以使用UUID()函数来生成一个新的UUID值。该函数的返回值是一个字符串类型,表示一个32位的十六进制数字,其中包含4个连字符“-”,例如:“6ccd780c-baba-1026-9564-0040f4311e29”。 varchar(32) 32*4…...

2023高教社杯全国大学生数学建模竞赛选题建议
如下为C君的2023高教社杯全国大学生数学建模竞赛(国赛)选题建议, 提示:DS C君认为的难度:C<B<A,开放度:B<A<C 。 D、E题推荐选E题,后续会直接更新E论文和思路…...

分类预测 | MATLAB实现GRNN广义回归神经网络多特征分类预测
分类预测 | MATLAB实现GRNN广义回归神经网络多特征分类预测 目录 分类预测 | MATLAB实现GRNN广义回归神经网络多特征分类预测分类效果基本介绍模型描述预测过程程序设计参考资料分类效果 基本介绍 MATLAB实现GRNN广义回归神经网络多特...

低功耗窗帘电机解决方案成功应用并通过 Matter 1.1 认证
Nordic Semiconductor官方宣布与HooRii Tech(和众科技)携手合作,基于 Nordic nRF52840 芯片平台打造的 HRN71模组,成功赋能低功耗窗帘电机品牌发布Matter产品。低功耗窗帘电机获得 Matter 1.1 认证意味着它具有与其他 Matter 认证…...

如何修复老照片?老照片修复翻新的方法
老旧照片,尤其是黑白照片,往往因为年代久远、保存方式不当等原因而出现褪色、污损、划痕等问题,会比较难以修复,就算是技术精湛的专业修复师,也是需要投入极大时间精力的,效果也是不可预料的。 修复老照片…...
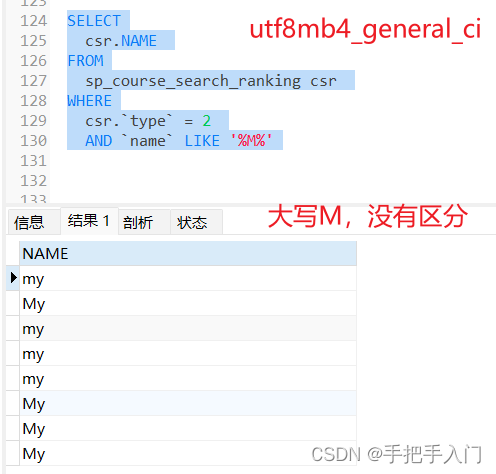
MySQL:区分大小写
查看MySQL版本 show variables; 1、查看 MySQL 当前的区分大小写设置: SHOW VARIABLES LIKE lower_case_table_names; 或者 show Variables like %table_names 2、更改大小写敏感设置: 在 MySQL 5.7 中,更改大小写敏感设置要求修改配置文件 …...

刷题笔记19——优势洗牌和去重保持字典序
摆出无比亲密的态度,装模作样地与对方套近乎,频繁地联系对方。这都说明他们并不相信自己得到了对方的信赖,若是互相信赖,便不会依赖亲密的感觉。在外人看来,反而显得冷淡。 ——尼采《人性的,太人性的》 ha…...
星际争霸之小霸王之小蜜蜂(十一)--杀杀杀
系列文章目录 星际争霸之小霸王之小蜜蜂(十)--鼠道 星际争霸之小霸王之小蜜蜂(九)--狂鼠之灾 星际争霸之小霸王之小蜜蜂(八)--蓝皮鼠和大脸猫 星际争霸之小霸王之小蜜蜂(七)--消失…...

腾讯云免费SSL证书申请流程_每年免费50个HTTPS证书
2023腾讯云免费SSL证书申请流程,一个腾讯云账号可以申请50张免费SSL证书,免费SSL证书为DV证书,仅支持单一域名,申请腾讯云免费SSL证书3分钟即可申请成功,免费SSL证书品牌为TrustAsia亚洲诚信,腾讯云百科分享…...

C#上位机开发目录
C#上位机序列1: 多线程(线程同步,事件触发,信号量,互斥锁,共享内存,消息队列) C#上位机序列2: 同步异步(async、await) C#上位机序列3: 流程控制(串行,并行,…...

网络通信基础
IP地址 使用ip地址来描述网络上一个设备所在的位置 端口号 区分一个主机上不同的程序,一个网络程序,在启动的时候,都需要绑定一个或者多个端口号,后续的通信过程都需要依赖端口号来进行展开的,mysql默认的端口号是3306 协议 描述了网络通信传输的数据的含义,表示一种约定,…...

框架分析(10)-SQLAlchemy
框架分析(10)-SQLAlchemy 专栏介绍SQLAlchemy特性分析ORM支持数据库适配器事务支持查询构建器数据库连接池事务管理器数据库迁移特性总结 优缺点优点强大的对象关系映射支持多种数据库灵活的查询语言自动管理数据库连接支持事务管理易于扩展和定制 缺点学…...
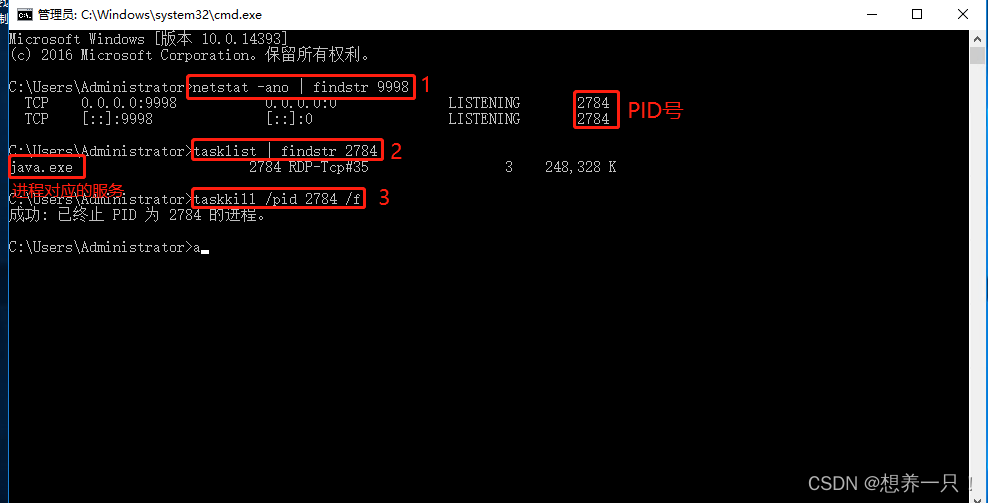
Linux/Windows中根据端口号关闭进程及关闭Java进程
目录 Linux 根据端口号关闭进程 关闭Java服务进程 Windows 根据端口号关闭进程 Linux 根据端口号关闭进程 第一步:根据端口号查询进程PID,可使用如下命令 netstat -anp | grep 8088(以8088端口号为例) 第二步:…...
基于springboot实现了后台定时统计数据报表并将数据生成excel文件作为附件,然后通过邮件发送通知的功能
概述 本例子基于springboot实现了后台定时统计数据报表并将数据生成excel文件作为附件,然后通过邮件发送通知的功能。 详细 一、准备工作 1、首先注册两个邮箱,一个发送邮箱,一个接收邮箱。 2、发送邮箱开启IMAP/SMTP/POP3服务,…...
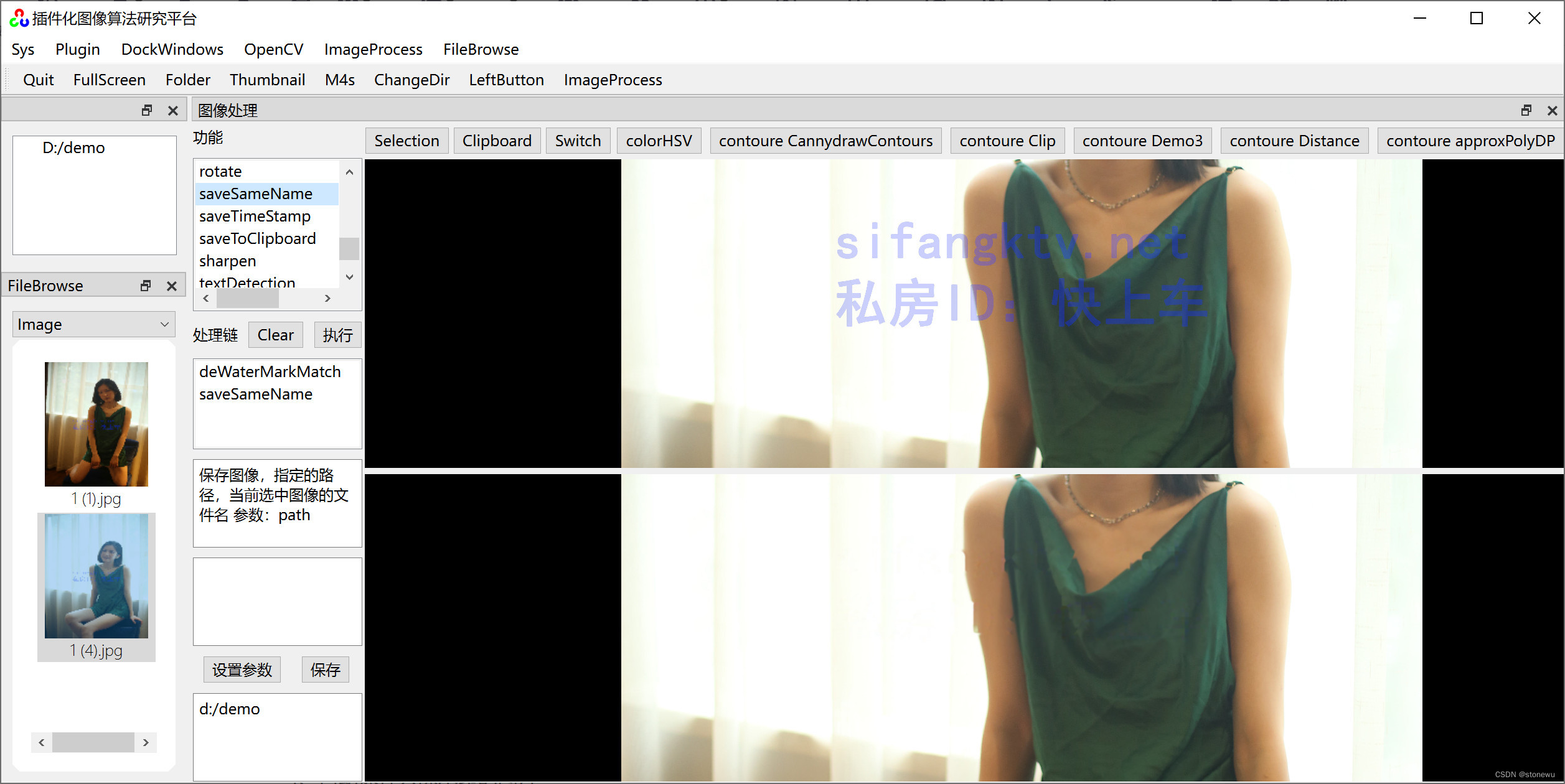
opencv 提取选中区域内指定hsv颜色的水印
基于《QT 插件化图像算法研究平台》做的功能插件。提取选中区域内指定hsv颜色的水印。 《QT 插件化图像算法研究平台》有个HSV COLOR PICK功能,可以很直观、方便地分析出水印 的hsv颜色,比如, 蓝色:100,180,0,255,100,255。 然后利用 opencv …...

如何理解张量、张量索引、切片、张量维度变换
Tensor 张量 Tensor,中文翻译“张量”,是一种特殊的数据结构,与数组和矩阵非常相似。在 PyTorch 中,使用张量对模型的输入和输出以及模型的参数进行编码。 Tensor 是一个 Python Class。PyTorch 官方文档中定义“Tensor࿰…...
基于SpringBoot的汽车租赁系统
基于SpringBootVue的汽车租赁系统,前后端分离 开发语言:Java数据库:MySQL技术:SpringBoot、Vue、Mybaits Plus、ELementUI工具:IDEA/Ecilpse、Navicat、Maven 角色:管理员、业务员、用户 管理员 用户管理…...

怎么做手机App测试?app测试详细流程和方法介绍
APP测试 1、手机APP测试怎么做? 手机APP测试,主要针对的是android和ios两大主流操作系统,主要考虑的就是功能性、兼容性、稳定性、易用性(也就是人机交互)、性能。 手机APP测试前的准备: 1.使用同类型的…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...
