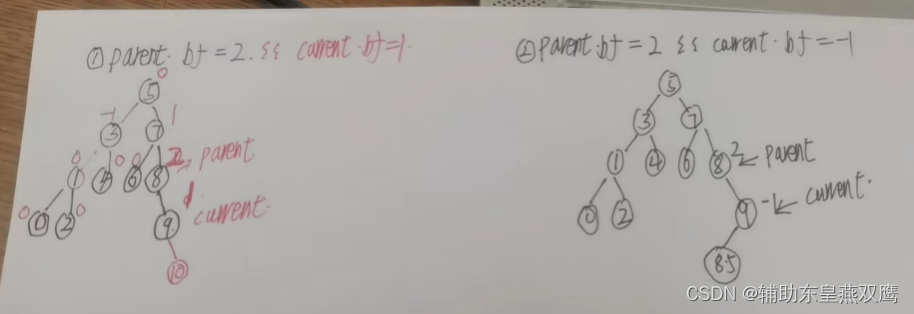高阶数据结构-----三种平衡树的实现以及原理(未完成)
TreeMap和TreeSet的底层实现原理就是红黑树
一)AVL树:
1)必须是一棵搜索树:前提是二叉树,任取一个节点,它的左孩子的Key小于父亲节点的Key小于右孩子节点的Key,中序遍历是有序的,按照Key的大小进行排列,高度平衡的二叉搜索树,他的左右子树都是二叉搜索树
AB C 甲 乙 丙 丁我们在这里面得出一个结论: Key(甲)<Key(B)<Key(乙)<Key(A)<Key(丙)<Key(C)<Key(丁)
2)必须是一颗平衡树:任意树中的节点,要求结点左子树的高度和结点右子树的高度差的绝对值不可以超过1,左右子树的高度差不能超过1;
平衡因子=左子树的高度-右子树的高度,我们在AVL树中任取一个节点,他的平衡因子只能是-1,1,0;
3)AVL树任意一颗以根节点的左右子树的高度差的绝对值不超过1,所以AVL树尽量保证左树和右树的高度是一致的,那么这个时候再次进行数据查找的时间复杂度就是O(logN)
4)当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过,(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度
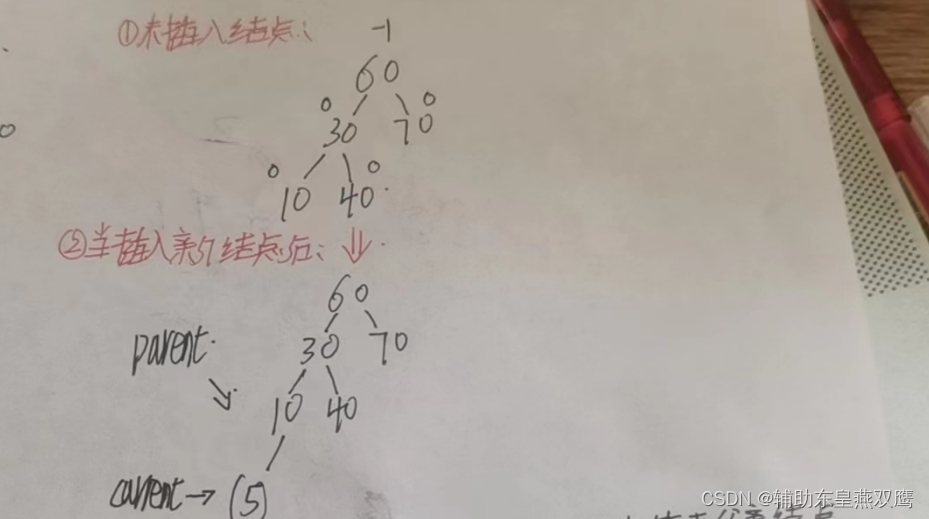
二)AVL树的查找与插入:如果插入失败了,那么只有一种情况那么就是当前我要插入的数值在原来的树中已经有了
随着节点的插入,导致了平衡因子发生了变化,所以我们要进行平衡因子的调节
1)如图所示,在上面这张图中当我们想要插入10这个节点的时候,parent此时指向的是9这个节点,此时10插入到了9的右子树,那么9的平衡因子++,此时parent的平衡因子是1,但是只能证明当前这棵树已经平衡了,还是需要进行向上调整
2)此时如果插入的数据是8.5,那么此时插入到的位置是9的左边,此时parent的平衡因子是-1,此时也是只能证明当前这棵树平衡了,还是需要继续向上调整的;
3)但是如果此时我们进行插入的数据是7.5,那么此时parent节点指向8这个位置,成功插入7.5这个数据之后发现parent的平衡因子变成0,此时就不需要向上调整了
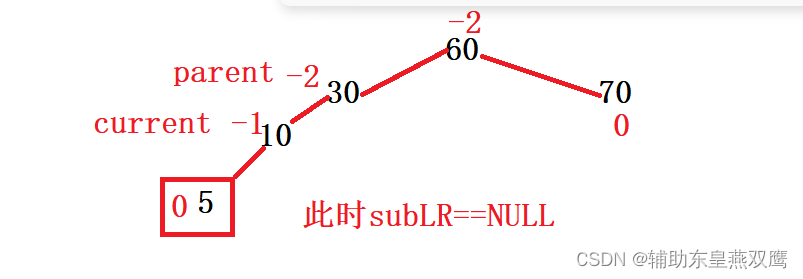
当parent.bf==2的时候,说当前这棵树已经不平衡了,说明此时右树高,说明要降低右树的高度,增加左树的高度,所以要进行旋转
当parent.bf==-2的时候,说当前这棵树已经不平衡了,说明此时左树高,说明要降低左树的高度,增加右树的高度,所以要进行旋转
左旋说明右树高,右旋说明左树高
一)parent节点的平衡因子是2,current节点存储的平衡因子是1:
二)parent结点的平衡因子是2,current的节点的平衡因子是-1;
三)parent结点存储的平衡因子是-2,current存储结点的平衡因子是-1;
1)这个旋转也叫做右单旋,除了修改指针的指向还有修改平衡因子,右单旋就是自己变成左孩子的右孩子
2)但是代码写到这里面还是存在着一定问题,可能当前的parent是上面某一棵树的左子树,也有可能是某一棵树的右子树
3)最后修改各个节点的平衡因子
4)但是上面的所有情况都考虑得比较不错了,但是最终的代码还是存在着一定的瑕疵
四)parent存储结点的平衡因子是-2,current存储结点的平衡因子是1;
右单旋:(新节点插入较高左子树的右侧)
左旋——自己变为右孩子的左孩子;右旋——自己变为左孩子的右孩子
在上面的代码中,我们就成功地进行了右旋;
左单旋:新节点插入较高右子树的右侧
左右双旋:新节点插入到较高左子树的右侧
解决方案:先针对parent的左子树进行左旋,再根据parent结点进行右旋,再进行更新平衡因子的变化
右左双旋:新节点插入到较高右子树的左侧
验证AVL树:中序遍历有序况且是平衡二叉树
相关文章:

高阶数据结构-----三种平衡树的实现以及原理(未完成)
TreeMap和TreeSet的底层实现原理就是红黑树 一)AVL树: 1)必须是一棵搜索树:前提是二叉树,任取一个节点,它的左孩子的Key小于父亲节点的Key小于右孩子节点的Key,中序遍历是有序的,按照Key的大小进行排列,高度平衡的二叉…...

北斗高精度组合导航终端
UWB(Ultra-Wideband)、卫星定位(GNSS),以及IMU(Inertial Measurement Unit)的组合定位系统结合了多种传感器和定位技术,以提供高精度、高可靠性的位置估计。这种组合定位系统在各种应…...

低代码平台是否能替代电子表格?
在计算机技术普及之前,会计、助理或者是销售人员,都需要用纸和笔来记录和维护每一笔交易。计算机技术兴起之后,一项技术发明——电子表格的出现改变了低效的状况。电子表格的第一个版本出现在1977年,一个名为“VisiCalc”的程序。…...

qt多个信号如何关联一并处理
主要方法: 首先,需要创建一个包含自定义信号和槽的Qt类。假设要创建一个名为MyObject的类,并在其中定义一个自定义信号和一个槽。这个类的头文件可能如下所示: #ifndef MYOBJECT_H #define MYOBJECT_H#include <QObject>c…...
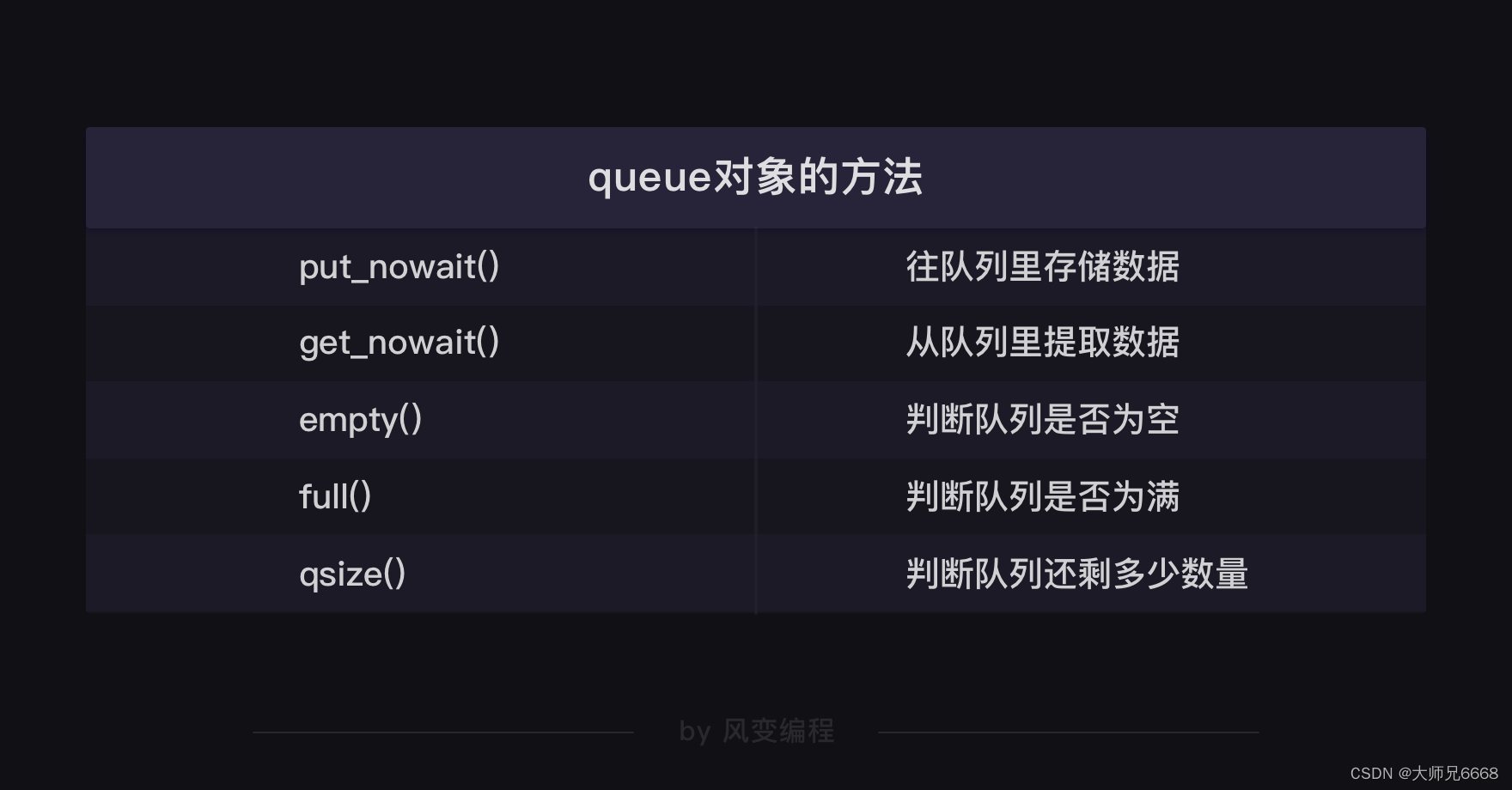
【python爬虫】12.建立你的爬虫大军
文章目录 前言协程是什么多协程的用法gevent库queue模块 拓展复习复习 前言 照旧来回顾上一关的知识点!上一关我们学习如何将爬虫的结果发送邮件,和定时执行爬虫。 关于邮件,它是这样一种流程: 我们要用到的模块是smtplib和emai…...

2023数学建模国赛C题思路--蔬菜类商品的自动定价与补货决策
C 题 蔬菜类商品的自动定价与补货决策 在生鲜商超中,一般蔬菜类商品的保鲜期都比较短,且品相随销售时间的增加而变差, 大部分品种如当日未售出,隔日就无法再售。因此,商超通常会根据各商品的历史销售和需 求情况每天进…...

vue2与vue3的使用区别
1. 脚手架创建项目的区别: vue2: vue init webpack “项目名称”vue3: vue create “项目名称” 或者vue3一般与vite结合使用: npm create vitelatest yarn create vite2. template中结构 vue2: template下只有一个元素节点 <template><div><div…...
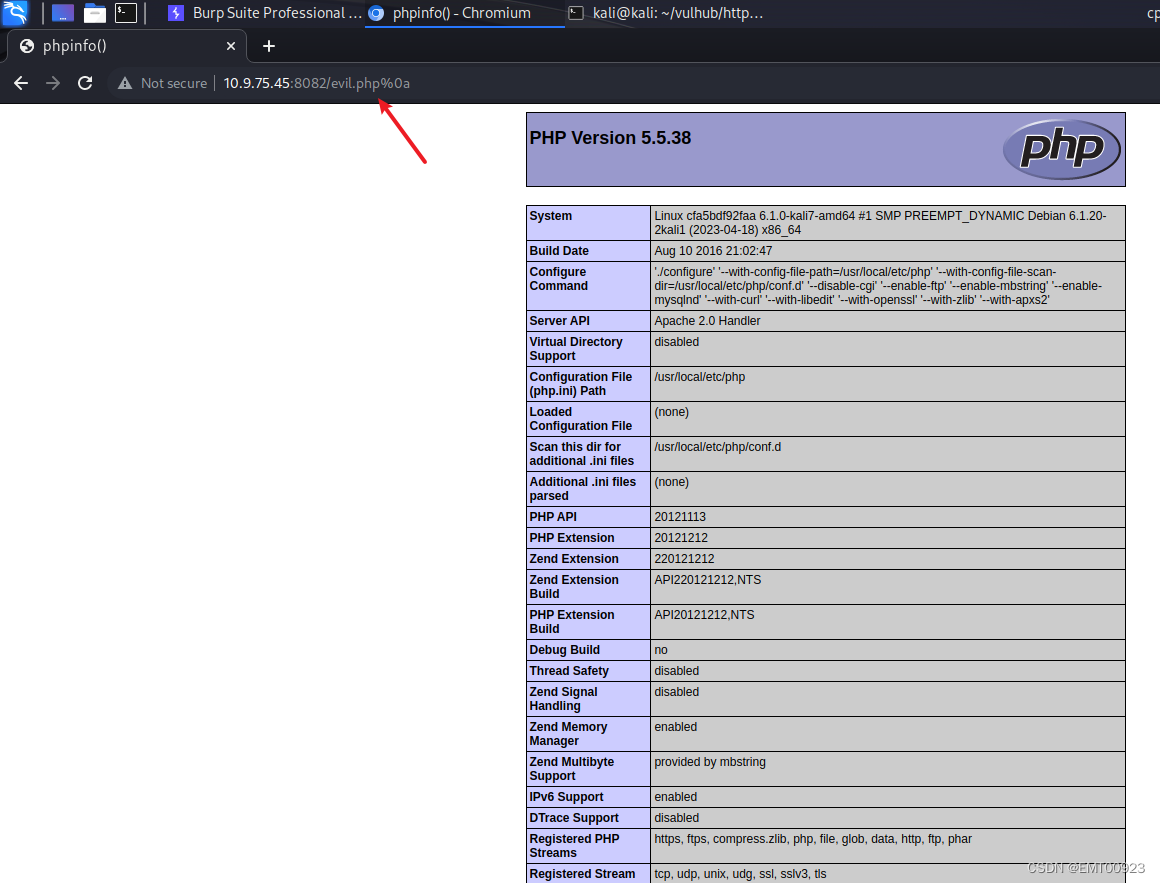
Apache httpd漏洞复现
文章目录 未知后缀名解析漏洞多后缀名解析漏洞启动环境漏洞复现 换行解析漏洞启动环境漏洞复现 未知后缀名解析漏洞 该漏洞与Apache、php版本无关,属于用户配置不当造成的解析漏洞。在有多个后缀的情况下,只要一个文件含有.php后缀的文件即将被识别成PHP…...
【漏洞复现】时空智友企业流程化管控系统文件上传
漏洞描述 通过时空智友该系统,可让企业实现流程的自动化、协同上提升、数据得洞察及决策得优化,来提高工作效率、管理水平及企业的竞争力。时空智友企业流程化 formservice接口处存有任意文件上传漏洞,未经认证得攻击者可利用此接口上传后门程序,可导致服务器失陷。 免责…...
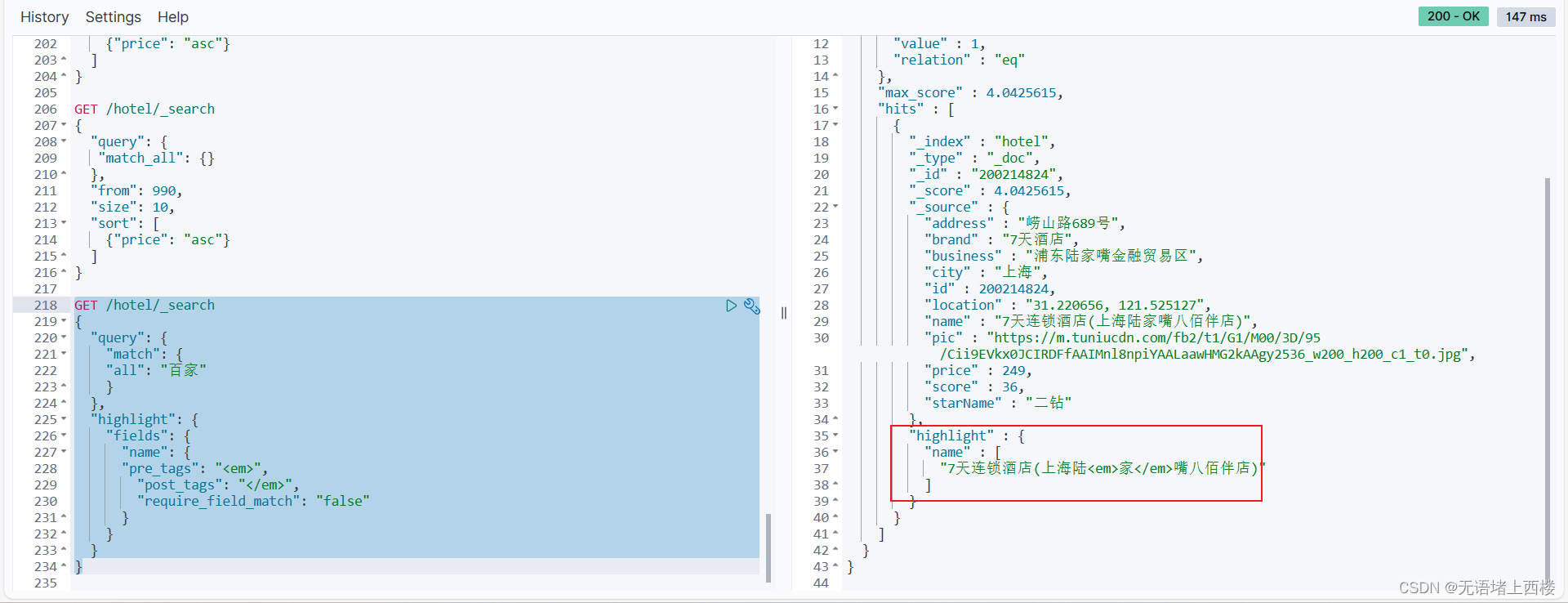
elasticsearch的DSL查询文档
DSL查询分类 查询所有:查询出所有数据,一般测试用。例如:match_all 全文检索(full text)查询:利用分词器对用户输入内容分词,然后去倒排索引库中匹配。例如: match_query multi_ma…...
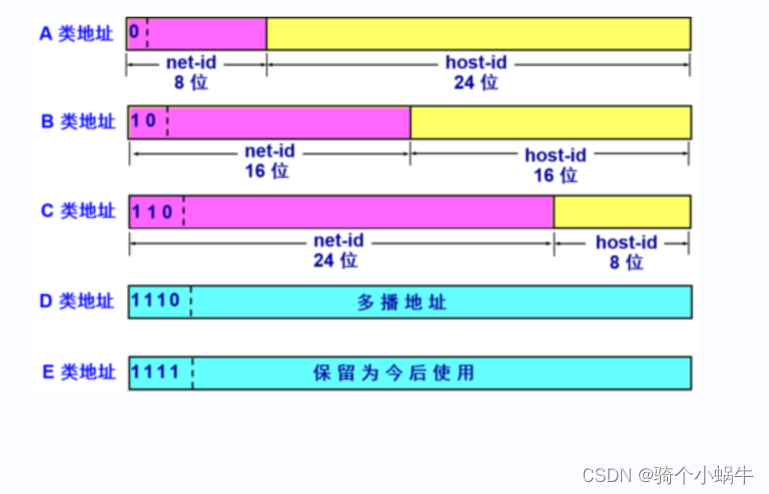
IP地址、子网掩码、网络地址、广播地址、IP网段
文章目录 IP地址IP地址分类子网掩码网络地址广播地址IP网段 本文主要讨论iPv4地址。 IP地址 实际的 IP 地址是一串32 比特的数字,按照 8 比特(1 字节)为一组分成 4 组,分别用十进制表示然后再用圆点隔开,这就是我们平…...
ffmpeg-android studio创建jni项目
一、创建native项目 1.1、选择Native C 1.2、命名项目名称 1.3、选择C标准 1.4、项目结构 1.5、app的build.gradle plugins {id com.android.application }android {compileSdk 32defaultConfig {applicationId "com.anniljing.ffmpegnative"minSdk 25targetSdk 32…...

智慧公厕是将数据、技术、业务深度融合的公共厕所敏捷化“操作系统”
文明社会的进步离不开公共设施的不断创新和提升。而在这些公共设施中,公共厕所一直是一个备受关注和改善的领域。近年来,随着智慧城市建设的推进,智慧公厕成为了城市管理的重要一环。智慧公厕不仅仅是为公众提供方便和舒适的便利设施…...
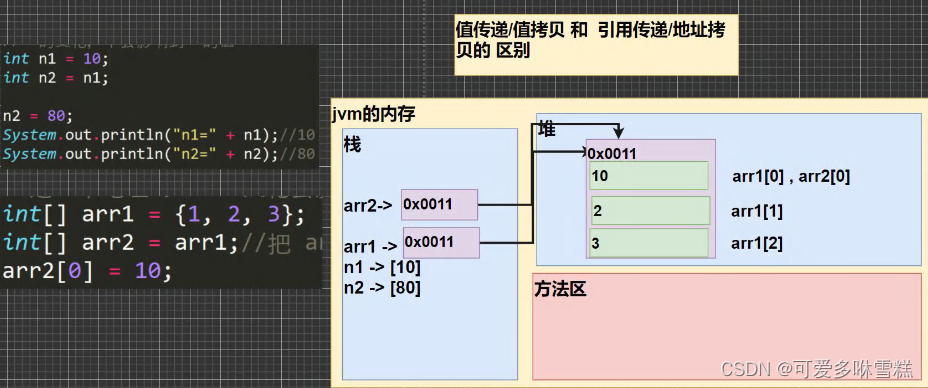
JVM中JAVA对象和数组内存布局
对象 数组 在Java中,所有的对象都是一种特殊的数组,它们的元素可以是基本数据类型、其他对象引用或者其他任何类型。Java对象和数组的内存布局包含以下部分: 1.对象头(Object Header) 每个Java对象都有一个对象头&am…...

【2023年数学建模国赛】赛题发布
2023数学建模国赛赛题已经发布啦,距离赛题发布已经过去三个小时了,大家是否已经确定题目呢?学姐后续会持续更新赛题思路与代码~...

Java HashMap源码学习
Java HashMap源码学习 基本使用 包含创建,添加,删除,迭代,打印 val map java.util.HashMap<Int, Int>() map.put(1, 2) map.put(2, 2) map.put(3, 2) map.remove(1) map.forEach {println("it.key${it.key}, it.va…...

Gin中用于追踪用户的状态的方法?!!!
Gin中的Cookie和Session的用法 文章目录 Gin中的Cookie和Session的用法介绍Cookie代码演示 Session代码展示 介绍 cookie 和 session 是 Web 开发中常用的两种技术,主要用于跟踪用户的状态信息。 Cookie func (c *Context) Cookie(name string, value string, max…...

HTTP代理与HTTPS代理在工作流程上有哪些区别
HTTP代理和HTTPS代理都是常见的代理技术,可以实现隐藏客户端IP地址、突破网络封锁、加速网站访问、过滤网络内容等功能。本文将介绍HTTP代理和HTTPS代理在工作流程上的区别。 HTTP代理的工作流程 客户端向代理服务器发送HTTP请求 当客户端需要访问某个网站时&#x…...

Docker从认识到实践再到底层原理(二-2)|Namespace+cgroups
前言 那么这里博主先安利一些干货满满的专栏了! 首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。 高质量博客汇总 然后就是博主最近最花时间的一个专栏…...

算法的概述
算法分析: 解决同一问题的算法可以有多种。 我们希望从中选出最优的算法,效率高或者存储空间小。为此,需要对算法进行评估,分析。 通常考虑两个度量: 1、 时间复杂度:算法运行时需要的总步数,…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...