算法专题:前缀和
文章目录
- Acwing:前缀和示例
- 2845.统计趣味子数组的数目
- 思路
- 容易理解的写法:前缀和+两层循环
- 存在问题:超时
- 优化写法:两数之和思路,转换为哈希表
前缀和,就是求数组中某一段的所有元素的和。
求子数组中某一段数字的元素和,只需要转换成两个数字的差值就可以了。
注意:
- 只能求连续某一段区间的元素和
- 一般来说前缀和需要在前面加一个0,因为表示成两个数字的差的话,如果前面不加0,带有第一个数字的元素和无法表示成差值,例如下图

Acwing:前缀和示例
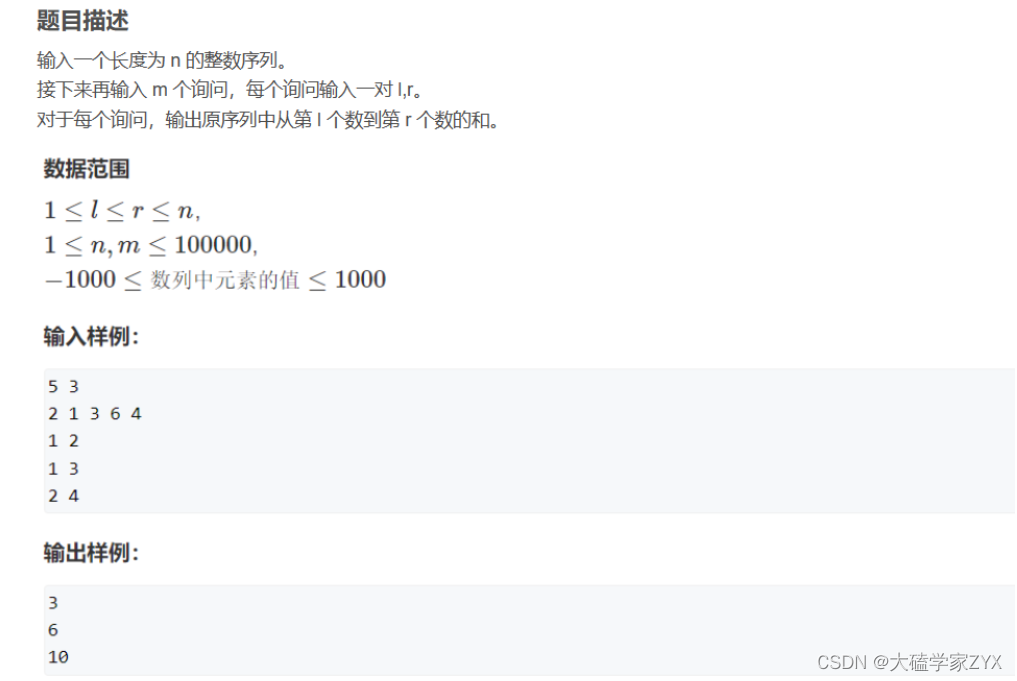
- 前缀和注意:需要在最前面加上一个0,所以前缀和数组大小是nums.size()+1
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;int main()
{int n, m, l, r;scanf("%d%d", &n, &m);int a[n], sum[n + 1]; // s设置为n+1是为了后面计算方便for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);sum[0] = 0;for (int i = 0; i < n; i ++ ) sum[i + 1] = sum[i] + a[i];while (m -- ) {scanf("%d%d", &l, &r);printf("%d\n", sum[r] - sum[l - 1]); // 这里的l和r是1~n范围}return 0;
}- 读入两个整数
n和m。n是数组a的大小,m是查询的数量。 - 定义数组
a和sum。a用于存储输入的整数序列,sum用于存储前缀和。 - 初始化
sum[0]为0。 - 使用循环计算
sum数组,其中sum[i]存储了数组a的前i个元素的和。 - 循环进行
m次查询,每次查询读入两个整数l和r,然后输出区间[l, r]的和。这个和可以通过sum[r] - sum[l - 1]很快得到。注意,这里的l和r是1-based,也就是从1开始的,而数组索引是0-based。所以可以直接用sum[r]-sum[l-1],因为r本身已经是对应的下标+1了。
代码示例中的 sum[r] - sum[l - 1] 是核心点。为了理解它,考虑下面的例子:
a: 2 3 4 5
sum: 0 2 5 9 14
为了得到 [2, 4] (这里的下标r和l是从1开始的)子区间和 (即 3 + 4 + 5),我们可以使用 sum[4] - sum[2 - 1],结果为 12。
2845.统计趣味子数组的数目
给你一个下标从 0 开始的整数数组 nums ,以及整数 modulo 和整数 k 。
请你找出并统计数组中 趣味子数组 的数目。
如果 子数组 nums[l..r] 满足下述条件,则称其为 趣味子数组 :
- 在范围
[l, r]内,设cnt为满足nums[i] % modulo == k的索引i的数量。并且cnt % modulo == k。
以整数形式表示并返回趣味子数组的数目。
**注意:**子数组是数组中的一个连续非空的元素序列。
示例 1:
输入:nums = [3,2,4], modulo = 2, k = 1
输出:3
解释:在这个示例中,趣味子数组分别是:
子数组 nums[0..0] ,也就是 [3] 。
- 在范围 [0, 0] 内,只存在 1 个下标 i = 0 满足 nums[i] % modulo == k 。
- 因此 cnt = 1 ,且 cnt % modulo == k 。
子数组 nums[0..1] ,也就是 [3,2] 。
- 在范围 [0, 1] 内,只存在 1 个下标 i = 0 满足 nums[i] % modulo == k 。
- 因此 cnt = 1 ,且 cnt % modulo == k 。
子数组 nums[0..2] ,也就是 [3,2,4] 。
- 在范围 [0, 2] 内,只存在 1 个下标 i = 0 满足 nums[i] % modulo == k 。
- 因此 cnt = 1 ,且 cnt % modulo == k 。
可以证明不存在其他趣味子数组。因此,答案为 3 。
示例 2:
输入:nums = [3,1,9,6], modulo = 3, k = 0
输出:2
解释:在这个示例中,趣味子数组分别是:
子数组 nums[0..3] ,也就是 [3,1,9,6] 。
- 在范围 [0, 3] 内,只存在 3 个下标 i = 0, 2, 3 满足 nums[i] % modulo == k 。
- 因此 cnt = 3 ,且 cnt % modulo == k 。
子数组 nums[1..1] ,也就是 [1] 。
- 在范围 [1, 1] 内,不存在下标满足 nums[i] % modulo == k 。
- 因此 cnt = 0 ,且 cnt % modulo == k 。
可以证明不存在其他趣味子数组,因此答案为 2 。
提示:
1 <= nums.length <= 10^51 <= nums[i] <= 10^91 <= modulo <= 10^90 <= k < modulo
思路
首先思路就是运用前缀和,单独开一个x数组遍历所有的nums[i],满足条件计数为1,不满足条件计数为0。
这样的话,子数组[l,r]内满足条件的数字个数,直接就是子数组对应的x数组区间的和!
容易理解的写法:前缀和+两层循环
#include <vector>class Solution {
public:long countInterestingSubarrays(std::vector<int>& nums, int modulo, int k) {int n = nums.size();// 创建一个数组x来标记哪些数字模`modulo`后等于kstd::vector<int> x(n, 0);// 创建一个前缀和数组std::vector<int> sum(n + 1, 0);// ----------- 前缀和计算开始 -----------for (int i = 0; i < n; ++i) {// 如果当前数字模`modulo`后等于k,则在x数组中的对应位置标记为1if (nums[i] % modulo == k) x[i] = 1;// 计算前缀和:当前位置的前缀和等于上一个位置的前缀和加上x数组中的当前值sum[i + 1] = sum[i] + x[i];}// ----------- 前缀和计算结束 -----------// 初始化答案为0long ans = 0;// 使用两重循环来检查所有可能的子数组和for (int l = 0; l < n; ++l) { // 子数组的开始位置for (int r = l + 1; r <= n; ++r) { // 子数组的结束位置// 如果子数组的和模`modulo`后等于k,则增加答案的值if ((sum[r] - sum[l]) % modulo == k) ans++;}}// 返回答案return ans;}
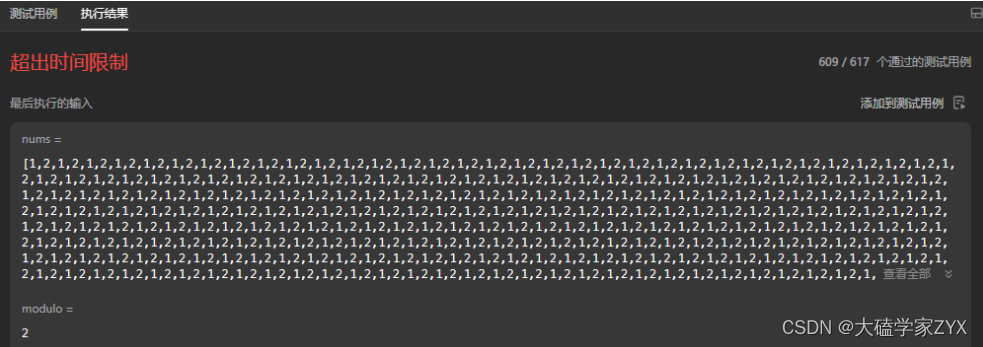
};存在问题:超时
这种写法因为子数组两边都不定,会超时,时间复杂度是O(n^2)。
优化写法:两数之和思路,转换为哈希表
因为上面写法出现了超时,我们可以用类似 两数之和 的套路,来优化时间复杂度,用map来减少一层循环。
-
两数之和的优化方法是,遍历到nums[i]的时候,先看看target-nums[i]是不是已经在map里面了。如果在直接返回,不在就加到map里面,继续遍历数字。遍历完了数组之后一定会收集所有的相加=目标和的两数组合。
-
本题的优化方法是,我们遍历sum[r]的时候,找满足sum[r] - sum[l]) % modulo == k条件的sum[l]是不是已经在哈希表里面了。哈希表map的作用是存放已经枚举过的sum。
#include <vector>
#include <unordered_map>class Solution {
public:long countInterestingSubarrays(std::vector<int>& nums, int modulo, int k) {int n = nums.size();// x是原始数组,sum是前缀和数组std::vector<int> x(n, 0);std::vector<int> sum(n + 1, 0);// 使用unordered_map存储各个余数的位置数量std::unordered_map<int, int> cnt;cnt[0] = 1;long ans = 0;for (int i = 0; i < n; ++i) {if (nums[i] % modulo == k) x[i] = 1;// 计算前缀和sum[i + 1] = (sum[i] + x[i]) % modulo;int r = sum[i + 1];// 此处的索引就是在找满足条件的sum[l],r就是之前版本的sum[r]//需要满足的式子是(sum[r] - sum[l]) % modulo == k//这里+modulo的目的是为了防止r-k是负数,+m再取余,结果还是0不会影响ans += cnt[(r - k + modulo) % modulo];// 更新哈希表中的计数,这里是在更新sum[r]进哈希表(对应之前版本)cnt[r]++;}return ans;}
};相关文章:

算法专题:前缀和
文章目录 Acwing:前缀和示例2845.统计趣味子数组的数目思路容易理解的写法:前缀和两层循环存在问题:超时 优化写法:两数之和思路,转换为哈希表 前缀和,就是求数组中某一段的所有元素的和。 求子数组中某一…...

bs4库爬取天气预报
Python不仅用于网站开发,数据分析,图像处理,也常用于爬虫技术方向,最近学习了解下,爬虫技术入门一般先使用bs4库,爬取天气预报简单尝试下。 第一步:首先选定目标网站地址 网上查询,…...

l8-d8 TCP并发实现
一、TCP多进程并发 1.地址快速重用 先退出服务端,后退出客户端,则服务端会出现以下错误: 地址仍在使用中 解决方法: /*地址快速重用*/ int flag1,len sizeof (int); if ( setsockopt(fd, SOL_SOCKET, SO_REUSEADDR, &a…...

编写中间件以用于 Express 应用程序
概述 中间件函数能够访问请求对象 (req)、响应对象 (res) 以及应用程序的请求/响应循环中的下一个中间件函数。下一个中间件函数通常由名为 next 的变量来表示。 中间件函数可以执行以下任务: 执行任何代码。对请求和响应对象进行更改。结束请求/响应循环。调用堆…...

【2023年数学建模国赛】D题解题思路
2023年数学建模国赛D题解题思路 为了解决问题1、问题2和问题3,我们可以采用动态规划方法来制定生产计划,考虑了不确定性因素和多种可能情况的预案集。首先,我们需要定义一些变量和符号: T T T:总的养殖周期࿰…...

python爬虫之正则表达式学习
网络安全离不开脚本和工具的开发,python很多又需要正则表达式。 这是一个很好的学习正则表达式的项目 https://github.com/ziishaned/learn-regex/blob/master/translations/README-cn.md 基本匹配 正则表达式其实就是在执行搜索时的格式,它由一些字…...

智慧能源方案:TSINGSEE青犀AI算法中台在能源行业的应用
一、方案背景 互联网、物联网、人工智能等新一代信息技术引领新一轮产业革命,加快能源革命步伐。尤其是随着人工智能技术的不断发展,AI智能检测与识别技术在能源行业的应用也越来越广泛。与此同时,国家出台多项政策,将智慧能源纳…...

达梦数据库awr报告收集
1、找出快照点snap_id与时间的对应关系 SYS.WRM$_SNAPSHOT表中记录了快照点snap_id与时间的对应关系 例如如下语句可以得出2023-09-04这一天各个时间点对应的快照点snap_id select snap_id,end_interval_time from SYS.WRM$_SNAPSHOT where end_interval_time between to…...

c语言练习43:深入理解strcmp
深入理解strcmp strcmp的主要功能是用来比较两个字符串 模拟实现strcmp 比较两个字符串对应位置上的大小 按字典序进行比较 例如: 输入:abc abc 输出:0 输入:abc ab 输出:>0的数 输入:ab abc …...

NUC980webServer开发
目录 1.RTL8189FTV驱动移植 2.wifi配置工具hostapd移植 1.openssl-1.0.2r交叉编译 2.libnl-3.2.25.tar.gz交叉编译 3.hostapd-2.9.tar.gz交叉编译 4.移植相关工具到开发板 1.RTL8189FTV驱动移植 1. 把驱动文件源码放在linux源码的drivers/net/wireless/realtek/rtlwifi/目录…...

驱动开发--day2
实现三盏灯的控制,编写应用程序测试 head.h #ifndef __HEAD_H__ #define __HEAD_H__#define LED1_MODER 0X50006000 #define LED1_ODR 0X50006014 #define LED1_RCC 0X50000A28#define LED2_MODER 0X50007000 #define LED2_ODR 0X50007014#endif mychrdev.c #inc…...
用户促活留存新方式——在APP中嵌入小游戏
随着APP同类产品的不断出现,APP开发者们面临着激烈的竞争,很多APP下载后被新的APP取代,获客成本越来越高。同时开发者还会面临用户粘性差、忠诚度低、用完即走、留存困难,商业化价值被大大缩减。 在APP中植入小游戏来提高用户活跃…...

MySQL 8.0.34(x64)安装笔记
一、背景 从MySQL 5.6到5.7,再到8.0,版本的跳跃不可谓不大。安装、配置的差别也不可谓不大,特此备忘。 二、过程 (1)获取MySQL 8.0社区版(MySQL Community Server) 从 官网 字样 “MySQL …...

物流供应商实现供应链自动化的3种方法
当前影响供应链的全球性问题(如新冠肺炎疫情)正在推动许多物流供应商重新评估和简化其流程。运输协调中的摩擦只会加剧供应商无法控制的现有延误和风险。值得庆幸的是,供应链专业人员可以通过端到端的供应链自动化消除延迟,简化与合作伙伴的沟通…...

Mysql更新时间列只改日期为指定日期不更改时间
场景 Mysql分表后同结构不同名称表之间复制数据以及Update语句只更新日期加减不更改时间: Mysql分表后同结构不同名称表之间复制数据以及Update语句只更新日期加减不更改时间_霸道流氓气质的博客-CSDN博客 上面通过如下方式实现日期列增加指定天数。 UPDATE bus…...
实时测试工具 Visual Studio 扩展 NCrunch 4.18 Crack
NCrunch Visual Studio 扩展 .NET 的终极实时测试工具 在编码时查看实时测试结果和内联指标。 下载v4.18 发布于 2023 年 7 月 17 日 跳过视频至: 代码覆盖率 指标 分布式处理 配置 发动机模式 Visual Studio 自动并发测试 NCrunch 是一个完全自动化的测试扩展&a…...

Neo4j 基本语法
一、基本语法 1、新建节点 (1)基本语法: () 代表节点 示例: CREATE (u:User {uid:970939424 }) // 节点类型为User,属性值为uid970939424CREATE (u:Round {rid:7194842697444819113 }) // 节点类型为Rou…...

docker常见面试题
1.什么是docker docker是一个容器化平台,类似于一个集装箱,集装箱与集装箱之间互不影响,docker平台就是一个软件集装箱平台,我们可以构建应用程序,将其所有的依赖打包到一个容器中,然后就很方便的可以在其…...
静态路由:配置和使用详解
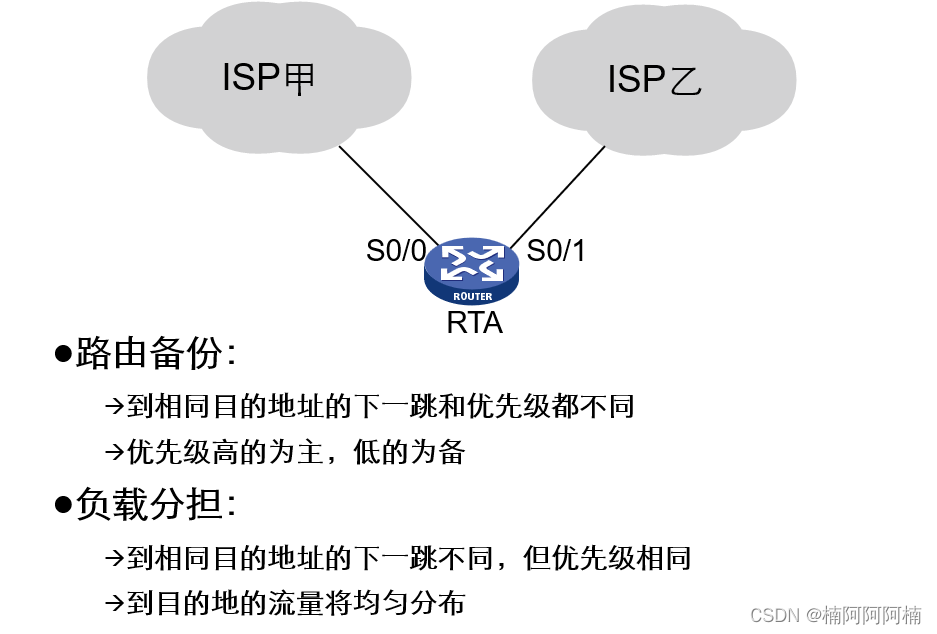
文章目录 一、静态路由的配置和使用详解1. 配置要点1.1 点到点接口配置1.2 以太网接口配置 2. 默认路由3. 静态路由的配置命令4. 静态路由实现路由备份和负载分担 二、静态路由的优先级和比较1. 静态路由的优先级设置2. 静态路由与动态路由的比较2.1 静态路由优缺点2.2 动态路由…...

玩转Mysql系列 - 第15篇:详解视图
这是Mysql系列第15篇。 环境:mysql5.7.25,cmd命令中进行演示。 需求背景 电商公司领导说:给我统计一下:当月订单总金额、订单量、男女订单占比等信息,我们啪啦啪啦写了一堆很复杂的sql,然后发给领导。 …...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...
