每日刷题|回溯法解决全排列问题

食用指南:本文为作者刷题中认为有必要记录的题目
前置知识:回溯法经典问题之组合
♈️今日夜电波:爱人错过—告五人
1:11 ━━━━━━️💟──────── 4:52
🔄 ◀️ ⏸ ▶️ ☰
💗关注👍点赞🙌收藏您的每一次鼓励都是对我莫大的支持😍
目录
回溯法的理解
💮 一、全排列
🌺二、全排列II
回溯法的理解
本文参考了一位大佬的题解,详细的介绍了回溯法:链接
上一篇刷题文: 回溯法经典问题之子集
记住一句话:for循环横向遍历,递归纵向遍历,回溯不断调整结果集。 这句话将从始至终贯穿我们对于以上问题的回溯解决办法。
💮 一、全排列
题目链接:46. 全排列
题目描述:
给定一个不含重复数字的数组
nums,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1] 输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1] 输出:[[1]]
提示:
1 <= nums.length <= 6-10 <= nums[i] <= 10nums中的所有整数 互不相同
本题思路:
首先:采用经典的“回溯三部曲”:
1、定义两个全局变量,一个用来存放符合条件单一结果(path),一个用来存放符合条件结果的集合(result)。
2、回溯的主体,回溯终止条件。path保存一组数据,每次遍历到叶子节点,再插入到result中,并且回溯到上一个节点。
3、单层搜索的过程。for循环用来横向遍历,递归的过程是纵向遍历。
根据题意我们做出一定的改动:
我们额外定义一个bool类型的used用于确定每一个节点是否使用过,以此来解决重复插入的问题,并且也可以通过used对应的位置是否为false来确定是否进行后续操作。一句话概括就是:只有当used[i]==0时才去进行后续操作。
一图让你了解~以{1,2,3}为例

class Solution {
private:
vector<int> path;
vector<vector<int>> result;void trackback(vector<int>& nums,vector<bool>& used)
{if(path.size()==nums.size()){result.push_back(path);}for(int i=0;i<nums.size();i++){if(used[i]!=1){path.push_back(nums[i]);used[i]=1;trackback(nums,used);used[i]=0;path.pop_back();}}
}
public:vector<vector<int>> permute(vector<int>& nums) {path.clear();result.clear();vector<bool> used;used.resize(nums.size());sort(nums.begin(),nums.end());trackback(nums,used);return result;}
};🌺二、全排列II
题目链接:47. 全排列 II
题目描述:
给定一个可包含重复数字的序列
nums,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2] 输出: [[1,1,2],[1,2,1],[2,1,1]]
示例 2:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
提示:
1 <= nums.length <= 8-10 <= nums[i] <= 10
本题思路:
本题实际上为上一题的拓展题目,基本上的思路跟上一题是的没什么区别的,但是由于此题中的元素是可以重复的,那我们就不能按照上一题只需要全部遍历一遍节点即可,在这里,我们需要加入剪枝操作,以此来解决重复选取问题。一句话概括就是:同一树枝上可以选取,但是同一树层上不可以选取!
即:添加这段判断语句{i>0&&nums[i-1]==nums[i]&&used[i-1]==0}来筛选重复的元素!
一图让你了解~以{1,1,2}为例
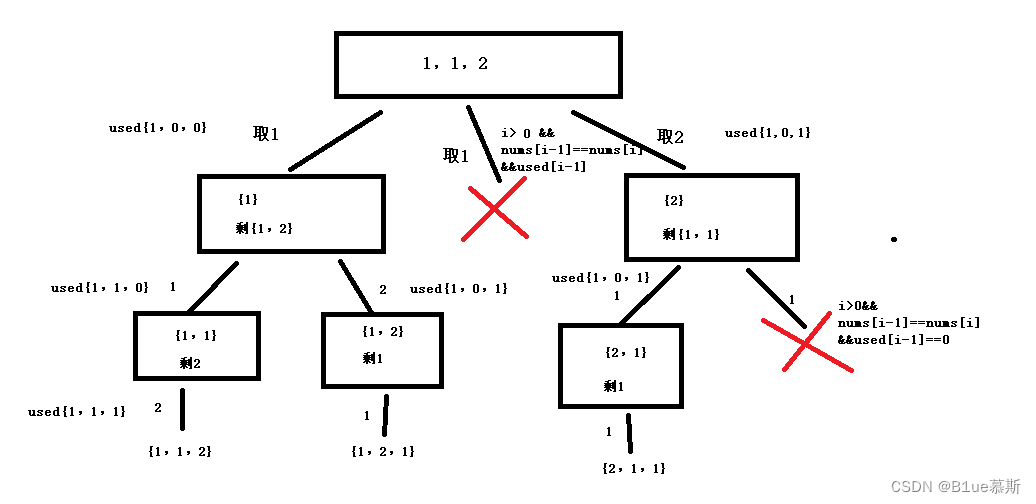
class Solution {
private:
vector<int> path;
vector<vector<int>> result;void trackback(vector<int>& nums,vector<bool>& used)
{if(path.size()==nums.size()){result.push_back(path);return;}for(int i=0;i<nums.size();i++){if(i>0&&nums[i-1]==nums[i]&&used[i-1]==0)continue;if (used[i] != 1){path.push_back(nums[i]);used[i] = 1;trackback(nums, used);used[i] = 0;path.pop_back();}}
}
public:vector<vector<int>> permuteUnique(vector<int>& nums) {path.clear();result.clear();vector<bool> used;used.resize(nums.size());sort(nums.begin(),nums.end());trackback(nums,used);return result;}
};感谢你耐心的看到这里ღ( ´・ᴗ・` )比心,如有哪里有错误请踢一脚作者o(╥﹏╥)o!

给个三连再走嘛~
相关文章:

每日刷题|回溯法解决全排列问题
食用指南:本文为作者刷题中认为有必要记录的题目 前置知识:回溯法经典问题之组合 ♈️今日夜电波:爱人错过—告五人 1:11 ━━━━━━️💟──────── 4:52 …...

10-JVM调优工具详解
上一篇:09-JVM垃圾收集底层算法实现 前置启动程序 事先启动一个web应用程序,用jps查看其进程id,接着用各种jdk自带命令优化应用 1.Jmap 此命令可以用来查看内存信息,实例个数以及占用内存大小 jmap -histo 14660 #查看历史…...
)
东方博易oj——3119 - 约瑟夫问题2(链表)
文章目录 题目题目描述输入输出样例输入 输出标签 AC代码 题目 题目描述 约瑟夫问题:有 n n n只猴子,按顺时针方向围成一圈选大王(编号从 1 1 1到 n &#…...
C++,day0907
#include <iostream>using namespace std; struct stu { private:int num; private:double score[32];public:void setNum(){cout <<"请输入学生人数:";cin >>num;}void input(){cout<<"请输入学生的成绩:"<<endl;for(int i…...

孤儿僵尸守护进程的简单理解
孤儿进程: 一个父进程退出,而它的一个或多个子进程还在运行,那么那些子进程将成为孤儿进程。孤儿进程将被init进程所收养,并由init进程对它们完成状态收集工作。 如何模仿一个孤儿进程: 答案是: kill 父…...

学习笔记——Java入门第一季
1.1 Java的介绍与前景 Java语言最早期的制作者:James Gosling(詹姆斯高斯林) 1995年5月23日,Sun Microsystems公司宣布Java语言诞生。 1.2 Java的特性与版本 跨平台 开源(开放源代码) Java代码ÿ…...
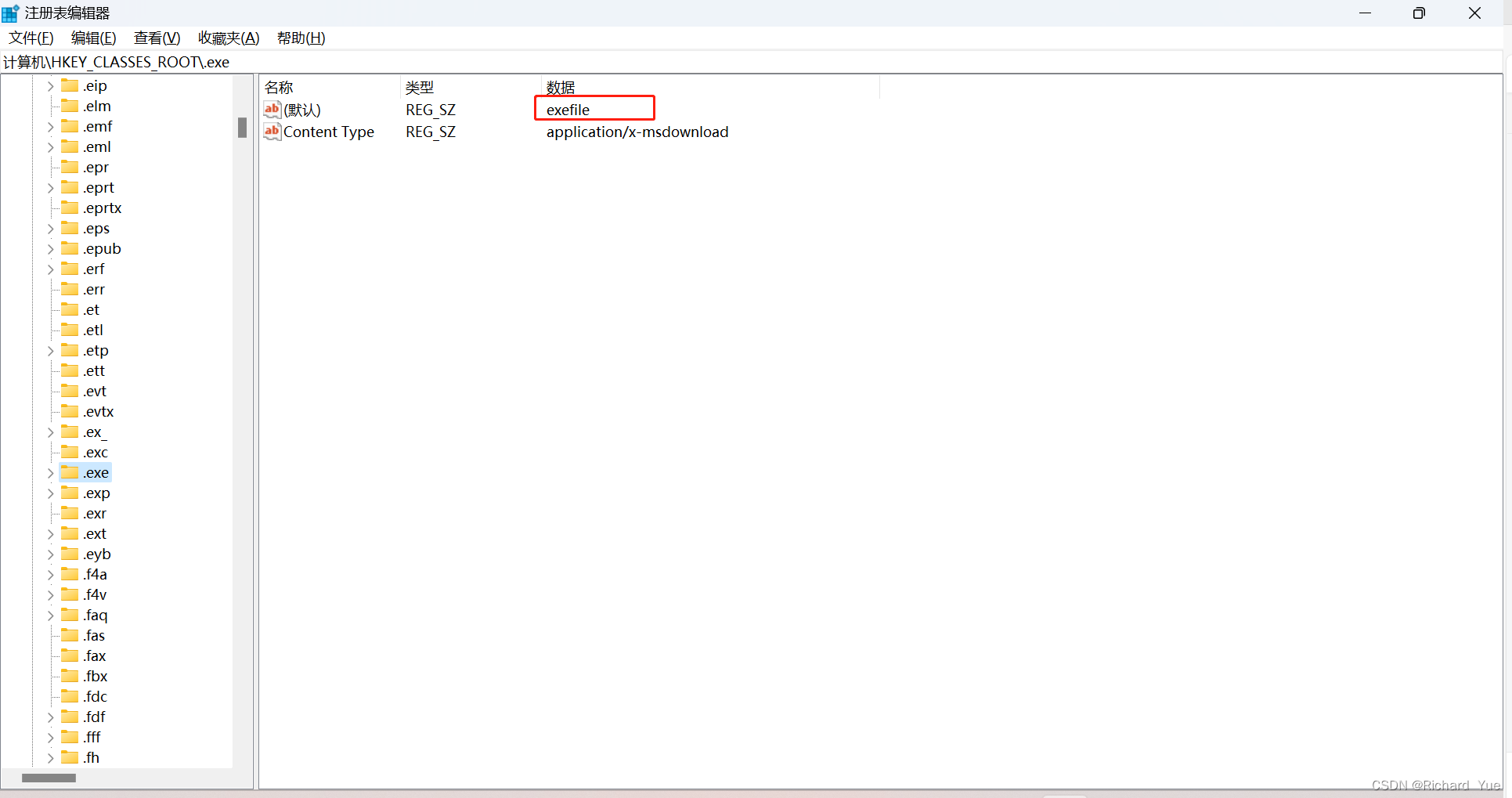
更改注册表exe值后的惨痛经历
装软件时由于执行性文件打不开,搜索教程更改了exefile的值,最后整个电脑崩了,所有EXE都打不开,折腾了5个小时,什么办法都试了,甚至重置电脑都不让,打算拿电脑城修电脑了,突然搜到了一…...

stable diffusion实践操作-LyCORIS
系列文章目录 stable diffusion实践操作 文章目录 系列文章目录前言一、LyCORIS是什么?二、使用步骤1.下载2.安装3 使用 二、整理模型1.LoHa-v1.0-pynoise 总结 前言 LyCORIS,可以理解为lora的加强版本。 LyCORIS - Lora beYond Conventional methods,…...
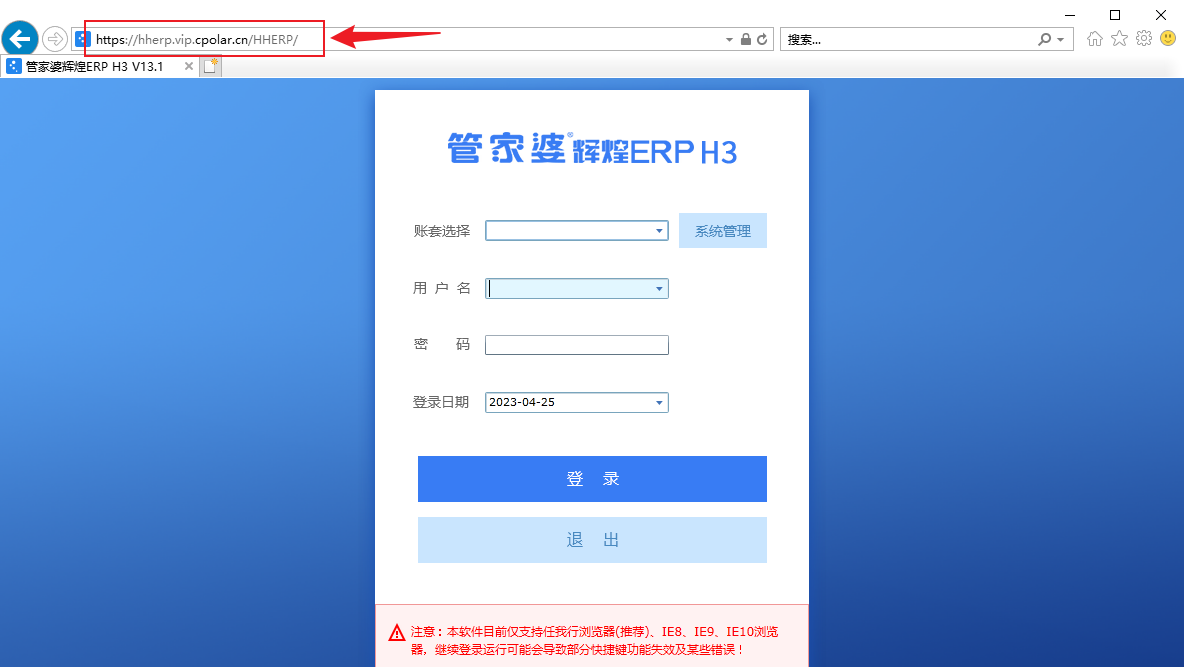
无需公网IP教你如何外网远程访问管家婆ERP进销存
文章目录 前言 1.管家婆服务2. 内网穿透2.1 安装cpolar内网穿透2.2 设置远程访问 3. 固定访问地址4. 配置固定公网访问地址 前言 管家婆辉煌系列产品是中小企业进销存、财务管理一体化的典范软件,历经十余年市场的洗礼,深受广大中小企业的欢迎ÿ…...

Swift使用编解码库Codable
Codable 是 Swift 引入的全新的编解码库,使开发者更方便的解析JSON 或 plist 文件。支持枚举、结构体和类。 Codable协议定义 Codable代表一个同时符合 Decodable 和 Encodable 协议的类型,即可解码且可编码的类型。 typealias Codable Decodable &a…...
Vue + Element UI 前端篇(三):工具模块封装
Vue Element UI 实现权限管理系统 前端篇(三):工具模块封装 封装 axios 模块 封装背景 使用axios发起一个请求是比较简单的事情,但是axios没有进行封装复用,项目越来越大,会引起越来越多的代码冗余&am…...
【pytorch】数据加载dataset和dataloader的使用
1、dataset加载数据集 dataset_tranform torchvision.transforms.Compose([torchvision.transforms.ToTensor(),])train_set torchvision.datasets.CIFAR10(root"./train_dataset",trainTrue,transformdataset_tranform,downloadTrue) test_set torchvision.data…...
搭建单机版FastDFS分布式文件存储系统
一、准备工作 1、下载FastDFS安装包和依赖包 https://codeload.github.com/happyfish100/libfastcommon/tar.gz/V1.0.43 https://codeload.github.com/happyfish100/fastdfs/tar.gz/V6.06 https://codeload.github.com/happyfish100/fastdfs-nginx-module/tar.gz/V1.22 注&…...
【验证码逆向专栏】房某下登录滑块逆向分析
声明 本文章中所有内容仅供学习交流使用,不用于其他任何目的,不提供完整代码,抓包内容、敏感网址、数据接口等均已做脱敏处理,严禁用于商业用途和非法用途,否则由此产生的一切后果均与作者无关! 本文章未…...

Python 3.11 版本是对线程安全做了什么更改吗
问题:这份代码在 3.11.3 中它居然输出 0 ,一度以为自己写错了,抱着不信邪的态度,又搞了个 Python 3.9.7 的环境试了下,果然还是符合自己预期,输出不为 0,想问下 3.11 版本中是做了什么修改吗&am…...
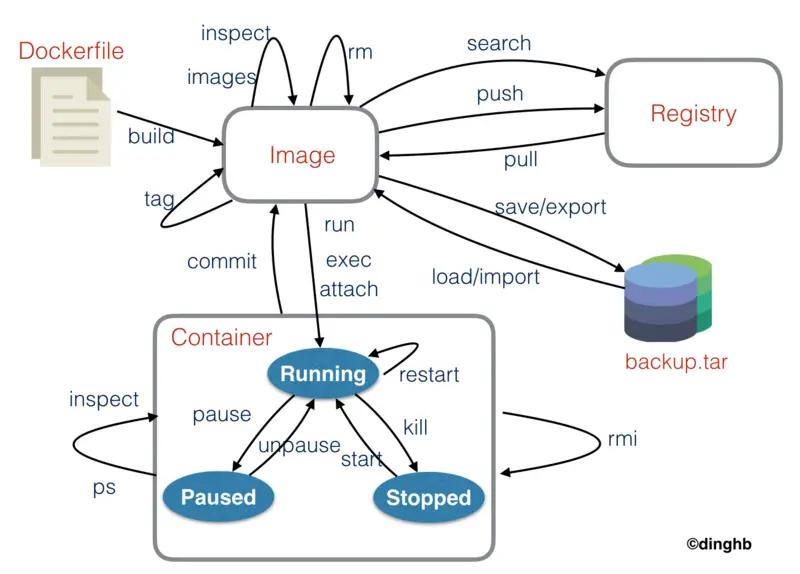
【Docker】镜像的创建、管理与发布
镜像的获取 镜像可以从以下方式获得: 从远程镜像仓库拉取,可以是公有仓库,也可以是私有仓库从Dockerfile构建从文件导入(离线)从容器提交 镜像的基本操作 跟镜像相关的命令如下: $ docker image --help…...
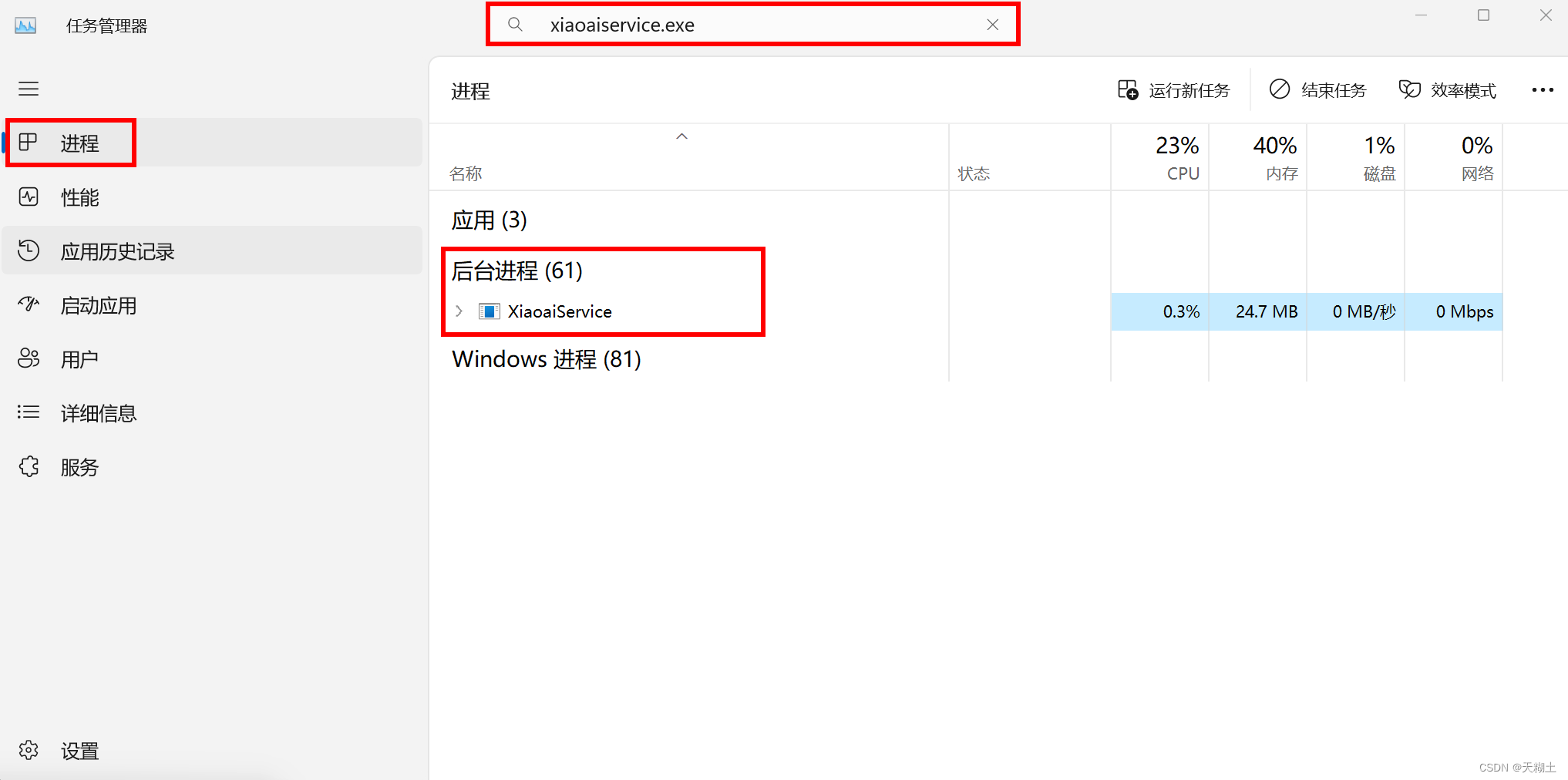
移动硬盘或U盘无法弹出的解决方法
以下内容源于网络资源的学习与整理,如有侵权请告知删除。 最近在红米本win11中总遇到“该设备正在使用中”而无法弹出硬盘的问题。 解法该问题的思路:先定位占用该设备的进程,然后结束该进程。 定位进程 既然设备被占用,那肯定…...
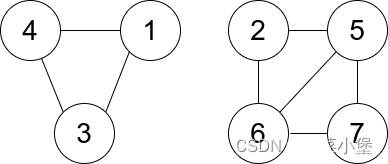
(leetcode1761一个图中连通三元组的最小度数,暴力+剪枝)-------------------Java实现
(leetcode1761一个图中连通三元组的最小度数,暴力剪枝)-------------------Java实现 题目表述 给你一个无向图,整数 n 表示图中节点的数目,edges 数组表示图中的边,其中 edges[i] [ui, vi] ,…...

【漏洞复现】金和OA C6任意文件读取漏洞
漏洞描述 金和OA协同办公管理系统C6软件共有20多个应用模块,160多个应用子模块,涉及的企业管理业务包括协同办公管理、人力资源管理、项目管理、客户关系管理、企业目标管理、费用管理等多个业务范围,从功能型的协同办公平台上升到管理型协同…...
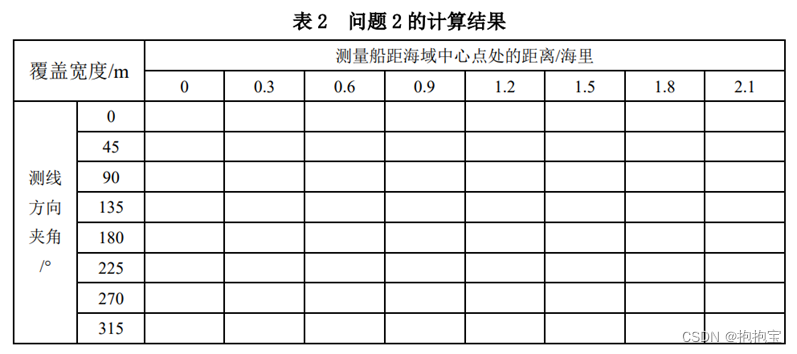
2023年全国大学生数学建模B题
多波束测线问题 1.问题提出 单波束测深是利用声波在水中的传播特性来测量水体深度的技术。声波在均匀介质中作匀 速直线传播,在不同界面上产生反射,利用这一原理,从测量船换能器垂直向海底发射声波信号,并记录从声波发射到信号接…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...
