【leetcode 力扣刷题】数学题之除法:哈希表解决商的循环节➕快速乘求解商
两道和除法相关的力扣题目
- 166. 分数到小数
- 29. 两数相除
- 快速乘
- 解法一:快速乘变种
- 解法二: 二分查找 + 快速乘
166. 分数到小数
题目链接:166. 分数到小数
题目内容:

题目是要我们把一个分数变成一个小数,并以字符串的形式返回。按道理,直接将分子numerator除以分母denominator就得到了小数,转换成string返回就好。题目要求里指出了特殊情况——小数部分如果有循环,就把循环节括在括号里。
那么问题来了,怎么知道有没有循环呢。循环节就是一段循环出现的数字,我们即便是存下来小数部分的每一位数,也不能说有数字重复了就是循环节的开始,比如0.121113,我们不能在1第二次出现的时候就判断上一个1到这个1之前就是循环节。那么是以什么重复出现判断是有循环节呢? A➗B得到商为C,余数为R,计算小数部分时每后移一位将当前余数补0进行运算, 最终余数R==0,表示能够整除,直接将结果转换成string即可;对于有循环节的小数部分,出现重复余数时,表示有循环节。因为从该余数开始计算,一定会再变成这个余数,这样循环下去。那么这个余数第一次计算出的小数,到第二次出现这个余数对应的那位小数,之间的小数就是循环节。 
判断一个余数是否出现过,用hash表记录。由于同时要记录余数,以及余数出现的位置【以便确定循环节开始和结束位置】,因此用map。代码如下(C++):
class Solution {
public:string fractionToDecimal(int numerator, int denominator) {//防止溢出,32位int转换成64位的longlong _numerator = numerator;long _denominator = denominator;//如果分子为0,直接返回零if(_numerator == 0)return "0";//能够整除,直接返回if(_numerator % _denominator == 0) return to_string(_numerator/_denominator);//不能整除的情况,ans表示结果字符串string ans;//异号先添加负号if(_numerator>0&&_denominator<0 || _numerator<0&&_denominator>0){ans.push_back('-');}//都变成绝对值,计算结果数值部分_numerator = abs(_numerator);_denominator = abs(_denominator);//整数部分为0if(_numerator < _denominator)ans.push_back('0');//计算整数部分else{ ans = ans + to_string(_numerator/_denominator);//numerator变成余数_numerator = _numerator % _denominator;}//添加小数点ans.push_back('.'); //map记录余数以及出现的位置unordered_map <long,int> remainder;int idx = ans.size();remainder.insert({_numerator,idx});while(_numerator){_numerator *= 10;ans = ans + to_string(_numerator/_denominator);_numerator = _numerator % _denominator; //如果余数重复出现就break,有循环 if(remainder.count(_numerator))break;remainder.insert({_numerator,++idx}); }//如果余数不为0,就有循环,循环节部分添加()if(_numerator) {ans.insert(remainder[_numerator],"(");ans += ')';}return ans; }
};
29. 两数相除
题目链接:29. 两数相除
题目内容:

理解题意就是做整数除法,返回结果截取小数部分。比如-7/3 = -2,9/4 =2这样。问题在于两个地方:1、给的dividend和divisor,可能结果会溢出;2、不能使用乘法、除法和求余,但是要完成除法求得商。
对于第一个问题,单独考虑一些情况:
- 只有在dividend = -2^31,且divisor = -1的时候,结果为2^31,会溢出;
- 当dividend = 0 时,直接返回0;
- 当divisor = 1 时,直接返回dividend;
对于第二个问题,乘法的本质是加法,可以用快速乘这个方法,用加法来完成乘法操作。除法的本质是减法,而加减是一样的,因此也能用快速乘来完成。 因此本题的重点是快速乘。
另外还需要注意dividend和divisor的符号问题,两个数有四种符号组合,同为正、同为负、一正一负、一负一正,只有在异号的情况下,结果才为负。 确定结果负号后,数值部分计算,就可以将两个数变成都是正的。但此题当dividend 或者 divisor是-2^31时,变成正数就会溢出,因此统一变成负数。
快速乘
快速乘,即用加法来实现乘法,但是不是一个一个加,而是将数字每次翻倍,成倍成倍的加。7*5可以看成是7+7+7+7+7,5的二进制表示是(101),7+7+7+7+7组合一下,等于1*[(7+7)+(7+7)] + 0*(7+7) + 1*7,即第一次是+7,之后是+(7+7),再下一轮是+[(7+7)+(7+7)],每一轮要加的是上一轮的2倍,这个两倍直接用add = add + add来实现,也不需要乘法。每一轮还需要乘以倍数的二进制表达式中对应位的数值【即0或者1】。代码模板如下(C++):
int quick_mul(int x, int n){int ans = 0; int add = x;while(n){if(n&1) //末位为1//【实际上由于n的右移操作,这一步是在看对应位是否为1//比如5 = 101,第一次循环101,末位为1,加上7//第二次10,末位为0,应该加7+7,实际加0//第三次1,末位为1,加上(7+7)+(7+7)】ans += add; //结果ans加上当前的数addadd += add; //add翻倍n >>= 1; //n右移一位}return ans;
}
解法一:快速乘变种
快速乘是在知道了一个数要乘以几之后快速求解答案的过程,除法是要去求被除数是除数的几倍,因此不能直接使用快速乘,但是可以借用快速乘中数字加倍的思想,快速找到商。 判断dividend里面还能不能有一个完整的divisor,是需要|dividend| >= |divisor|,因为都变成了负数,即dividend <= divisor就证明dividend里面有至少一个divisor,商还能加上一部分。那么dividend里面有多少个divisor需要去试,先试有1个【add = divisor】,然后试有2个【add = add + add】,然后试有4个【继续add = add + add】,然后试有8个……这样循环下去,直到某个数使得dividend > add + add了,就说明add + add里面倍数太大了,应该是add里面的倍数。之后dividend减去当前add,剩下的继续去找里面有几个divisor。
这里需要注意判断dividend < add + add,可能有溢出:当add 在-2^31 ~ -2^30之间,add+add小于-2^31,就溢出了,所以应该改成dividend - add < add。
完整代码如下(C++):
class Solution {
public:int divide(int dividend, int divisor) {//特殊情况if(dividend == 0) return 0;if(divisor == 1) return dividend;//可能溢出的情况if(dividend == INT_MIN && divisor == -1) return INT_MAX;if(divisor == INT_MIN){return dividend == INT_MIN ? 1:0;}//防止溢出,正数变复数int rev = 1;if(dividend > 0){dividend = -dividend;rev = -rev;}if(divisor > 0){divisor = -divisor;rev = -rev;}int ans = 0; //被除数和除数都为负数,被除数小于等于除数商才大于0 while(dividend <= divisor){int add = divisor;int result = 1;while(dividend - add <= add){result <<= 1; //当前商翻倍add <<= 1; //翻倍} ans += result; //加上部分结果dividend -= add; //剩余部分继续求商 }return ans*rev; //乘以符号翻转}
};
这里在dividend更新成dividend - add后,add又变成divisor从1倍开始尝试,这其实是多余的,可以将add+=add整翻倍过程的数值记录起来,优化代码(C++):
//记录add翻倍过程中,比dividend小的数值while (add.back() >= dividend - add.back()) {add.push_back(add.back() + add.back());
}
int ans = 0;
for (int i = add.size() - 1; i >= 0; --i) {//dividend比add[i]更小,add里面的倍数能够加载商里面if (add[i] >= dividend) {//下标是i,对应的倍数是2^i,可以用左移i位来实现ans += (1 << i);//dividend减去对应的adddividend -= add[i];}
}
解法二: 二分查找 + 快速乘
还有一种办法是尝试每一个n,看当前的n*divisor和dividend的关系,因为dividend和divisor都变成了负数,因此dividend < n*divisor才能满足条件,n继续增大去比较。这里的n*divisor就用上述的快速乘去实现——需要改动一点,就是最后返回dividend 和 n*divisor 大小关系。
n是0到2^31-1之间的一个数,要找到合适的n,可以用二分法,相较于依次挨个比较,时间复杂度更优,代码如下(C++):
class Solution {
public:bool quick_mul(int divisor, int n, int dividend){int ans = 0;int add = divisor;while(n){//末位为1,要加上一部分if(n&1){//如果计算过程中发现ans更小,就说明n太大了,直接返回falseif(dividend - add > ans ) return false;ans += add;}//如果当前不是最后一位,还要循环几轮if(n!=1){//而下一轮要用到的add已经比dividend更小【里面包括的divisor的倍数更多】//直接终止,返回falseif(dividend - add > add)return false;add += add;}n >>= 1;}return true;}int divide(int dividend, int divisor) {//特殊情况if(dividend == 0) return 0;if(divisor == 1) return dividend;//可能溢出的情况if(dividend == INT_MIN && divisor == -1) return INT_MAX;if(divisor == INT_MIN){return dividend == INT_MIN ? 1:0;}//防止溢出,正数变复数int rev = 1;if(dividend > 0){dividend = -dividend;rev = -rev;}if(divisor > 0){divisor = -divisor;rev = -rev;}int ans = 0, left = 1, right = INT_MAX;//二分查找的过程while(left <= right){int mid = left + ((right - left)>>1);if (quick_mul(divisor, mid, dividend)){ans = mid; //当前的mid是dividend <= mid * dividor,先赋值给andif(mid == INT_MAX)break;left = mid + 1;}else{right = mid - 1;}} return ans*rev; //乘以符号翻转}
};
二分查找过程是官方题解,但是我不太理解为什么一定要and = mid这一步赋值,直接返回mid是不对的……
解释:在-7/3这个情况下,结果是-2;left一直为1,right一直减小到3,此时mid = 2,对应quick_mul返回true,left = 3;此时仍然满足循环条件,mid 更新为 3 ,但是此时quick_mul返回的是false。也就是一个quick_mul返回true的mid可能是答案,需要记录,之后如果还有mid满足条件就更新。但是满足条件后mid可能还会更新,但更新后可能就不满足条件了。因此直接返回mul是不正确的。
相关文章:

【leetcode 力扣刷题】数学题之除法:哈希表解决商的循环节➕快速乘求解商
两道和除法相关的力扣题目 166. 分数到小数29. 两数相除快速乘解法一:快速乘变种解法二: 二分查找 快速乘 166. 分数到小数 题目链接:166. 分数到小数 题目内容: 题目是要我们把一个分数变成一个小数,并以字符串的形…...
方法-set.union())
Union类型和集合的union()方法-set.union()
Union类型和集合的Union 方法 一、Union类型1.Union类型由来2.Union类型的语法3.Union类型的使用4.一些等价写法 二、Set.union()union() 语法示例代码 一、Union类型 1.Union类型由来 Python中的Union类型是 3.10版本引入的新功能之一。它是一种特殊的类型注释,用…...
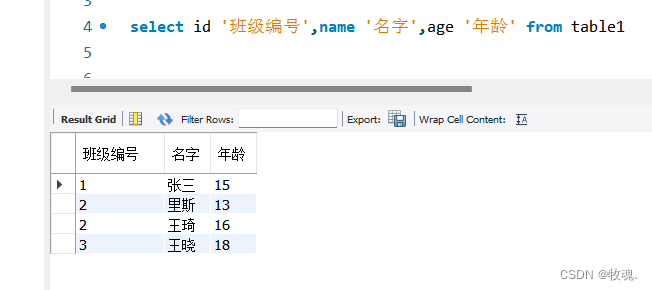
简明SQL别名指南:掌握AS实现列名更名
在 SQL 查询中,使用 {原始字段名} as {别名} 的语法来为查询结果的列赋予更直观的名称,以提高查询结果的可读性和可理解性。 以下是用到的表。 用AS更名 例如,查询表1的name字段,并将其更名为"名字",同时查…...

基于量子密钥分发和区块链技术的新一代加密通信系统
量子通信与区块链构建下一代加密通信基础设施 量子技术和区块链技术是国家信息安全和国家数字化转型的重要组成部分,在国家战略中具有重要地位。“十四五”规划纲要将“加快数字发展建设数字中国”作为独立篇章,指出要进一步明确发展云计算、大数据、物联…...

网络安全-子域名收集
本文为作者学习文章,按作者习惯写成,如有错误或需要追加内容请留言(不喜勿喷) 本文为追加文章,后期慢慢追加 子域名 子域名指二级域名,二级域名是顶级域名(一级域名)的下一级比如mail.heetian.com和bbs.heetian.com…...

go-zero jwt 鉴权快速实战
前面我们分享了 go-zero 的快速实战以及日志组件的剖析,本次我们来实战使用 go-zero jwt 鉴权 本次文章主要是分享关于 go-zero 中 jwt 的使用方式,会以一个 demo 的方式来进行实战,对于使用 goctl 工具以及安装细节就不在赘述,有…...

9.8day58 单调栈
739. 每日温度 - 力扣(LeetCode) 知识点:1.建栈 2.如果后面要加入的数小于栈顶元素就把数组的下标压进栈里 3.反之 就让该数于栈顶元素进行比较 如果该数大于栈顶元素(while) 就把栈顶元素下表对应的arr数组的值进行…...
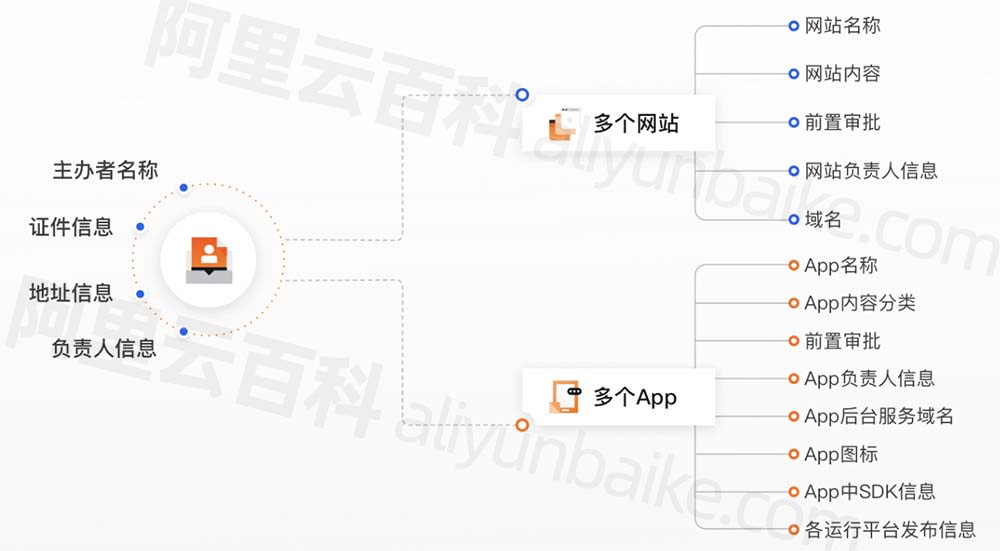
快速完成工信部APP备案流程_以阿里云APP备案为例
阿里云APP备案流程分为6步,APP备案成功后应用可以上架,登录阿里云账号填写APP信息,等待阿里云初审,初审通过后进行工信部短信核验,管局审核通过后APP即可备案成功,最后移动APP应用可以分发平台上架…...
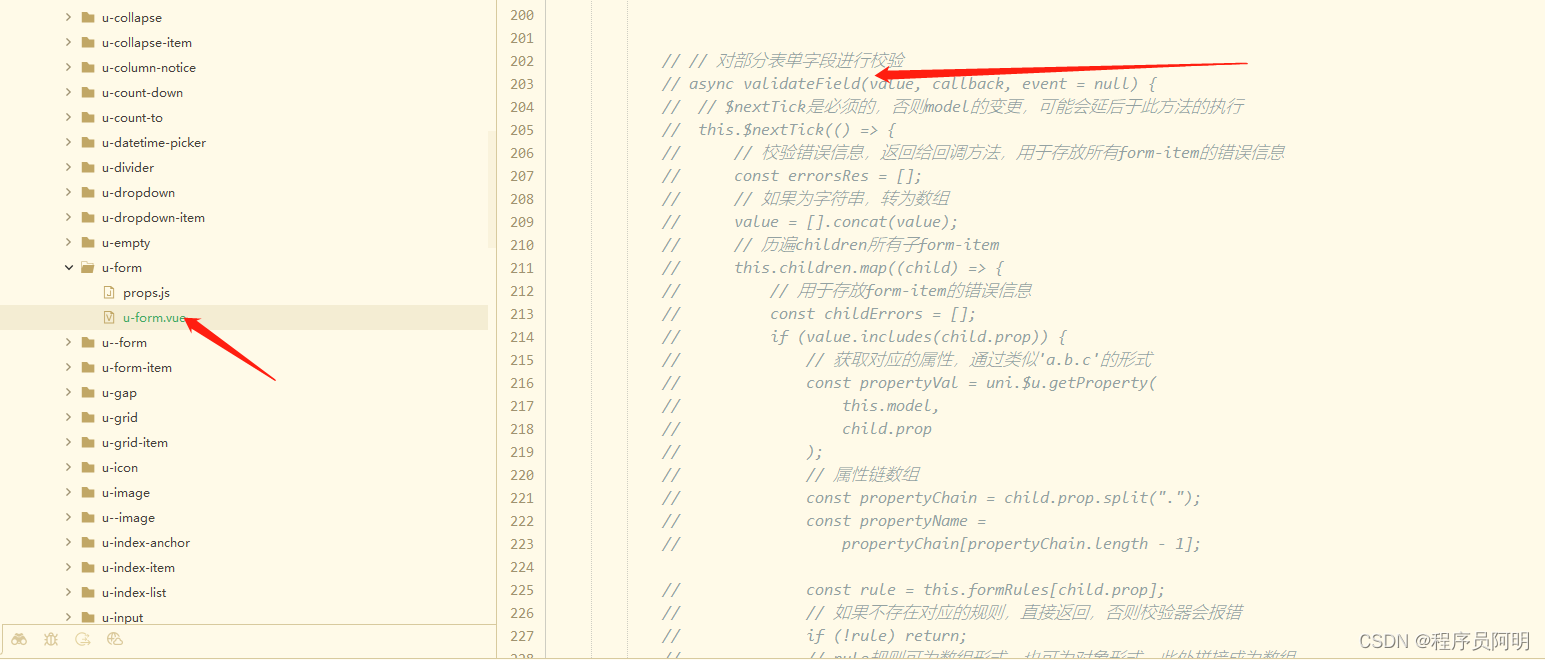
uniapp中UView中 u-form表单在v-for循环下如何进行表单校验
1、数据data格式 注:rule绑定的tableFromRule中要和表单tableFrom下面放置一个同名数组,确保u-form能找到 tableFrom: {tableData: [//数据详情列表]},tableFromRule: {//校验tableData: [//数据详情列表]},formRules:{localation:[{required: true,mes…...

工作新时代,腾讯轻联塑造高效办公未来
腾讯轻联:开启便捷、高效的集成新纪元 ⭐ 写在前面⭐ 使用模板快速起步⭐ 自定义流程初体验⭐ 无与伦比的集成强者⭐ 写在最后 ⭐ 写在前面 在当今竞争激烈的商业环境中,提高企业的办公效率和工作流程自动化变得至关重要。腾讯轻联,作为新一…...

JavaScript实现广告倒计时和跳过广告
倒计时和跳过广告 最近打开手机上的app,映入眼帘的都是一个几秒的广告,带有倒计时,当然如果不喜欢的话可以点击跳过,跳过广告其实质应该就是关闭广告。以前用JavaScript做过一个定时关闭的广告,于是把代码完善了一下&…...
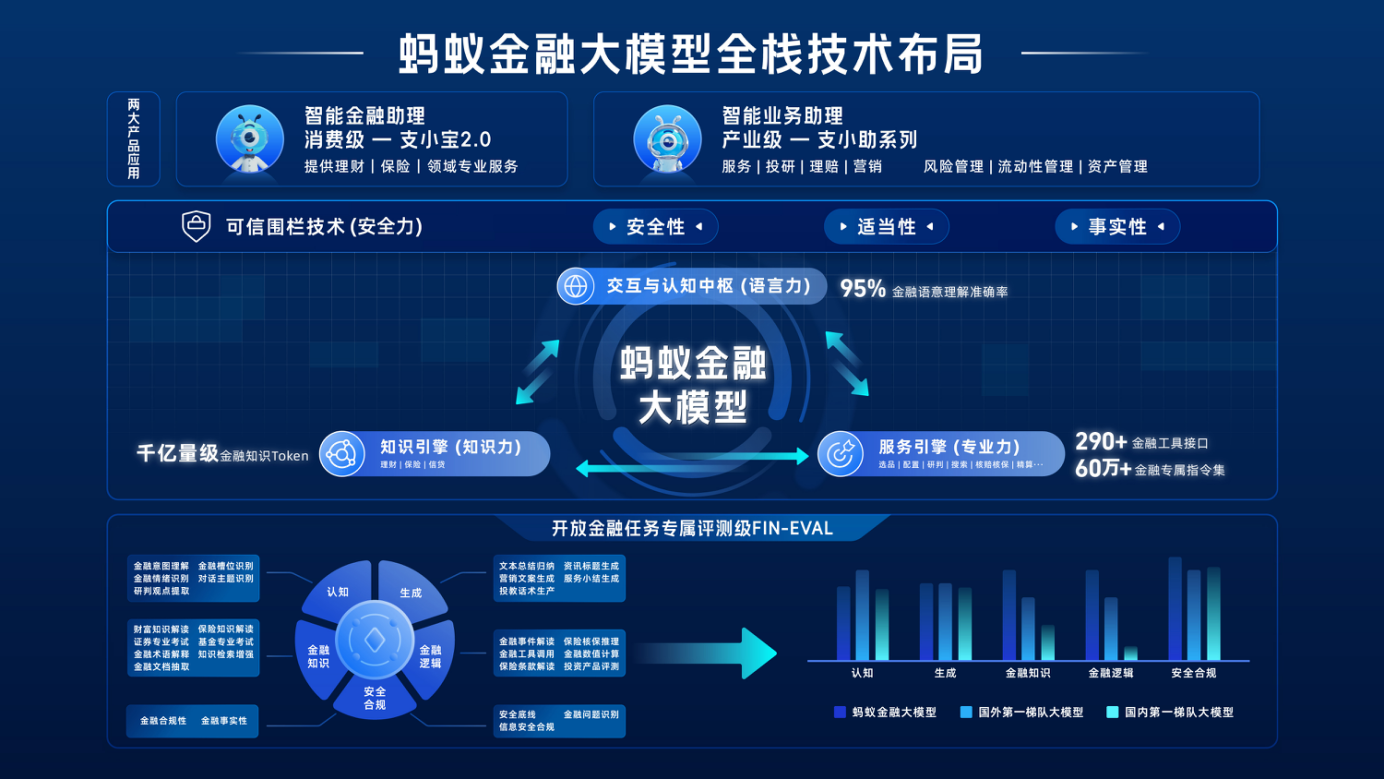
蚂蚁发布金融大模型:两大应用产品支小宝2.0、支小助将在完成备案后
9月8日,在上海举办的外滩大会上,蚂蚁集团正式发布金融大模型。据了解,蚂蚁金融大 模型基于蚂蚁自研基础大模型,针对金融产业深度定制,底层算力集群达到万卡规模。该大 模型聚焦真实的金融场景需求,在“认知…...

Jenkins 持续集成:Linux 系统 两台机器互相免密登录
背景知识 我们把public key放在远程系统合适的位置,然后从本地开始进行ssh连接。 此时,远程的sshd会产生一个随机数并用我们产生的public key进行加密后发给本地,本地会用private key进行解密并把这个随机数发回给远程系统。 最后…...

Golang-GJSON 快速而简单的方法来从 json 文档获取值
GJSON 是一个 Go 包,它提供了一种快速而简单的方法来从 json 文档获取值。它具有单行搜索、点符号路径、迭代和解析 json 行等功能。 GJSON 也可用于Python和Rust 入门 安装中 要开始使用GJSON 请安装 Go 并运行 go get : $ go get -u github.com/ti…...

echarts根据x轴数据长度判断是否倾斜展示/柱状图上方显示数字
showChart1() { // 通过id初始化let chart1 echarts.init(document.getElementById(this.idName))var option {// 到容器的距离grid: {top: 18,left: 0,right: 4,bottom: 0,},xAxis: [{type: category,data: this.xData,axisLine: {lineStyle: {color: rgba(255, 255, 255, .…...

Eviews用向量自回归模型VAR实证分析公路交通通车里程与经济发展GDP协整关系时间序列数据和脉冲响应可视化...
全文下载链接:http://tecdat.cn/?p27784 河源市是国务院1988年1月7日批准设立的地级市,为了深入研究河源市公路交通与经济发展的关系,本文选取了1988-2014年河源市建市以来24年的地区生产总值(GDP)和公路通…...
群晖NAS:通过Docker 部署宝塔面板【注册表:cyberbolt/baota】
群晖NAS:通过 Docker 部署宝塔面板【注册表:pch18/baota】 由于 docker 源地址被墙,在面板里面查询不到注册表,使用 ssh 命令行拉取 1、打开 SSH,链接后打开命令行 这里不赘述,具体自行百度 2、下载 镜像…...
pdfjs在线预览组件的使用
前言 pdfjs在线预览组件。 原生浏览器预览pdf文件,存在pdf xss跨站攻击风险。推荐使用pdfjs第三方组件在线预览pdf文件。 如何使用 下载 官方插件下载地址:https://mozilla.github.io/pdf.js/getting_started/ 安装 把下载的文件复制到项目中 使用pd…...

python线程、协程
线程 创建线程对象 from threading import Threadt Thread() # 功能:创建线程对象 # 参数:target 绑定线程函数 # args 元组 给线程函数位置传参 # kwargs 字典 给线程函数键值传参启动线程 t.start() # 启动线程回收线程 t.join([timeout]) # …...

AttributeError: module ‘OpenSSL.SSL’ has no attribute ‘SSLv3_METHOD
这个错误是由于在OpenSSL.SSL模块中找不到SSLv3_METHOD属性导致的。解决这个问题的方法如下: 首先,确保你已经安装了最新版本的cryptography和pyOpenSSL。你可以使用以下命令卸载并重新安装它们: 卸载cryptography:pip uninstall …...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...
