day-41 代码随想录算法训练营(19)动态规划 part 03
343.整数拆分
思路:
- 1.dp存储的是第i个数,拆分之后最大乘积
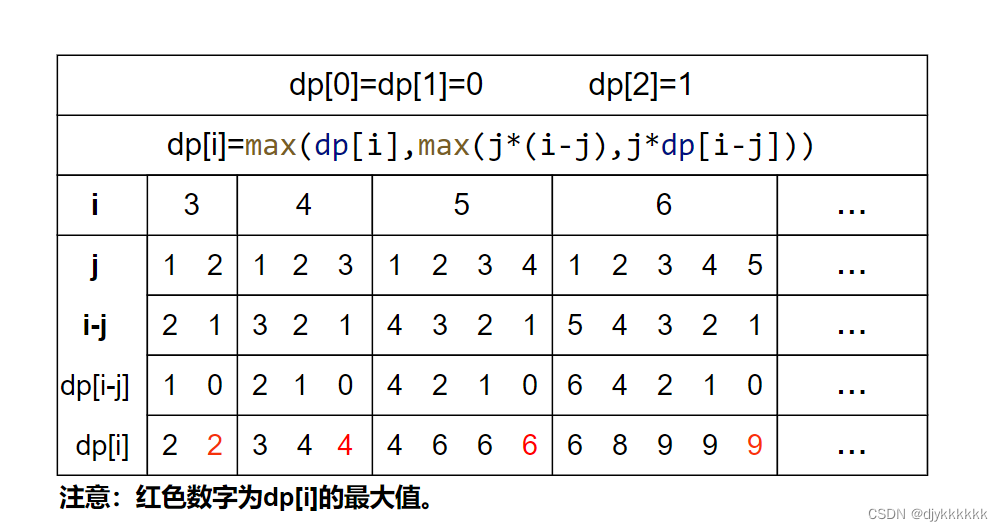
- 2.dp[i]=max(dp[i],max(j*(i-j),j*dp[i-j]));
- 3.初始化:dp[0]=dp[1]=0,dp[2]=1;
- 4.遍历顺序:外层循环 3-n,内层循环 1-i
2.涉及两次取max:
- dp[i] 表示拆开的最大乘积,因为涉及多次计算
- j*(i-j) 表示拆成两个数
- j*dp[i-j] 表示拆成两个以上的数(dp[i-j] 就是剩下没拆的数,拆开的最大乘积)
class Solution {
public:int integerBreak(int n) {vector<int>dp(n+1,0);dp[2]=1;for(int i=3;i<=n;i++){for(int j=1;j<i;j++){dp[i]=max(dp[i],max(j*(i-j),j*dp[i-j]));cout<<i<<" "<<dp[i]<<endl;}}return dp[n];}
};
96.不同的二叉搜索树
分析:1-n有几种二叉搜索树
-
1.以1-n每个数为根节点
-
2.判断根节点左边和右边各有几个节点,只有结点数相同,组合的二叉搜索树种数就是一样的。
思路:
- 1.dp存储n个节点有多少种二叉搜索树
- 2.dp[i]=dp[i-1]*dp[n-i];
- 3.初始化:dp[0]=dp[1]=1,dp[2]=2;
- 4.遍历顺序:3-n
416.分割等和子集
分析:
- 数组要求分成两个等和子集,所以一定要有子集和为总和的一半
- 转换为:在集合中找数字,看能否组合成总和的一半值的子集
- 转换为:在总和一半容量的背包里,寻找子集刚好装满
思路一:
1.dp存储:容量为 j 时,装入物品的最大值
2.dp [ j ] =max ( dp [ j ] ,dp [ j - nums [i] ] + nums [ i ] )
3.初始化:所有值初始化为0
4.遍历顺序:外层遍历数字(顺序,物品),内层遍历数字(倒序,背包容量)
class Solution {
public:bool canPartition(vector<int>& nums) {int total=0;for(auto it:nums) total+=it;//求出总和if(total%2!=0) return false;//过滤不可拆成两半的情况int target=total/2;//背包容量vector<int>dp(10001,0);for(int i=0;i<nums.size();i++){//遍历物品for(int j=target;j>=nums[i];j--){//背包容量递减,最少能装入一个物品dp[j]=max(dp[j],dp[j-nums[i]]+nums[i]);//dp[j] 是不装当前物品//dp[j-nums[i]]+nums[i] 是装当前物品}}if(dp[target]==target) return true;//背包容量为target,装了target重的物品return false;}
};相关文章:

day-41 代码随想录算法训练营(19)动态规划 part 03
343.整数拆分 思路: 1.dp存储的是第i个数,拆分之后最大乘积2.dp[i]max(dp[i],max(j*(i-j),j*dp[i-j]));3.初始化:dp[0]dp[1]0,dp[2]1;4.遍历顺序:外层循环 3-n,内层循环 1-i 2.涉及两次取max: dp[i] 表…...
)
K8S安装部署 初始化操作(一)
准备好服务器和服务器资源 ip hostnameip资源 (2核2G也可以)k8s-master 192.168.37.1184核 4G 40G硬盘k8s-node1192.168.37.1192核 2G 20G硬盘k8s-node2192.168.37.1202核 2G 20G硬盘 初始操作三台同时执行 1、关闭防火墙 [rootlocalhost ~]# s…...
【多线程案例】单例模式(懒汉模式和饿汉模式)
文章目录 1. 什么是单例模式?2. 立即加载/“饿汉模式”3. 延时加载/“懒汉模式”3.1 第一版3.2 第二版3.3 第三版3.4 第四版 1. 什么是单例模式? 提起单例模式,就必须介绍设计模式,而设计模式就是在软件设计中,针对特殊…...
Anaconda - 操作系统安装程序 简要介绍
Anaconda 简要介绍 1. Anaconda 简介2. Anaconda 体系结构3. Anaconda 开发模型4. Anaconda 启动概述5. Anaconda 源码1. 接口2. 自定义组件3. 硬盘分区:使用python-blivet包4. Bootloader5. 各个步骤的配置:6. 安装软件包:7. 安装控制&#…...

【数据库设计】向量搜索HNSW算法优化
做向量存储的过程中,遇到向量搜索的情况处理,HNSW算法是目前向量搜索的主要算法之一,采用的是图算法,主要的问题是使用内存大,训练时间长。做算法优化过程中获得部分技巧,分享出来。 一、算法本身的优化 对…...

多通道振弦数据记录仪应用桥梁安全监测的关键要点
多通道振弦数据记录仪应用桥梁安全监测的关键要点 随着近年来桥梁建设和维护的不断推进,桥梁安全监测越来越成为公共关注的焦点。多通道振弦数据记录仪因其高效、准确的数据采集和处理能力,已经成为桥梁安全监测中不可或缺的设备。本文将从以下几个方面…...

深入了解HTTP代理的工作原理
HTTP代理是一种常见的网络代理方式,它可以帮助用户隐藏自己的IP地址,保护个人隐私和安全。了解HTTP代理的工作原理对于使用HTTP代理的用户来说非常重要。本文将深入介绍HTTP代理的工作原理。 代理服务器的作用 HTTP代理的工作原理基于代理服务器的作用。…...

2023年高教社杯数学建模国赛选题人数+C题进阶版修改思路详解
C题思路 修改版 C题保奖 数据预处理 3σ原则 区间判断法、人为判定 问题 1 聚类分析进行简单的分类 相互关系 数据服从正态分布(K-S检验等判定分布类型后) 才能做person相关性 图表结合(热力图、数据结果表) 分布规律 宏…...
第三章微服务配置中心
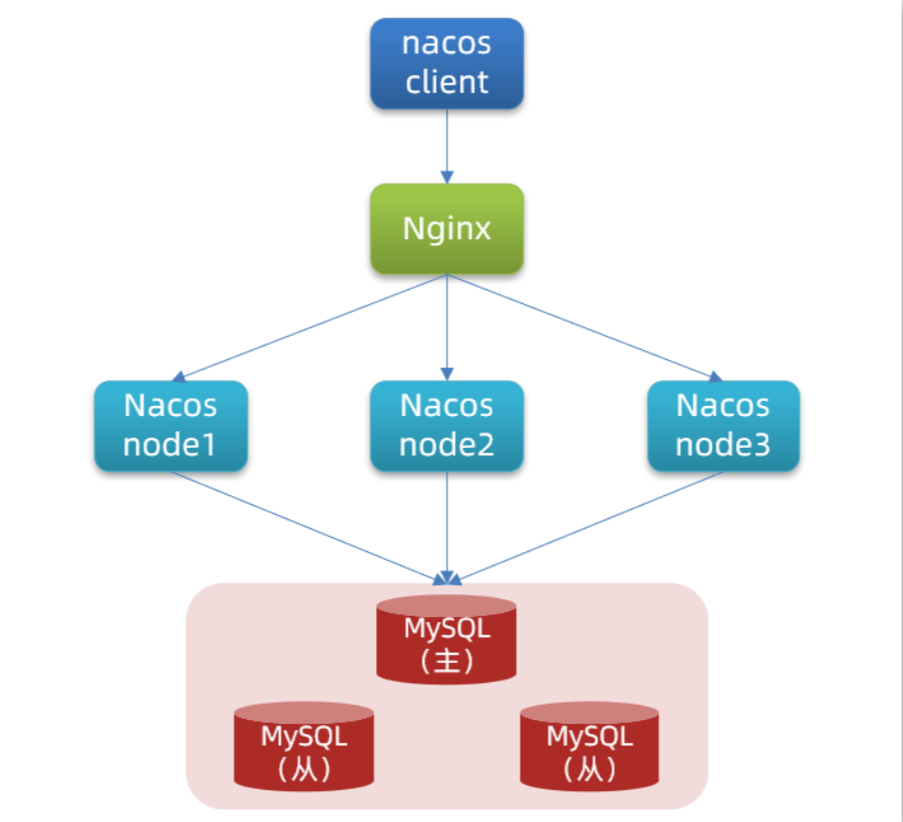
文章目录 Nacos配置中心统一配置管理在nacos中添加配置文件从微服务拉取配置 配置热更新多环境共享配置 搭建Nacos集群搭建集群初始化数据库配置Nacos启动nginx反向代理 Nacos配置中心 Nacos配置管理 Nacos除了可以做注册中心,同样可以做配置管理来使用。 统一配置…...

箭头函数(arrow function)与普通函数之间的区别是什么?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 语法简洁性:⭐ this 的绑定:⭐ 不能用作构造函数:⭐ 没有 arguments 对象:⭐ 不适用于方法:⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上…...
JMeter 4.0 如何获取cookie
文章目录 前言JMeter 4.0 如何获取cookie1. 修改jmeter.properties 文件2. 添加HTTP Cookie 管理器3. 获取cookie信息 前言 如果您觉得有用的话,记得给博主点个赞,评论,收藏一键三连啊,写作不易啊^ _ ^。 而且听说点赞的人每天…...
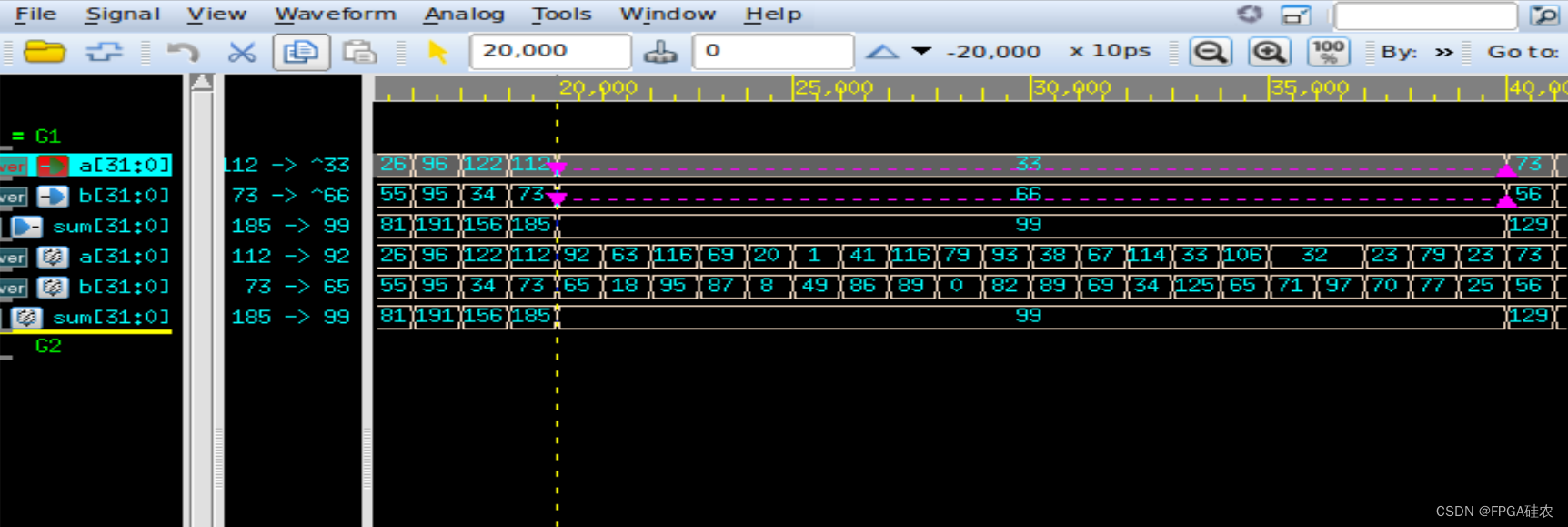
【数字IC/FPGA】Verilog中的force和release
在Verilog中,将force用于variable会覆盖掉过程赋值,或者assign引导的连续(procedural assign)赋值,直到release。 下面通过一个简单的例子展示其用法: 加法器代码 module adder ( input logic [31:0] a, …...

进阶C语言-指针的进阶(上)
指针的进阶 📖1.字符指针📖2.指针数组📖3.数组指针🎈3.1 数组指针的定义🎈3.2 &数组名VS数组名🎈3.3 数组指针的使用 📖4.数组参数、指针参数🎈4.1一维数组传参🎈4.2…...

初始化一个 vite + vue 项目
创建项目 首先使用以下命令创建一个vite项目 npm create vite然后根据提示命令 cd 到刚创建的项目目录下,使用npm install安装所需要的依赖包,再使用npm run dev即可启动项目 配置 vite.config.js 添加process.env配置,如果下面 vue-route…...

关于B+树
在数据库管理系统中,使用b树作为索引的数据结构,相比于B树和二叉树,有以下几个好处: b树的非叶子节点只存储关键字和指针,不存储数据,这样可以增加每个节点的关键字数量,降低树的高度ÿ…...

axios 请求和响应拦截器
1. 创建实例 使用 axios.create() 使用自定义配置创建一个 axios 实例。 const $http axios.create({timeout: 1000,headers: {Content-Type: application/json,} })2. 拦截器 在请求或响应被 then 或者 catch 处理前拦截他们,拦截分为请求拦截和响应拦截。 //…...

Element-ui select远程搜索
template部分: <el-form-item label"用户" prop"userId"><el-selectv-model"temp.userId"placeholder"用户"filterableremote:reserve-keyword"false":remote-method"remoteMethod":loading"loadi…...

【Express.js】Docker部署
Docker部署 本节我们来介绍如何使用 Docker 部署 express 应用 准备工作 linux 系统安装好 Docker一个基础的 evp-express-cli 项目,选上 pkg 工具包Docker 的详细用法本文不做介绍,请先自行查阅了解 在 Docker 中部署源码 一个很简单的部署方法就是…...

面试2:通用能力
15丨如何做好开场:给自我介绍加“特效 第一层,满足面试官对信息的期待 这是对自我介绍的基本要求,把个人信息、主要经历、经验和技能有条理地组织起来, 有逻辑地讲出来。需要找出多段经历的关联性和发展变化,形成连…...
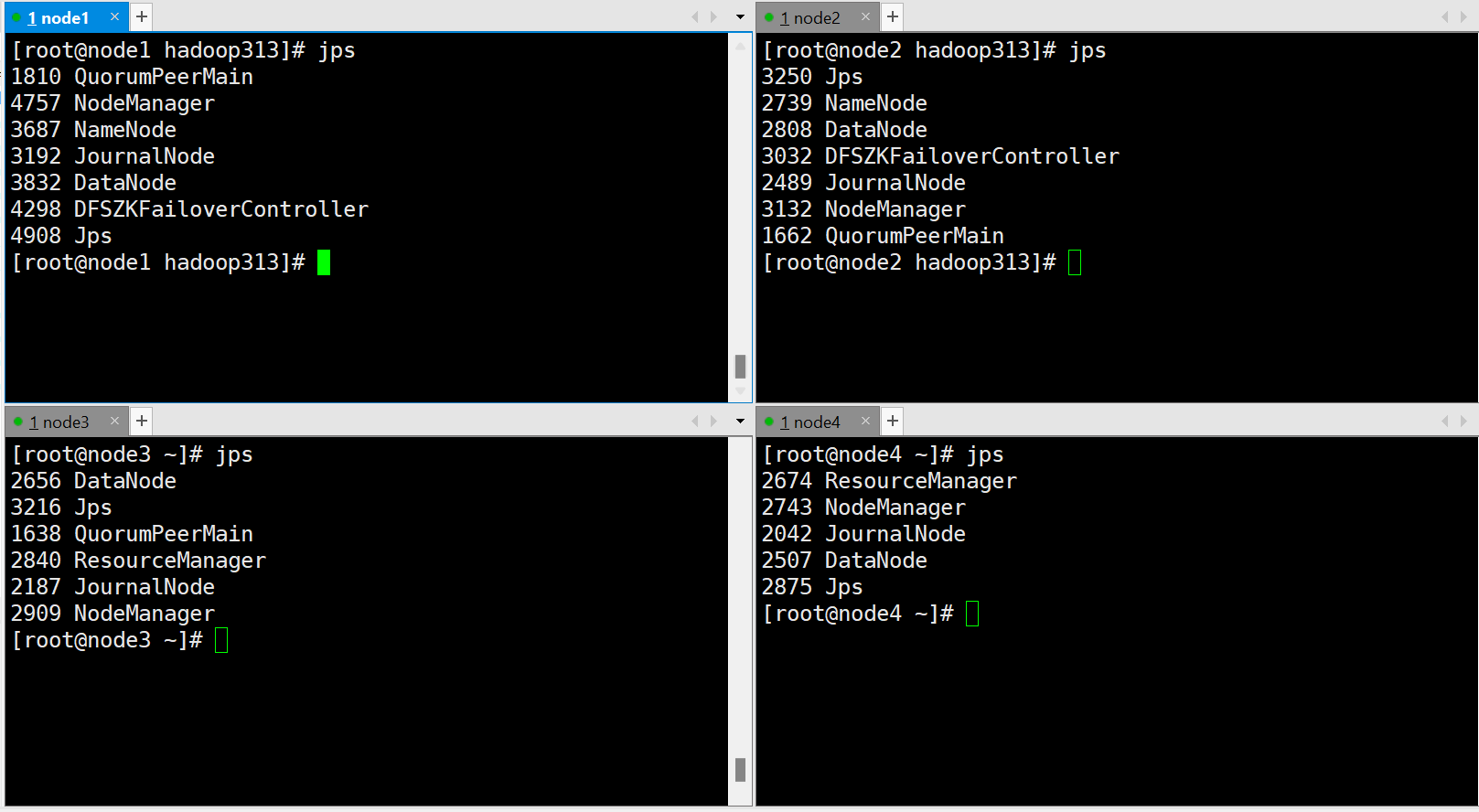
zookeeper/HA集群配置
1.zookeep配置 1.1 安装4台虚拟机 (1)按照如下设置准备四台虚拟机,其中三台作为zookeeper,配置每台机器相应的IP,hostname,下载vim,ntpdate配置定时器定时更新时间,psmiscÿ…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
