MySQL——子查询
2023.9.8
相关学习笔记:
#子查询
/*
含义:
出现在其他语句中的select语句,称为子查询或内查询
外部的查询语句,称为主查询或外查询分类:
按子查询出现的位置:select后面:仅仅支持标量子查询from后面:支持表子查询where或having后面:★标量子查询(单行) √列子查询 (多行) √行子查询exists后面(相关子查询)表子查询
按结果集的行列数不同:标量子查询(结果集只有一行一列)列子查询(结果集只有一列多行)行子查询(结果集有一行多列)表子查询(结果集一般为多行多列)*/#一、where或having后面
/*
1、标量子查询(单行子查询)
2、列子查询(多行子查询)3、行子查询(多列多行)特点:
①子查询放在小括号内
②子查询一般放在条件的右侧
③标量子查询,一般搭配着单行操作符使用
> < >= <= = <>列子查询,一般搭配着多行操作符使用
in、any/some、all④子查询的执行优先于主查询执行,主查询的条件用到了子查询的结果*/
#1.标量子查询(重点)
#案例1:谁的工资比 Abel 高?
SELECT `last_name`
FROM `employees`
WHERE salary>(SELECT salary FROM `employees` WHERE `last_name`='Abel');
#案例2:返回job_id与141号员工相同,salary比143号员工多的员工 姓名,job_id 和工资
SELECT `last_name`,`job_id`,`salary`
FROM `employees`
WHERE `job_id` = (SELECT `job_id` FROM `employees` WHERE `employee_id`=141)
AND salary > (SELECT salary FROM `employees` WHERE `employee_id`=143);
#案例3:返回公司工资最少的员工的last_name,job_id和salary
SELECT `last_name`,`job_id`,`salary`
FROM `employees`
WHERE salary=(SELECT MIN(salary) FROM `employees`);
#案例4:查询最低工资大于50号部门最低工资的部门id和其最低工资
SELECT `department_id`,MIN(salary)
FROM `employees`
GROUP BY `department_id`
HAVING MIN(salary)>(SELECT MIN(salary) FROM `employees` WHERE `department_id`=50);#2.列子查询(多行子查询)
#案例1:返回location_id是1400或1700的部门中的所有员工姓名
SELECT `last_name`
FROM `employees`
WHERE `department_id` IN
(SELECT `department_id`
FROM `departments`
WHERE `location_id` IN (1400,1700));
#案例2:返回其它工种中比job_id为‘IT_PROG’工种任一工资低的员工的员工号、姓名、job_id 以及salary
SELECT `employee_id`,`last_name`,`job_id`,`salary`
FROM `employees`
WHERE salary < ANY
(SELECT salary
FROM `employees`
WHERE `job_id` = 'IT_PROG')
AND `job_id` != 'IT_PROG';
#案例3:返回其它部门中比job_id为‘IT_PROG’部门所有工资都低的员工的员工号、姓名、job_id 以及salary
SELECT last_name,employee_id,job_id,salary
FROM employees
WHERE salary<ALL(SELECT DISTINCT salaryFROM employeesWHERE job_id = 'IT_PROG') AND job_id<>'IT_PROG';#3、行子查询(结果集一行多列或多行多列)
#案例:查询员工编号最小并且工资最高的员工信息
SELECT *
FROM `employees`
WHERE (`employee_id`,`salary`) =
(SELECT MIN(`employee_id`),MAX(salary) FROM `employees`);#二、select后面
/*
仅仅支持标量子查询
*/#案例:查询每个部门的员工个数
SELECT d.`department_name`,(
SELECT COUNT(*) FROM `employees` e WHERE e.`department_id` = d.`department_id`
) 员工人数
FROM `departments` d;
#案例2:查询员工号=102的部门名
SELECT `department_name`
FROM `departments` d
INNER JOIN `employees` e
ON d.`department_id` = e.`department_id`
WHERE `employee_id` = 102;#三、from后面
/*
将子查询结果充当一张表,要求必须起别名
*/#案例:查询每个部门的平均工资的工资等级
SELECT Ag_dep.*,j.`grade_level`
FROM(SELECT `department_id`,AVG(salary) agFROM `employees`GROUP BY `department_id`
) Ag_dep
INNER JOIN `job_grades` j
ON Ag_dep.ag BETWEEN `lowest_sal` AND `highest_sal`;#四、exists后面(相关子查询)/*
语法:
exists(完整的查询语句)
结果:
1或0
*/SELECT EXISTS(SELECT employee_id FROM employees WHERE salary=300000);#案例1:查询有员工的部门名
#用exists实现
SELECT `department_name`
FROM `departments` d
WHERE EXISTS(
SELECT *
FROM `employees` e
WHERE d.`department_id`=e.`department_id`
);
#用in来实现
SELECT `department_name`
FROM `departments` d
WHERE d.`department_id` IN (
SELECT `department_id`
FROM `employees`);
#案例2:查询没有女朋友的男神信息
#in实现
SELECT bo.*
FROM `boys` bo
WHERE bo.`id` NOT IN (
SELECT `boyfriend_id`
FROM `beauty`);
#exists实现
SELECT bo.*
FROM `boys` bo
WHERE NOT EXISTS(
SELECT `boyfriend_id`
FROM `beauty` b
WHERE bo.`id`=b.`boyfriend_id`);课后习题:
#课后习题
#1.查询和Zlotkey相同部门的员工姓名和工资
SELECT `last_name`,salary
FROM `employees`
WHERE `department_id` = (
SELECT `department_id`
FROM `employees`
WHERE `last_name`='Zlotkey');
#2.查询工资比公司平均工资高的员工的员工号,姓名和工资。
SELECT `employee_id`,`last_name`,salary
FROM `employees`
WHERE salary>(
SELECT AVG(salary)
FROM `employees`);
#3.查询各部门中工资比本部门平均工资高的员工的员工号, 姓名和工资
SELECT `employee_id`,`last_name`,`salary`
FROM `employees` e
INNER JOIN (SELECT `department_id`,AVG(salary) agFROM `employees`GROUP BY `department_id`
) b
ON e.`department_id`=b.`department_id`
WHERE salary > b.ag;
#4.查询和姓名中包含字母u的员工在相同部门的员工的员工号和姓名
SELECT `employee_id`,`last_name`
FROM `employees`
WHERE `department_id` IN(
SELECT `department_id`
FROM `employees`
WHERE `last_name` LIKE '%u%'
);
#5. 查询在部门的location_id为1700的部门工作的员工的员工号
SELECT `employee_id`
FROM `employees`
WHERE `department_id` IN(SELECT `department_id`FROM `departments`WHERE `location_id`=1700
);
#6.查询管理者是King的员工姓名和工资
SELECT `last_name`,`salary`
FROM `employees`
WHERE `manager_id` IN (SELECT `employee_id`FROM `employees`WHERE `last_name`='K_ing'
);
#7.查询工资最高的员工的姓名,要求first_name和last_name显示为一列,列名为 姓.名
SELECT CONCAT(`last_name`,`first_name`) '姓.名'
FROM `employees`
WHERE salary=(SELECT MAX(salary)FROM `employees`
);相关文章:

MySQL——子查询
2023.9.8 相关学习笔记: #子查询 /* 含义: 出现在其他语句中的select语句,称为子查询或内查询 外部的查询语句,称为主查询或外查询分类: 按子查询出现的位置:select后面:仅仅支持标量子查询fro…...
Java学习笔记---多态
面向对象三大特征之一(继承,封装,多态) 多态的应用场景:根据传递对象的不同,调用不同的show方法 一、多态的定义 同类型的对象,表现出的不同形态(对象的多种形态) 二…...

2023-09-10 LeetCode每日一题(课程表 II)
2023-09-10每日一题 一、题目编号 210. 课程表 II二、题目链接 点击跳转到题目位置 三、题目描述 现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites ,其中 prerequisites[i] [ai, bi] ,表示在…...

合并区间【贪心算法】
合并区间 以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。 class Solution {public int[][] merge(int[…...
2023,软件测试人的未来在哪里?
2023年,IT行业出现空前的萧条,首先是年初一开始各大厂像着了魔似的不约而同的纷纷裁员、降薪、奖金包缩水,随之而来的是需求萎缩,HC减少或封锁等等。 而有幸未被列入裁员名单的在职人员,庆幸之余也心有余悸࿰…...
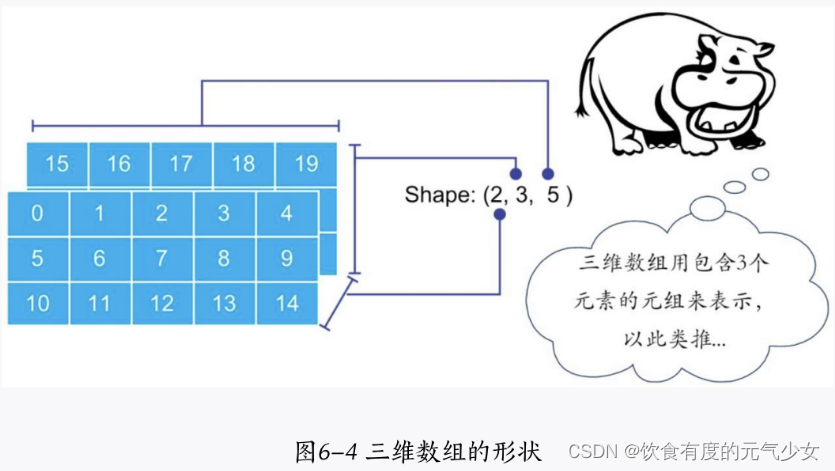
Python中的Numpy向量计算(R与Python系列第三篇)
目录 一、什么是Numpy? 二、如何导入NumPy? 三、生成NumPy数组 3.1利用序列生成 3.2使用特定函数生成NumPy数组 (1)使用np.arange() (2)使用np.linspace() 四、NumPy数组的其他常用函数 (1)np.z…...
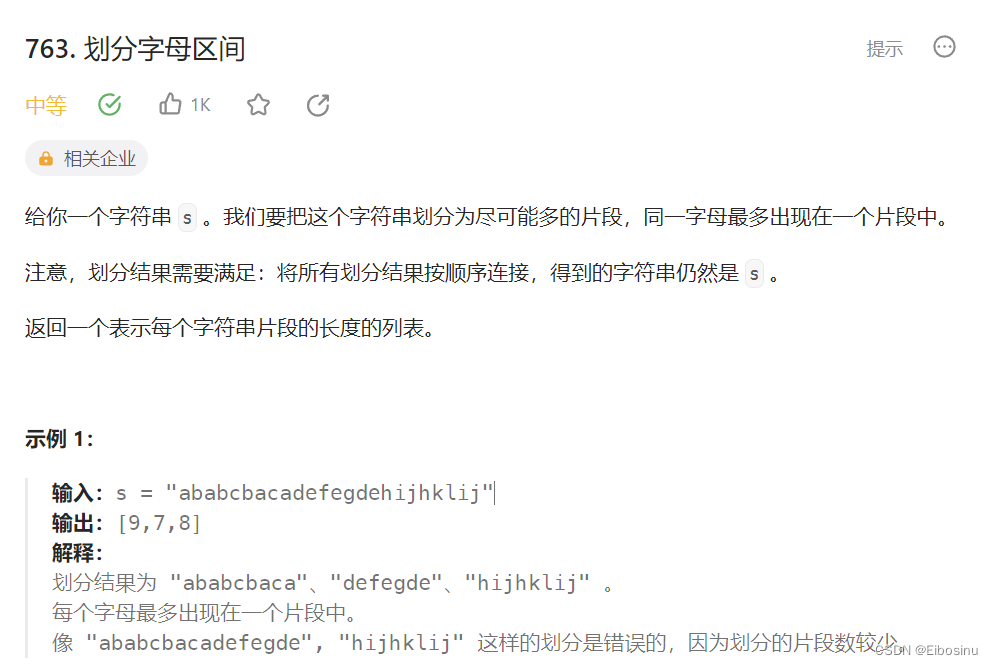
LeetCode刷题笔记【27】:贪心算法专题-5(无重叠区间、划分字母区间、合并区间)
文章目录 前置知识435. 无重叠区间题目描述参考<452. 用最少数量的箭引爆气球>, 间接求解直接求"重叠区间数量" 763.划分字母区间题目描述贪心 - 建立"最后一个当前字母"数组优化marker创建的过程 56. 合并区间题目描述解题思路代码① 如果有重合就合…...

nvidia-smi 命令详解
nvidia-smi 命令详解 1. nvidia-smi 面板解析2. 显存与GPU的区别 Reference: nvidia-smi命令详解 相关文章: nvidia-smi nvcc -V 及 CUDA、cuDNN 安装 nvidia-smi(NVIDIA System Management Interface) 是一种命令行实用程序,用于监控和管理 NVIDIA G…...
函数的返回值)
fork()函数的返回值
在程序中,int pd fork() 是一个典型的 fork() 调用。fork() 函数会创建一个新的进程,然后在父进程中返回子进程的进程ID(PID),在子进程中返回0。所以 pd 的值会根据当前进程是父进程还是子进程而有所不同:…...
)
Stable Diffusion WebUI挂VPN不能跑图解决办法(Windows)
如何解决SD在打开VPN的状态不能运行的问题 在我们开VPN的时候会出现无法生成图片,也无法做其他任何事,这个时候是不是很着急呢? 别急,我这里会说明如何解决。 就像这样,运行半天生成不了图,有时还会出现…...

Android的本地数据
何为本地,即写完之后除非手动修改,否像嘎了一样在那固定死了 有些需求可能也会要求我们去写死数据,因为这需求是一成不变的,那么你通常会用什么方法写死呢? 1. 本地存储-SharedPreferences 此方法可以长时间保存于手…...

android NDK 开发包,网盘下载,不限速
记录下ndk 开发包的地址,分享给大家。 另外有Android studio的下载包, 在另一篇文章 链接:http://t.csdn.cn/JSr9x Android Studio.exe 下载 2023 最新更新,网盘下载_hsj-obj的博客-CSDN博客 主要是19-25,其他的没有…...

【每日一题Day320】LC2651计算列车到站时间 | 数学
计算列车到站时间【LC2651】](https://leetcode.cn/problems/calculate-delayed-arrival-time/) 给你一个正整数 arrivalTime 表示列车正点到站的时间(单位:小时),另给你一个正整数 delayedTime 表示列车延误的小时数。 返回列车实…...
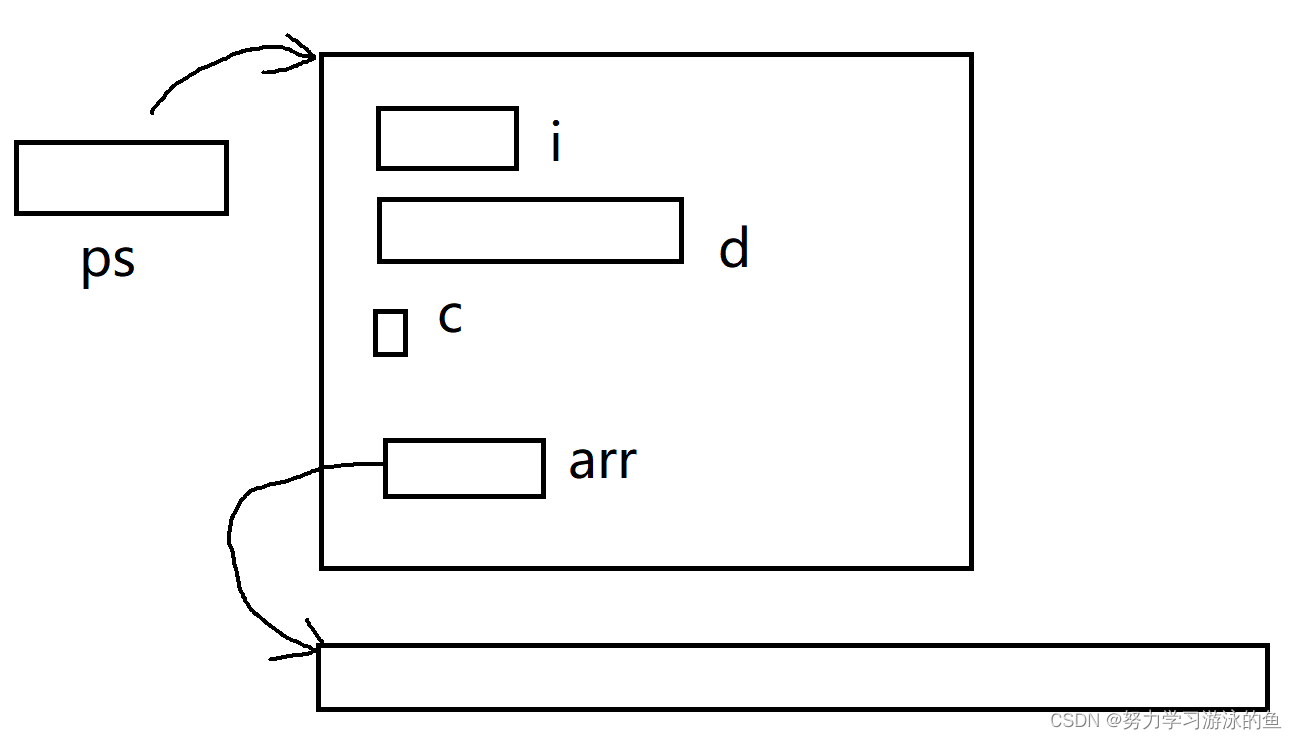
C语言柔性数组详解:让你的程序更灵活
柔性数组 一、前言二、柔性数组的用法三、柔性数组的内存分布四、柔性数组的优势五、总结 一、前言 仔细观察下面的代码,有没有看出哪里不对劲? struct S {int i;double d;char c;int arr[]; };还有另外一种写法: struct S {int i;double …...
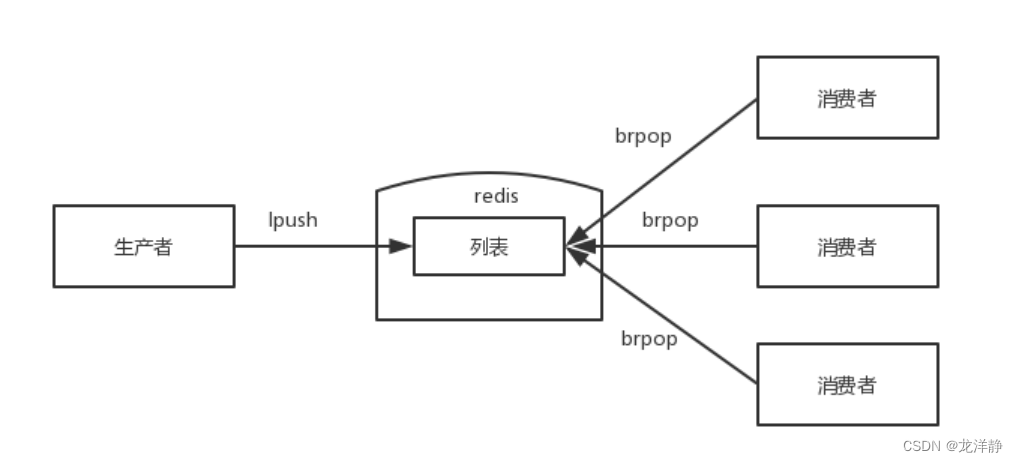
Redis-带你深入学习数据类型list
目录 1、list列表 2、list相关命令 2.1、添加相关命令:rpush、lpush、linsert 2.2、查找相关命令:lrange、lindex、llen 2.3、删除相关命令:lpop、rpop、lrem、ltrim 2.4、修改相关命令:lset 2.5、阻塞相关命令:…...

react拖拽依赖库react-dnd
注:对于表格自定义行可以拖拽和树自定义节点可以拖拽等比较适用,其余的拖拽处理可以使用dragstart,drop等js原生事件来实现 react-dnd使用方法很简单,直接上干货 第一步安装依赖并引入 import { DndProvider } from react-dnd;…...
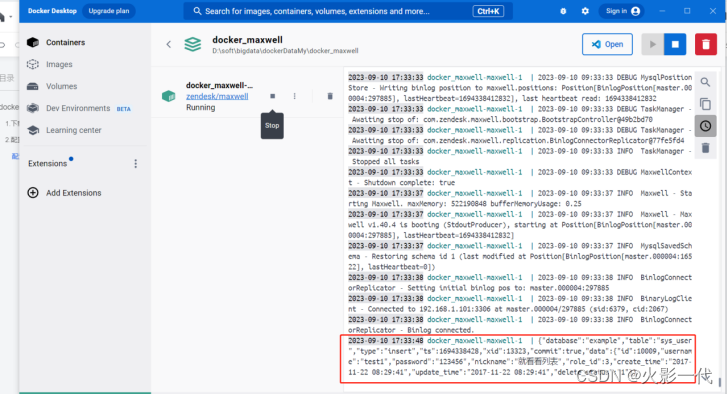
win10环境安装使用docker-maxwell
目的:maxwell可以监控mysql数据变化,并同步到kafka、mq或tcp等。 maxwell和canal区别: maxwell更轻量,canal把表结构也输出了 docker bootstrap可导出历史数据,canal不能 环境 :win10,mysql5…...
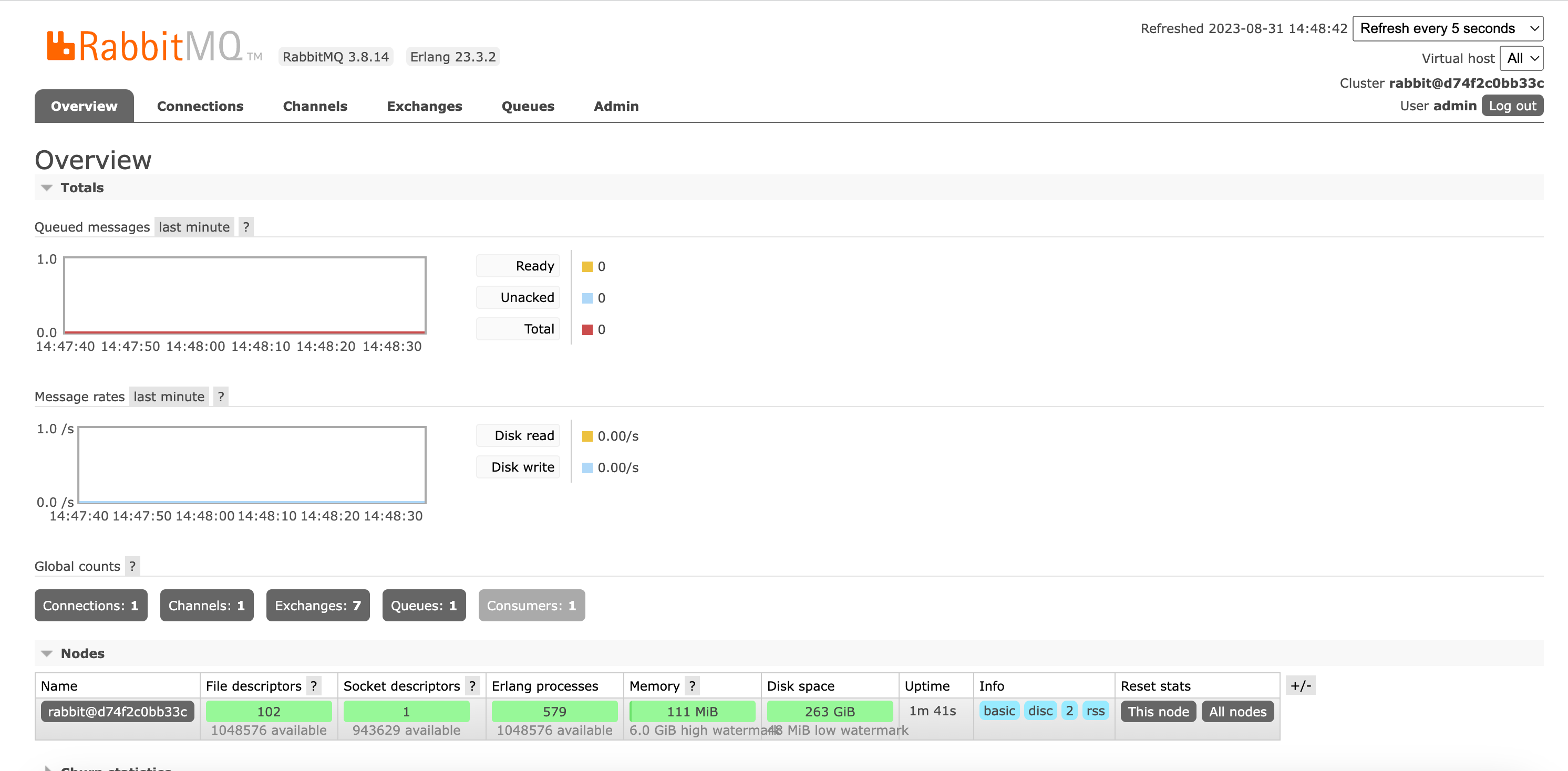
Docker部署RabbitMQ
Docker部署RabbitMQ 介绍 RabbitMQ是一个开源的消息队列系统,它被设计用于在应用程序之间传递消息。它采用了AMQP(高级消息队列协议)作为底层通信协议,这使得它能够在不同的应用程序之间进行可靠的消息传递。 那么,…...
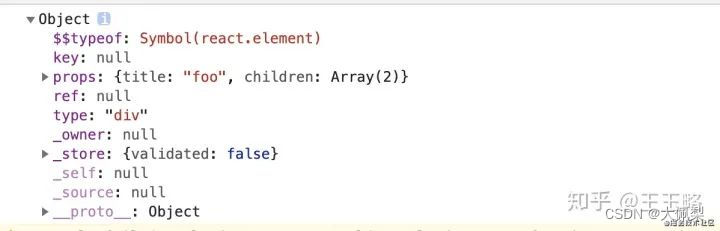
23个react常见问题
1、setState 是异步还是同步? 合成事件中是异步 钩子函数中的是异步 原生事件中是同步 setTimeout中是同步 相关链接:你真的理解setState吗?: 2、聊聊 react16.4 的生命周期 图片 相关连接:React 生命周期 我对 Reac…...

【python基础】——Anaconda下包更新的坑及安装与卸载、及安装后Jupyter Notebook没反应的解决方法
文章目录 前言一、起因:如何一步步走到卸载重装anaconda?二、卸载anaconda二、重新安装anaconda三、关于安装Anaconda后,打开Jupyter Notebook运行代码没反应且in[ ]没有*前言 本文主要用来记录自己近期踩坑的一些复盘。其中坑有: ‘.supxlabel’ 不起作用的解决pip list 与…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...
