《算法竞赛·快冲300题》每日一题:“二进制数独”
《算法竞赛·快冲300题》将于2024年出版,是《算法竞赛》的辅助练习册。
所有题目放在自建的OJ New Online Judge。
用C/C++、Java、Python三种语言给出代码,以中低档题为主,适合入门、进阶。
文章目录
- 题目描述
- 题解
- C++代码
- Java代码
- Python代码
“ 二进制数独” ,链接: http://oj.ecustacm.cn/problem.php?id=1872
题目描述
【题目描述】 Farmer John的农民和他的奶牛们玩一个有趣的数独游戏。
和传统数独一样,这个游戏也是由一个9x9的方格组成,其中又被分为9个3x3的小方格。
不过不同的是,在这个游戏里,只使用二进制数字0和1来填充这些方格。
游戏的目标是尽可能少地改变其中的数字,以使得每行、每列和每个3x3的小方格里都包含偶数个数字1。
例如下面是一个合法的解:
000 000 000
001 000 100
001 000 100
000 110 000
000 110 000
000 000 000
000 000 000
000 000 000
000 000 000
对于给定的初始局面,你需要帮助这些奶牛计算出最小的修改次数。
【输入格式】 输入9行,每行9个字符。
每个字符为0或者1。
【输出格式】 输出一个整数表示答案
【输入样例】
000000000
001000100
000000000
000110000
000111000
000000000
000000000
000000000
000000000
【输出样例】
3
题解
概述题目:给出一个9×9的01矩阵,问最少修改几个数能使每行、每列以及每个九宫格中1的个数均为偶数。在样例中,一种修改方法是把上面两个1和右下角的1改为0,一共改3次。
如何得到最小修改次数?先试试暴力搜索,用DFS编码,把所有可能的修改都尝试一遍。比较不同方法的修改次数,其中最少修改次数就是答案。有多少种可能的修改?有9×9=81个格子,每个格子有两种改法(改为0或1),共有 2 81 2^{81} 281种修改方法。 2 81 2^{81} 281显然太大了,不过加上剪枝之后,能优化很多。
还有另外一种暴力法。共81个格子,最少修改次数是1,最多是81。从小到大逐一判断修改次数。先试只改一个格子,共81种修改方法,验证每种方法能不能达到目标;如果不行,再试改2个格子,共81×80种修改方法;等等。读者可以证明,这个暴力法和上面的暴力法的计算量差不多。可以用二分法优化,但只是把81优化到log81,其它的计算量仍然巨大。
本题并不是求共有多少种修改方法,而是求最少修改次数。这种最优性问题,考虑用DP求解。
下面模拟修改过程。设左上角坐标是(0,0),右下角坐标是(8,8)。按从左到右,从上到下的顺序修改每个格子。从左上角(0,0)开始,先改第0行,再改第1行,一直到第8行。
题目要求每行、每列、每3×3的方格都包含偶数个1,按这三个要求设计DP。DP的步骤是:
(1)第0行,用DP记录第0行的9列格子的最少修改次数,需要验证第0行是否有偶数个1。
(2)第1行,用DP记录第0~1行的9列格子的最少修改次数,需要验证第1行是否有偶数个1。
(3)第2行,用DP记录记录第0~2行的9列格子的最少修改次数,需要验证第2行是否有偶数个1,并且验证三个3×3的九方格是否有偶数个1。
等等,一直到第8行。
每个小格子里面是0或者1,容易联想到用状态压缩DP。定义状态dp[][][][][],dp[r][c][mask][sub][row]的含义是:
(1)当前到达位置(r,c),即第r行,第c列,代码中r和c的范围是0~8。
(2)mask表示每列数字1出现的次数。设当前在第r行,统计0~r行的每一列的1的个数是否为偶数。为了简化用状态压缩,mask是一个9位的二进制数,每一位表示每一列的数字1出现的次数,奇数次为1,偶数次为0。例如000000001,表示最后一列(第8列)有奇数个1,其他列都是偶数个1。
(3)sub表示每三列数字1出现的次数。同样用状态压缩,sub是一个3位的二进制数,3位分别表示第02列、第35列、第6~8列的数字1出现的次数,奇数次为1,偶数次为0。
(4)row表示当前行数字1出现次数,奇数次为1,偶数次为0。
DP用dfs()编程,从第0行第0列开始逐一处理第(r,c)位置的小格子,直到最后的第8行第8列。每个格子有两种改动方法,改为1或0。
(1)改为1,修改次数ans:
ans = !a[r][c] + dfs(r, c+1, mask ^ (1<<c), sub^(1<<(c/3)), !row);
!a[r][c]:若原来a[r][c] = 0,现在改为a[r][c] = 1,修改次数ans+1;若原来a[r][c] = 1,现在仍有a[r][c] = 1,修改次数不变。两种情况下增加的修改次数都是!a[r][c]。
c+1:继续dfs,往右走一列。
mask ^ (1<<c):第c列多了一个1,更新第c列的1的数量为新的奇或偶。
sub^(1<<(c/3)):更新每三列的奇偶,例如c = 2时,c/3 = 0,表示c在前三列中,更新前三列1的数量情况。
!row:更新当前行中1的数量的奇偶,由于这一行多了一个1,新的row和原来相反。
(2)改为0,修改次数ans:
ans = min(ans, a[r][c] + dfs(r, c + 1, mask, sub, row));
a[r][c]:若原来a[r][c] = 1,现在改为a[r][c] = 0,则修改次数ans+1;若原来a[r][c] = 0,修改次数不变。两种情况下增加的修改次数都是a[r][c]。
c+1:继续dfs,往右走一列;
mask、sub、row:因为(r,c)这个格子变成了0,没有增加1,所以都不变。
其他处理见代码。
【重点】 状态压缩DP 。
C++代码
#include<bits/stdc++.h>
using namespace std;
const int INF = 999;
bool a[9][9]; //存方格矩阵,行标0~8,列标0~8
int dp[9][9][1<<9][1<<3][2]; //dp[r][c][mask][sub][row]
int dfs(int r, int c, int mask, int sub, bool row){if(r == 9) //0-8行已经填满,必须保证mask=0,sub=0,row=0return (!mask && !sub && !row) ? 0 : INF;if(c == 9){ //0-8列已经填完if(row) return INF; //1、保证本行偶数个if(r%3 == 2 && sub) return INF; //2、保证每三行统计一下每三列数字1出现次数为偶数个return dfs(r + 1, 0, mask, sub, 0); //3、下一行}int& ans = dp[r][c][mask][sub][row]; //ans是dp的别名,把下面的ans改成dp,结果一样if(ans != -1) return ans; //记忆化ans = !a[r][c] + dfs(r, c+1, mask ^ (1<<c), sub^(1<<(c/3)), !row);//a[r][c]设置为1。 若原来a[r][c]=0,ans+1ans = min(ans, a[r][c] + dfs(r, c + 1, mask, sub, row));//a[r][c]设置为0。 若原来a[r][c]=1,ans+1return ans;
}
int main(){for(int i = 0; i < 9; i++){string s; cin >> s;for(int j = 0; j < 9; j++)a[i][j] = (s[j] == '1'); //存到 a[0][0]~a[8][8]}memset(dp, -1, sizeof(dp));cout<<dfs(0, 0, 0, 0, 0)<<endl;
}
Java代码
import java.util.*;
import java.io.*;
public class Main {private static final int INF = 999;private static boolean[][] a; // 存方格矩阵,行标0~8,列标0~8private static int[][][][][] dp; // dp[r][c][mask][sub][row]private static int dfs(int r, int c, int mask, int sub, int row) {if (r == 9) // 0-8行已经填满,必须保证mask=0,sub=0,row=0return (mask == 0 && sub == 0 && row == 0) ? 0 : INF; if (c == 9) { // 0-8列已经填完if (row==1) return INF; // 1、保证本行偶数个if (r % 3 == 2 && sub != 0) return INF;
// 2、保证每三行统计一下每三列数字1出现次数为偶数个return dfs(r + 1, 0, mask, sub, 0); // 3、下一行}if (dp[r][c][mask][sub][row] != -1) // 记忆化return dp[r][c][mask][sub][row];int ans;ans = (!a[r][c]?1:0) + dfs(r, c+1, mask ^ (1<<c), sub^(1<<(c/3)), 1 - row);ans = Math.min(ans, (a[r][c]?1:0) + dfs(r, c + 1, mask, sub, row));dp[r][c][mask][sub][row] = ans;return ans;}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);a = new boolean[9][9];for (int i = 0; i < 9; i++) {String s = scanner.next();for (int j = 0; j < 9; j++) a[i][j] = (s.charAt(j) == '1'); // 存到 a[0][0]~a[8][8] }dp = new int[9][9][1 << 9][1 << 3][2];for (int[][][][] rows : dp) for (int[][][] row : rows) for (int[][] sub : row) for (int[] arr : sub) Arrays.fill(arr, -1);System.out.println(dfs(0, 0, 0, 0, 0));}
}
Python代码
INF = 999
a = [[False for j in range(9)] for i in range(9)] # 存方格矩阵,行标0~8,列标0~8
dp = [[[[[-1 for k in range(2)] for j in range(1 << 3)] for i in range(1 << 9)] for c in range(9)] for r in range(9)]
def dfs(r, c, mask, sub, row):if r == 9: # 0-8行已经填满,必须保证mask=0,sub=0,row=0return 0 if not mask and not sub and not row else INFif c == 9: # 0-8列已经填完if row: return INF # 1、保证本行偶数个if r % 3 == 2 and sub: return INF # 2、保证每三行统计一下每三列数字1出现次数为偶数个return dfs(r + 1, 0, mask, sub, False) # 3、下一行if dp[r][c][mask][sub][row] != -1:return dp[r][c][mask][sub][row] # 记忆化
ans = dfs(r, c+1, mask ^ (1 << c), sub ^ (1 << (c // 3)), not row) + (not a[r][c])
# a[r][c]设置为1。若原来a[r][c]=0,ans+1
ans = min(ans, dfs(r, c+1, mask, sub, row) + a[r][c])# a[r][c]设置为0。若原来a[r][c]=1,ans+1dp[r][c][mask][sub][row] = ans # 存储结果return ans
for i in range(9):s = input().strip()for j in range(9): a[i][j] = s[j] == '1' # 存到 a[0][0]~a[8][8]
print(dfs(0, 0, 0, 0, False))相关文章:

《算法竞赛·快冲300题》每日一题:“二进制数独”
《算法竞赛快冲300题》将于2024年出版,是《算法竞赛》的辅助练习册。 所有题目放在自建的OJ New Online Judge。 用C/C、Java、Python三种语言给出代码,以中低档题为主,适合入门、进阶。 文章目录 题目描述题解C代码Java代码Python代码 “ 二…...
CnosDB 签约京清能源,助力分布式光伏发电解决监测系统难题。
近日,京清能源采购CnosDB,升级其“太阳能光伏电站一体化监控平台”。该平台可以实现电站设备统一运行监控,数据集中管理,为操作人员、维护人员、管理人员提供全面、便捷、差异化的数据和服务。 京清能源集团有限公司(…...

汇编:lea 需要注意的一点
lea和mov的效用上不一样,如果当前%rsi的值是0, lea 0x28(%rsi),%rax ,这个只是计算一个地址,而不是去做地址访问。 mov 0x8(%rsi),%rsi,而这个mov,在计算完地址,还要访问内存地址。如果rsi是0&a…...
SQL语言的分类:DDL(数据库、表的增、删、改)、DML(数据的增、删、改)
数据库管理系统(数据库软件)功能非常多,不仅仅是存储数据,还要包含:数据的管理、表的管理、库的管理、账户管理、权限管理等。 操作数据库的SQL语言,基于功能,划分为4类: 1、数据定…...

微信小程序精准扶贫数据收集小程序平台设计与实现
摘 要 近些年以来,随着我国的互联网技术的不断进步,计算机科学技术的发展也在不断的快速发展。在当下“互联网”的带动下,我国的各行各业,上到政府机关下到小微企业都通过互联网的发展带动取得了很好的发展势头。我国这两年来通过…...

PostgreSQL 流复制搭建
文章目录 前言1. 配置环境1.1 环境介绍1.2 主库白名单1.3 主库参数配置 2. 流复制搭建2.1 备份恢复2.2 创建复制用户2.3 参数修改2.4 启动并检查2.5 同步流复制2.6 同步复制级别 3. 流复制监控3.1 角色判断3.2 主库查看流复制3.3 延迟监控3.4 备库查询复制信息 前言 PostgreSQ…...

机器学习笔记之最优化理论与方法(十)无约束优化问题——共轭梯度法背景介绍
机器学习笔记之最优化理论与方法——共轭梯度法背景介绍 引言背景:共轭梯度法线性共轭梯度法共轭方向共轭VS正交共轭方向法共轭方向法的几何解释 引言 本节将介绍共轭梯度法,并重点介绍共轭方向法的逻辑与几何意义。 背景:共轭梯度法 关于…...

Mybatis核心对象及工作流程
目录 一、mybatis核心对象 (1)SqlSession对象直接操作数据库 (2)SqlSession对象通过代理对象操作数据库 二、mybatis工作流程 一、mybatis核心对象 (1)SqlSessionFactoryBuilder SqlSession工厂构建者对…...
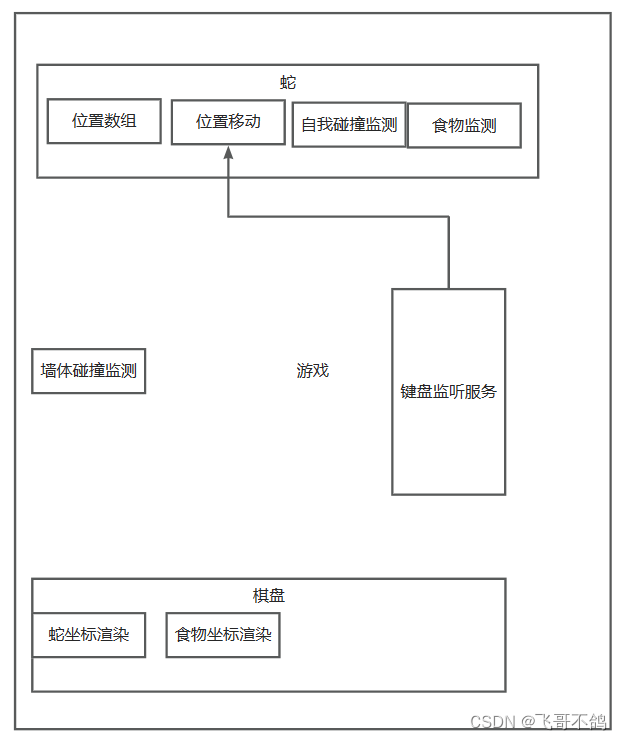
无swing,高级javaSE毕业之贪吃蛇游戏(含模块构建,多线程监听服务),已录制视频
JavaSE,无框架实现贪吃蛇 B站已发视频:无swing,纯JavaSE贪吃蛇游戏设计构建 文章目录 JavaSE,无框架实现贪吃蛇1.整体思考2.可能的难点思考2.1 如何表示游戏界面2.2 如何渲染游戏界面2.3 如何让游戏动起来2.4 蛇如何移动 3.流程图…...
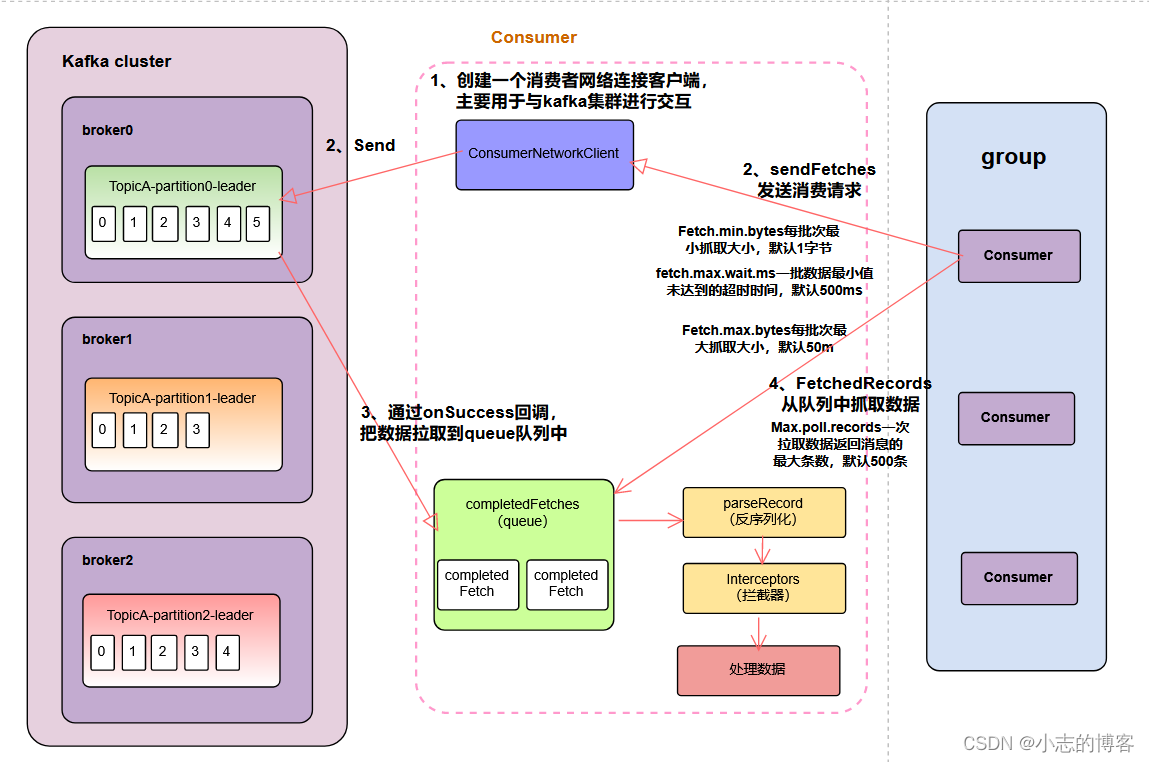
Kafka3.0.0版本——消费者(消费者组详细消费流程图解及消费者重要参数)
目录 一、消费者组详细消费流程图解二、消费者的重要参数 一、消费者组详细消费流程图解 创建一个消费者网络连接客户端,主要用于与kafka集群进行交互,如下图所示: 调用sendFetches发送消费请求,如下图所示: (1)、Fet…...

算法通关村-----位运算在海量元素中查找重复元素的妙用
用4KB内存寻找重复元素 问题描述 给定一个数组,包含从1到N的整数,N最大为32000,数组可能还有重复值,且N的取值不定,若只有4KB内存可用,如何打印数组中所有的重复元素。 问题分析 Java中存储整数使用int…...

RabbitMQ: Publish/Subscribe结构
生产者 package com.qf.mq2302.publishSub;import com.qf.mq2302.utils.MQUtils;import com.rabbitmq.client.Channel; import com.rabbitmq.client.Connection;public class EmitLog {private static final String EXCHANGE_NAME "logs";public static void main…...

单片机-蜂鸣器
简介 蜂鸣器是一种一体化结构的电子讯响器,采用直流电压供电 蜂鸣器主要分为 压电式蜂鸣器 和 电磁式蜂鸣器 两 种类型。 压电式蜂鸣器 主要由多谐振荡器、压电蜂鸣片、阻抗匹配器及共鸣箱、外壳等组成。多谐振荡器由晶体管或集成电路构成,当接通电源后&…...

华为云云耀云服务器L实例评测 | 分分钟完成打地鼠小游戏部署
前言 在上篇文章【华为云云耀云服务器L实例评测 | 快速部署MySQL使用指南】中,我们已经用【华为云云耀云服务器L实例】在命令行窗口内完成了MySQL的部署并简单使用。但是后台有小伙伴跟我留言说,能不能用【华为云云耀云服务器L实例】来实现个简单的小游…...

Android——数据存储(二)(二十二)
1. SQLite数据库存储 1.1 知识点 (1)了解SQLite数据库的基本作用; (2)掌握数据库操作辅助类:SQLiteDatabase的使用; (3)可以使用命令操作SQLite数据库; …...

appium环境搭建
一.appium环境搭建 1.python3 python3的下载安装这里就不多做介绍了,当然你也可以选择自己喜欢的语音,比如java… 2.jdk 1)下载地址 官网(需登录账号): https://www.oracle.com/java/technologies/downloads/ 百度网盘&…...
十五、Webpack打包图片-js-Vue、Label命令、resolve模块解析
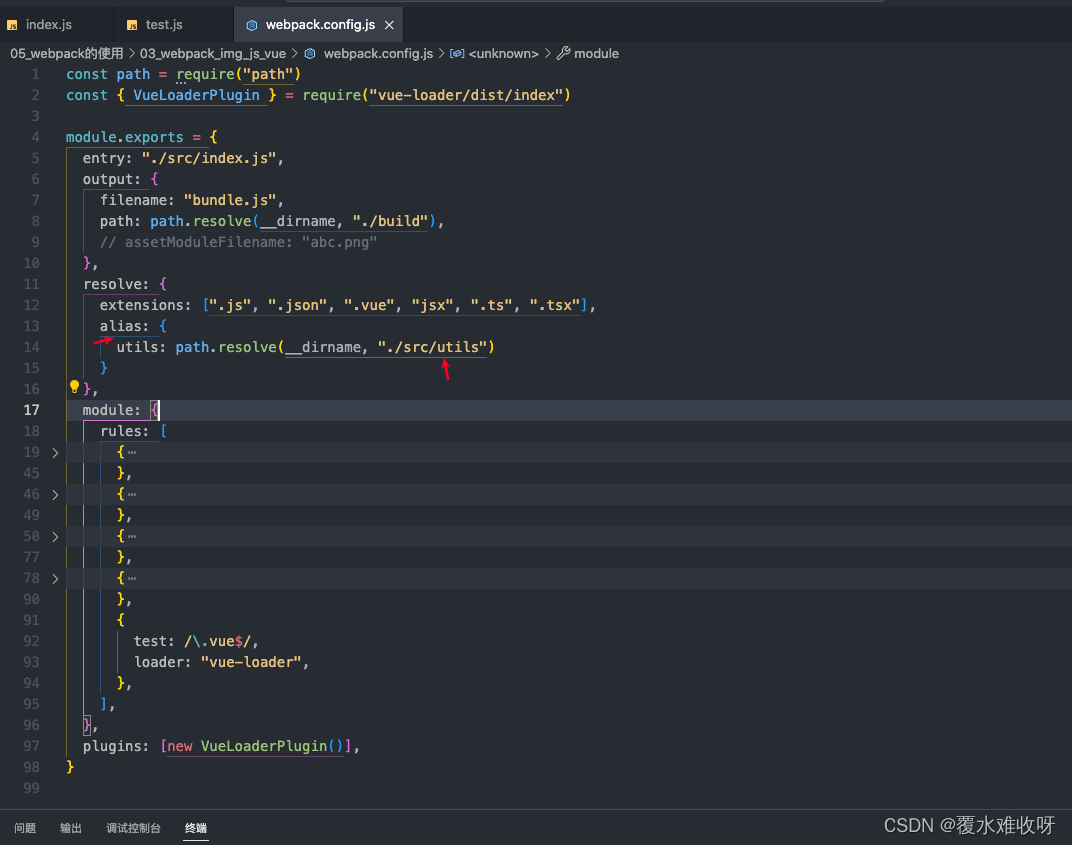
一、webpack打包图片 (1)加载图片案例准备 为了演示我们项目中可以加载图片,我们需要在项目中使用图片,比较常见的使用图片的方式是两种: img元素,设置src属性;其他元素(比如div&…...

ARM指令集--数据处理指令
数据处理指令:数学运算,逻辑运算 立即数 立即数的本质 就是包含在指令当中的数,属于指令的一部分 立即数的优点:取指的时候就可以将其读取到CPU,不用单独去内存读取,速度快 立即数的缺点:不…...

Excel embed into a webpage
无法编辑嵌入式 Excel 网页版 工作簿,但具有适当权限的人员可能能够在 Excel 中打开嵌入的工作簿,他们可以在其中编辑数据。 通过制作一个浏览器,打开并编辑它 https://onedrive.live.com/embed? resid5FC97855340825A9%21135& aut…...
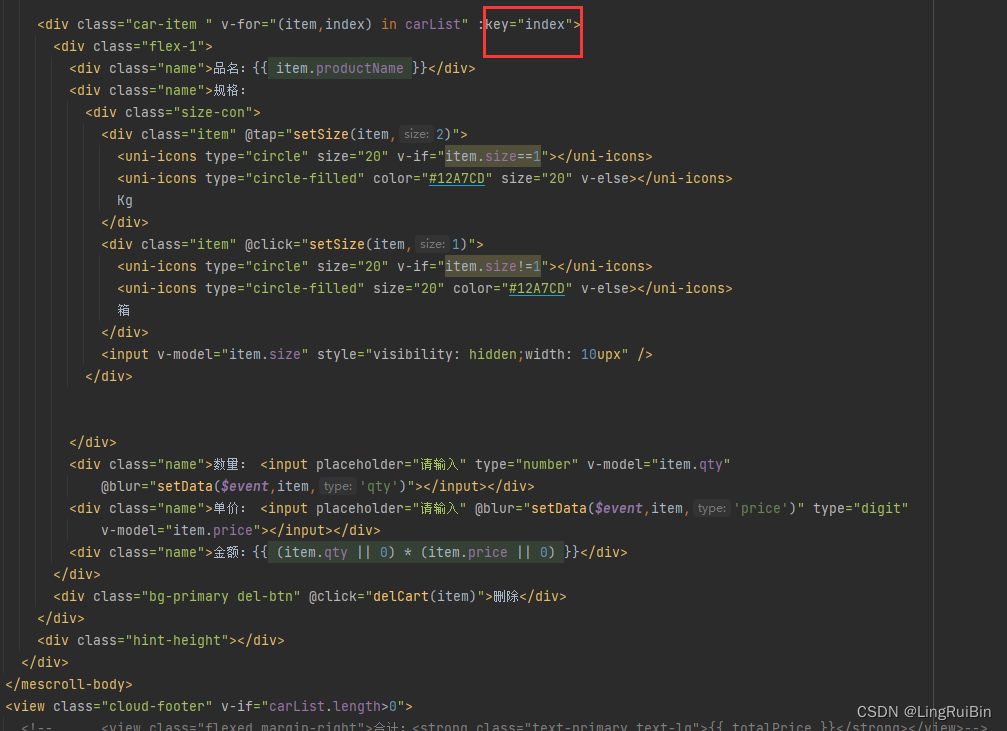
uniapp点击事件在小程序中无法传参
这个问题很是神奇,第一次遇到。在h5中,点击事件可以正常传参,打包小程序后确失效了。 修改:for循环中的key,使用 index就好了...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
