Matlab如何导入Excel数据并进行FFT变换
如果你发现某段信号里面有干扰,想要分析这段信号里面的频率成分,就可以使用matlab导入Excel数据后进行快速傅里叶变换(fft)。
先直接上使用方法,后面再补充理论知识。
可以通过串口将需要分析的数据发送到串口助手,注意,串口助手复制数据,是你接收了多少,就能复制多少。
将接收到的数据放到Excel表格中,用一列就可以了,不必给数据列表头起名字。

注意:
为了方便进行 FFT 运算,通常数据数量 取 2 的整数次方。可以加快matlab的分析速度,不是也关系不大。
另外,要去掉这一列数据中的空格,否则matlab无法分析出正确结果,选中这一列,查找全部空格,然后在某一个选中的空格上右键删除行即可删除所有空格。
打开matlab软件,点击导入数据

等待一段时间(根据电脑配置而不同)后,就会出现如下界面
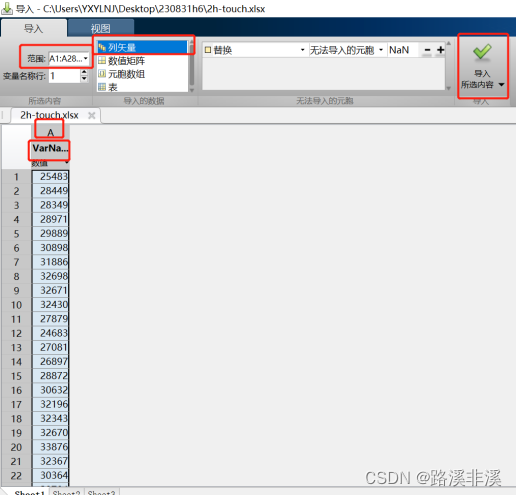
范围:虽然将Excel中的所有数据都导入了,但是可以选择数据范围进行分析,这里就可以选择,Am:An,表示A列的第m到第n个数据。
列矢量:因为只导入了一列,所以选择列矢量即可,网上好多教程都是让导入两列,然后选择数值矩阵,其实没有必要。
VarName:导入一列数据时,该列向量的变量名就是VarName,多个的话就是VarName1、VarName2、VarName3……最多到VarName9,所以,如果超过VarName9,就不能再用VarName这个名称了。不过,我们也可以双击这里的名称,然后修改。
一般情况下,数据导入后,只需要选择性地更改名称即可,其他都是默认选择。
确认无误后,点击绿色对钩导入所选内容,当出现蓝色字提示,就表示数据已经导入了
此时,可以在工作区看到该变量名

到了这里,数据已经被导入了。
接下来,就可以进行傅里叶变换,并绘制出幅频图了。
点击新建脚本并保存,然后在脚本中输入以下程序
Fs = 2000;
Y = fft(VarName1);
L = length(Y);
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
f = Fs*(0:(L/2))/L;
plot(f,P1);
axis([0,Fs/2,0,200]);
title('frequency-domain');
xlabel('f(Hz)');
ylabel('频率成分的幅值');
其中,Y = fft(VarName1);这里的VarName1就是刚才导入的变量名,如果是别的名称,对应起来即可。
选中这些程序,然后右键执行所选内容

稍作等待,就会出现幅频图
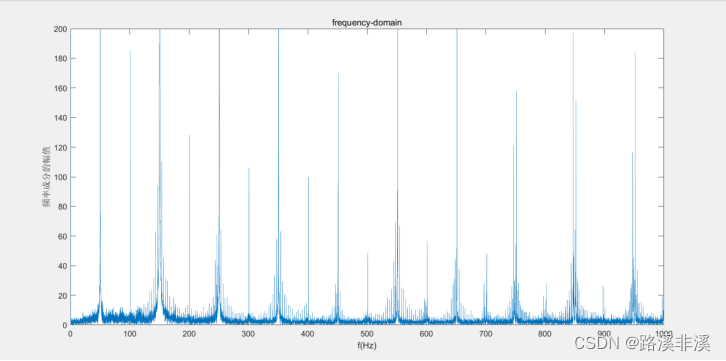
可以看到,这个信号里面,是有很多工频干扰的,而且,干扰的范围还不小。
至此,整个使用过程已结束。
理论知识补充
以上的过程其实就是涉及到DSP数字信号处理的知识。
接下来补充一下理论知识,帮助更好地理解以上内容。
首先,什么是傅里叶变换?
傅立叶变换是一种分析信号的方法,它可分析信号的成分,也可用这些成分合成信号。
想要更好地理解这个问题,可以参考:
傅里叶分析之掐死教程(完整版)更新于2014.06.06 - 知乎
这篇文章形象地讲解了什么是傅里叶级数和傅里叶变换。
摘录精华如下:

简单点来说,就是任一函数都可以展成三角函数的无穷级数
其次,什么是FFT?
FFT 是离散傅立叶变换的快速算法,可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。这就是很多信号分析采用 FFT 变换的原因。另外,FFT 可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。
了解了什么是FFT,就能更好地理解一些问题了。
比如,为什么信号有干扰之后数值会变大?
一般,我们看电流或者电压强度,都是看幅值,本来信号值是5,可是采到的却是48,显然太大了,此时,就是因为有其他频率的干扰叠加在了信号上面,导致幅值增大。如果干扰很大,幅值就会增大很多。
所以,就要搞清楚是什么频率的干扰波叠加在信号上面,因此就可以进行fft变换来分析。
幅频图表示什么含义?
横坐标是连续的频率值,纵向就是各频率信号的幅度值,也就是叠加在原始信号上的强度。
注意:我在上面提供的程序所出来的图,因为做了纵向量纲的校准,所以显示的幅值就是频率的实际幅值。
接下来就要重点讲解一下这段程序。
首先,可以看看这几个视频,看完你就会恍然大悟。
NO.12 傅里叶变换频谱图你必须知道的_哔哩哔哩_bilibili
Fs = 2000;
Y = fft(VarName1);
L = length(Y);
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
f = Fs*(0:(L/2))/L;
plot(f,P1);
axis([0,Fs/2,0,200]);
title('frequency-domain');
xlabel('f(Hz)');
ylabel('频率成分的幅值');
针对这个程序,一句一句地分析。
Fs = 2000;
一开始,这里面有个采样率Fs,是我最不能理解的部分,因为真的很难理解。
我看了很多网络上的讲解,都没有能够讲解Fs这个怎么来的。
而且,这个Fs真的很关键,非常关键。我在实际操作中,只要Fs变了,频率值就变了,比如,原本是50Hz的干扰,如果Fs减半,频率也会减半到25Hz去显示,这样,就会误导我们,到底是什么频率的干扰?非常容易造成误判。
2000的采样率
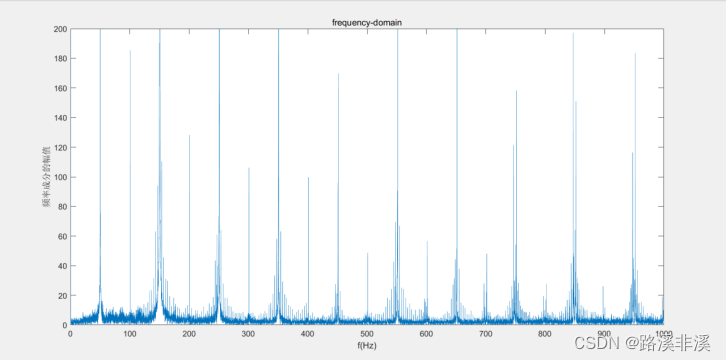
1000的采样率

很明显,虽然总体趋势没变,但是频率从原来的50Hz干扰,变到了25Hz的干扰。
这就已经对我们造成了严重的误导。因为就会导致后面一系列的连锁错误。
这么重要的问题,不知道为什么大家都不讲清楚。
由上面的分析可知,只有唯一一个确定的Fs才能够保证我们的分析结果是正确的。
那这个Fs值到底是多少呢?
这个Fs到底是怎么确定的呢?
一开始,我有好多疑问,Fs是matlab分析所需要的,可以任意取值的吗?上面我们已经证明了并不是随便取值的。
然后,我又想,难道是跟原始信号的频率有关?原始信号有无数个频率叠加,不可能是由它们来确定的。而且,叠加之后的频率也没法确定。
那就是ADC的采样频率?有点接近了,不过我查了一下程序,发现ADC的采样频率对不上。
再理一理思路,有一个原始信号,叠加了很多的干扰信号,我用ADC来采集,采集之后通过串口一个一个地发送到PC,ADC的采样速度比串口的速度要快。假设原始信号最大频率是1000Hz,ADC按照2000Hz去采,采了3000个点,可是串口只每隔2个点上传一次,那采样率就是1000?
最终,我想明白了,我要分析的数据是怎么来的,就看它的最终获取频率。
只需要看最终输出,不管中间经历了多少路径,只看最后收到了多少原始数据,不经过任何处理。
串口是每500us发送一个数据,也就是说,采样率是2000,这是我最终得到的数据采样率,也就是我要分析的数据的采样率。
有三种方式可以验证:
- 更改串口的发送频率来验证;
- 看串口是不是1秒钟接收了那么多数据;
- 可以输入一个有明显幅度的特定频率信号,然后验证设定的采样率下,频率显示是否正确。
其中,第三种方式,是最直观最准确的,推荐使用。
Y = fft(VarName1);
傅里叶变换
将时域数据转换成频域数据,也就是一个一个的频率点,是根据欧拉公式,使用复数来表示的。
时域数据

频域数据

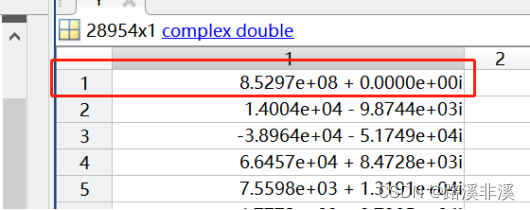
这里是用科学计数法来表示的。
第一个数就是实数,第二个数就是虚数,后面的i是虚数单位。
时域数据和频域数据的数量是一样的。N 个采样点,经过 FFT 之后,就可以得到 N 个点的FFT结果。
频域数据具有对称性和周期性。
L = length(Y);
获取数据的长度,也就是数量。
P2 = abs(Y/L);
P1 = P2(1:L/2+1);%这里加1是为了包含对称性数据的中间数据
P1(2:end-1) = 2*P1(2:end-1);
上面说了,频域数据里就是一个一个频率点的复数表示,这些频率点的强度是多少呢?直接对复数值取模即可,也就是abs(Y);
假设 FFT之后某点 n 用复数 a+bi 表示,那么这个复数的模就是:
![]()
为什么上面要除以L呢?P2 = abs(Y/L);
其实,不是为了除以L,是想除以L/2。
为什么?
FFT 之后结果就是一个为 N 点的复数。每一个点就对应着一个频率点。这个点的模值,就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢?假设原始信号的峰值为 A,那么 FFT 的结果的每个点(除了第一个点直流分量之外)的模值就是 A 的 N/2 倍。 而第一个点就是直流分量,它的模值就是直流分量的 N 倍。
根据这段话可知:点的模值=原始信号的模值*(N/2),所以,点的模值/(N/2),就能获取该频率信号实际的幅度值。
以上是先除以L,再P1(2:end-1) = 2*P1(2:end-1);这里乘以2,就是为了换算成实际的幅值。
而且,P1(2:end-1) = 2*P1(2:end-1);这里从第2点开始是为了将直流分量去掉,因为直流分量不用乘以2,直接除以L即可。这里的end表示最后一个元素索引:

为什么去掉最后一个点,只到end-1。
因为end-1表示对称的最中心数据,该频率点的波形不显示。
说明如下:
fs=1000; %设置采样频率 1k
N=1024; %采样点数
n=0:N-1;
t=0:1/fs:1-1/fs; %时间序列
f=n*fs/N; %频率序列
x1=sin(2*pi*70*t); %噪声
x2=sin(2*pi*200*t); %信号
x3=sin(2*pi*500*t); %信号
x=x1+x2+x3; %信号混合
subplot(311);
plot(t,x); %绘制原始信号
xlabel('时间');
ylabel('幅值');
title('原始信号');
可以看到,500Hz的频率图像没有显示出来。

为什么这里只取一半的值?
要注意,这里并不是取一半的值,而是只取一半的点来分析。这是因为傅里叶变换后的数据具有对称性,后一半的数据不具备实际意义。

接下来的这句f = Fs*(0:(L/2))/L;就是为了适应这一点,这句话实际结果就是0—Fs/2,这句话不是为了取一半的点,而是为了取一半的频率。
FFT 之后结果就是一个为 N 点的复数。每一个点就对应着一个频率点。第一个点表示直流分量(即 0Hz),而最后一个点 N 的再下一个点(实际上这个点是不存在的,这里是假设的第 N+1 个点,可以看做是将第一个点分做两半分,另一半移到最后)则表示采样频率 Fs,这中间被 N-1 个点平均分成 N 等份,每个点的频率依次增加。
其实,可以从另一个角度来理解,那就是著名的奈奎斯特采样定律:只要采样频率大于或等于有效信号最高频率的两倍,采样值就可以包含原始信号的所有信息,被采样的信号就可以不失真地还原成原始信号。
一个模拟信号,经过 ADC 采样之后,就变成了数字信号。采样定理告诉我们,采样频率要大于信号频率的两倍。
我们这里的采样率是Fs,所以最大只能采到Fs/2的最大频率信号,那么,高于Fs/2的频率部分其实是没有意义的。
另外,根据上面的频率分布可知道,Fn 所能分辨到频率为 Fs/N,如果采样频率 Fs 为 1024Hz,采样点数为1024点,则可以分辨到 1Hz。1024Hz 的采样率采样 1024 点,刚好是 1 秒,也就是说,采样 1 秒时间的信号并做 FFT,则结果可以分析到 1Hz,如果采样 2 秒时间的信号并做 FFT,则结果可以分析到 0.5Hz。如果要提高频率分辨力,则必须增加采样点数,也即采样时间。
所以,如果对分辨率要求不高,就可以少取一些数据。对分辨率要求高,就需要多取一些数据。
由于 FFT 结果的对称性,通常我们只使用前半部分的结果,即小于采样频率一半的结果。
FFT结果的是存在对称性的,这是由FFT计算中隐含的复数运算处理、以及计算是对周期性离散处理(时域、频域转换) 等带来的特性,一般使用时不用详究,只需要知道存在这个特性即可,数据也只需要用任意一半即可(普遍采用前一半)。
具体原因,可自行查找资料。
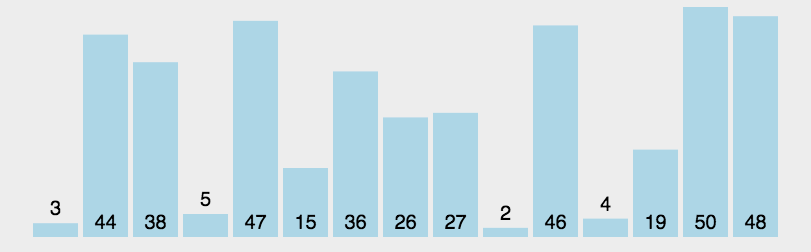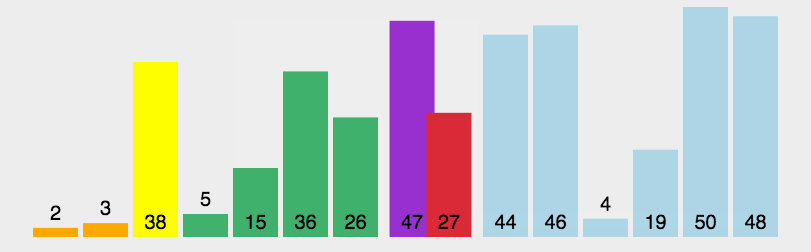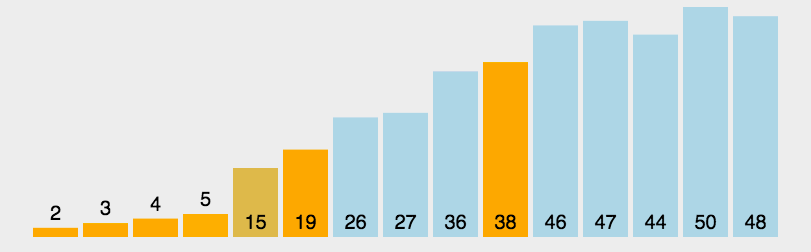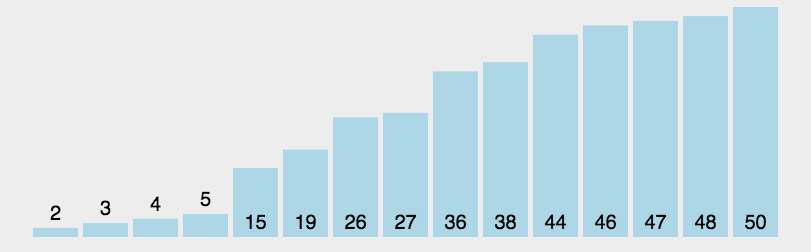
对称性示例:

注意,对称性不包含第一个直流分量。
附上手写信号测试:
ts = 0:0.01:10;
sig = sin(2*pi*ts) + 5*sin(2*pi*10*ts);
Fs = 100;
Y = fft(sig);
L = length(Y);
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
f = Fs*(0:(L/2))/L;
plot(f,P1);
%axis([0,1000,0,200]);
title('frequency-domain');
xlabel('f(Hz)');
ylabel('频率成分的幅值');
相关文章:

Matlab如何导入Excel数据并进行FFT变换
如果你发现某段信号里面有干扰,想要分析这段信号里面的频率成分,就可以使用matlab导入Excel数据后进行快速傅里叶变换(fft)。 先直接上使用方法,后面再补充理论知识。 可以通过串口将需要分析的数据发送到串口助手&a…...
华为mate60 上线 媒介盒子多家媒体报道
为什么你的品牌营销不见效?如何能推动品牌破圈?让媒介盒子给你一些启发。本期盒子要跟大家分享地新机上市,数码科技行业企业该如何做线上宣传。 HUAWEI Mate 60系列8月29日官宣发布,出色的拍照功能、强大的性能表现和持久的续航能…...

Java知识总结(持续更新)
一、JDK、JRE、JVM三者之间的关系? 1. **JDK (Java Development Kit)**: JDK 是 Java 开发工具包,它包含了用于开发 Java 应用程序的所有必要工具和库。这包括 Java 编译器(javac)、Java 核心类库、开发工具&#x…...

缓存技术:加速应用,提高用户体验
本文总结前期某个系统中使用到的缓存使用经验—仅此而已,效果还不错。 缓存技术在系统架构设计中扮演着至关重要的角色,它不仅可以显著提高系统的性能,还可以改善用户体验。在本文章中,我们将探讨不同类型的缓存、缓存失效以及缓存淘汰等关键概念,帮助在后期的架构设计中…...

MySQL中分区与分表的区别
MySQL中分区与分表的区别 一、分区与分表的区别 分区和分表是在处理大规模数据时的两种技术手段,尽管它们的目标都是提升系统的性能和数据管理的效率,但它们的实现方式和应用场景略有不同。 1. 分区 分区是将一个大表分割为多个更小的子表,…...
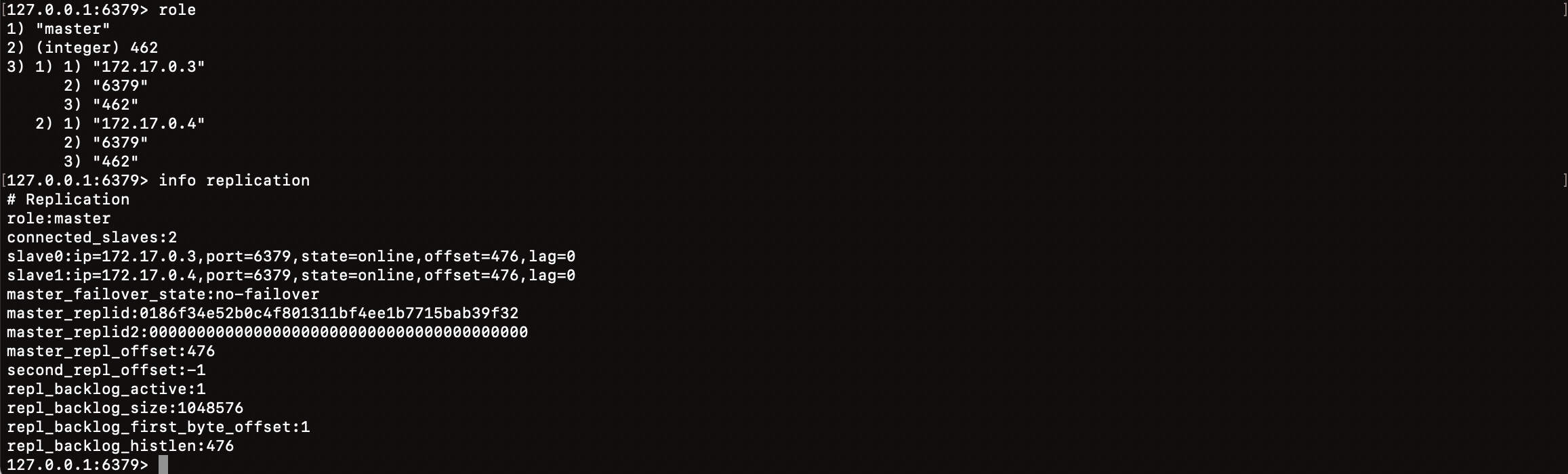
Redis主从复制集群的介绍及搭建
在现代的软件开发中,数据的可靠性和可用性是至关重要的。Redis,作为一个开源的、内存中的数据结构存储系统,以其出色的性能和灵活的数据结构,赢得了开发者们的广泛喜爱。而 Redis 的主从复制功能,更是为我们提供了一种…...

MAC M1芯片安装mounty读写移动硬盘中的文件
因为移动硬盘中的文件是微软公司NTFS格式,MAC只支持自己的APFS或者HFS,与微软的NTFS不兼容,所以需要第三方的软件来支持读写硬盘中的文件,经过一上午的折腾,最终选择安装mounty这个免费的第三方软件 工具网址连接&am…...

原生Js Canvas去除视频绿幕背景
Js去除视频背景 注: 这里的去除视频背景并不是对视频文件进行操作去除背景 如果需要对视频扣除背景并导出可以使用ffmpeg等库,这里仅作播放用所以采用这种方法 由于uniapp中的canvas经过封装,且 uniapp 的 drawImage 无法绘制视频帧画面&…...
每天10个小知识点)
Vue知识系列(1)每天10个小知识点
目录 系列文章目录知识点**1. Vue修饰符**的概念、作用、原理、特性、优点、缺点、区别、使用场景**2. 双向数据绑定**的概念、作用、原理、特性、优点、缺点、区别、使用场景**3. MVVM、MVC、MVP** 的概念、作用、原理、特性、优点、缺点、区别、使用场景**4. slot** 的概念、…...
聚合基本使用)
Elasticsearch(三)聚合基本使用
基础概念 bucket 数据分组,一些数据按照某个字段进行bucket划分,这个字段值相同的数据放到一个bucket中。可以理解成Java中的Map<String, List>结构,类似于Mysql中的group by后的查询结果。 metric: 对一个数据分组执行…...

单片机C语言实例:14、音频输出
一、喇叭发声原理 程序实例1: #include<reg52.h> //包含头文件,一般情况不需要改动,头文件包含特殊功能寄存器的定义sbit SPK P1^2; //定义喇叭端口 /*------------------------------------------------函数声明 --------------…...

docker 和 podman的区别
Podman 和 Docker 都是用于容器化应用程序的工具,它们在很多方面非常相似,但也有一些关键区别: 1. 架构和权限: - Docker:Docker 使用守护进程(dockerd)来管理容器,它需要在操作…...
苹果手机远程控制安卓手机,为什么不能发起控制?
这位用户想要用iOS设备远程控制安卓设备,在被控端安装好AirDroid之后,就在控制端的苹果手机上也安装了AirDroid,然而打开控制端的软件,却没有在手机界面上看到【远程控制】按钮,于是提出了以上疑问。 解答 想要让iOS设…...

Gradle 配置国内镜像
我们在使用gradle构建项目的时候,每当需要build或者刷新依赖的时候,由于gradle需要从服务器下载各种依赖包,速度非常慢,根本原因是由于gradle服务器在国外,而国内有些一些大厂和高校(比如阿里,华为…...

Spring AOP使用指南: 强大的面向切面编程技术
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

Spring Boot集成Elasticsearch实战
文章目录 一、简介二、安装与配置Elasticsearch三、集成Spring Boot与Elasticsearch1. 添加依赖与配置文件2. 创建Elasticsearch数据模型3. 定义Elasticsearch仓库接口4. 实现Elasticsearch数据操作 四、基本查询与索引操作1. 插入与更新数据2. 删除数据与索引3. 条件查询与分页…...

【python零基础入门学习】python基础篇之文件对象open、模块以及函数的使用(三)
本站以分享各种运维经验和运维所需要的技能为主 《python》:python零基础入门学习 《shell》:shell学习 《terraform》持续更新中:terraform_Aws学习零基础入门到最佳实战 《k8》暂未更新 《docker学习》暂未更新 《ceph学习》ceph日常问题解…...
【JavaEE】_CSS常用属性值
目录 1. 字体属性 1.1 设置字体家族 font-family 1.2 设置字体大小 font-size 1.3 设置字体粗细 font-weight 1.4 设置字体倾斜 font-style 2. 文本属性 2.1 设置文本颜色 color 2.2 文本对齐 text-align 2.3 文本装饰 text-decoration 2.4 文本缩进 text-indent 2.…...
vue组件库开发,webpack打包,发布npm
做一个像elment-ui一样的vue组件库 那多好啊!这是我前几年就想做的 但webpack真的太难用,也许是我功力不够 今天看到一个视频,早上6-13点,终于实现了,呜呜 感谢视频的分享-来龙去脉-大家可以看这个视频:htt…...
Java中快速排序的优化技巧:随机取样、三数取中和插入排序
目录 快速排序基础 优化1:随机取样 优化2:三数取中 优化3:插入排序 总结: 快速排序(Quick Sort)是一种高效的排序算法,它的平均时间复杂度为O(n log n)。然而,在某些情况下&…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
