数据结构和算法(4):栈与队列
栈 ADT 及实现
栈(stack)是存放数据对象的一种特殊容器,其中的数据元素按线性的逻辑次序排列,故也可定义首、末元素。
尽管栈结构也支持对象的插入和删除操作,但其操作的范围仅限于栈的某一特定端。
也就是说,若约定新的元素只能从某一端插入其中,则反过来也只能从这一端删除已有的元素。禁止操作的另一端,称作盲端。
后进先出:从栈结构的整个生命期来看,更晚(早)出栈的元素,应为更早(晚)入栈者。
| ADT | 功能 |
|---|---|
size() | 返回栈的规模 |
empty() | 判断栈是否为空 |
push(e) | 将 e 插至栈顶 |
pop() | 删除栈顶对象 |
top() | 引用栈顶对象 |
实现:
#include "../Vector/Vector.h" //以向量为基类,派生出栈模板类
template <typename T> class Stack: public Vector<T> { //将向量首/末端作为栈底/顶
public: //size()、empty()以及其它开放接口,均可直接沿用void push ( T const& e ) { insert ( size(), e ); } //入栈:等效于将新元素作为向量末元素插入T pop() { return remove ( size() - 1 ); } //出栈:等效于删除向量末元素T& top() { return ( *this ) [size() - 1]; } //取顶:直接返向量末元素
};
栈与递归
在 Windows 等 大部分操作系统中,每个运行中的二进制程序都配有一个调用栈(call stack)或执行栈(execution stack)。
借助调用栈可以跟踪属于同一程序的所有函数,记录它们之间的相互调用关系,并保证在每一调用实例执行完毕之后,可以准确地返回。
调用栈的基本单位是帧(frame)。
每次函数调用时,都会相应地创建一帧,记录该函数实例在二进制程序中的返回地址,以及局部变量、传入参数等,并将该帧压入调用栈。若在该函数返回之前又发生新的调用,则同样地要将与新函数对应的一帧压入栈中,成为新的栈顶。函数一旦运行完毕,对应的帧随即弹出,运行控制权将被交还给该函数的上层调用函数,并按照该帧中记录的返回地址确定在二进制程序中继续执行的位置。
在任一时刻,调用栈中的各帧,依次对应于那些尚未返回的调用实例,亦即当时的活跃函数实例。特别地,位于栈底的那帧必然对应于入口主函数main(),若它从调用栈中弹出,则意味着整个程序的运行结束,此后控制权将交还给操作系统.
进制转换
进制算法流程:
十进制转二进制: 使用除2取余法,从十进制数中反复除以2,将余数记录下来,然后将余数从下到上排列起来。
二进制转十进制: 从二进制的最右边开始,每个位上的数字乘以2的幂,然后将结果相加。
void convert ( Stack<char>& S,_int64 n, int base ) { //十进制数n到base进制的转换(迭代版)static char digit[] //0 <n, 1 < base <m 16,新进制下的数位符号,可视base取值范围适当扩充= { '0', '1', '2','3', '4' , '5', '6','7','8', '9','A','B','C','D','E','F');while ( n > e ) { //由低到高,逐一计算出新进制下的各数位int remainder = ( int ) ( n % base ); S.push(digit[remainder] ); //余数(当前位)入栈n/= base; //n 更新为其对 base 的除商}
}//新进制下由高到低的各数位,自顶而下保存于栈s中main(){Stack<char> S; convert(S, n, base); //用栈记录转换得到的各数位while(!S.empty())printf("%c",S.pop()); //逆序输出
}
括号匹配
括号匹配的任务是,对任一程序块,判断其中的括号是否在嵌套的意义下完全匹配(简称匹配)。
顺序扫描表达式,用栈记录已扫描的部分:凡遇 (,则进栈;凡遇 ),则出栈。
#include <iostream>
#include <stack>
#include <string>bool isBracketMatch(const std::string& input) {std::stack<char> brackets;for (char c : input) {if (c == '(' || c == '{' || c == '[') {brackets.push(c);} else if (c == ')' || c == '}' || c == ']') {if (brackets.empty()) {return false; // 括号不匹配,没有左括号与右括号匹配}char top = brackets.top();brackets.pop();if ((c == ')' && top != '(') || (c == '}' && top != '{') || (c == ']' && top != '[')) {return false; // 括号不匹配}}}return brackets.empty(); // 所有括号都正确匹配
}int main() {std::string input = "{[()]}";if (isBracketMatch(input)) {std::cout << "Brackets are matched." << std::endl;} else {std::cout << "Brackets are not matched." << std::endl;}return 0;
}在只有一种括号类型时,可以使用计数器起到与栈相同的效果;但存在多种括号类型时,计数器无法使用。
栈混洗
栈混洗是一个经典的问题,涉及到两个栈,其中一个栈包含一组数字,需要确定是否可以通过一系列栈操作将这些数字从一个初始顺序重新排列成另一个目标顺序。
问题的形式如下:
给定两个整数数组,一个代表初始栈的顺序,另一个代表目标栈的顺序,判断是否可以通过以下栈操作将初始栈的元素重新排列成目标栈的顺序:
1.将元素从初始栈的顶部移动到输出栈(可以看作是出栈操作)。
2.将元素从输入栈的底部移动到输出栈(可以看作是将输入栈反转后的出栈操作)。
如果可以,返回 true,否则返回 false。
解决这个问题的一种常见方法是使用模拟。可以创建一个辅助栈来模拟操作,并按照目标顺序进行操作。具体步骤如下:
1.初始化一个辅助栈。
2.遍历目标栈的顺序(从左到右):
3.如果目标栈的当前元素与初始栈的顶部元素相同,直接从初始栈弹出元素。
4.否则,从初始栈中弹出元素,并将其推入辅助栈,直到找到与目标栈当前元素相同的元素。
5.继续遍历目标栈,如果辅助栈的栈顶元素与目标栈的当前元素相同,则从辅助栈中弹出元素。
6.最后,如果初始栈为空并且辅助栈也为空,返回 true;否则返回 false。
#include <iostream>
#include <stack>
#include <vector>bool isStackPermutation(const std::vector<int>& input, const std::vector<int>& target) {std::stack<int> initialStack;std::stack<int> auxStack;for (int num : input) {initialStack.push(num);}for (int num : target) {while (!initialStack.empty() && initialStack.top() != num) {auxStack.push(initialStack.top());initialStack.pop();}if (!initialStack.empty() && initialStack.top() == num) {initialStack.pop();} else if (!auxStack.empty() && auxStack.top() == num) {auxStack.pop();} else {return false;}}return initialStack.empty() && auxStack.empty();
}int main() {std::vector<int> input = {1, 2, 3};std::vector<int> target = {2, 1, 3};if (isStackPermutation(input, target)) {std::cout << "The permutation is valid." << std::endl;} else {std::cout << "The permutation is not valid." << std::endl;}return 0;
}
栈混洗计数为: ( 2 n ! ) ( n + 1 ) ! n ! = c a t a l a n ( n ) \frac{(2n!)}{(n+1)!n!} = catalan(n) (n+1)!n!(2n!)=catalan(n)
甄别栈混洗: B B B 是 A A A 的一个栈混洗,当且仅当对于任意 1 ≤ i < j < k ≤ n 1 \leq i < j < k \leq n 1≤i<j<k≤n,P 中都不包含如下模式: { . . . , k , . . . , i , . . . , j , . . . } \{ ..., k, ..., i, ..., j, ...\} {...,k,...,i,...,j,...},例如{3,1,2}.
中缀表达式求值
思路:
将中缀表达式转换为后缀表达式:创建一个空栈,用于存储操作符。从左到右遍历中缀表达式中的每个字符(数字和操作符)。如果遇到数字,直接输出到输出队列。如果遇到操作符:如果栈为空,将操作符压入栈。否则,比较操作符与栈顶操作符的优先级:如果操作符优先级高于栈顶操作符,将操作符压入栈。否则,弹出栈中较高或相等优先级的操作符,并将它们输出到输出队列,直到遇到更低优先级的操作符或栈为空,然后将当前操作符压入栈。如果遇到左括号"(",将其压入栈。如果遇到右括号")",弹出栈中的操作符并将它们输出到输出队列,直到遇到左括号"(",然后将左括号从栈中弹出但不输出。遍历结束后,将栈中剩余的操作符全部输出到输出队列。计算后缀表达式的值:创建一个空栈,用于存储操作数。从左到右遍历后缀表达式中的每个元素(数字和操作符)。如果遇到数字,将其压入栈。如果遇到操作符,从栈中弹出所需数量的操作数(通常是两个),执行相应的运算,然后将结果压入栈。最终,栈中将只剩下一个元素,即表达式的值。
代码实现:
#include <iostream>
#include <stack>
#include <string>
#include <sstream>
#include <cctype>//返回操作符的优先级,优先级越高,越早进行计算
int precedence(char op) {if (op == '+' || op == '-') return 1;if (op == '*' || op == '/') return 2;return 0;
}
//于执行操作符的运算,根据不同的操作符执行不同的操作,并返回结果
double applyOperator(double operand1, double operand2, char op) {switch (op) {case '+': return operand1 + operand2;case '-': return operand1 - operand2;case '*': return operand1 * operand2;case '/': return operand1 / operand2;default: return 0.0; // 处理未知操作符}
}double evaluateInfixExpression(const std::string& expression) {std::stack<char> operators;std::stack<double> operands;//operators 用于存储操作符,operands 用于存储操作数std::istringstream iss(expression);//创建了一个 std::istringstream 对象,将中缀表达式字符串 expression 包装为输入流,并准备逐个读取字符串中的标记std::string token;while (iss >> token) { //程序检查当前标记 token 是数字还是括号。如果是数字(包括正数和负数),将其转换为 double 类型并压入 operands 栈。如果是左括号 "(",将其压入 operators 栈。if (isdigit(token[0]) || (token.length() > 1 && token[0] == '-' && isdigit(token[1]))) {double operand = std::stod(token);operands.push(operand);}else if (token == "(") {operators.push('(');}else if (token == ")") {//在遇到右括号 ")" 时,程序将执行一系列操作来处理括号内的表达式。它会弹出操作符直到遇到左括号 "(",并对括号内的表达式进行计算,将结果压入 operands 栈。//如果在遇到左括号之前就遇到了栈空或其他操作符,表示右括号没有正确匹配,将返回0.0表示错误。while (!operators.empty() && operators.top() != '(') {char op = operators.top();operators.pop();if (operands.size() < 2) {// 处理错误:操作数不足return 0.0;}double operand2 = operands.top();operands.pop();double operand1 = operands.top();operands.pop();double result = applyOperator(operand1, operand2, op);operands.push(result);}if (!operators.empty() && operators.top() == '(') {operators.pop();}else {// 处理错误:未匹配的右括号return 0.0;}}else {while (!operators.empty() && precedence(operators.top()) >= precedence(token[0])) {char op = operators.top();operators.pop();if (operands.size() < 2) {// 处理错误:操作数不足return 0.0;}double operand2 = operands.top();operands.pop();double operand1 = operands.top();operands.pop();double result = applyOperator(operand1, operand2, op);operands.push(result);}operators.push(token[0]);}}while (!operators.empty()) {char op = operators.top();operators.pop();if (operands.size() < 2) {// 处理错误:操作数不足return 0.0;}double operand2 = operands.top();operands.pop();double operand1 = operands.top();operands.pop();double result = applyOperator(operand1, operand2, op);operands.push(result);}if (operands.size() != 1 || !operators.empty()) {// 处理错误:操作数和操作符未匹配return 0.0;}return operands.top();
}int main() {std::string infixExpression = "2 + 3 * 4 - 1";double result = evaluateInfixExpression(infixExpression);if (result != 0.0) {std::cout << "Result: " << result << std::endl;}else {std::cout << "Invalid expression." << std::endl;}return 0;
}
当前的操作符比栈顶的操作符优先级低时,进行实际的运算。
逆波兰表达式
逆波兰表达式(Reverse Polish Notation,RPN),也称为后缀表达式,是一种数学表达式表示法,其中操作符在操作数之后。这种表示法消除了括号,并且使得表达式的计算顺序更加明确,不需要考虑操作符的优先级。
手工转换
假设:事先未就运算符之间的优先级关系做出过任何约定
1)用括号显式地表示优先级
2)将运算符移到对应的右括号后
3)抹去所有括号,整理。
//原式
( 0 ! + 1 ) * 2 ^ ( 3 ! + 4 ) - ( 5 ! - 67 - ( 8 + 9 ) )
//增添足够多的括号
( ( ( ( 0 ) ! + 1 ) * ( 2 ^ ( ( 3 ) ! + 4 ) ) ) - ( ( ( 5 ) ! - 67 ) - ( 8 + 9 ) ) )
//各运算符后移,使之紧邻于其对应的右括号的右侧:
( ( ( ( 0 ) ! 1 ) + ( 2 ( ( 3 ) ! 4 ) + ) ^ ) * ( ( ( 5 ) ! 67 ) - ( 8 9 ) + ) - ) -
//最后抹去所有括号:
0 ! 1 + 2 3 ! 4 + ^ * 5 ! 67 - 8 9 + - -
操作数之间的相对次序,在转换前后保持不变;而运算符在RPN中所处的位置,恰好就是其对应的操作数均已就绪且该运算可以执行的位置。
队列 ADT 及实现
队列像栈一样,也是受限的序列:
只能在队尾插入(查询):enqueue() + rear()
只能在队头删除(查询):dequeue() + front()
先进先出,后进后出。
队列既然属于序列的特列,故亦可直接基于向量或列表派生。
相关文章:
:栈与队列)
数据结构和算法(4):栈与队列
栈 ADT 及实现 栈(stack)是存放数据对象的一种特殊容器,其中的数据元素按线性的逻辑次序排列,故也可定义首、末元素。 尽管栈结构也支持对象的插入和删除操作,但其操作的范围仅限于栈的某一特定端。 也就是说…...
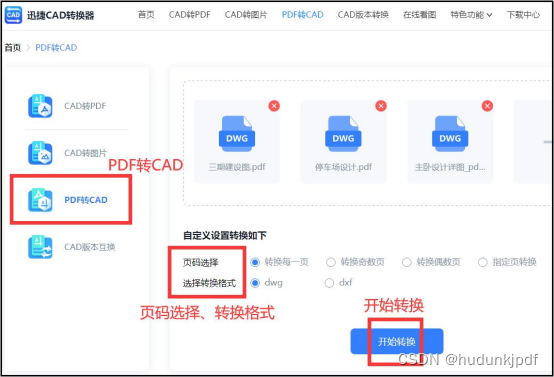
pdf怎么转换成dwg格式?简单转换方法分享
当我们需要在CAD中编辑PDF文件中的向量图形时,将PDF转换成DWG格式是一个非常好的选择。因为PDF是一种非常流行的文档格式,很多时候我们会接收到PDF文件,但是PDF文件中的向量图形无法直接在CAD中编辑。而将PDF转换成DWG格式后,就可…...
uniapp使用H5实现预览pdf文件
下载后把压缩包解压到自己的项目的static文件夹下的pdf文件下,如图 新建一个文件名为filePreview.vue <template><view><web-view :src"allUrl"></web-view></view> </template><script>export default {dat…...

Studio 3T for MongoDB的介绍及语法简单介绍
用法介绍 Studio 3T是一款用于MongoDB数据库管理和开发的图形化工具,它提供了许多功能来简化MongoDB的操作和开发过程。以下是一些常见的Studio 3T用法: 连接到MongoDB服务器: 打开Studio 3T并创建一个新连接配置。输入MongoDB服务器的主机名…...
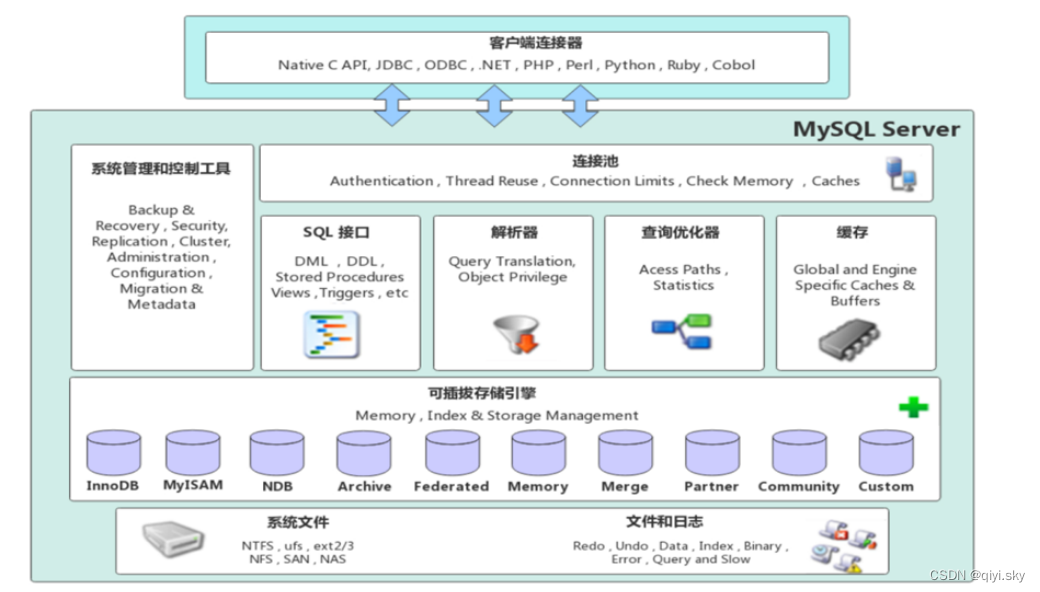
MySQL数据库——存储引擎(1)-MySQL体系结构、存储引擎简介
目录 MySQL体系结构 连接层 服务层 引擎层 存储层 存储引擎简介 概念 语句 演示 下面开始学习进阶篇的第一个内容——存储引擎 分为四点学习: MySQL体系结构存储引擎简介存储引擎特点存储引擎选择 MySQL体系结构 连接层 最上层是一些客户端和链接服务&am…...

211. 添加与搜索单词 - 数据结构设计
211. 添加与搜索单词 - 数据结构设计 class WordDictionary { public:struct Node{Node *node[26];bool is_end;Node(){is_endfalse;for(int i0;i< 26;i){node[i]NULL;}}};Node *root;WordDictionary() {root new Node();}void addWord(string word) {auto p root;for(aut…...
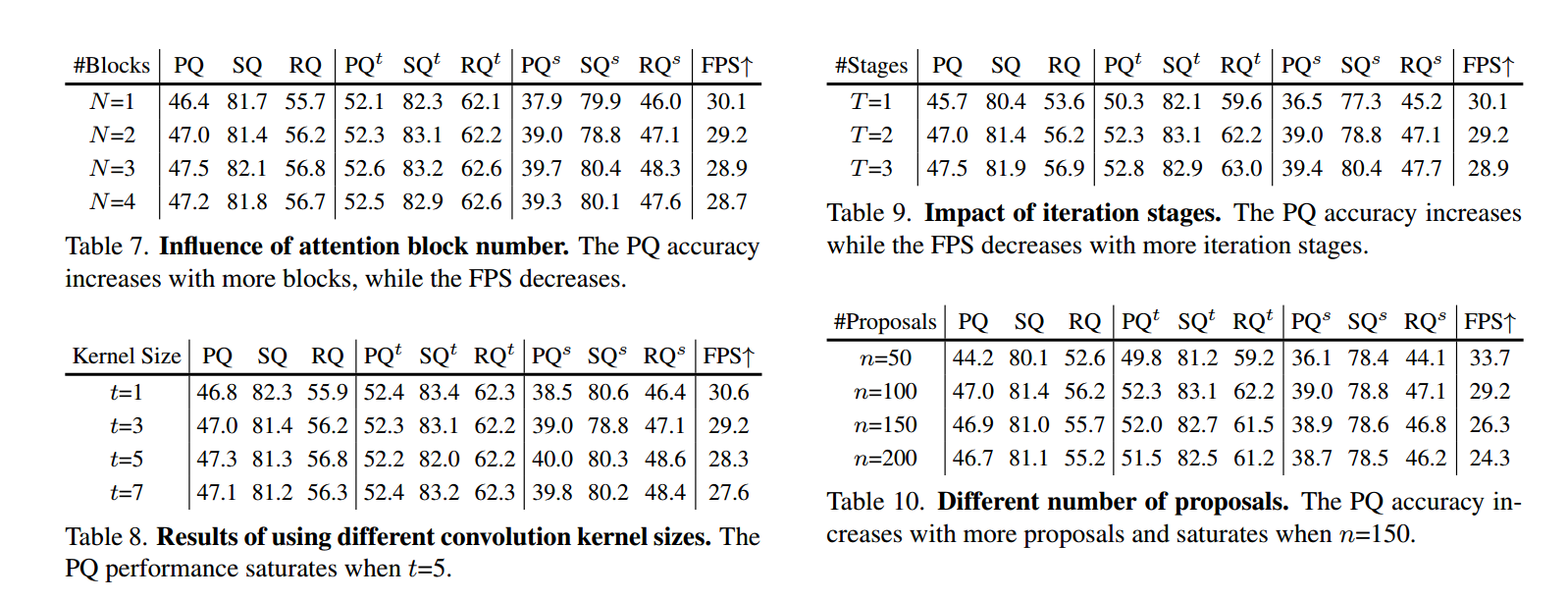
【深度学习】You Only Segment Once: Towards Real-Time Panoptic Segmentation,YOSO全景分割
论文:https://arxiv.org/abs/2303.14651 代码:https://github.com/hujiecpp/YOSO 文章目录 Abstract1. Introduction2. Related Work3. Method3.1. Task Formulation3.2. Feature Pyramid Aggregator3.3. Separable Dynamic Decoder 4. Experiments4.1. …...
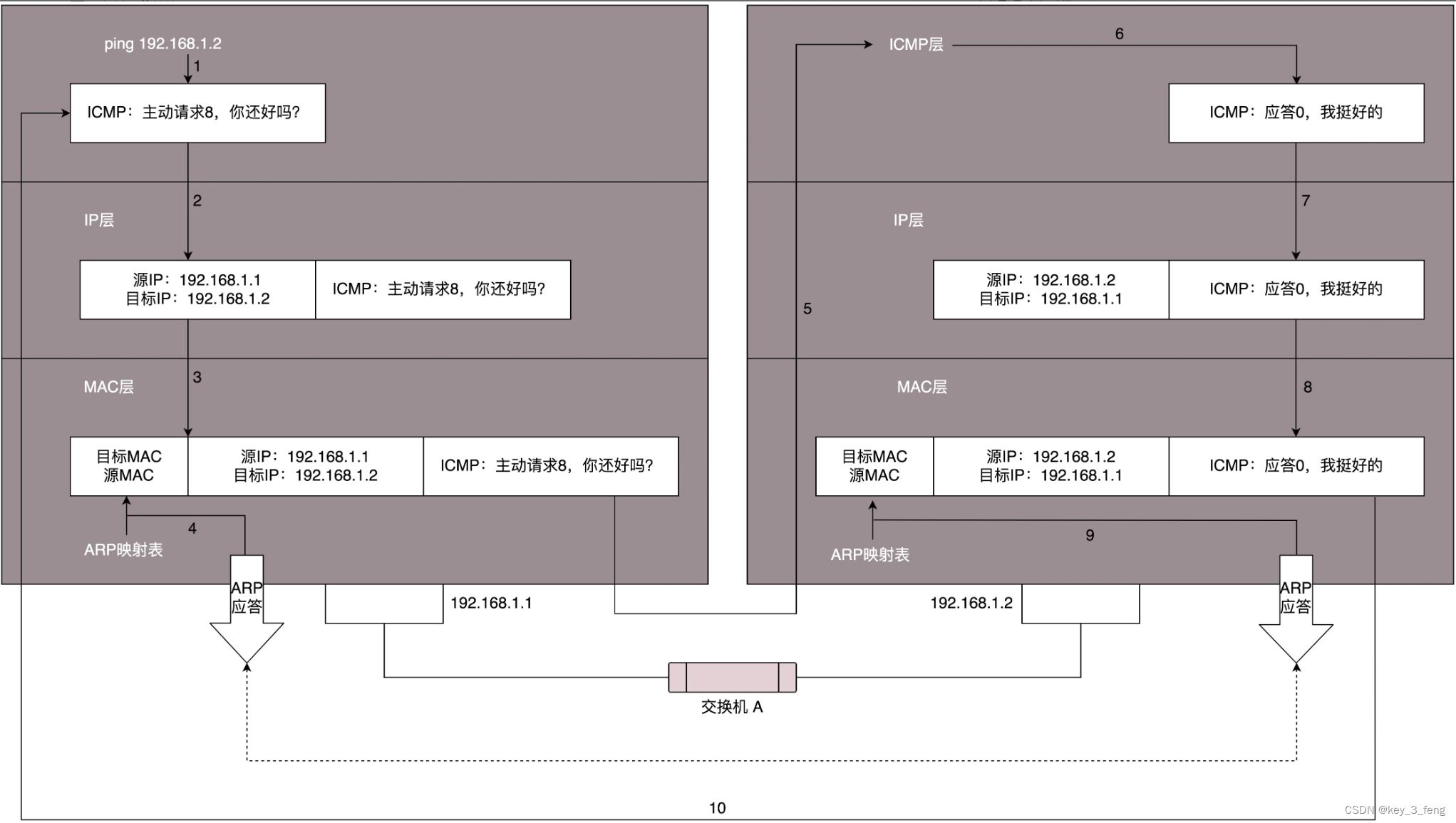
ping与Traceroute是如何工作的
ping 是基于 ICMP 协议工作的。ICMP 全称 Internet Control Message Protocol,就是互联网控制报文协议。 ICMP 报文是封装在 IP 包里面的。因为传输指令的时候,肯定需要源地址和目标地址。它本身非常简单。 ICMP 报文有很多的类型,不同的类型…...

CentOS Python环境搭建
安装依赖 yum install -y libffi-devel wget gcc make zlib-devel openssl openssl-devel ncurses-devel openldap-devel gettext bzip2-devel xz-devel下载安装包 wget "https://www.python.org/ftp/python/3.9.10/Python-3.9.10.tar.xz" 编译安装 # 3.1、解压安装包…...
亚马逊云科技与伊克罗德推出AI绘画解决方案——imAgine
在过去的数月中,亚马逊云科技已经推出了多篇介绍如何在亚马逊云科技上部署Stable Diffusion,或是如何结合Amazon SageMaker与Stable Diffusion进行模型训练和推理任务的内容。 为了帮助客户快速、安全地在亚马逊云科技上构建、部署和管理应用程序&#x…...

机器学习课后习题 --- 逻辑回归
(一)单选题 1.一监狱人脸识别准入系统用来识别待进入人员的身份,此系统一共包括识别4种不同的人员:狱警,小偷,送餐员,其他。下面哪种学习方法最适合此种应用需求: A:二分类问题 …...
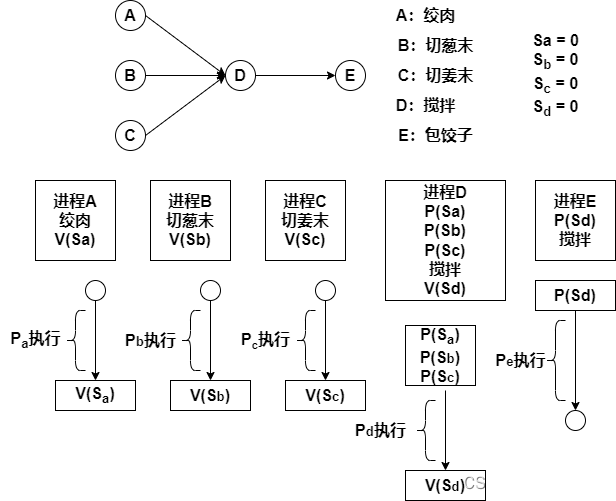
软件设计师学习笔记9-进程调度
目录 1. PV操作 1.1进程的同步与互斥 1.1.1互斥 1.1.2同步 1.2 PV操作 1.2.1信号量 1.2.2 PV操作的概念 2.信号量与PV操作 2.1 PV操作与互斥模型 2.2 PV操作与同步模型 2.3 互斥与同步模型结合 3.前趋图与PV操作 1. PV操作 1.1进程的同步与互斥 1.1.1互斥 互斥&…...
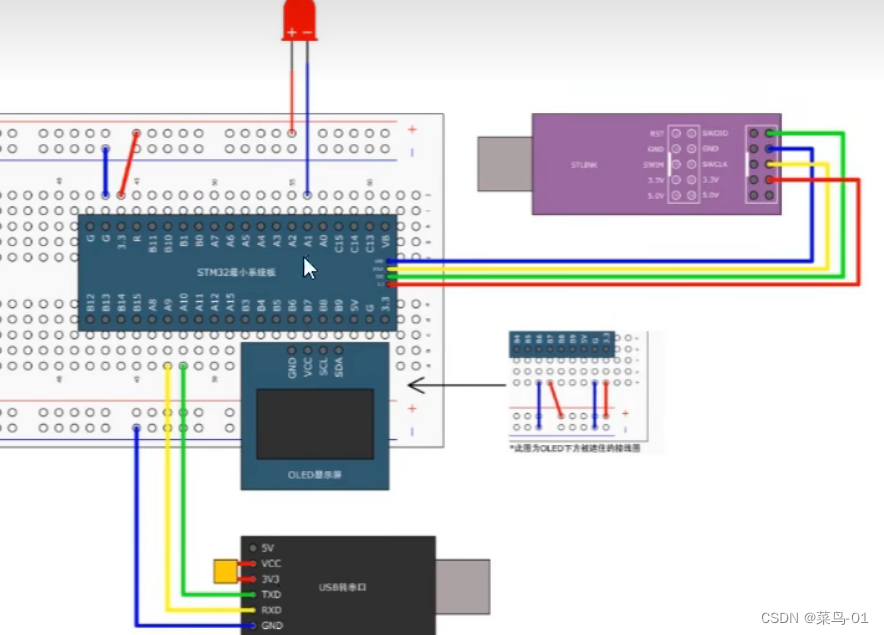
09:STM32-------USART串口通信+串口数据包
目录 一:串口协议 1:通信接口 2:串口通信 3:硬件电路 4:电平标准 5:串口参数及其时序 二:USART介绍 1:简历 2:USART框图 3:USART的基本结构 4:数据帧 5: 波特率发生器 6:数据模式 三:案例 A:串口发送--单发送 1:连接图 2:函数介绍 3:代码 B:串口发送接收 1…...

“安全即服务”为网络安全推开一道门
8月30日,三六零(下称“360”)集团发布了2023年半年报,其中安全业务第二季度收入6.54亿元,同比增长98.76%,环比增长157.16%,安全第二增长曲线已完全成型!特别值得一提的是,…...
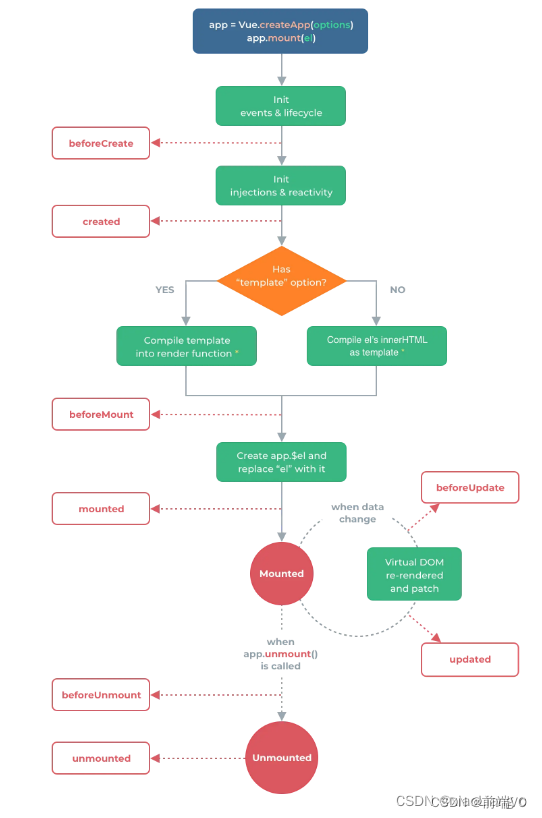
vue3的生命周期
1.vue3生命周期官方流程图 2.vue3中的选项式生命周期 vue3中的选项式生命周期钩子基本与vue2中的大体相同,它们都是定义在 vue实例的对象参数中的函数,它们在vue中实例的生命周期的不同阶段被调用。生命周期函数钩子会在我们的实例挂载,更新…...
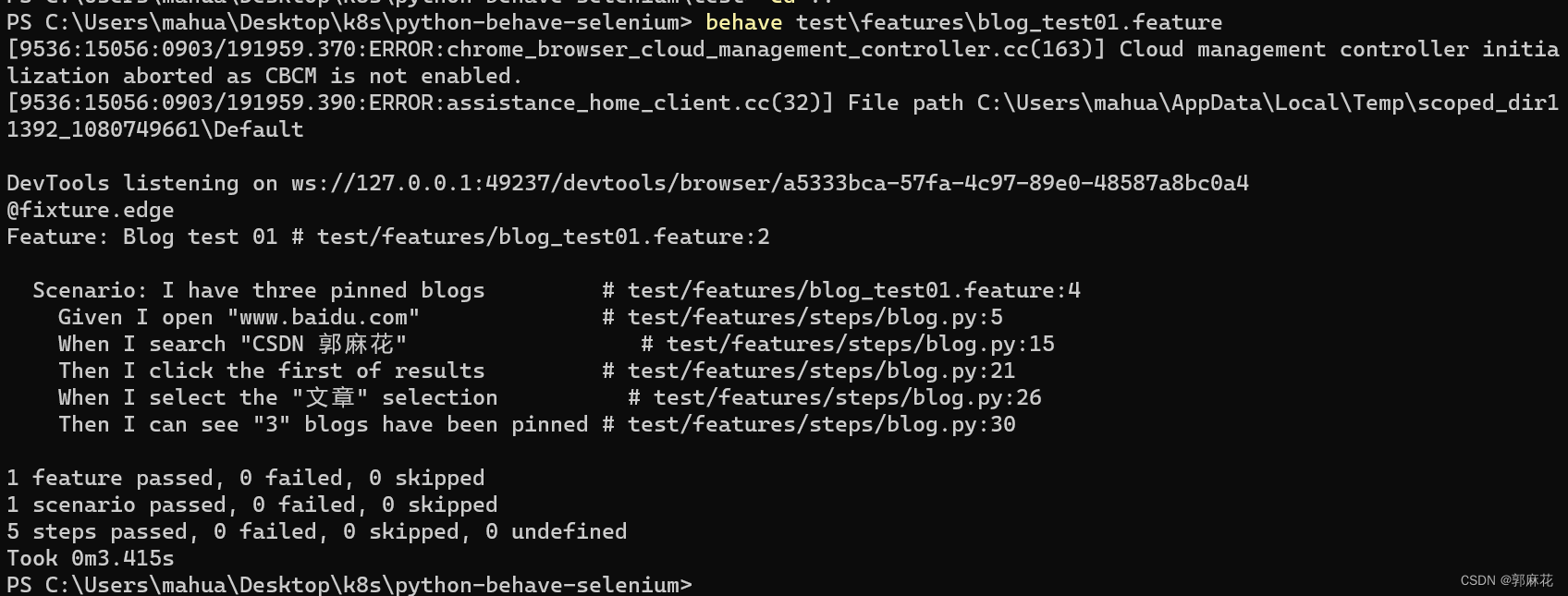
[E2E Test] Python Behave Selenium 一文学会自动化测试
前言 本文将使用Python Behave与Selenium,和同学们一起认识自动化测试,并附上完整的实践教程。 项目源码已上传:CSDN 郭麻花 Azure Repo python-behave-selenium 核心概念 1. 什么是E2E Test E2E即End-to-end,意思是从头到尾…...

Knowledge Graph Prompting for Multi-Document Question Answering
本文是LLM系列文章,针对《Knowledge Graph Prompting for Multi-Document Question Answering》的翻译。 多文档问答中的知识图谱提示 摘要1 引言2 符号3 知识图谱构建4 LM引导的图形遍历器5 实验6 相关工作7 结论 摘要 大型语言模型的“预训练、提示、预测”范式…...
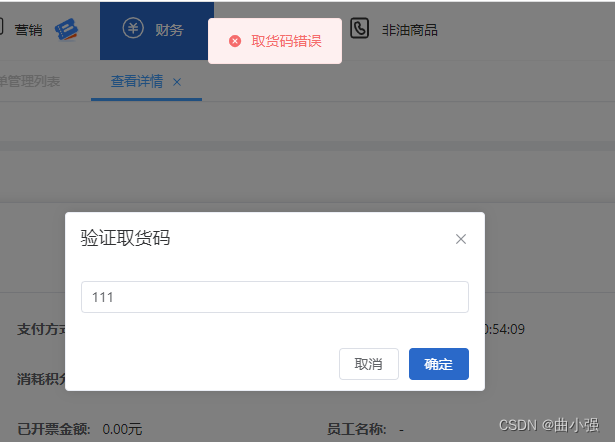
ElMessageBox.prompt 点击确认校验成功后关闭
ElMessageBox.prompt(, 验证取货码, {inputPattern: /^.{1,20}$/,inputErrorMessage: 请输入取货码,inputPlaceholder: 请输入取货码,beforeClose: (action, instance, done) > {if (action confirm) {if (instance.inputValue) {let flag false;if (flag) {done()} else …...
调整Windows11桌面图标间隔
调整Windows11桌面图标间隔 WinR 快捷键如何使用 在Windows系统中,通过 WinR 的快捷键可以快速打开Windows系统的“运行”窗口,然后在这里输入相应的命令就可以快速执行指定的任务。 具体的操作方法是,同时按下键盘上的Windows键和R键即可。…...

Spring最佳实践: 构建高效可维护的Java应用程序
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...

归并排序:分治思想的高效排序
目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法,由约翰冯诺伊曼在1945年提出。其核心思想包括: 分割(Divide):将待排序数组递归地分成两个子…...

【阅读笔记】MemOS: 大语言模型内存增强生成操作系统
核心速览 研究背景 研究问题:这篇文章要解决的问题是当前大型语言模型(LLMs)在处理内存方面的局限性。LLMs虽然在语言感知和生成方面表现出色,但缺乏统一的、结构化的内存架构。现有的方法如检索增强生成(RA…...
