AVL树 模拟实现(插入)
目录
模拟插入节点
左单旋
右单旋
右左双旋
左右双旋
总结
实现
插入实现
左单旋实现
右单旋实现
右左双旋实现
左右双旋实现
AVL树 模拟实现(插入)
AVL 树,是高度平衡二叉搜索树,其主要通过旋转来控制其左右子树的高度不超过1,这样就能达到搜索效率基本等同于满二叉树(O(LogN)),所以 AVL 并不会向普通的搜索树一样,在极端情况下退化为单枝。
首先AVL在平衡的前提下,还要保证其是一颗搜索树,所以在插入的时候还是按照搜索树的插入规则来。
AVL 树的高度就是右子树减左子树的高度。
AVL 树的实现有几种,其中一种是借用平衡因子来查看其是否平衡,如果不适用平衡因子,那么就需要使用高度查看是否平衡,但是加入平衡因子会跟简单一些,所以下面我们实现的AVL 树是借用平衡因子来维持平衡的。
模拟插入节点
如果是第一次插入,以及第二次插入那么和搜索树是一摸一样的,为什么呢?
因为如果是第一次插入,那么就是插入到根节点,所以该是是平衡的,无需做其他的操作来保持其平衡,而第二次插入也是不需要我们做其他操作的,同样是因为第二次插入也是平衡的(左右子树的高度不超过1)。
左单旋
插入两个节点如图所示:
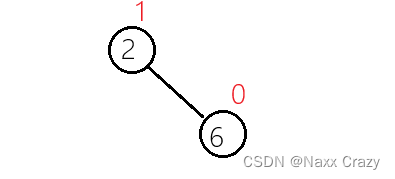
这时候,6 节点的高度就为 0,而 2 节点的高度为 1,因为 6 节点的左右子树的高度都为 0,而 2 节点的右子树的高度为 1,而左子树的高度为 0.
如果是两个节点的话,是无法达到完全平衡的,所以并不是AVL树不想达到完全平衡,而是只有在满二叉树的情况下才能达到完全平衡。
下面如果在插入一个节点,那么就会引发旋转:
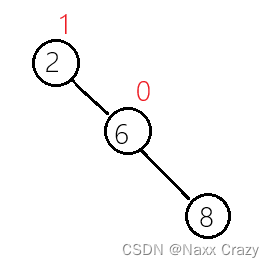
如果这时候插入节点 8,那么首先我们就能看到这棵树已经不平衡了,但是我们要怎么使用平衡因子来控制?
插入节点 8,此时节点 8 的平衡因子肯定是 0,那么现在 8 在节点 6 的右边,所以 6 要对它的平衡因子进行+1操作:
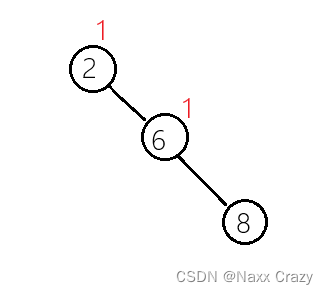
此时节点 6 的平衡因子变为了 1,现在我们想一下,如果平衡因子由 0 变为 1表示的是什么?
节点刚开始的平衡因子是 0 ,说明刚开始的时候该树是平衡的,变为 1说明该树的右子树多增加了一个节点的高度,所以说明该树的高度发生了变化,所以既然该节点的高度发生了变化,那么该节点的父亲节点的高度可能也会发生变化,所以这时候我们需要向上检查父亲节点的高度:

这时候父亲节点的高度变为了 2,说明此时已经不平衡了,那么要怎样旋转?
我们发现这样的不平衡是单纯的右边高,所以我们尽可能向左旋转,将高度压下去,也就是使用左单旋:
1. 我们需要将父亲节点(2),的右子树连接到,cur(6) 节点的左子树上
2. 我们将cur(6)节点的左子树,连接成父亲节点(2)
所以旋转结束后就是这样:
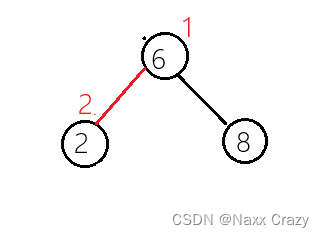
但是我们的平衡因子是不正确的,所以如果我们使用左单旋转,旋转之后我们需要将父亲节点(2),和cur节点(6)的平衡因子变为 0.
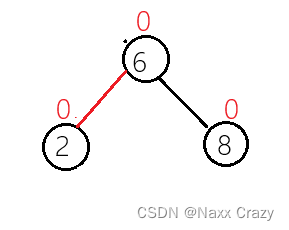
上面我们为什么要将cur 节点的左孩子给父亲节点呢?
因为这里我们只是画了一个节点,我们有可能右多个节点,所以我们还需要处理好其他节点,但是由于我们只是对cur 的左子树进行的调换位置,我们并未使其高度发生变化,所以我们也自然不需要对其的平衡因子进行调整:
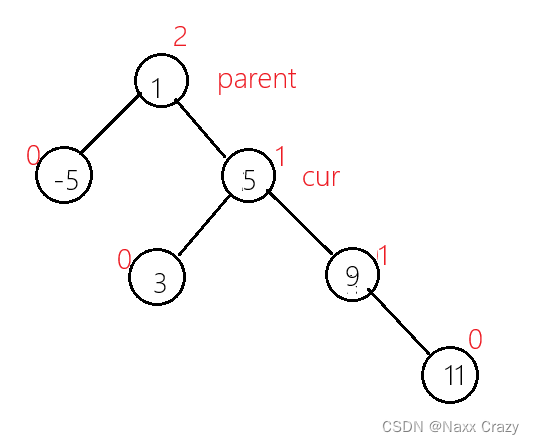
也就是像我们上图这样,cur节点,还有左子树:
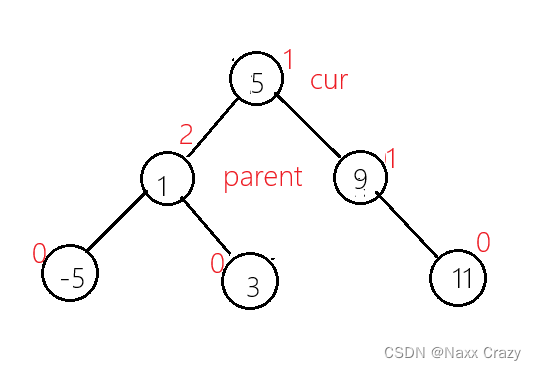
上图就是进行旋转之后的样子,然后进行修正平衡因子(parent 为 0,cur 为 0:
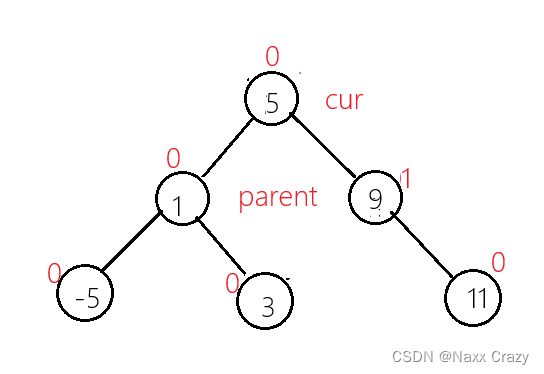
右单旋
如果我们的方向不同呢?也就是整个树是单纯的左边高:
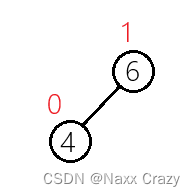
插入节点:
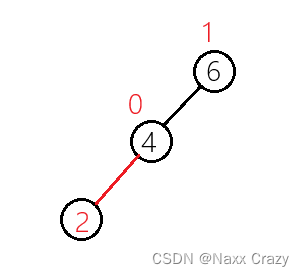
修正平衡因子:
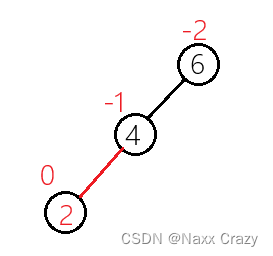
这里我们发现节点 6 已经不平衡了,需要旋转来维持平衡,这时候我们发现它是单纯的左边高,也就是我们需要像右旋转,也就是右单旋:
1. 将节点 4 的右子树连接到节点 6 的左子树上
2. 将节点 6 连接到节点 4 的右子树上
旋转结束后就就是这样:
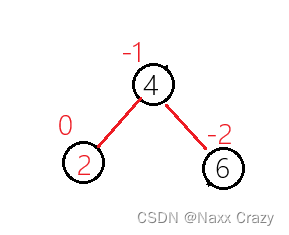
我们还是将parent节点(6)和 cur节点(4)的平衡因子修改为 0.
而这里处理cur节点的右子树的原因和处理左单旋时候的 cur 的左子树是一样的原因。
经过上面的左单旋和右单旋,我们发现:
1. 如果插入节点到当前节点的左子树:那么就让当前节点的平衡因子进行 ‘减减’ 操作
2. 如果插入节点到当前节点的右子树:那么就让当前节点的平衡因子进行 ‘加加’ 操作
3.如果平衡因子由 0 变为 1 或者由 0 变为 -1 ,那么就说明当前节点的左右子树的高度发生的变化,需要对当前节点的父亲节点进行平衡因子的跟新。
4.如果当前节点的平衡因子被跟新为 2 或者 -2 ,那么说明当前节点的左右子树已经不平衡了,需要旋转来调节平衡。
5. 什么时候插入结束?
1)当插入的节点是根节点,那么插入后就可以结束了。
2)插入的节点已经存在
3)插入成功并且修正平衡因子后,父亲的平衡因子变为 0 ,变为 0 说明父亲之前的平衡因子不为 0,而变为 0 说明父亲的高度没有发生变化,所以无需在向上调整,插入也就结束。
4)修正平衡因子后,发现某一节点需要旋转,而旋转并且修正平衡因子后,插入结束。
上面说的修正平衡因子是一个循环的过程,因为在修正平衡因子的时候,可能将父亲的平衡因子由0 变为 1 或者 -1 ,说明父亲的高度变化了,所以此时就需要将父亲给给 cur 然后继续向上调整,还有一个插入结束的调节,就是父亲为空也插入结束了,父亲为空说明为根节点。
6. 判断是左单旋还是右单旋:
1)如果是单纯的左边高,那么就进行右单旋,那么怎么判断是单纯的左边高?单纯的左边高,就是父亲节点的平衡因子为 -2 ,而 cur 节点的平衡因子为 -1.
2)如果是单纯的右边高,那么就进行右单旋,右单旋的特征是,parent 的平衡因子是 2, cur 的平衡因子是 1
右左双旋
上面我们插入后总是一边高,但是我们还是右其他的情况,也就是下面这种:
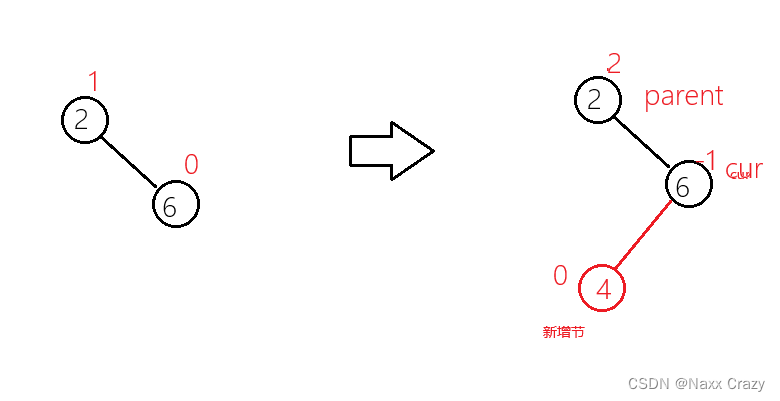
我们这种该怎么样旋转呢?我们可以先试一下左单旋,因为这里我们发现是右边高:
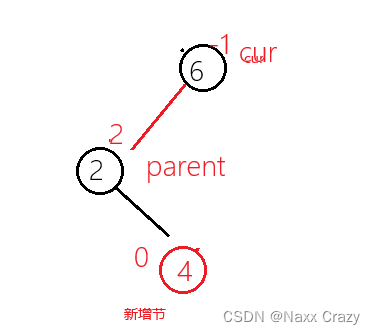
在旋转后,我们发现高度并没有被压缩,而是调了个个,所以如果是这种情况的话,单纯的左或者右是不能完成任务的,而是需要使用双旋。
我们可以先对cur 节点进行右单旋:
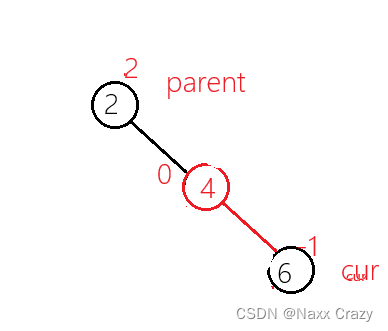
经过我们前面对 cur 节点进行的右单旋,我们此时已经变为一边高了,所以此时我们在对 parent 节点进行左单旋就可以完成压缩高度任务:
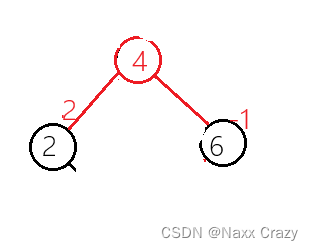
我们此时经过旋转后的 parent 和 cur 节点的平衡因子变为 0了:
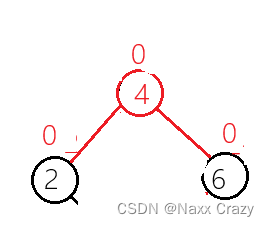
但是这只是我们节点 4 就是新插入的节点,那么假设是其他情况呢?
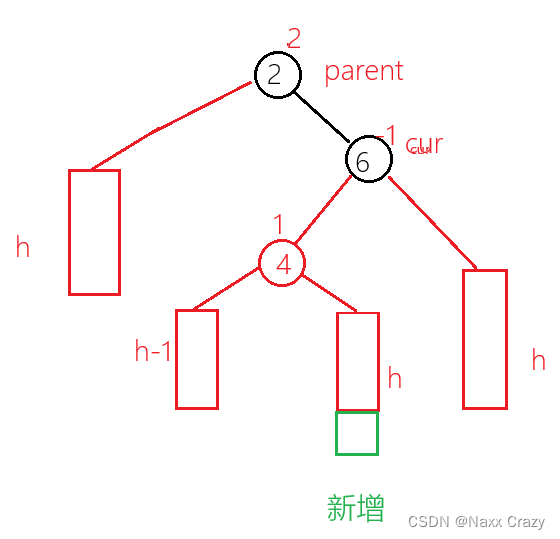
上图是抽象图,可以表示该种情况下所有可能的情况,如果当 h == 0 的时候,就表示的是 4 节点是新增,但是无论 h 是多少,我们都可以使用右左双旋。
首先对该树的cur 节点使用右单旋:
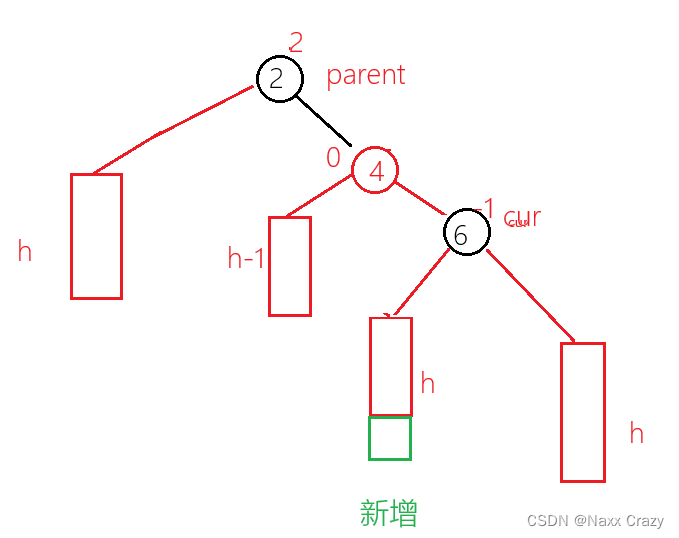
旋转后就变为了这样,也就是单纯的右边高,所以我们在使用左单旋对parent节点:
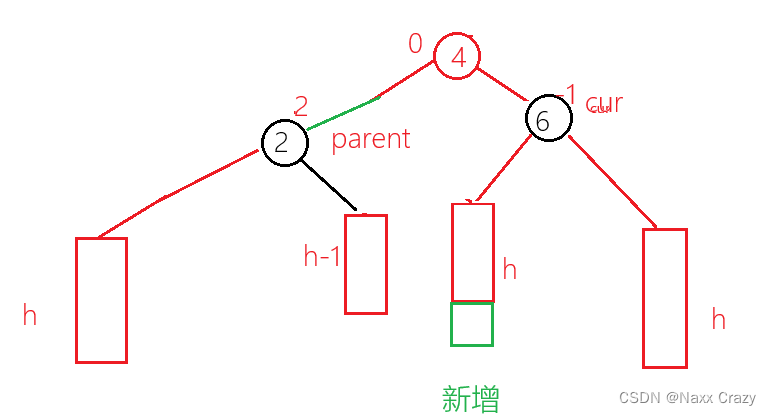
但是这时候 parent 和 cur 节点的平衡因子都是 0,那么我们要怎么调节平衡因子呢?对于这种情况来说,我们是将parent 的平衡因子调整为 -1 ,cur 的平衡因子为 0,即可,但是我们要是插入的位置不是刚开始插入的位置呢?
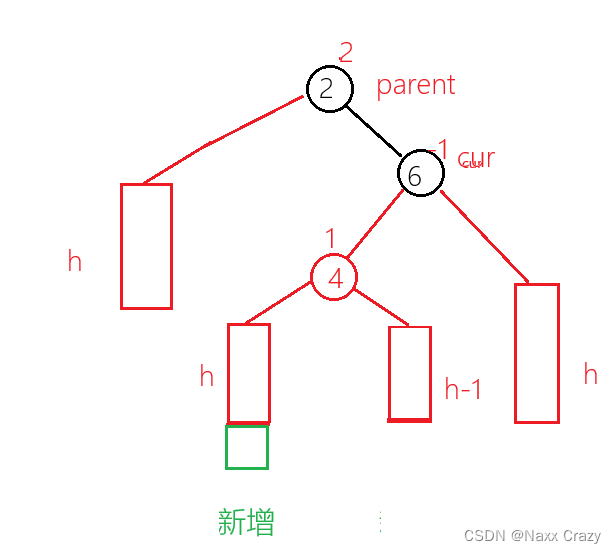
如果插入到该位置,那么金国旋转后的结果是这样的:
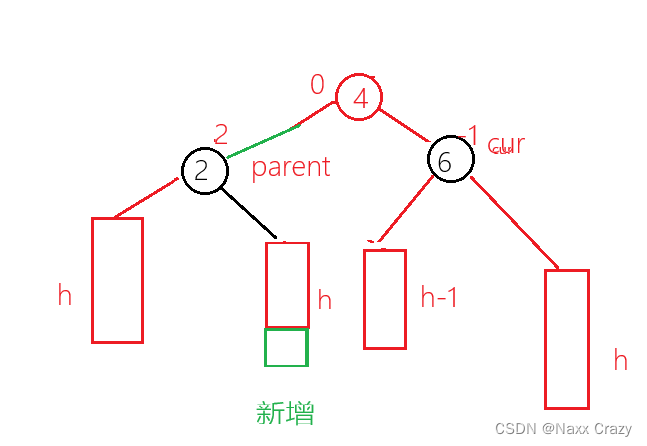
所以此时跟新平衡因子应该是 parent 为 0 ,cur 的平衡因子应该为 1,所以我们插入位置不同的话,我们的平衡因子的跟新策略是不同的,所以我们还要记录插入位置的平衡因子。
我们为了更好的描述,我们将节点 4 称为 curLeft。
我们发现我们在旋转结束后,curLeft 的左右子树被parent 和 cur 代替,而他自己的左子树被分给了parent 的 right 子树 ,而它的右子树被分给了cur 的 left 子树,所以我们只需要知道 curRight 的平衡因子,我们也就可以将parent 和 cur 的平衡因子跟新正确。
上面我们一直都没有说 curLeft 的平衡因子,其实curLeft 的平衡因子在第一次右单旋的时候就被跟新为了 0 ,而旋转结束后,curLeft 的平衡因子也就应该是 0.
左右双旋
这里我们就直接使用抽象图来描述了。
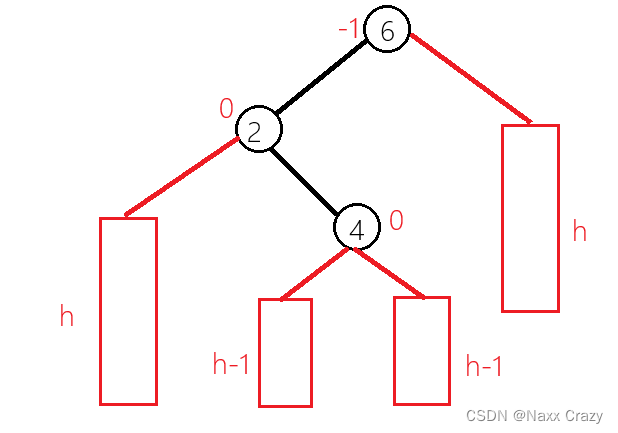
以上图为例,我们要插入一个值:
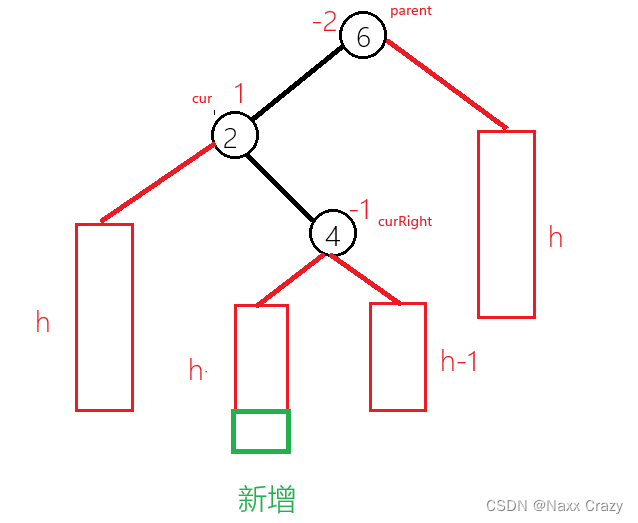
现在我们发现是左边高,但是我们知道这种情况下,我们单纯的使用右单旋是解决不了问题的,所以我们还是选哟使用双旋,也就是左右双旋,我们先对cur 节点进行左单旋,然后对parent 进行右单旋:
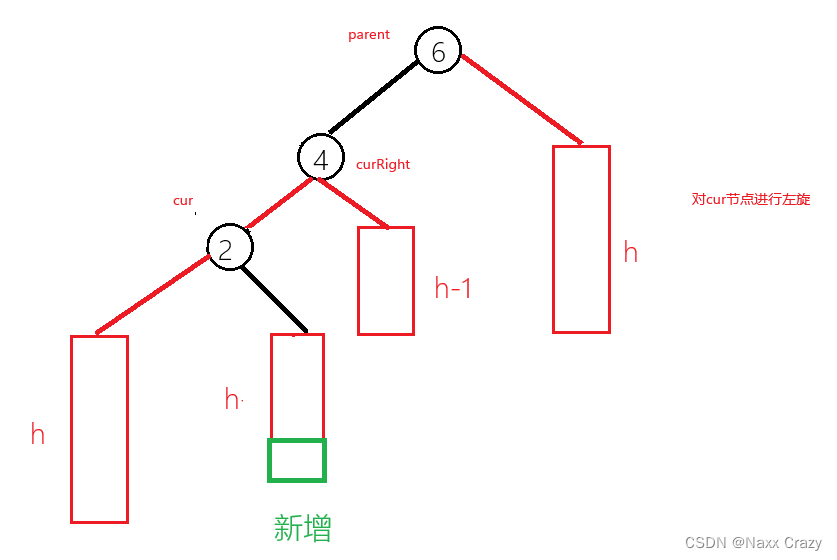
旋转后,我们发现现在是单纯的左边高,所以我们对 parent 节点使用右单旋:
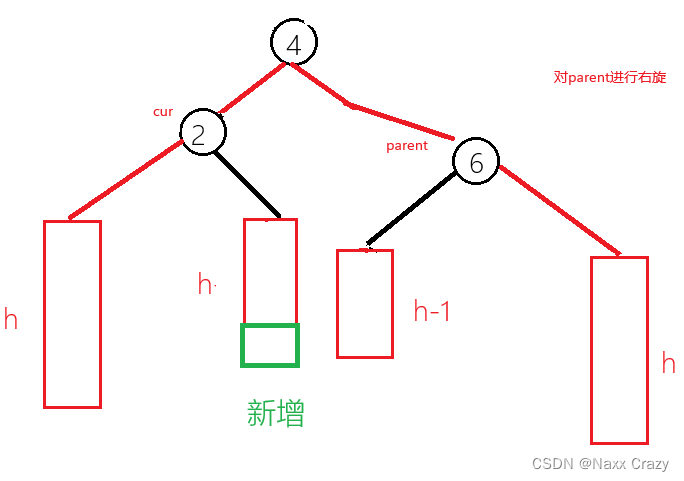
这时候的 parent cur 以及 curRight 的平衡因子都被跟新为 0了 ,但是都是 0 并不正确,而是也像我们前面的右左双一样,需要看 curRight 的平衡因子:
1. 如果插入到 curRight 的keft,那么 cur 的平衡因子就是 0 ,parent 的平衡因子为 1。
2. 如果插入到 curRight 的 right ,那么 cur 的平衡因子就是 -1,parent 的平衡因子就是 0。
总结
- 如果 parent 的平衡因子为 2 ,cur 的平衡因子为 1,那么使用的是左单旋,将 parent 和 cur 的平衡因子都跟新为 0.
- 如果 parent 的平衡因子为 -2 ,cur 的平衡因子为 -1,那么使用的是右单,将 parent 和 cur 的平衡因子都跟新为 0.。
- 如果 parent 的平衡因子为 2 ,cur 的平衡因子为 -1,那么使用的是右左双旋 平衡因子: 如果curLeft 的平衡因子为 1 ,那么就将parent 的平衡因子置为 -1,cur 的平衡因子置为 0,curLeft 的平衡因子为 0 如果curLeft 的平衡因子为 -1 ,那么就将parent 的平衡因子置为 0,cur 的平衡因子置为 1,curLeft 的平衡因子为 0 如果curLeft 的平衡因子为 0 ,那么就将parent 的平衡因子置为 0,cur 的平衡因子置为 0,curLeft 的平衡因子为 0
- 如果 parent 的平衡因子为 -2 ,cur 的平衡因子为 1,那么使用的是左右双旋 平衡因子: 如果curRight的平衡因子为 1 ,那么就将parent 的平衡因子置为 0,cur 的平衡因子置为 -1,curRight的平衡因子为 0 如果curRight的平衡因子为 -1 ,那么就将parent 的平衡因子置为 1,cur 的平衡因子置为 0,curRight的平衡因子为 0 如果curRight的平衡因子为 0 ,那么就将parent 的平衡因子置为 0,cur 的平衡因子置为 0,curLeft 的平衡因子为 0
实现
上面大概率是把思路都说明白了,下面开始看一下实现:
插入实现
首先我们先看一下AVLTreeNode:
对于该节点,我们需要一个存储值的变量,我们还需要三个指针,其中一个 left,还有一个 right,还有一个 parent,这里需要parent 是因为我们需要找找到它的父亲节点,还需要一个平衡因子
template<class K, class V>
struct TreeNode
{pair<K, V> _kv;TreeNode<K, V>* _left;TreeNode<K, V>* _right;TreeNode<K, V>* _parent;int _balance;TreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr),_balance(0){}
};这里我们将存储值的变量之间设置为了 kv 结构,因为这样既可以适用于 set,也适用于 map.
下面就是插入:
插入的话,先按照搜索树的插入节点,也就是插入插入位置,然后记录其父亲节点:
if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{// 重复了,插入失败return false;}}// 插入数据cur = new Node(kv);if (kv.first < parent->_kv.first){//维护三叉链parent->_left = cur;cur->_parent = parent;}else{//维护三叉链parent->_right = cur;cur->_parent = parent;}等 cur 节点插入后,开始修正并检查平衡:
//检查平衡while (parent){//维护平衡因子// 平衡因子=右子树高度-左子树高度if (cur == parent->_left){parent->_balance--;}else{parent->_balance++;}// 检查 parent 的平衡因子// 如果为 0 说明parent 这颗树以及平衡,无需检查// 如果为 1/-1 说明 parent 的平衡发生了变化,说明需要检查 parent 的parent 的平衡因子// 如果为 2/-2 说明这棵树已经不平衡了,需要旋转if (parent->_balance == 0){//该树已经平衡break;}else if (parent->_balance == 1 || parent->_balance == -1){// 说明该树的高度发生变化,需要检查 parent 的 parent 的平衡因子,所以需要向上传递cur = parent;parent = parent->_parent;}else if (parent->_balance == 2 || parent->_balance == -2){// 说明该树需要旋转保持平衡if (parent->_balance == 2 && cur->_balance == 1){// 左单旋RotateL(parent);break;}else if (parent->_balance == -2 && cur->_balance == -1){// 右单旋RotateR(parent);break;}else if (parent->_balance == 2 && cur->_balance == -1){// 右左双旋RotateRL(parent);break;}else if (parent->_balance == -2 && cur->_balance == 1){// 左右双旋RotateLR(parent);break;}else{assert(0);}}else{// 不能出现该种情况assert(0);}}
上面就是修正并且检查平衡,那么我们看一下应该怎么样旋转:
左单旋实现
实际上,左单旋并不是像我们说的那样,只有我们前面模拟插入的时候的两步
主要步骤:
1. 将 parent 的 right 连接成 cur 的 left
2. 将 cur 的 left 连接成 parent
3. 维护三叉链
实际上我们还需要维护三叉链,也就是他们的父亲节点,。
// 左单旋void RotateL(Node* parent){Node* cur = parent->_right;Node* curLeft = cur->_left;parent->_right = curLeft;if (curLeft){curLeft->_parent = parent;}cur->_left = parent;Node* pparent = parent->_parent;parent->_parent = cur;if (pparent == nullptr){// parent 就是根节点_root = cur;cur->_parent = nullptr;}else{if (parent == pparent->_left){pparent->_left = cur;}else{pparent->_right = cur;}cur->_parent = pparent;}parent->_balance = 0;cur->_balance = 0;}右单旋实现
主要步骤:
1. 将 parent 的 left 链接到 cur 的 right
2.将 cur 的 left 链接到 parent
3. 维护其三叉链
//右单旋void RotateR(Node* parent){Node* cur = parent->_left;Node* curRight = cur->_right;parent->_left = curRight;if (curRight){curRight->_parent = parent;}cur->_right = parent;Node* pparent = parent->_parent;parent->_parent = cur;if (pparent == nullptr){// 说明 parent 是根节点_root = cur;cur->_parent = nullptr;}else{if (parent == pparent->_left){pparent->_left = cur;}else{pparent->_right = cur;}cur->_parent = pparent;}parent->_balance = 0;cur->_balance = 0;}右左双旋实现
主要步骤:
1. 对 cur 节点进行右旋
2. 对 parent 节点进行左旋
3. 修正平衡因子,这个我们前面总结过了
void RotateRL(Node* parent){//先对 cur 节点进行右单旋//在对 parent 节点进行左单旋Node* cur = parent->_right;Node* curLeft = cur->_left;int balance = curLeft->_balance;RotateR(cur);RotateL(parent);//旋转后维护平衡因子//这里右几种可能://1. curLeft 节点的平衡因子为 0//2. curLeft 节点的平衡因子为-1//3. curLeft 节点的平衡因子为 1// 这里发现每一次旋转结束后,curRight 节点的左树给了parent,右树给了 cur,// 所以这里需要的以区分新增节点插入到了 curRight 节点的左是右// 记录该平衡因子主要是为了维护旋转后的平衡因子if (balance == 0){// curRight 就是新增节点,所以cur,parent,curRight 的平衡因子都为 0cur->_balance = 0;parent->_balance = 0;curLeft->_balance = 0;}else if (balance == 1){// 新增在了右边,所以cur,parent,curRight 的平衡因子分别为 0,-1,0cur->_balance = 0;parent->_balance = -1;curLeft->_balance = 0;}else if (balance == -1){// 新增在了左边,所以cur,parent,curRight 的平衡因子分别为 1,0,0cur->_balance = 1;parent->_balance = 0;curLeft->_balance = 0;}else{assert(0);}}左右双旋实现
主要步骤:
1. 对 cur 节点进行左旋
2. 对 parent 节点进行右旋
3. 修正平衡因子,这个我们前面总结过了
// 左右双旋void RotateLR(Node* parent){Node* cur = parent->_left;Node* curRight = cur->_right;int balance = curRight->_balance;RotateL(cur);RotateR(parent);if (balance == 0){cur->_balance = 0;parent->_balance = 0;curRight->_balance = 0;}else if (balance == -1){cur->_balance = 0;parent->_balance = 1;curRight->_balance = 0;}else if (balance == 1){cur->_balance = -1;parent->_balance = 0;curRight->_balance = 0;}}相关文章:

AVL树 模拟实现(插入)
目录 模拟插入节点 左单旋 右单旋 右左双旋 左右双旋 总结 实现 插入实现 左单旋实现 右单旋实现 右左双旋实现 左右双旋实现 AVL树 模拟实现(插入) AVL 树,是高度平衡二叉搜索树,其主要通过旋转来控制其左右子树的高…...
《JavaSE》)
Java面试整理(三)《JavaSE》
反射机制(低) 在我刚开始学Java的时候,大家都很难理解反射这个概念,在实际开发中,虽然都有反射的踪影,但感觉自己又能理解是的。反射机制是指在程序运行时,对任意一个类都能获取其所有属性和方法,并且对任意一个对象都能调用其任意一个方法。 反射的步骤如下: 获取想要…...
LeetCode 1282. Group the People Given the Group Size They Belong To【哈希表】1267
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
Vue2项目练手——通用后台管理项目第八节
Vue2项目练手——通用后台管理项目 菜单权限功能tab.jsLogin.vueCommonAside.vuerouter/index.js 权限管理问题解决router/tab.jsCommonHeader.vuemain.js 菜单权限功能 不同的账号登录,会有不同的菜单权限通过url输入地址来显示页面对于菜单的数据在不同页面之间的…...

leetcode872. 叶子相似的树(java)
叶子相似的树 题目描述递归 题目描述 难度 - 简单 leetcode - 872. 叶子相似的树 请考虑一棵二叉树上所有的叶子,这些叶子的值按从左到右的顺序排列形成一个 叶值序列 。 举个例子,如上图所示,给定一棵叶值序列为 (6, 7, 4, 9, 8) 的树。 如果…...
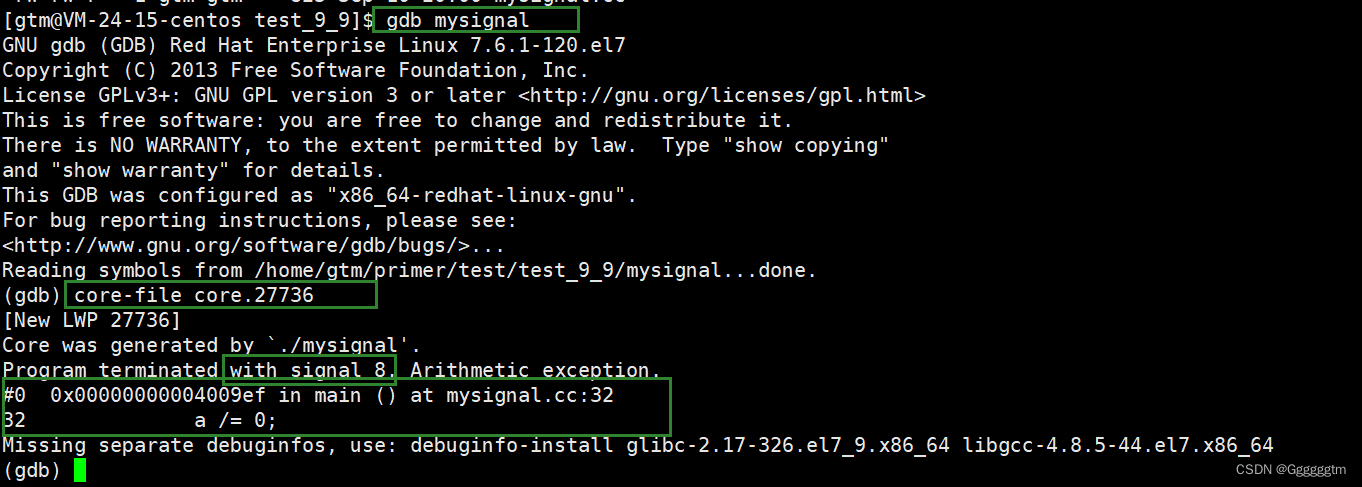
【Linux从入门到精通】信号(初识信号 信号的产生)
本篇文章会对Linux下的信号进行详细解释。主要内容是什么是信号、信号的产生、核心转储等问题。希望本篇文章会对你有所帮助。 文章目录 引入 一、初识信号 1、1 生活中的信号 1、2 Linux 下的信号 1、3 信号进程所得的初识结论 二、信号的产生 2、1 用户通过终端输入产生信号 …...
)
Golang综合项目实战(一)
Golang综合项目实战(一) 01-项目简介02-项目架构、术语、运行结果03-创建并初始化项目04-创建用户模型和错误处理05-创建密码加密工具类06-保存密码之前的hooks07-创建用户名密码验证工具类08-用户数据库操作逻辑09-操作用户service10-创建商品分类模型…...

springmvc 获取项目中的所有请求路径
springboot/springmvc 获取项目中的所有请求路径 1. 编写业务代码 Autowiredprivate WebApplicationContext applicationContext;GetMapping("/getAllURL")public RestfulResult getAllURL() {// 获取springmvc处理器映射器组件对象 RequestMappingHandlerMapping无…...

【React学习】React高级特性
1. 函数式组件和类组件区别 函数式组件 函数式组件是一种简单的组件定义方式,它是一个以JavaScript函数为基础的组件。 可以把函数式组件理解为纯函数,它的输入为props,输出为JSX。函数式组件没有状态,也没有生命周期。 functio…...
如何在Windows系统搭建filebrowser私人网盘并实现在外网访问本地内网
Windows系统搭建网盘神器filebrowser结合内网穿透实现公网访问 文章目录 Windows系统搭建网盘神器filebrowser结合内网穿透实现公网访问前言1.下载安装File Browser2.启动访问File Browser3.安装cpolar内网穿透3.1 注册账号3.2 下载cpolar客户端3.3 登录cpolar web ui管理界面3…...
)
蓝桥杯官网练习题(算式900)
题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 小明的作业本上有道思考题: 看下面的算式: (□□□□-□□□□)*□□900其中的小方块代表 0 ~ 9 的数字,这 10 个方块刚好包含了…...
)
【C++从入门到精通】第1篇:C++基础知识(上)
文章目录 1.1 C语句和程序结构1.1.1 本篇介绍1.1.2 语句1.1.3 函数和主函数1.1.4 解析Hello world1.1.5 语法和语法错误1.1.6 练习时间 1.2 注释1.2.1 单行注释1.2.2 多行注释1.2.3 正确使用注释1.2.4 注释掉代码 1.3 对象和变量1.3.1 数据和值1.3.2 对象和变量1.3.3 变量实例化…...

liunx系统无sudo或管理员权限安装rar解压安装包
liunx无sudo权限安装rar解压安装包 (1)正常liunx安装rar(2)无sudo\root(管理员身份)时如何安装rar (1)正常liunx安装rar 1、下载安装包 WinRAR archiver, a powerful tool to process RAR and ZIP files (r…...
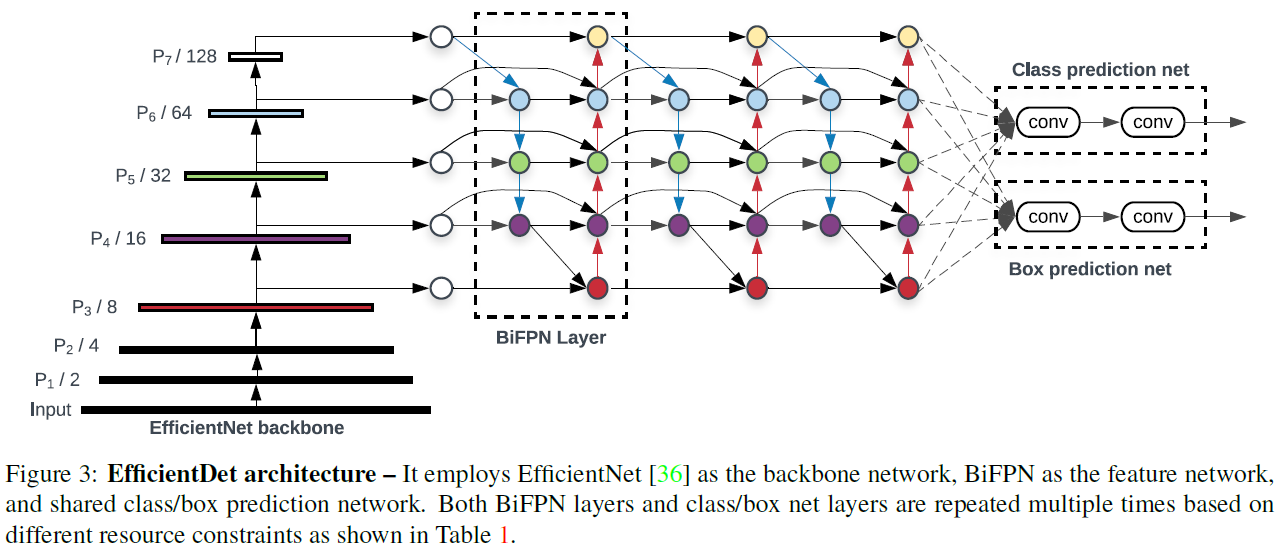
浅析目标检测入门算法:YOLOv1,SSD,YOLOv2,YOLOv3,CenterNet,EfficientDet,YOLOv4
本文致力于让读者对以下这些模型的创新点和设计思想有一个大体的认识,从而知晓YOLOv1到YOLOv4的发展源流和历史演进,进而对目标检测技术有更为宏观和深入的认知。本文讲解的模型包括:YOLOv1,SSD,YOLOv2,YOLOv3,CenterNet,EfficientDet,YOLOv4…...

C++:类和对象(三)
本文主要介绍初始化列表、static成员、友元、内部类、匿名对象、拷贝对象时编译器的优化。 目录 一、再谈构造函数 1.构造函数体赋值 2.初始化列表 3.explicit关键字 二、static成员 1.概念 2.特性 三、友元 1.友元函数 2.友元类 四、内部类 五、匿名对象 六、拷…...

分布式系统第三讲:全局唯一ID实现方案
分布式系统第三讲:全局唯一ID实现方案 本文主要介绍常见的分布式ID生成方式,大致分类的话可以分为两类:一种是类DB型的,根据设置不同起始值和步长来实现趋势递增,需要考虑服务的容错性和可用性; 另一种是类snowflake型…...

Ubuntu之apt-get系列--安装JDK8--方法/教程
原文网址:Ubuntu之apt-get系列--安装JDK8--方法/教程_IT利刃出鞘的博客 简介 本文介绍如何在Ubuntu下安装JDK8。 验证是否安装 可以通过如下命令判断系统是否有安装ssh服务: 命令 java -version 结果 如上所示,表示还没有安装。 查看…...

npm 实现原理
输入 npm install 命令并敲下回车后,会经历如下几个阶段(以 npm 5.5.1 为例): 1.执行工程自身 preinstall 当前 npm 工程如果定义了 preinstall 钩子此时会被执行。 2.确定首层依赖模块 首先需要做的是确定工程中的首层依赖&a…...

国家开放大学 练习题
学前儿童社会教育活动指导 参考试题 一、单项选择题(每小题3分,共30分) 1.《规程》第三十二条规定:“幼儿园应当充分尊重幼儿的个体差异,根据幼儿不同的心理 发展水平,研究有效的活动形式和方法&am…...

Kotlin
函数命名 针对您目前为止学到的 Kotlin 知识,下面给出了一些相关样式指南: 函数名称应采用驼峰式大小写形式,并且应该是动词或动词短语。每个语句都应单独占一行。左花括号应出现在函数开始行的末尾。左花括号前应有一个空格。 变量声明 变…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...
