【数据结构】红黑树的插入与验证
文章目录
- 一、基本概念
- 1.时代背景
- 2. 基本概念
- 3.基本性质
- 二、实现原理
- 1. 插入
- 1.1变色
- 1.2旋转+变色
- ①左旋
- ②右旋
- ③右左双旋
- ④左右双旋
- 2.验证
- 源码
- 总结
一、基本概念
1.时代背景
- 1972年鲁道夫·拜尔(Rudolf Bayer)发明了一种数据结构,这是一种特殊的B树4阶情况。这些树保持了从根到叶的所有路径,节点数量相同,创造了完美平衡的树。但是,它们不是二叉搜索树。拜耳在他的论文中称它们为“对称二元B树”。这是红黑树的起源。

- 在1978年的一篇论文“平衡树的二色框架”中,列奥尼达斯·吉巴斯(Leonidas J. Guibas )和罗伯特·塞奇威克(Robert Sedgewick)从对称的二元B树中推导出了红黑树。选择“红色”是因为它是作者在施乐PARC工作时可用的彩色激光打印机产生的最好看的颜色。吉巴斯的另一个回应说,这是因为他们可以使用红色和黑色的笔来画树。


第一张为——列奥尼达斯·吉巴斯,第二张为——罗伯特·塞奇威克。
- 1993年,Arne Andersson引入了右倾树的想法,以简化插入和删除操作。

- 1999年,Chris Okasaki展示了如何使插入操作纯粹功能化。它的平衡功能只需要处理 4 个不平衡情况和一个默认平衡情况。

详细请看:维基百科
2. 基本概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或
Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路 径会比其他路径长出俩倍,因而是接近平衡的。
- 实现平衡的关键:
最长路径小于等于最短路径的两倍。
3.基本性质
- 每个结点不是红色就是黑色
根节点是黑色的如果一个节点是红色的,则它的两个孩子结点是黑色的(如果一个结点是黑色的,则其两个孩子可以是红的也可以是黑的。)对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
强调:2,3,4点是有关联的,且是最关键的3点。
- 假设根节点如果是红的,那么插入的结点就是只能是黑的(3),那么就违背了(4)。
- 对于3分析,孩子结点为空,但空节点也被理解成黑色(5),因此(5)是用来辅助(3)的。
- 对于4分析,可推理出两个结论——
1 . 插入结点必须为红色的。
2 . 满足最长路径小于最短路径的两倍(概念)。对此点可以看做间隔问题,即n个数之间(不算头一个数),有n个间隔,即n个黑结点(不算根节点),之间最多有n个红结点。
二、实现原理
1. 插入
1.1变色
根本逻辑:基于每条路径的黑色结点不变。
第一种变色方式:
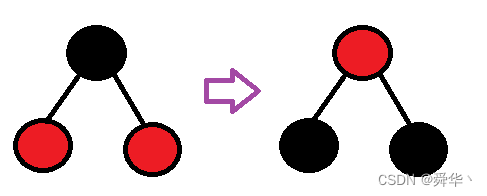
这样变,是不是每条路径的黑色结点数没变呢?
那这样变的前提是什么呢?
- 黑色结点的左右孩子为红且不为空。
那什么时候发生变色呢?
- 基于性质3,红色结点的两个孩子必须为黑,但由4我们可以推出每次插入结点必须为红,那这时候我们按照4的原则进行处理,使处理结果符合3即可,怎么处理,就是进行变色。
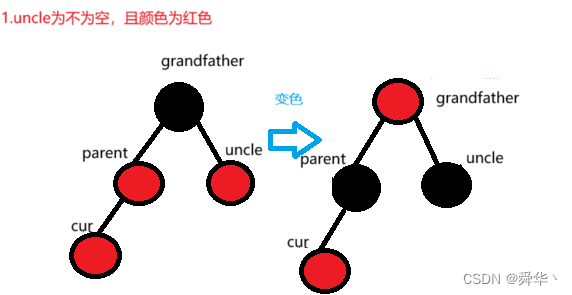
此时,parent的右边进行插入新节点,且parent在grandfather的左边。
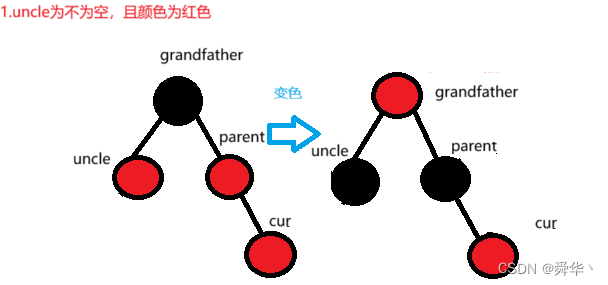
此时在parent的右边进行插入,且parent为grandfather的左节点。
- 总结
- 变色的前提是每条路径的黑色结点不变
- uncle非空且为红,且parent为红,变grandfather为红,parent与uncle为黑。
继续分析,如果grandfather为红,其父节点是否可能为红呢?
- 答案是可能的。
因此我们需要继续往上更新:
- 更新cur为grandfather
- parent为cur的parent
接着分析,如果grandfather为根节点呢?
- 由于性质2,我们需要再次修改根节点的颜色为黑。
1.2旋转+变色
前面我们分析了一种简单的只需变色的情况,我们下面接着分析另外一种情况。
第二种变色需要在旋转的基础上进行分类讨论,具体情况有四种。
①左旋
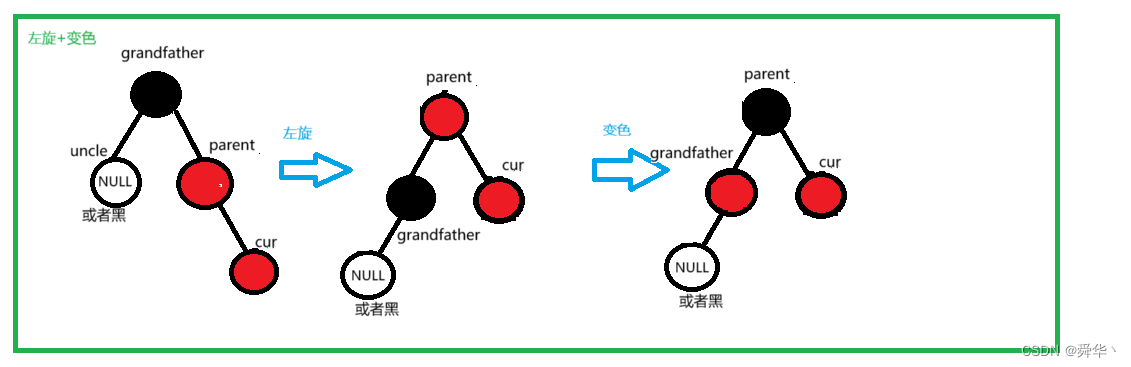
补充:当uncle为黑结点时,parent的左子树不为空且根节点为黑色,cur的左右子树同理,这里不过多分析了,因为具体情况过多分析容易提高理解难度。
- 开始时parent在grandfather右边,且cur在parent的右边
②右旋
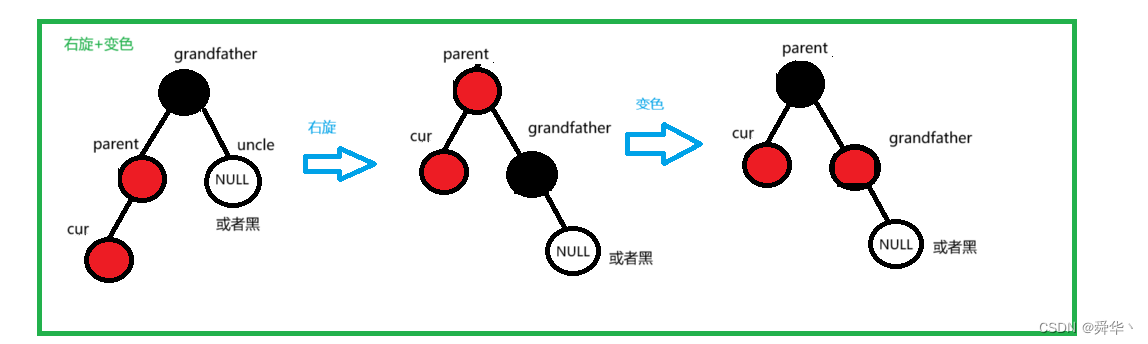
对uncle的补充同左旋
- 开始时parent在grandfather左边,且cur在parent的左边
③右左双旋
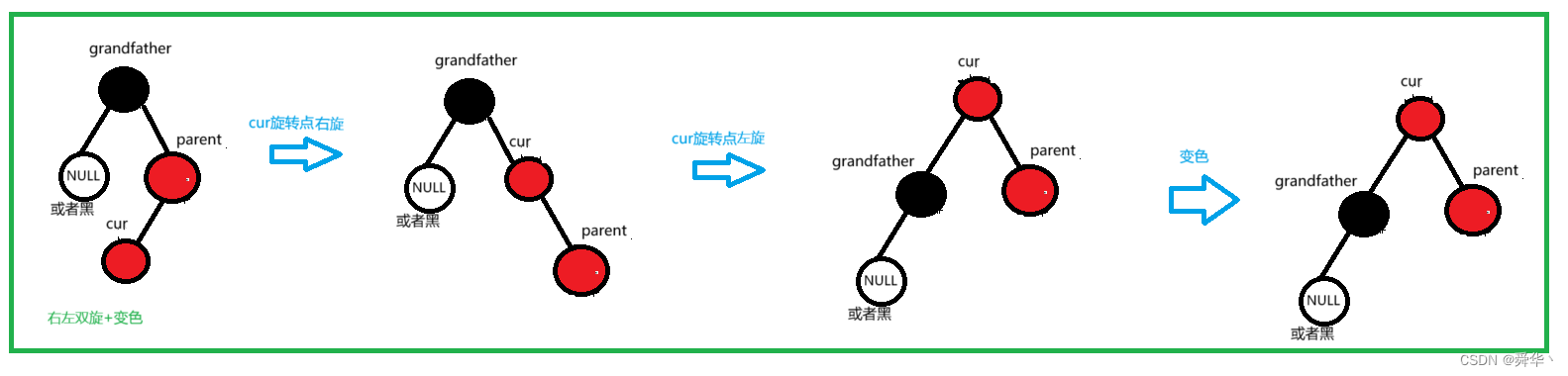
对uncle的补充同左旋
- 开始时parent在grandfather的右边,且cur在parent的左边
④左右双旋
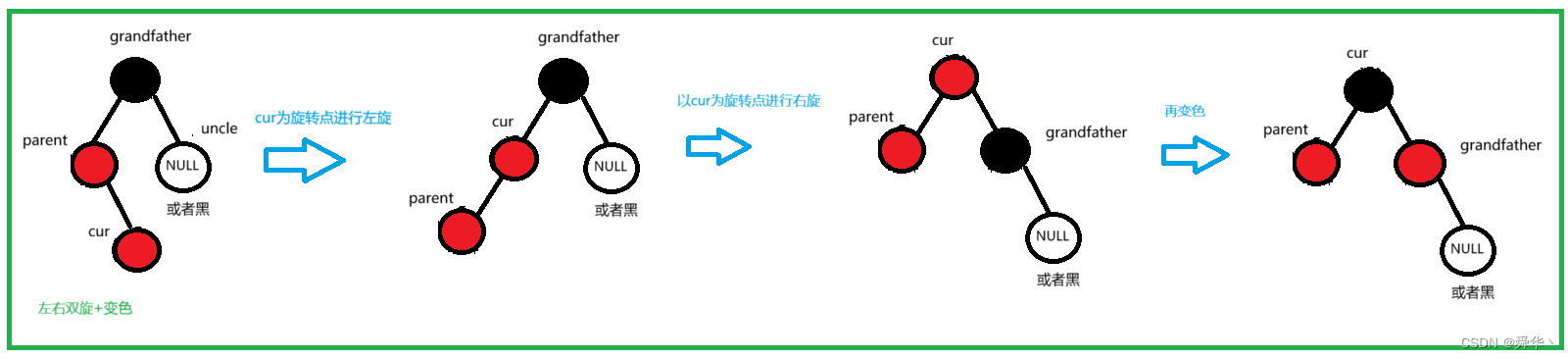
对uncle的补充同左旋
-
开始时parent在grandfather的左边,且cur在parent的右边
-
总结
根据parent的位置我们可以大致分为两种情况:
-
parent在grandfather的左边
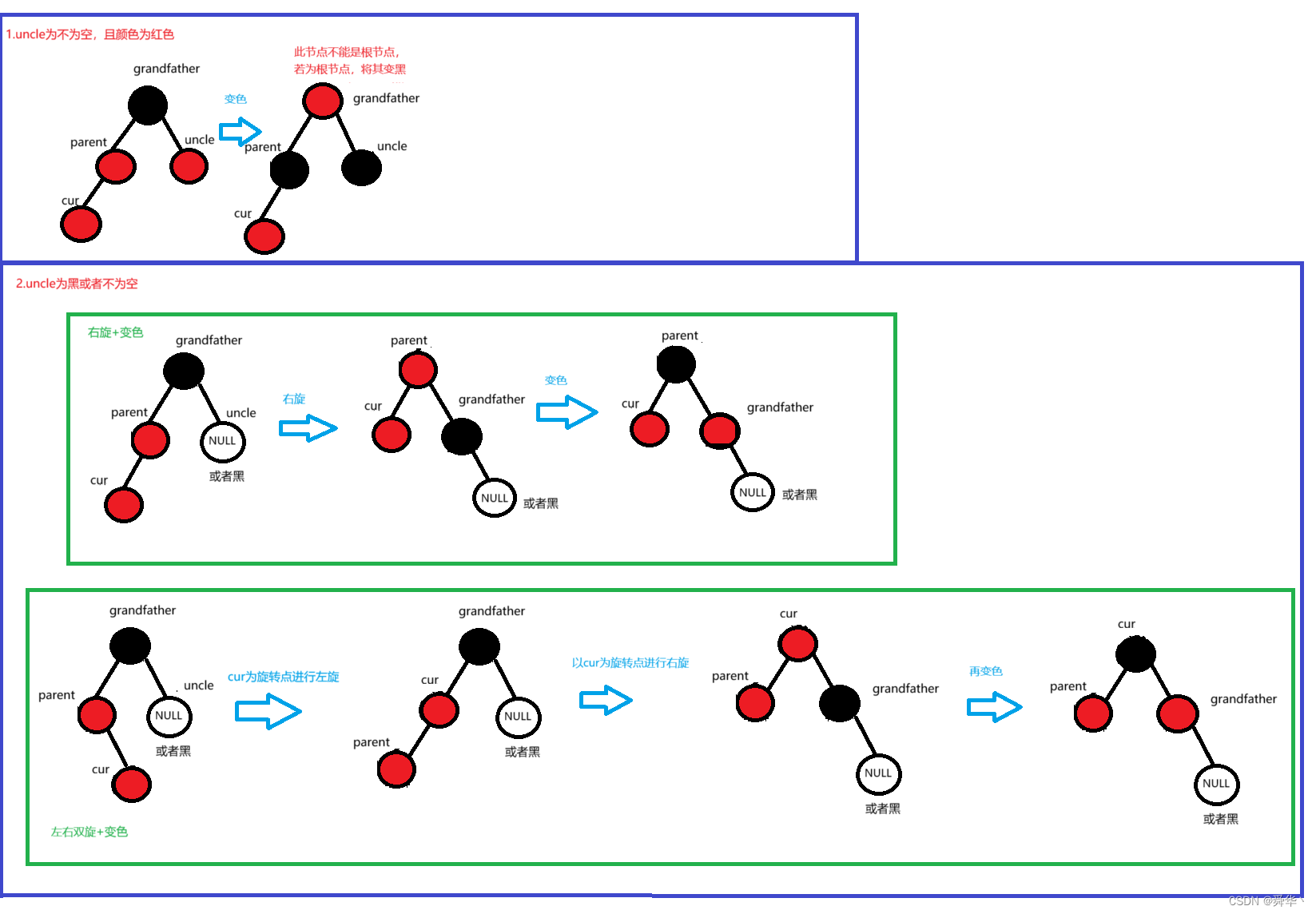
-
parent在grand的右边
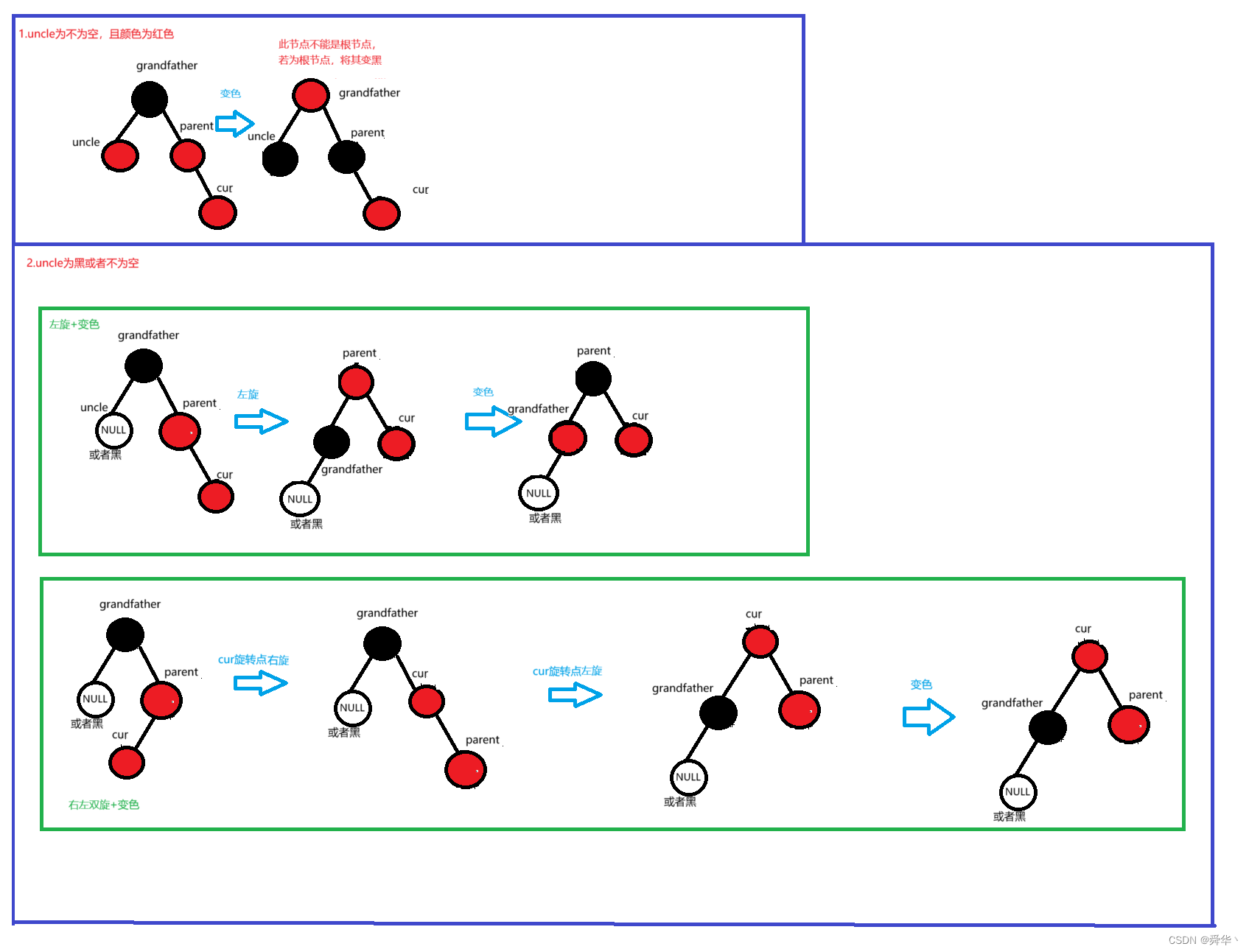
其实不难看出,AVL和红黑树都会进行旋转,只是AVL树旋转后处理的是平衡因子,红黑树旋转后处理的是变色,归根结底终究都是为了让树达到平衡。
- 核心代码
//判断是否要进行旋转变色
//当父节点为红色说明要进行判断
while (parent && parent->_col == RED)
{//爷爷结点Node* grandfather = parent->_parent;if (grandfather->_left == parent){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED)//如果uncle存在且为红色{//变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续往上迭代进行分析cur = grandfather;parent = cur->_parent;}else//如果uncle不存在或者为黑色{//旋转if (parent->_left == cur){RotateR(grandfather);parent->_col = BLACK;cur->_col = grandfather->_col = RED;}else{RotateL(parent);RotateR(grandfather);cur->_col = BLACK;parent->_col = grandfather->_col = RED;}break;}}else//grandfather->_right == parent{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){//变色grandfather->_col = RED;parent->_col = uncle->_col = BLACK;//往上更新cur = grandfather;parent = cur->_parent;}else{if (parent->_right == cur){//旋转RotateL(grandfather);//变色parent->_col = BLACK;grandfather->_col = cur->_col = RED;}else{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = parent->_col = RED;}break;}}
}
- 插入代码
bool insert(const pair<Key, Val>& val)
{//第一步:插入操作//如果根节点为空if (_root == nullptr){_root = new Node(val);_root->_col = BLACK;return true;}else{Node* cur = _root, * parent = _root;while (cur){if (cur->_key > val.first){parent = cur;cur = cur->_left;}else if (cur->_key < val.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(val);if (parent->_key > val.first){parent->_left = cur;}else{parent->_right = cur;}//更新新增结点的_parentcur->_parent = parent;//判断是否要进行旋转变色//当父节点为红色说明要进行判断while (parent && parent->_col == RED){//爷爷结点Node* grandfather = parent->_parent;if (grandfather->_left == parent){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED)//如果uncle存在且为红色{//变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续往上迭代进行分析cur = grandfather;parent = cur->_parent;}else//如果uncle不存在或者为黑色{//旋转if (parent->_left == cur){RotateR(grandfather);parent->_col = BLACK;cur->_col = grandfather->_col = RED;}else{RotateL(parent);RotateR(grandfather);cur->_col = BLACK;parent->_col = grandfather->_col = RED;}break;}}else//grandfather->_right == parent{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){//变色grandfather->_col = RED;parent->_col = uncle->_col = BLACK;//往上更新cur = grandfather;parent = cur->_parent;}else{if (parent->_right == cur){//旋转RotateL(grandfather);//变色parent->_col = BLACK;grandfather->_col = cur->_col = RED;}else{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = parent->_col = RED;}break;}}}//根节点可能为红色,不管红色还是黑色都弄成黑色_root->_col = BLACK;return true;}
}
2.验证
- 原理
- 根节点不能为红
- 每条路径的黑色结点数相同
- 每条路径不能出现连续的红色结点。
- 代码
bool _IsRBTree(Node* root)
{if (root == nullptr)return true;//根节点是黑色的if (root->_col == RED)return false;//各个路径的黑色结点数是相同的,因此设立一个基准进行比较合适,//再对树进行遍历求每个路径的黑色结点的数量,最后比较即可。int benchmark = 0;Node* cur = root;while (cur){if (cur->_col == BLACK)benchmark++;cur = cur->_left;}return Check(root);
}
bool Check(Node* root, int BCount,int benchmark)
{if (root == nullptr){//验证基准值是否等于黑色结点数//只要有一个不是,即不是红黑树。if (BCount != benchmark)return false;return true;}//求每条黑色结点的个数if (root->_col == BLACK)BCount++;//验证性质3,即不能有连续的红色结点。if (root->_col == RED && root->_parent && root->_parent->_col == RED){return false;}return Check(root->_left,BCount,benchmark) && Check(root->_right, BCount, benchmark);
}
源码
#pragma once
#include<iostream>
using namespace std;
namespace MY_STL
{enum Color{RED = 0,BLACK = 1};template<class Key,class Val>struct RBTreeNode{typedef RBTreeNode<Key, Val> Node;RBTreeNode(const pair<Key,Val>& key):_key(key.first),_val(key.second),_right(nullptr),_left(nullptr),_parent(nullptr),_col(RED){}Node* _right;Node* _left;Node* _parent;Key _key;Val _val;Color _col;};template<class Key,class Val>class RBTree{typedef RBTreeNode<Key, Val> Node;public:bool insert(const pair<Key, Val>& val){//第一步:插入操作//如果根节点为空if (_root == nullptr){_root = new Node(val);_root->_col = BLACK;return true;}else{Node* cur = _root, * parent = _root;while (cur){if (cur->_key > val.first){parent = cur;cur = cur->_left;}else if (cur->_key < val.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(val);if (parent->_key > val.first){parent->_left = cur;}else{parent->_right = cur;}//更新新增结点的_parentcur->_parent = parent;//判断是否要进行旋转变色//当父节点为红色说明要进行判断while (parent && parent->_col == RED){//爷爷结点Node* grandfather = parent->_parent;if (grandfather->_left == parent){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED)//如果uncle存在且为红色{//变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续往上迭代进行分析cur = grandfather;parent = cur->_parent;}else//如果uncle不存在或者为黑色{//旋转if (parent->_left == cur){RotateR(grandfather);RotateCount++;parent->_col = BLACK;cur->_col = grandfather->_col = RED;}else{RotateL(parent);RotateR(grandfather);RotateCount+=2;cur->_col = BLACK;parent->_col = grandfather->_col= RED;}break;}}else//grandfather->_right == parent{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){//变色grandfather->_col = RED;parent->_col = uncle->_col = BLACK;//往上更新cur = grandfather;parent = cur->_parent;}else{if (parent->_right == cur){//旋转RotateL(grandfather);RotateCount++;//变色parent->_col = BLACK;grandfather->_col = cur->_col = RED;}else{RotateR(parent);RotateL(grandfather);RotateCount += 2;cur->_col = BLACK;grandfather->_col = parent->_col = RED;}break;}}}//根节点可能为红色,不管红色还是黑色都弄成黑色_root->_col = BLACK;return true;}}bool IsRBTree(){return _IsRBTree(_root);}size_t Height(){return Height(_root);}private:size_t Height(Node* root){if (root == nullptr){return 0;}int LHeight = Height(root->_left);int RHeight = Height(root->_right);return max(LHeight, RHeight) + 1;}bool _IsRBTree(Node* root){if (root == nullptr)return true;//根节点是黑色的if (root->_col == RED)return false;//各个路径的黑色结点数是相同的,因此设立一个基准进行比较int benchmark = 0;Node* cur = root;while (cur){if (cur->_col == BLACK)benchmark++;cur = cur->_left;}return Check(root,0,benchmark);}bool Check(Node* root, int BCount,int benchmark){if (root == nullptr){//验证基准值是否等于黑色结点数//只要有一个不是,即不是红黑树。if (BCount != benchmark)return false;return true;}//求每条黑色结点的个数if (root->_col == BLACK)BCount++;//验证性质3,即不能有连续的红色结点。if (root->_col == RED && root->_parent && root->_parent->_col == RED){return false;}return Check(root->_left,BCount,benchmark) && Check(root->_right, BCount, benchmark);}void RotateL(Node* parent){//画图分析://操作的结点有cur,cur_left,ppnodeNode* cur = parent->_right;Node* cur_left = cur->_left;//将parent的右节点改为cur_leftparent->_right = cur_left;//改变cur_left父节点的转向//cur_left可能为空if (cur_left != nullptr){cur_left->_parent = parent;}//将parent链接在cur的左边//为了更新cur的parent需要保存parent的父节点Node* ppnode = parent->_parent;cur->_left = parent;parent->_parent = cur;//ppnode可能为空if (ppnode == nullptr){//需要修改根节点_root = cur;cur->_parent = nullptr;}else{//改变ppnode的指向if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}void RotateR(Node* parent){//操作的结点Node* cur = parent->_left;Node* cur_right = cur->_right;//第一步:将cur_right链接到parent的leftparent->_left = cur_right;//更改cur_right的父节点//注意:cur_right可能为空if (cur_right != nullptr){cur_right->_parent = parent;}//第二步:将parent链接到cur的右结点。//先保存一下parent的父节点Node* ppnode = parent->_parent;cur->_right = parent;parent->_parent = cur;//ppnode为空说明需要修改根节点if (ppnode == nullptr){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}Node* _root = nullptr;public:size_t RotateCount = 0;};
};
总结
红黑树的理解较AVL树抽象,需要画图分析,不过有了AVL树旋转的基础,这里的难度要下降不少。还是与之前一样,只要图画的好,代码跑不了,所以这里的关键就在于画图。
总之,今天的分享到这里就结束了,如果感觉有所帮助,不妨点个赞鼓励一下吧!
相关文章:

【数据结构】红黑树的插入与验证
文章目录 一、基本概念1.时代背景2. 基本概念3.基本性质 二、实现原理1. 插入1.1变色1.2旋转变色①左旋②右旋③右左双旋④左右双旋 2.验证 源码总结 一、基本概念 1.时代背景 1972年鲁道夫拜尔(Rudolf Bayer)发明了一种数据结构,这是一种特殊的B树4阶情况。这些树…...
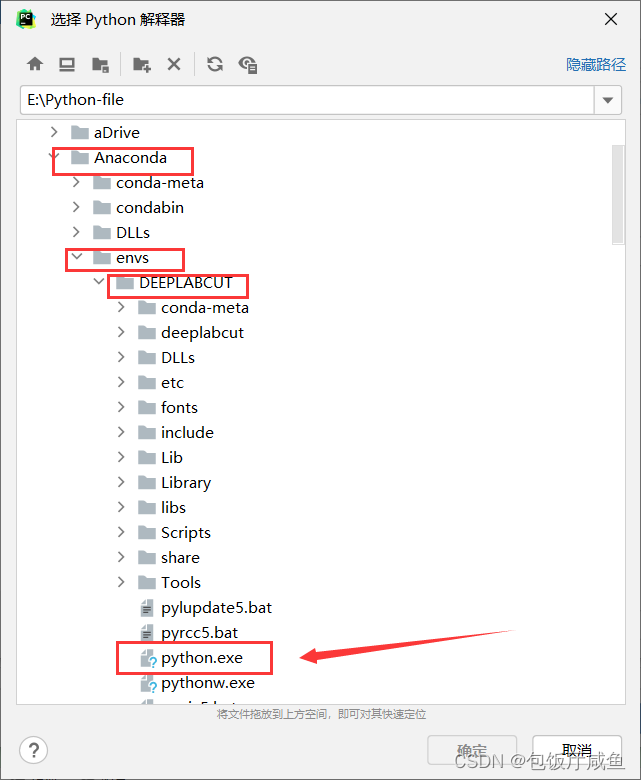
Pycharm----将Anaconda建立的环境导入
首先打开项目设置,点击添加 随后点击现有环境,点击三个。。。号进行添加 最后找到你Anaconda安装文件夹,envs找到你建立的环境名称,找到python.exe将它导入即可让现在的python环境为你建立的环境,同时还需要更改终端方…...

数字花园的指南针:微信小程序排名的提升之道
微信小程序,是一片数字花园,其中各种各样的小程序竞相绽放,散发出各自独特的芬芳。在这个花园中,排名优化就像是精心照料花朵的园丁,让我们一同走进这个数字花园,探寻如何提升微信小程序的排名优化…...

LRU与LFU的c++实现
LRU 是时间维度上最少使用 维持一个链表,最近使用的放在表头 淘汰表尾 LFU 是实际使用频率的最少使用 每一个对应的频率维持一个链表, 淘汰最低频率的最后一个 1. LRU LRU(Least Recently Used,最近最少使用)是一种常…...

什么是Docker和Docker-Compose?
Docker的构成 Docker仓库:https://hub.docker.com Docker自身组件 Docker Client:Docker的客户端 Docker Server:Docker daemon的主要组成部分,接受用户通过Docker Client发出的请求,并按照相应的路由规则实现路由分发…...
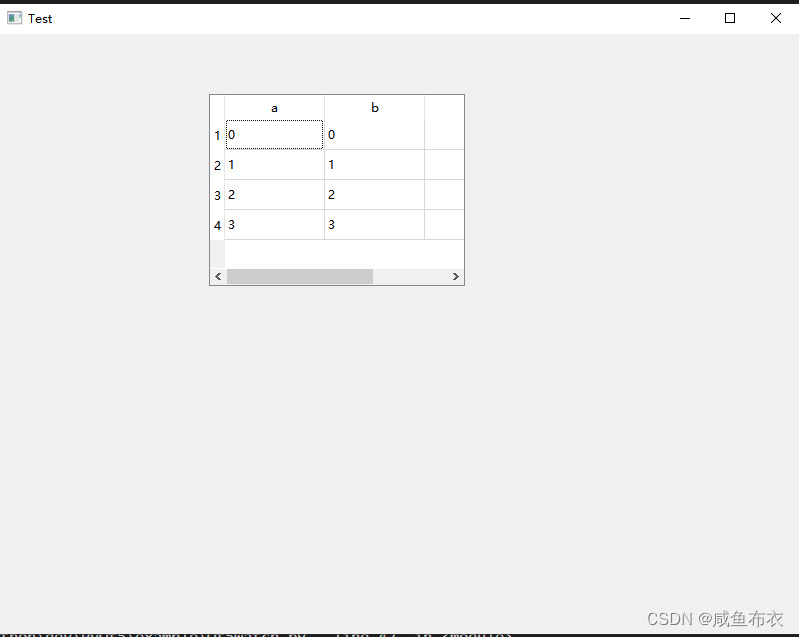
三.listview或tableviw显示
一.使用qt creator 转变类型 变形为listview或tableviw 二.导出ui文件为py文件 # from123.py 为导出 py文件 form.ui 为 qt creator创造的 ui 文件 pyuic5 -o x:\xxx\from123.py form.uifrom123.py listview # -*- coding: utf-8 -*-# Form implementation generated fro…...
【算法】一文带你从浅至深入门dp动态规划
文章目录 一、前言二、动态规划理论基础1、基本概念2、动态规划五部曲【✔】3、出错了如何排查? 三、实战演练🗡0x00 斐波那契数0x01 第N个泰波那契数0x02 爬楼梯0x03 三步问题0x04 使用最小花费爬楼梯⭐解法一解法二 0x05 解码方法* 四、总结与提炼 一、…...

超简单免费转换ape到flac
1. 安装最新版的ffmpeg 2. 安装cywin环境 3. 设置path到ffmpeg export PATH$PATH:"PATH/TO/FFMPEG/BIN" 4.到ape所在的目录,执行以下命令 find . -iname "*.ape" | while read line; do fb${line::-4}; fn"$fb.flac";echo ffm…...

JavaScript混淆加密
什么是JS混淆加密? JavaScript混淆加密是一种通过对源代码进行变换,使其变得难以理解和分析的技术。它的目标是增加攻击者破解代码的难度,同时保持代码的功能不受影响。混淆加密的目的是使代码难以逆向工程,从而防止攻击者窃取知…...
Java8特性-Lambda表达式
📕概述 在Java 8中引入了Lambda表达式作为一项重要的语言特性,可以堪称是一种语法糖。Lambda表达式使得以函数式编程的方式解决问题变得更加简洁和便捷。 Lambda表达式的语法如下: (parameters) -> expression (参数) -> {代码}其中&…...
通过Power Platform自定义D365CE业务需求 - 1. Microsoft Power Apps 简介
Microsoft Power Apps是一个趋势性的、无代码和无代码的商业应用程序开发平台,配有一套应用程序、服务和连接器。其数据平台为构建适合任何业务需求的自定义业务应用程序提供了快速开发环境。随着无代码、少代码应用程序开发的引入,任何人都可以快速构建低代码应用程序,并与…...
简易实现QT中的virtualkeyboard及问题总结
文章目录 前言:一、虚拟键盘的实现综合代码 二、为什么选用QWidget而不适用QDialog实现键盘三、从窗体a拉起窗体b后,窗体b闪退问题的探讨四、关闭主窗口时子窗口未关闭的问题 前言: 本文章主要包含四部分: 虚拟键盘的实现&#…...

景联文科技可为多模态语音翻译模型提供数据采集支持
8月22日Facebook的母公司Meta Platforms发布了一种能够翻译和转录数十种语言的人工智能模型——SeamlessM4T,可以在日常生活中或者商务交流中为用户提供更便捷的翻译和转录服务。 相较于传统的文本翻译,这项技术的最大区别在于它可以实现端到端的语音翻译…...

定时器分批请求数据
<!DOCTYPE html> <html><script>//需要分页的数组let arr [1,2,3,4,5,6,7,8,9,10]//分割数组,每页3条splitArr(arr,4)/*** 分割数组*/function splitArr(idList,size){//当前页数let num 1//共多少页let count Math.ceil(idList.length / siz…...

【华为OD机试python】报数游戏【2023 B卷|100分】
【华为OD机试】-真题 !!点这里!! 【华为OD机试】真题考点分类 !!点这里 !! 题目描述 100个人围成一圈,每个人有一个编码,编号从1开始到100。 他们从1开始依次报数,报到为M的人自动退出圈圈,然后下一个人接着从1开始报数, 直到剩余的人数小于M。 请问最后剩余的人在原先…...
【深度学习实战—6】:基于Pytorch的血细胞图像分类(通用型图像分类程序)
✨博客主页:米开朗琪罗~🎈 ✨博主爱好:羽毛球🏸 ✨年轻人要:Living for the moment(活在当下)!💪 🏆推荐专栏:【图像处理】【千锤百炼Python】【深…...

华清远见第六课程day4作业
仿照string类,完成myString 类 #include <iostream> #include <cstring>using namespace std;class myString{ private:char *str;int size; public:myString():size(10){str new char[size];strcpy(str,"");}myString(const char*s){size …...

【广州华锐互动】AR远程智慧巡检在化工行业中的应用
AR远程智慧巡检是一种基于增强现实技术的新型巡检方式,它可以利用虚拟信息和现实场景的结合,实现对设备、工艺流程等方面的实时监测和识别。在化工行业中,AR远程智慧巡检具有广泛的应用前景,可以提高生产效率和安全性。 一、设备巡…...

easyui-sidemenu 菜单 后台加载
前言 一个项目的功能较齐全,而齐全就预示着功能菜单比较长,但是现实中在不同的甲方使用中往往只需要摘取其中几项功能,所以就想到用配置菜单以满足其需求,且无需变更原始代码,查找一些资料总是似是而非或是誊抄别的什…...

Python总结上传图片到服务器并保存的两种方式
一、前言 图片保存到服务器的两种方法: 1、根据图片的 URL 将其保存到服务器的固定位置 2、根据 request.FILES.get("file") 方式从请求中获取上传的图片文件,并将其保存到服务器的固定位置 二、方法 1、图片的 URL 要根据图片的 URL 将…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...
