从9.10拼多多笔试第四题产生的01背包感悟
文章目录
- 题面
- 基本的01背包问题
- 本题变式
本文参考:
9.10拼多多笔试ak_牛客网 (nowcoder.com)
拼多多 秋招 2023.09.10 编程题目与题解 (xiaohongshu.com)
题面
拼多多9.10笔试的最后一题,是一道比较好的01背包变式问题,可以学习其解法加深对01背包问题的理解。


这是拼多多2023-9-10秋招笔试的第四题,数据量不大,甚至可以通过dfs暴力穷举写出来,每个部件只有修和换两种选择,总共就是2^N(N<=40)的复杂度,理论上来说这个复杂度是很危险的,但有题友也做出来了。当时自己也是有畏难心理,甚至没有去尝试写dfs,导致这题0分,下次多少得先尝试一下。
可是dfs终究是没那么优雅,这题其实可以巧妙地转换为背包问题。初次尝试时也确实往背包问题考虑了,但是想想一个维度为修车部件N,一个维度为修车时间M,并且题目要求无论是修还是换,这些部件全部都得处理好,也就是物品要被“全部选取”,一般的背包问题好像没法往“全部选择”这上面靠,基本思想都是在有限的容量下达成价值的最大,而选出来物品是“部分选择”出来的。
基本的01背包问题
一个基本的01背包问题如下:
在背包容量为4的情况下,选择价值最大的物品组合。
从打印的答案中也可以看出,最后只选择了15,20这两件物品。
/*** 每件物品只能取一次* @Author jiangxuzhao* @Description* @Date 2023/9/10*/
public class bag01 {public static void main(String[] args) {// 物品价值和成本int[] values = {15, 20, 30};int[] costs = {1, 3, 4};// 背包最多装4int maxBag = 4;// 物品数量int len = costs.length;// dp[i][j]表示从下标为[0,i]物品中选择,放进容量为j的背包中能产生的最大价值// 整体空间根据物品-背包容量排开int[][] dp = new int[len][maxBag+1];// 初始化,这里maxBag+1留下maxBag=0的空间,方便偷懒递归后续背包容量,dp[0][]偷懒指定第一个物品// 倒序初始化保证每个物品只会被选取一次for (int j = maxBag; j>=0; j--){if (j >= costs[0]) {dp[0][j] = dp[0][j-costs[0]] + values[0];}}// 递推公式,本次物品选或者不选for (int i = 1; i < len; i++){// 倒序遍历背包容量保证每个物品只会被选取一次for (int j = maxBag; j>=0; j--){// 不选本次物品idp[i][j] = dp[i-1][j];// 选择本次物品iif (j >= costs[i]) {dp[i][j] = Math.max(dp[i][j], dp[i-1][j-costs[i]]+values[i]);}}}// 结果打印for (int i = 0; i < len; i++){for (int j = 0; j<=maxBag; j++){System.out.print(dp[i][j]+" ");}System.out.println();}}
}
本题变式
提示:这题确实也可以用01背包来做,但是需要经过一层转换。
这里需要求的是在M时间内修好自行车,再去看要的最少金钱,那么首先要检查不计成本,最少时间的情况下是否可以修好自行车,也就是将所有“换部件”的时间累加,判断是否大于M,如果不超过M,则还有降低成本的空间。
假设上面所有“换部件”的累加时间为leastTime,那么M-leastTime就是我们还能够去多花费的缓冲时间,考虑部件i,如果换成“修部件”,在原先的基础上,时间成本增加Ai - Ci,可以减少Di - Bi的成本。这其实就可以转换成01背包问题了,首先在“全部换”的基础上,起码能保证物品能够被“全部选择处理”,然后n个部件中,如果选择“修”,能够多花的总时间容量为M-t,第i个物品修理多花费的时间是Ai-Ci,能减少Di - Bi的成本,求一个“选择处理的修组合”来最大减少成本,保证花钱最少。
最终编码如下:
import java.util.Scanner;/*** 输入样例* 1 10* 10 2 3 5* 输出样例* 2* 输入样例* 1 10* 12 2 3 5* 输出样例* 5* 输入样例* 1 10* 10 2 3 5* 输出样例* 2* @Author jiangxuzhao* @Description* @Date 2023/9/12*/
public class Pdd_9_10_D {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int N = sc.nextInt();int M = sc.nextInt();// 全部换的时间long leastTime = 0L;// 全部换的成本long maxCost = 0L;// 类比01背包,对于物品i,values[i]为可以减少的成本,costs[i]为多花费的时间int[] values = new int[N];int[] costs = new int[N];for(int i = 0; i < N; i++) {// 修时间int Ai = sc.nextInt();// 修成本int Bi = sc.nextInt();// 换时间int Ci = sc.nextInt();// 换成本int Di = sc.nextInt();leastTime += Ci;maxCost += Di;values[i] = Di - Bi;costs[i] = Ai - Ci;}if (leastTime > M){System.out.println(-1);return;}// 最大背包容量 = 多花费的缓冲时间int maxBag = (int)(M - leastTime);// 最大背包价值 = 选择处理的修组合最大减少成本long bagRes = 0L;long[][] dp = new long[N][maxBag+1];// 倒序初始化for(int j = maxBag; j >= 0; j--){if(j >= costs[0]) dp[0][j] = dp[0][j-costs[0]] + values[0];}for (int i = 1; i<N; i++){for (int j = maxBag; j>=0; j--){// 不选当前物品dp[i][j] = dp[i-1][j];// 选当前物品dp[i][j] = Math.max(dp[i][j], dp[i-1][j-costs[i]]+values[i]);}}bagRes = dp[N-1][maxBag];// 最少花费的金钱long res = maxCost - bagRes;System.out.println(res);}
}
相关文章:

从9.10拼多多笔试第四题产生的01背包感悟
文章目录 题面基本的01背包问题本题变式 本文参考: 9.10拼多多笔试ak_牛客网 (nowcoder.com) 拼多多 秋招 2023.09.10 编程题目与题解 (xiaohongshu.com) 题面 拼多多9.10笔试的最后一题,是一道比较好的01背包变式问题,可以学习其解法加深对…...
搭建自己的OCR服务,第一步:选择合适的开源OCR项目
一、OCR是什么? 光学字符识别(Optical Character Recognition, OCR)是指对文本资料的图像文件进行分析识别处理,获取文字及版面信息的过程。 亦即将图像中的文字进行识别,并以文本的形式返回。 二、OCR的基本流程 1…...

【C++】VScode配置C/C++语言环境(简洁易懂版)
目录 一、下载VScode(装好直接跳第五步)二、安装VScode三、VScode设置语言为中文四、VScode切换主题(个人爱好)五、下载C语言编译器(MinGW-W64 GCC)六、配置编译器环境变量七、配置VScode八、使用单独窗口…...

【hive】—原有分区表新增加列(alter table xxx add columns (xxx string) cascade;)
项目场景: 需求:需要在之前上线的分区报表中新增加一列。 实现方案: 1、创建分区测试表并插入测试数据 drop table test_1; create table test_1 (id string, score int, name string ) partitioned by (class string) row format delimit…...
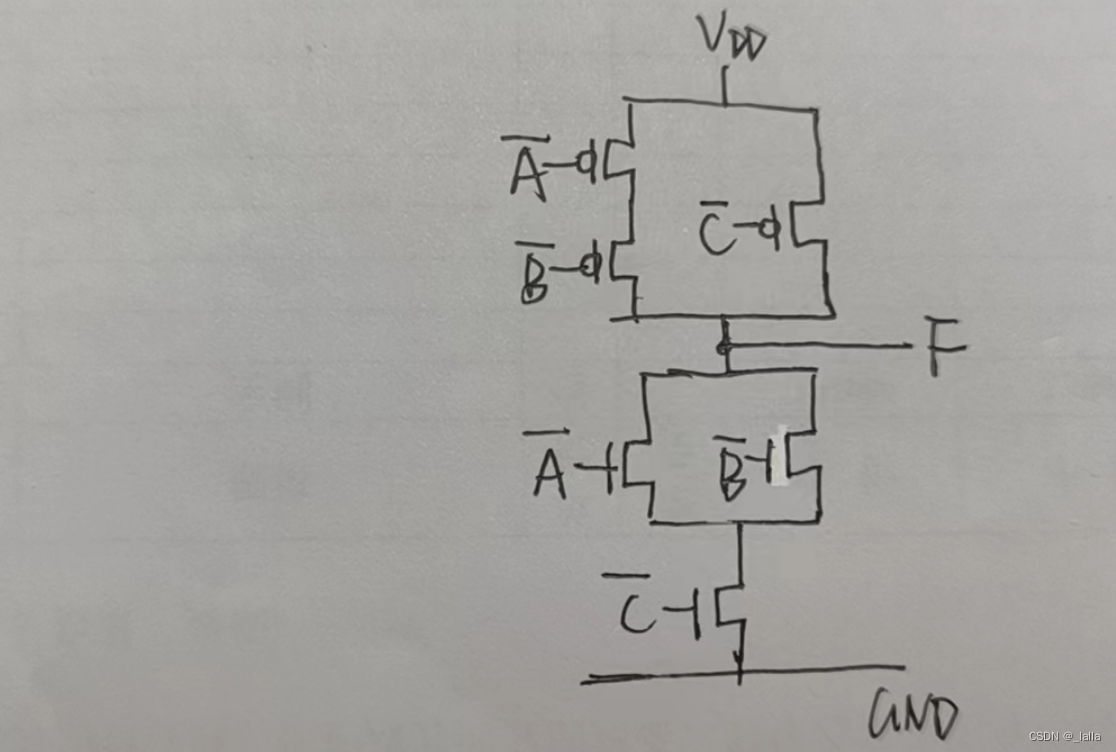
verilog学习笔记7——PMOS和NMOS、TTL电路和CMOS电路
文章目录 前言一、PMOS和NMOS1、NMOS2、PMOS3、增强型和耗尽型4、两者面积大小 二、CMOS门电路1、非门2、与非门3、或非门4、线与逻辑5、CMOS传输门6、三态门 三、TTL电路四、TTL电路 VS CMOS电路五、数字电平六、使用CMOS电路实现逻辑函数1、上拉网络 PUN2、下拉网络 PDN3、实…...

Java知识点二
Java知识点二 1、Comparable内部比较器,Comparator外部比较器2、源码结构的区别:1)Comparable接口:2)Comparator接口: 2、Java反射 1、Comparable内部比较器,Comparator外部比较器 我们一般把Comparable叫…...
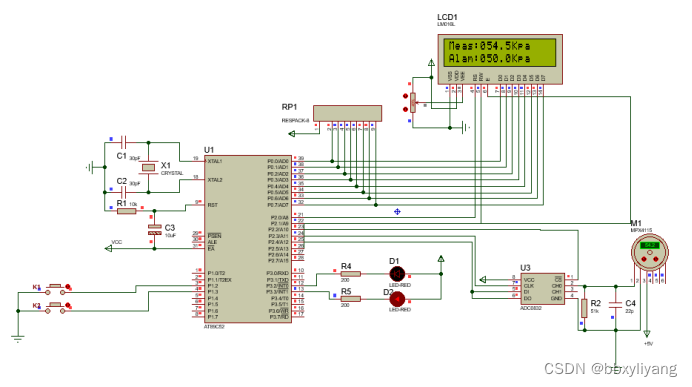
基于单片机压力传感器MPX4115检测-报警系统-proteus仿真-源程序
一、系统方案 本设计采用52单片机作为主控器,液晶1602显示,MPX4115检测压力,按键设置报警,LED报警。 二、硬件设计 原理图如下: 三、单片机软件设计 1、首先是系统初始化 /***************************************…...

Pytorch02 神经网路搭建步骤
文章目录 import numpy as np import torch from PIL.Image import Image from torch.autograd import Variable# 获取数据 def get_data():train_Xnp.asarray([3.3,4.4,5.5,6.71,6.93,4.168,9.779,6.182,7.59,2.167,7.042,10.791,5.313,7.997,5.654,9.27,3.1])train_Ynp.asarr…...
【源码】JavaWeb+Mysql招聘管理系统 课设
简介 用idea和eclipse都可以,数据库是mysql,这是一个Java和mysql做的web系统,用于期末课设作业 cout<<"如果需要的小伙伴可以http://www.codeying.top";可定做课设 线上招聘平台整合了各种就业指导资源,通过了…...
Java中级编程大师班<第一篇:初识数据结构与算法-数组(2)>
数组(Array) 数组是计算机编程中最基本的数据结构之一。它是一个有序的元素集合,每个元素都可以通过索引进行访问。本文将详细介绍数组的特性、用法和注意事项。 数组的基本特性 数组具有以下基本特性: 有序性: 数…...

杰哥教你面试之一百问系列:java集合
文章目录 1. 什么是Java集合?请简要介绍一下集合框架。2. Java集合框架主要分为哪几种类型?3. 什么是迭代器(Iterator)?它的作用是什么?4. ArrayList和LinkedList有什么区别?它们何时适用&#…...

【数据结构】树和二叉树概念
1.树概念及结构 树概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。 有一个特殊的结点,…...
C盘清理教程
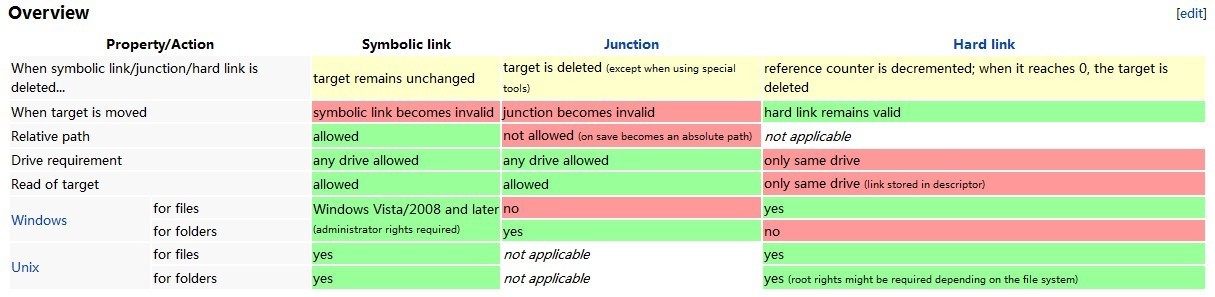
C盘清理教程 首先使用space Sniffer 扫一下c盘,然后看一下到底是哪个文件这么大 第二步,创建软链接。 首先将我们需要移动的文件的当前路径拷贝下来:C:\Users\Tom\Desktop\test-link\abc\ghi.txt 然后假设剪切到D盘下:D:\ghi.…...

【实战-05】 flinksql look up join
摘要 look up join 能做什么? 不饶关子直接说答案, look up join 就是 广播。 重要是事情说三遍,广播。flinksql中的look up join 就类似于flinks flink Datastream api中的广播的概念,但是又不完全相同,对于初次访问…...

C++数据结构--红黑树
目录 一、红黑树的概念二、红黑树的性质三、红黑树的节点的定义四、红黑树结构五、红黑树的插入操作参考代码 五、代码汇总 一、红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过…...

Linux perf使用思考
目录 一、参考资料(建议阅读)二、值得思考的几个问题1、perf使用不同的性能事件进行统计有什么区别呢?2、那使用不同的性能事件统计出来的数据?排序是如何决定的,其中的百分比数值在不同的性能事件进行统计时各自的意义…...

自定义路由断言工厂
我们来设定一个场景: 假设我们的应用仅仅让age在(min,max)之间的人来访问。 第1步:在配置文件中,添加一个Age的断言配置 spring: application:name: api-gateway cloud:nacos:discovery:server-addr: 127.0.0.1:8848gateway:discovery:locator:enabled: trueroute…...
Nacos安装及在项目中的使用
目录 概要一、安装 Nacos1、下载 Nacos2、解压3、启动 Nacos 服务器4、自定义Nacos启动脚本5、访问Nacos Web控制台 二、Nacos----服务注册与发现1、添加 Nacos 依赖2、配置 Nacos 服务器地址3、使用 Nacos 注册服务4、启动服务 三、Nacos----配置管理1、创建配置数据2、从 Nac…...

overleaf中latex语法总结
α和bata $\alpha$ $\beta$上标和下标同时使用 $A_{IJ}^{IJ}$\\ %上标^下标_多个使用{}行内公式 \noindent $abc$\\ %行内公式\documentclass{article} \usepackage[utf8]{inputenc} \usepackage[namelimits]{amsmath} %数学公式 \usepackage{amssymb} %数学公式…...
Grafana配置邮件告警
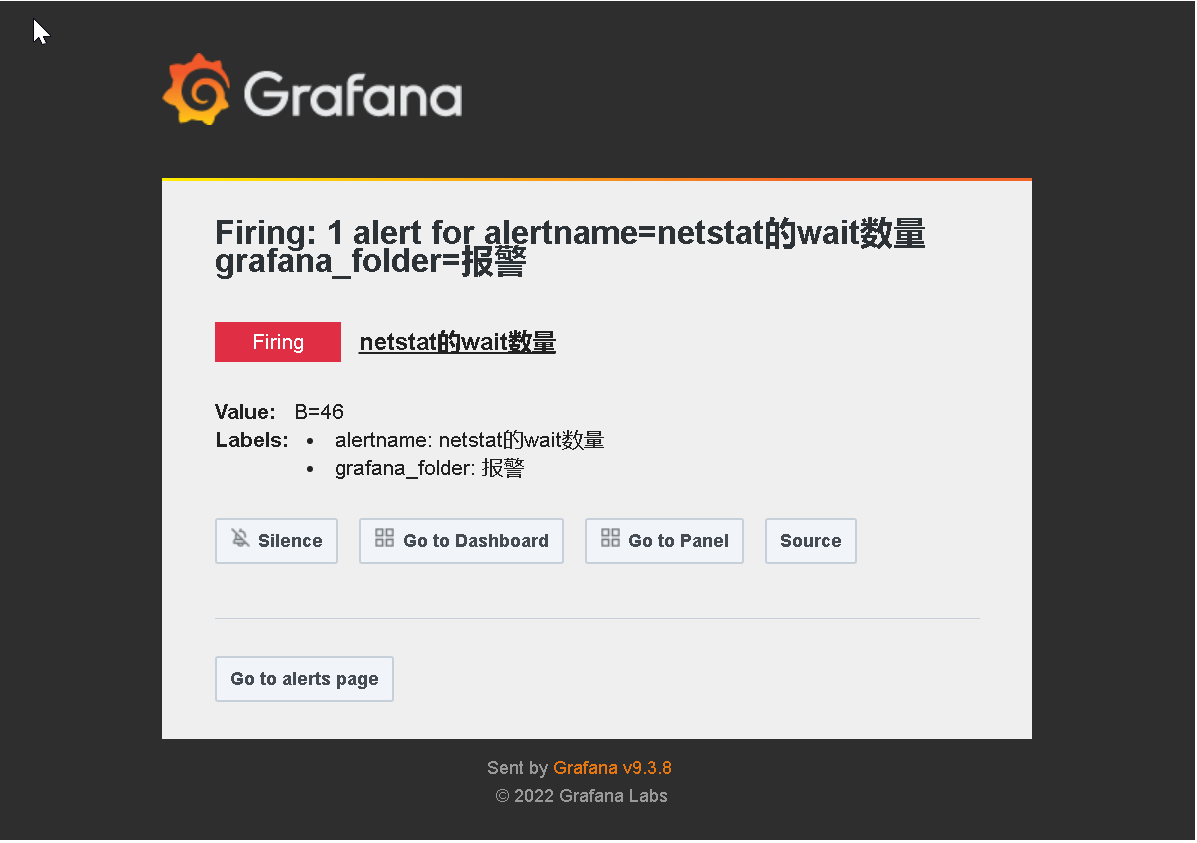
1、创建一个监控图 2、grafana邮件配置 vim /etc/grafana/grafana.ini [smtp] enabled true host smtp.163.com:465 user qinziteng05163.com password xxxxx # 授权码 from_address qinziteng05163.com from_name Grafanasystemctl restart grafana-serv…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...
代理服务器-LVS的3种模式与调度算法
作者介绍:简历上没有一个精通的运维工程师。请点击上方的蓝色《运维小路》关注我,下面的思维导图也是预计更新的内容和当前进度(不定时更新)。 我们上一章介绍了Web服务器,其中以Nginx为主,本章我们来讲解几个代理软件:…...
