——二叉树
二叉树种类
二叉树有两种主要的形式:满二叉树和完全二叉树。
满二叉树
如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。

完全二叉树
在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层(h从1开始),则该层包含 1~ 2^(h-1) 个节点。

堆就是一棵完全二叉树,同时保证父子节点的顺序关系。
二叉搜索树
二叉搜索树是一个有序树。
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树

平衡二叉搜索树
又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。

二叉树的存储方式
二叉树可以链式存储,也可以顺序存储。
那么链式存储方式就用指针, 顺序存储的方式就是用数组。
链式存储
顺序存储

如果父节点的数组下标是 i,那么它的左孩子就是 i * 2 + 1,右孩子就是 i * 2 + 2。
二叉树的遍历方式
二叉树主要有两种遍历方式:
- 深度优先遍历:先往深走,遇到叶子节点再往回走。
- 广度优先遍历:一层一层的去遍历。
前中后,其实指的就是中间节点的遍历顺序
深度优先遍历
前序遍历(递归法,迭代法)
中序遍历(递归法,迭代法)
后序遍历(递归法,迭代法)

广度优先遍历
层次遍历(迭代法)
作者声明
如有问题,欢迎指正!
相关文章:

——二叉树
二叉树种类 二叉树有两种主要的形式:满二叉树和完全二叉树。 满二叉树 如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。 完全二叉树 在完全二叉树中,除了最底层节点可能没…...

【linux命令讲解大全】103.Linux目录堆栈命令 dirs 的使用方法和选项详解
文章目录 dirs概要主要用途选项参数返回值例子注意 从零学 python dirs 显示目录堆栈。 概要 dirs [-clpv] [N] [-N] 主要用途 显示目录堆栈。 清空目录堆栈。 选项 -c:清空目录堆栈。-l:堆栈内以~开头的目录在显示时展开。-p:将目录堆…...
vue3项目应用font awesome6
element-plus框架的图标icon种类较少,一般无法涵盖所有业务情况 这时候引入font awesome6免费版,图标库非常丰富,一般可以满足所有业务场景 官网:https://fa6.dashgame.com/Font Awesome 6,一套始终绝佳的图标字体库…...

【JavaScript】JS语法入门到实战
文章目录 一、初识JavaScript1. 什么是JavaScript?2. JavaScript 和 HTML 和 CSS 之间的关系3. JavaScript的运行过程4. JavaScript的组成 二、JavaScript的书写形式三、变量1. 输入输出2. 变量的使用3. 数据类型 四、运算符五、分支和循环语句1. 分支语句2. 循环语…...
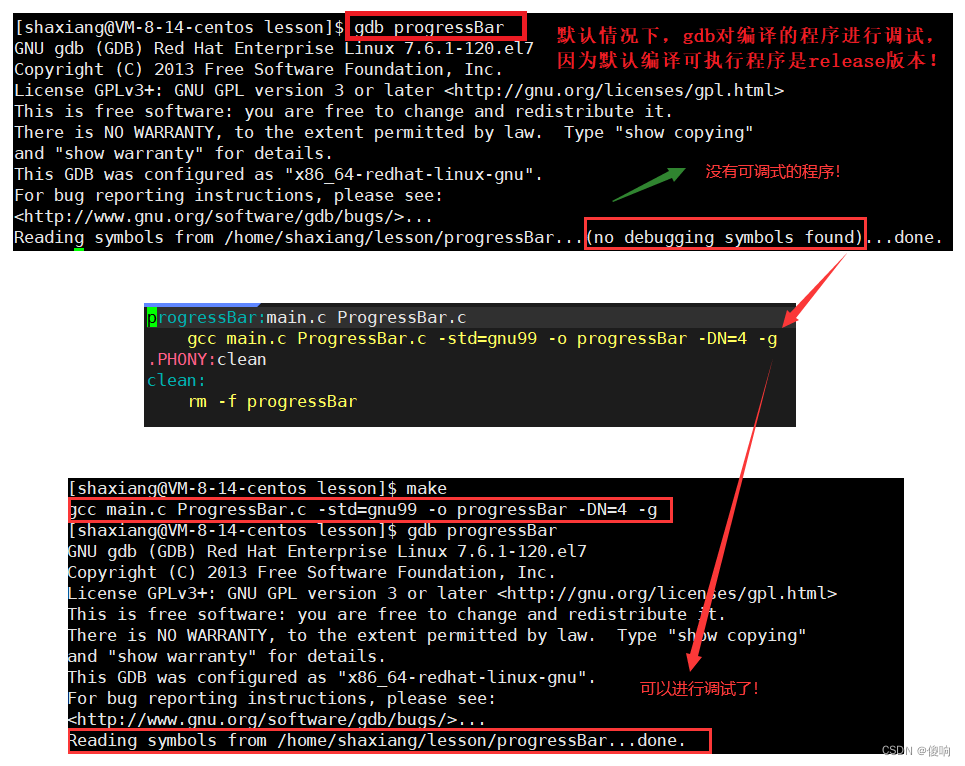
【Linux】工具Gdb调试轻度使用(C++)
目录 一、Gdb背景 二、Gdb基本命令 【2.1】list | l 【2.2】break | b 【2.5】delete | d 【2.6】disable 【2.7】enable 【2.3】info 【2.4】info locals 【2.6】run | r 【2.7】next | n 【2.8】step | s 【2.9】 continue | c 【2.10】bt 【2.11】finish 三…...

linux xhost命令
xhost命令 XHOST 用于管理允许访问系统上 X Server 的主机和用户列表,这些主机和用户都可以从其他主机和同一系统上的其他用户访问。 通常,远程访问将被禁用,因为它会带来安全风险。 但是,如果我们需要在远程计算机上运行 GUI &…...

linux在线源码阅读网站
下面的网站可以在线阅读linux源码,提供了类似github上分析工具,自动具备符号关联的作用,可以方便的供用户分析代码。除了可以分析linux源码外,该网站还可以分析一些其它源码,例如qt等 这个网站有许多功能,…...

css中只使用vue的变量
参考:https://blog.csdn.net/FellAsleep/article/details/130617163 1、必须作用在用一个div上 2、变量必须有双横杠“–” <spanclass"bb" :style"spanStyle">11</span>data() {return {spanStyle: {"--color": #bfa /…...
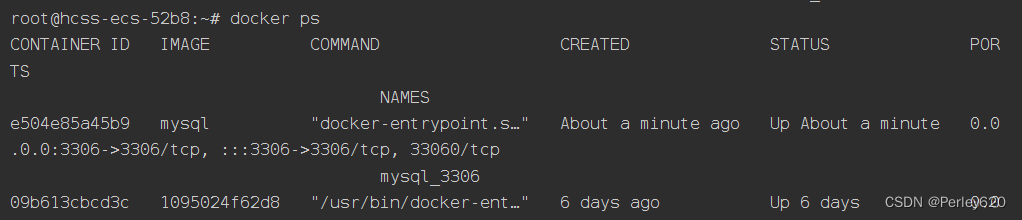
华为云云耀云服务器L实例评测 | 由于自己原因导致MySQL数据库被攻击 【更新中。。。】
目录 引出起因(si因)解决报错诶嘿,连上了 不出意外,就出意外了打开数据库what??? 找华为云求助教训:备份教训:密码 解决1.改密码2.新建一个MySQL,密码设置复杂…...

如何查询成绩或工资
为什么每次查询成绩或者工资的时候都觉得麻烦又耗时呢?在过去,我们可能需要去学校或公司的相关部门,填写繁琐的表格,然后等待工作人员进行查询和处理。这不仅浪费了我们宝贵的时间,还可能出现查询结果不准确或者遗漏的…...

FPGA原理与结构——时钟IP核的使用与测试
一、前言 本文介绍xilinx的时钟IP核 Clocking Wizard v6.0的具体使用与测试过程,在学习一个IP核的使用之前,首先需要对于IP核的具体参数和原理有一个基本的了解,具体可以参考: FPGA原理与结构——时钟IP核原理学习https://blog.c…...
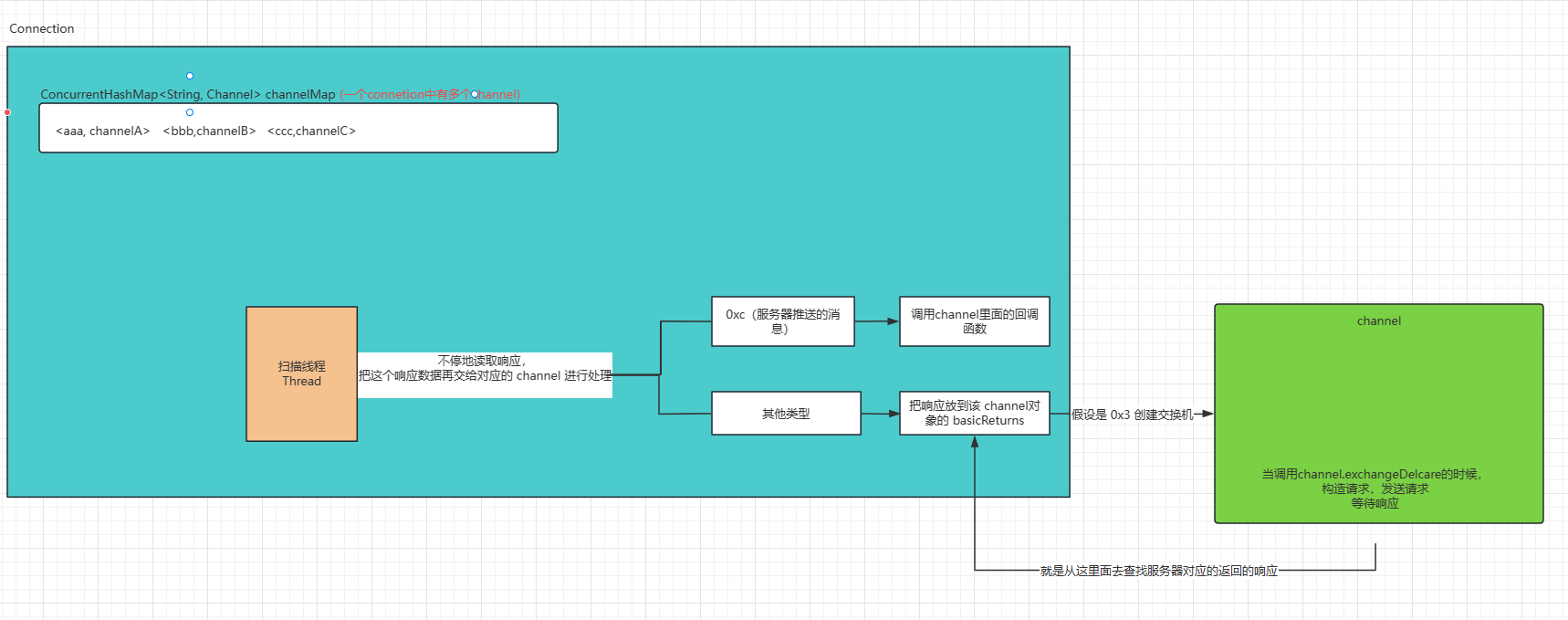
手搓消息队列【RabbitMQ版】
什么是消息队列? 阻塞队列(Blocking Queue)-> 生产者消费者模型 (是在一个进程内)所谓的消息队列,就是把阻塞队列这样的数据结构,单独提取成了一个程序,进行独立部署~ --------&…...
Oracle VM VirtualBox 安装 Ubuntu Linux
Virtual Box VirtualBox是一个强大的、面向个人用户或者企业用户的虚拟机产品,其支持x86以及AMD64/Intel64的计算架构,功能特性丰富、性能强劲,支持GPL开源协议,其官方网址是www.virtualbox.org,由Oracle开源…...
3D WEB轻量化引擎HOOPS Commuicator技术概览(一):数据导入与加载
HOOPS Communicator是一款功能强大的SDK,适用于基于Web的高级工程应用程序,代表HOOPS Web平台的Web开发组件。使用HOOPS Communicator,您可以构建一个在 Web浏览器中提供3D模型的Web应用程序。 HOOPS Communicator可以本地加载多种模型格式。…...
.net 7 隐藏swagger的api
1.写一个隐藏接口特性表示 using Microsoft.AspNetCore.Mvc.ApiExplorer; using Microsoft.OpenApi.Models; using Swashbuckle.AspNetCore.SwaggerGen;using System.Web.Http.Description;namespace JiaTongInterface.Filter {public class SwaggerApi : Swashbuckle.AspNet…...

Maven插件的作用
插件-maven-compiler-plugin <plugin> <groupId>org.apache.maven.plugins</groupId> <artifactId>maven-compiler-plugin</artifactId> <configuration> <sourc…...

C++(三)——运算符重载
运算符重载 重定义或重载大部分 C 内置的运算符就能使用自定义类型的运算符。重载的运算符是带有特殊名称的函数,函数名是由关键字 operator 和其后要重载的运算符符号构成的。与其他函数一样,重载运算符有一个返回类型和一个参数列表。不能为了重载而重…...
【Springcloud】elk分布式日志
【Springcloud】elk分布式日志 【一】基本介绍【二】Elasticsearch【1】简介【2】下载【3】安装【4】启动 【三】Logstash【1】简介【2】下载【3】安装【4】启动 【四】Kibana【1】简介【2】下载【3】安装【4】启动 【五】切换中文【六】日志收集 【一】基本介绍 (…...

面试半个月后的一些想法
源于半个月面试经历后的一些想法,刚开始想的是随便写写,没想到居然写了这么多。 找不到目标找不到意义亦或是烦躁的时候,就写写文章吧,把那些困扰你很久的问题铺开来 花时间仔细想想,其实真正让我们生气懊恼࿰…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...