数据结构——二叉树线索化遍历(前中后序遍历)
二叉树线索化
线索化概念:
为什么要转换为线索化
二叉树线索化是一种将普通二叉树转换为具有特殊线索(指向前驱和后继节点)的二叉树的过程。这种线索化的目的是为了提高对二叉树的遍历效率,特别是在不使用递归或栈的情况下进行遍历。
将二叉树线索化的主要目的是为了提高对二叉树的遍历效率以及节省存储空间。线索化使得在不使用递归或栈的情况下可以更快速地进行遍历,特别是在特定顺序的遍历时,如前序、中序或后序遍历。
提高遍历效率:线索化后,可以在常量时间内找到节点的前驱和后继节点,从而实现更高效的遍历。这对于需要频繁遍历大型二叉树或需要在树的中间部分执行插入和删除操作时特别有用。
无需递归或栈:线索化的二叉树允许你在遍历时省去递归或栈的开销,因为你可以沿着线索直接访问节点的前驱和后继,从而降低了内存和时间复杂度。
节省存储空间:线索化可以用较少的额外存储空间来实现。通常,只需为每个节点添加一个或两个指针来存储线索信息,而不需要额外的数据结构(如堆栈)来辅助遍历。
支持双向遍历:线索化的二叉树可以支持双向遍历,即可以在给定节点的前向和后向方向上遍历树。这在某些应用中很有用,例如双向链表的操作。
节省计算资源:在某些特定的应用场景中,通过线索化可以避免重复计算,因为可以直接访问前驱和后继节点,而无需再次搜索或遍历
树的遍历
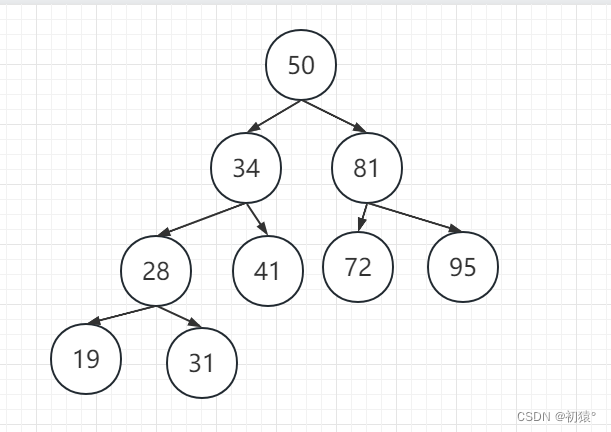
先给定一棵树,然后对他进行每种遍历:
前序遍历:
前序遍历,就是先遍历根节点在遍历左子树,在遍历右子树;
他的顺序就是:根节点->左子树->右子树
根据递归先遍历了根节点,然后递归左子树,回溯后在进行遍历右子树的一个过程;
例如上图开始前序遍历:
遍历根节点50,然后递归左子树,34,现在把34看为根节点继续递归左子树,28,然后把28看作根节点,继续遍历左子树,19,然后把19看为根节点继续遍历,然后左子树为空,开始回溯,回溯到19,遍历右子树也为空,继续回溯到结点28,遍历右子树,31;然后通过这种思想一直进行遍历最总遍历完整棵子树;
前序遍历结果:50,34,28,19,31,41,81,72,95
中序遍历:
顺序是:左子树->根节点->右子树
其实在理解了前序遍历后,中序遍历也差不多的,刚才是先记录了根节点,现在开始,先一直递归遍历左子树,递归到没有左子树的时开始记录,比如上图递归到19,然后回溯,28,遍历右子树31,回溯34,遍历右子树41,回溯50,遍历右子树;然后最终的结果就是:
19,28,31,34,41,50,72,81,95;
中序遍历就是,找到子树的最左边的那个结点,然后回溯到它的父节点,然后遍历他父节点的右子树,然后到右子树中又去找它的最左的结点,这样一直经过这样的操作,最终完成中序遍历。
后序遍历:
顺序是:左子树->右子树->根节点
先是左子树,那就先找到左子树中的最左边的结点,19,然后回溯,遍历右子树,然后再右子树中找最左边的结点,31,回溯28,然后在回溯;这样的一个过程;
最终结果就是:
19,31,28,41,34,72,95,81,50
后序遍历,看着比中序和后序遍历难理解,其实只要懂得了递归回溯的那个过程,就思路回非常的清晰;然后大概的过程就是先遍历左子树,找到左子树中最左边的结点,回溯,然后遍历右子树,遍历右子树的过程也是先遍历右子树中的左子树,然后再进行遍历右子树的右子树,最后来遍历他们的根节点;
3种遍历的代码实现:
void pre_orderNode(Node *root) {前序if (!root) return ;printf("%d ", root->data);//先输出根节点pre_orderNode(root->lchild);//遍历左子树pre_orderNode(root->rchild);//遍历右子树return ; }void in_orderNode(Node *root) {中序if (!root) return ;in_orderNode(root->lchild);//先遍历左子树printf("%d ", root->data);//在打印根节点的值in_orderNode(root->rchild);//在遍历右子树return ; }void post_orderNode(Node *root) {后序if (!root) return ;post_orderNode(root->lchild);//先遍历左子树post_orderNode(root->rchild);//在遍历右子树printf("%d ", root->data);//最终打印根节点值return ; }可以去理解一下代码,尝试在纸上或者脑子里执行以下代码,模拟运行以下;
二叉树前序线索化:
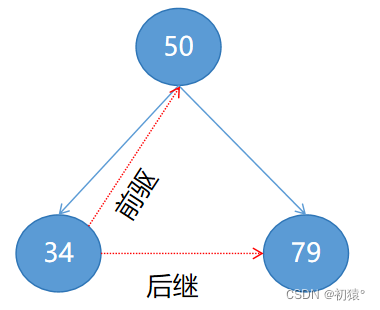
如图上图一个简单的二叉树,现在是将这个二叉树进行前序线索化,那么前序遍历的顺序是根节点->左子树->右子树;
那么根节点就应该在条线的头部,然后再去遍历左子树和右子树,那么这个数的前序遍历结果是50,34,79;
那么就可以将二叉树样来看,50是34的前驱,79是34的后继,前驱就是在遍历在他前面的,后继就是在他后面遍历的;
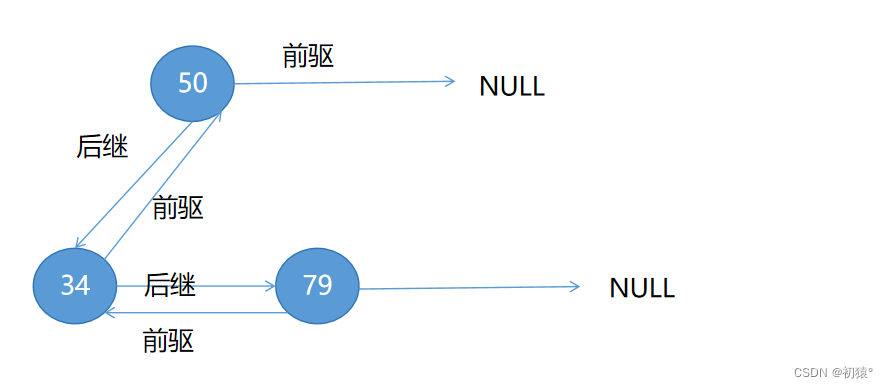
现在我们将每个结点的指向两个子孩子指针改变为指向他的前驱和后继:
通过这样的转换,那这棵树就转换为一条双向链表了:
其中会发下50和79的会右一颗子树指向NULL,那么就需要用一个变量来记录,他是否右前驱或者后继;
就是这样的一个转换,也证明了概念种的节省空间,不用递归遍历,可以双向遍历,提高了遍历效率;
下面是代码实现:
#include <stdio.h> #include <stdlib.h> #include <time.h>#define NORMAL 0 #define THRENA 1 //这里左儿子记录前驱,右儿子记录后继 typedef struct Node {int val, ltag, rtag;//val结点的值,ltag记录是否有前驱,rtag记录是否有后继struct Node *lchild, *rchild; } Node;Node *getNewNode(int val) {//获取新的结点Node *root = (Node *)malloc(sizeof(Node));root->lchild = root->rchild = NULL;root->rtag = root->ltag = NORMAL;//NORMAL表示还未有前驱或后继root->val = val;return root; }Node *insert(Node *root, int val) {//添加结点,组成普通的二叉树if (!root) return getNewNode(val);if (root->val == val) return root;if (root->val > val) root->lchild = insert(root->lchild, val);else root->rchild = insert(root->rchild, val);return root; }void build_Thread(Node *root) {//建立线索化if (!root) return ; static Node *pre = NULL;//使用静态变量使得pre值不随程序递归而改变Node *left = root->lchild;//记录当前结点左右儿子 Node *right = root->rchild;if (root->ltag == NORMAL) {//当前结点没有前驱结点root->lchild = pre;//给当前结点赋值前驱结点root->ltag = THRENA;//标记有前驱结点}if (pre && pre->rtag == NORMAL) {//如果它的前驱结点没有后继,并且前驱结点不为NULLpre->rchild = root;//将前驱结点的后继附上当前结点pre->rtag = THRENA;//标记前驱结点有后继了}pre = root;//pre等于当前递归的结点build_Thread(left);//递归左子树build_Thread(right);//在递归右子树return ; }void output(Node *root) {//遍历线索化二叉树if (!root) return ;Node *p = root;while (p) {printf("%d ", p->val);if (p->rtag == THRENA) p = p->rchild;//说明当前结点有后继直接往右节点也就是后继结点继续遍历else if (p->rtag == NORMAL) break;//如果当前结点没有后继结束遍历 }return ; }void preface(Node *root) {//普通前序递归遍历if (!root) return ;printf("%d ", root->val);if (root->ltag == NORMAL) preface(root->lchild);if (root->rtag == NORMAL) preface(root->rchild);return ; }void clearNode(Node *root) {//回收空间if (!root) return ;if (root->ltag == NORMAL) clearNode(root->lchild);if (root->rtag == NORMAL) clearNode(root->rchild);free(root);return ; }int main() {srand(time(0));//获取当期计算时间,获取随机数Node *root = NULL;for (int i = 0; i < 10; i++) {int val = rand() % 100;root = insert(root, val);}preface(root);//先打印普通前序遍历putchar(10);//换行build_Thread(root);//建立线索化output(root);//输出前序线索化putchar(10);clearNode(root);return 0; }二叉树中序线索化:
中序遍历顺序:左子树->根节点->右子树
那么结果借是34,50,79
转换线索化,那么34就是50的前驱,50就是34的后继;和前序遍历的是一样的;
直接来看代码实现:
#include <stdio.h> #include <stdlib.h> #include <time.h> #define NORMAL 0 //表示没有 #define THRENA 1 //表示有 //这里左儿子记录前驱,右儿子记录后继 typedef struct Node {int val, ltag, rtag;///val结点的值,ltag记录是否有前驱,rtag记录是否有后继struct Node *lchild, *rchild; } Node;Node *getNewNode(int val) {///获取新的结点Node *p = (Node *)malloc(sizeof(Node));p->val = val;p->lchild = p->rchild = NULL;p->ltag = p->rtag = NORMAL;//NORMAL表示还未有前驱或后继return p; }Node *insert(Node *root, int val) {//添加结点,组成普通的二叉树if (!root) return getNewNode(val);if (root->val == val) return root;if (root->val > val) root->lchild = insert(root->lchild, val);else root->rchild = insert(root->rchild, val);return root; }void in_order(Node *root) {//普通递归中序遍历if (!root) return ;if (root->ltag == NORMAL) in_order(root->lchild);printf("%d ", root->val);if (root->rtag == NORMAL) in_order(root->rchild);return ; }void build_Thread(Node *root) {//建立线索化if (!root) return ;static Node *pre = NULL;//使用静态变量使得pre值不随函数递归过程改变而改变build_Thread(root->lchild);//由于是中序遍历,先递归到最左结点//中间过程就是想当于根节点if (root->ltag = NORMAL) {root->lchild = pre;root->ltag = THRENA;}if (pre && pre->rchild == NORMAL) {pre->rchild = root; pre->rtag = THRENA;}pre = root;build_Thread(root->rchild);//然后再遍历右子树return ; }Node *most_left(Node *root) {//找到最左结点Node *temp = root;while (temp && temp->ltag == NORMAL && temp->lchild != NULL) temp = temp->lchild;return temp; }void output(Node *root) {if (!root) ;Node *p = most_left(root);//从最左结点开始遍历while (p) {printf("%d ", p->val);if (p->rtag == THRENA) p = p->rchild;//如果后继存在进行遍历后继else p = most_left(p->rchild);//找到右子树的最左结点继续遍历}return ; }void clear(Node *root) {if (!root) return ;if (root->ltag == NORMAL) clear(root->lchild);if (root->rtag == NORMAL) clear(root->rchild);free(root);return ; }int main() {srand(time(0)); Node *root = NULL;for (int i = 0; i < 10; i++) {int val = rand() % 100;root = insert(root, val);}in_order(root);putchar(10);build_Thread(root);output(root);putchar(10);clear(root);return 0; }二叉树后序线索化:
直接上代码演示,如果前面两种你都弄懂了那么,后序理解起来也非常容易:
#include <stdio.h> #include <stdlib.h> #include <time.h>#define NORMAL 0 #define THRENA 1 typedef struct Node {int val, ltag, rtag;struct Node *lchild, *rchild; } Node;Node *getNewNode(int val) {Node *root = (Node *)malloc(sizeof(Node));root->lchild = root->rchild = NULL;root->rtag = root->ltag = NORMAL;root->val = val;return root; }Node *insert(Node *root, int val) {if (!root) return getNewNode(val);if (root->val == val) return root;if (root->val > val) root->lchild = insert(root->lchild, val);else root->rchild = insert(root->rchild, val);return root; }void build_Thread(Node *root) {if (!root) return ; static Node *pre = NULL;build_Thread(root->lchild);build_Thread(root->rchild);if (root->ltag == NORMAL) {root->lchild = pre;root->ltag = THRENA;}if (pre && root->rtag == NORMAL) {pre->rchild = root;pre->rtag = THRENA;}pre = root;return ; }Node *most_left(Node *root) {while (root && root->ltag == THRENA && root->lchild) root = root->lchild;return root; }void output(Node *root) {if (!root) return ;Node *p = most_left(root);while (p) {printf("%d ", p->val);if (p->rtag == THRENA) p = p->rchild; else if (p->rtag == NORMAL) break;}return ; }void back_order(Node *root) {if (!root) return ;if (root->ltag == NORMAL) back_order(root->lchild);if (root->rtag == NORMAL) back_order(root->rchild);printf("%d ", root->val);return ; }void preface(Node *root) {if (!root) return ;printf("%d(", root->val);if (root->ltag == NORMAL) preface(root->lchild);printf(",");if (root->rtag == NORMAL) preface(root->rchild);printf(")");return ; }void clearNode(Node *root) {if (!root) return ;if (root->ltag == NORMAL) clearNode(root->lchild);if (root->rtag == NORMAL) clearNode(root->rchild);free(root);return ; }int main() {srand(time(0)); Node *root = NULL;for (int i = 0; i < 10; i++) {int val = rand() % 100;root = insert(root, val);}preface(root);putchar(10);back_order(root);putchar(10);build_Thread(root);output(root);putchar(10);clearNode(root);return 0; }
相关文章:
数据结构——二叉树线索化遍历(前中后序遍历)
二叉树线索化 线索化概念: 为什么要转换为线索化 二叉树线索化是一种将普通二叉树转换为具有特殊线索(指向前驱和后继节点)的二叉树的过程。这种线索化的目的是为了提高对二叉树的遍历效率,特别是在不使用递归或栈的情况下进行遍历…...
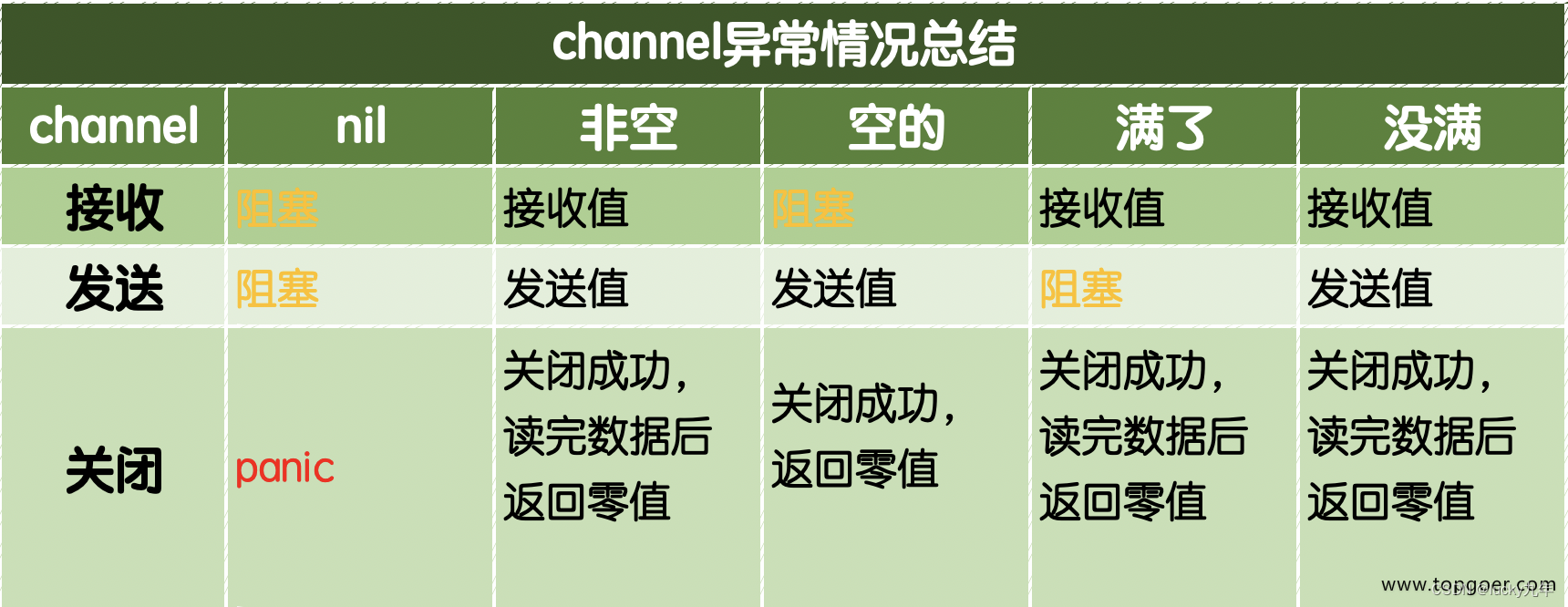
GO语言网络编程(并发编程)Channel
GO语言网络编程(并发编程)Channel 1、Channel 1.1.1 Channel 单纯地将函数并发执行是没有意义的。函数与函数间需要交换数据才能体现并发执行函数的意义。 虽然可以使用共享内存进行数据交换,但是共享内存在不同的goroutine中容易发生竞态…...

c++day3
stack.h #ifndef STACK_H #define STACK_H #include <iostream> //#define max 128 using namespace std; class Stack { private:int* stack;//数组指针int top;//栈顶元素int max;//栈容量 public://构造函数Stack();//析构函数~Stack();//定义拷贝构造函数Stack(cons…...
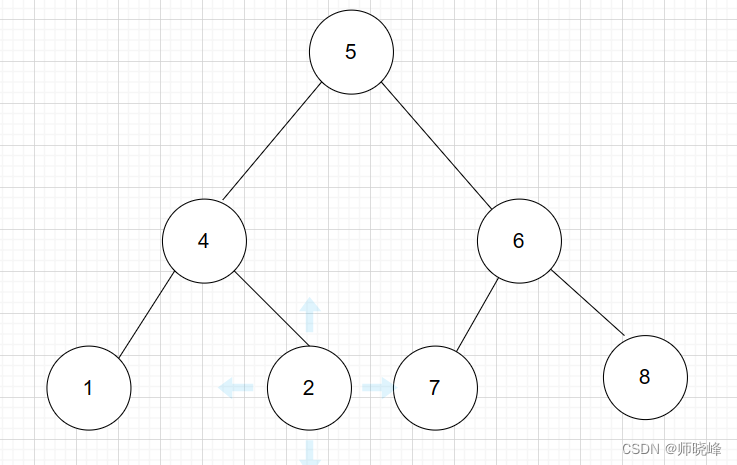
算法通过村第六关-树青铜笔记|中序后序
文章目录 前言1. 树的常见概念2. 树的性质3. 树的定义与存储方式4. 树的遍历方式5. 通过序列构建二叉树5.1 前中序列恢复二叉树5.2 中后序列恢复二叉树 总结 前言 提示:瑞秋是个小甜心,她只喜欢被爱,不懂的去爱人。 --几米《你们 我们 他们》…...

C++动态内存管理+模板
💓博主个人主页:不是笨小孩👀 ⏩专栏分类:数据结构与算法👀 C👀 刷题专栏👀 C语言👀 🚚代码仓库:笨小孩的代码库👀 ⏩社区:不是笨小孩👀 🌹欢迎大…...
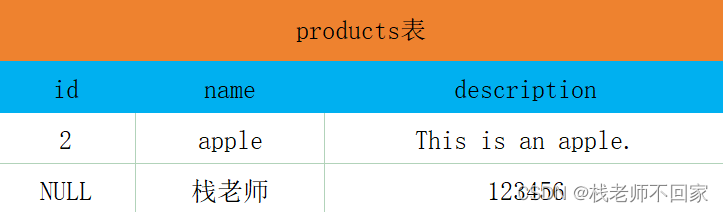
SQL 注入漏洞攻击
文章目录 1. 介绍2. 无密码登录3. 无用户名无密码登录4. 合并表获取用户名密码 1. 介绍 假设你用自己的用户名和密码登录了一个付费网站,网站服务器就会查询一下你是不是 VIP 用户,而用户数据都是放在数据库中的,服务器通常都会向数据库进行查…...

一篇五分生信临床模型预测文章代码复现——Figure 10.机制及肿瘤免疫浸润(四)
之前讲过临床模型预测的专栏,但那只是基础版本,下面我们以自噬相关基因为例子,模仿一篇五分文章,将图和代码复现出来,学会本专栏课程,可以具备发一篇五分左右文章的水平: 本专栏目录如下: Figure 1:差异表达基因及预后基因筛选(图片仅供参考) Figure 2. 生存分析,…...

Transformer 模型中常见的特殊符号
Transformer 模型中常见的特殊符号 通过代码一起理解一下 Transformer 模型中常见的特殊符号, 示例代码, special_tokens{unk_token: [UNK], sep_token: [SEP], pad_token: [PAD], cls_token: [CLS], mask_token: [MASK]}这段代码是定义了一个字典spec…...

C# halcon SubImage的使用
SubImage(HObject imageMinuend, HObject imageSubtrahend, out HObject imageSub, HTuple mult, HTuple add) 公式 x1imageMinuend此行此列的灰度 x2imageSubtrahend此行此列的灰度 则imageSub此行此列的灰度为;(x1-x2)*multadd 溢出裁剪 以byte图为例,小于0&a…...
)
每天几道Java面试题:异常机制(第三天)
目录 第三幕、第一场)异常机制面试题 友情提醒 背面试题很枯燥,加入一些戏剧场景故事人物来加深记忆。PS:点击文章目录可直接跳转到文章指定位置。 第三幕、 第一场)异常机制面试题 【面试官老吉,面试官潘安,面试者…...

Linux 中的 chattr 命令及示例
Linux 中的chattr命令是一个文件系统命令,用于更改目录中文件的属性。该命令的主要用途是使多个文件无法被超级用户以外的用户更改。管理员表示,众所周知,Linux 是一个多用户操作系统,一个用户有可能删除另一个用户非常关心的文件。为了避免这种情况,Linux 提供了“ chatt…...

LeetCode 2605. Form Smallest Number From Two Digit Arrays【数组,哈希表,枚举;位运算】1241
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

VoxWeekly|The Sandbox 生态周报|20230904
欢迎来到由 The Sandbox 发布的《VoxWeekly》。我们会在每周发布,对上一周 The Sandbox 生态系统所发生的事情进行总结。 如果你喜欢我们内容,欢迎与朋友和家人分享。请订阅我们的 Medium 、关注我们的 Twitter,并加入 Discord 社区…...

antd setFieldsValue 设置初始值无效AutoComplete 设置默认值失败
antd form setFieldsValue 设置初始值无效 解决方案 setTimeout(()>{setFieldsValue(values)},100)antd AutoComplete 设置默认值失败 defaultValue 设置无效 解决方案 设置value,搭配onChange来设置修改...

01-Redis核心数据结构与高性能原理
上一篇: 1.Redis安装 下载地址:http://redis.io/download 安装步骤: # 安装gcc yum install gcc# 把下载好的redis-5.0.3.tar.gz放在/usr/local文件夹下,并解压 wget http://download.redis.io/releases/redis-5.0.3.tar.gz…...

预防Dos攻击
Dos----拒绝服务攻击,一般是构造特殊的输入,使得后台的处理耗时远超正常水平,随着请求越来越多,后台服务越发疲于奔命,最后因资源耗尽,无法再接受新的请求,最终造成拒绝服务的效果。 特殊输入例…...

ant design的文档真的是一坨屎
很多基础设置 高傲的写都不写 要自己去index.d.ts里查 这就算了,为什么还有错的。。。。。 即使因为版本号而不同,起码把差异说明一下吧,直接丢个错的什么意思,。。。。。。。。 没点子功夫还真用不了 文档 进度条 Progress -…...

关于迁移学习的一点理解
举个栗子,老虎图片的数量非常少,可以让网络先学会识别猫的图片 1、预训练模型 内容:利用在 ImageNet1000 数据集训练好的模型,将所需的模型参数下载,嵌入到对应的网络架构中,使用对预训练模型的搭建。目前P…...
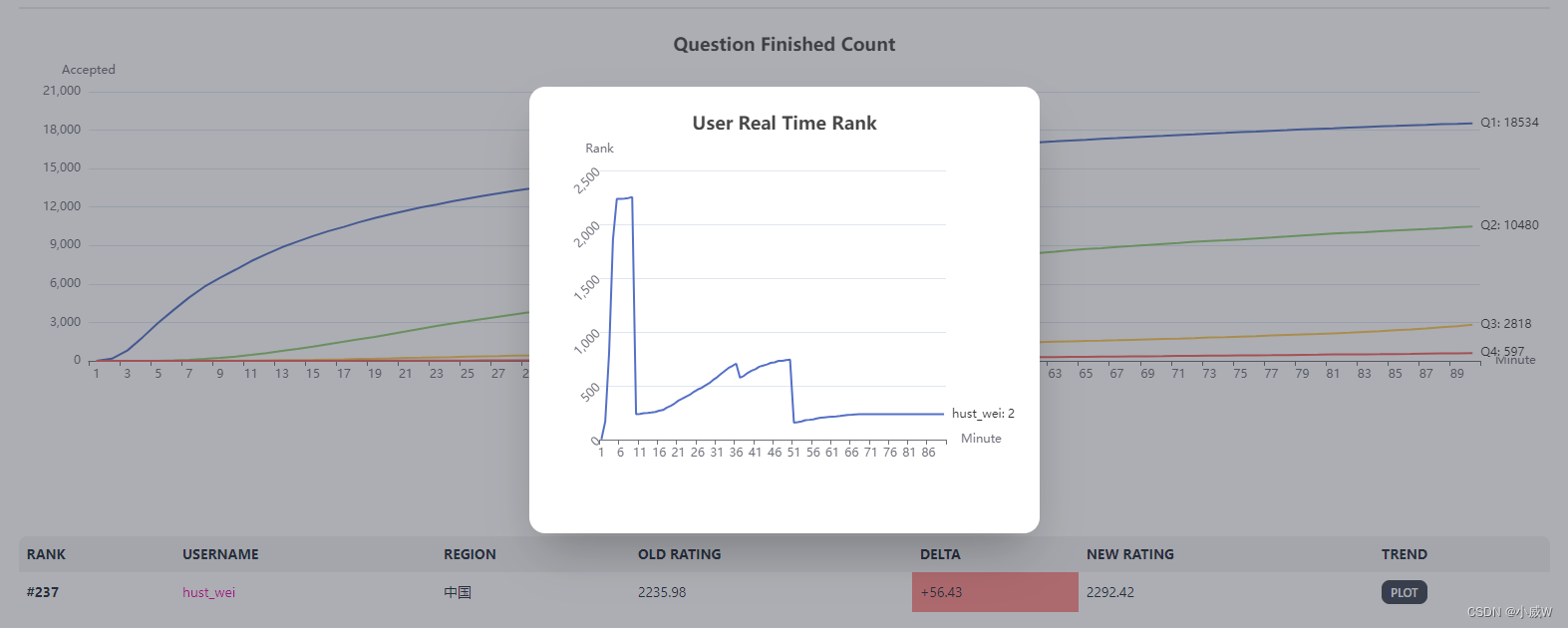
【力扣周赛】第 361 场周赛(⭐前缀和+哈希表 树上倍增、LCA⭐)
文章目录 竞赛链接Q1:7020. 统计对称整数的数目竞赛时代码——枚举预处理 Q2:8040. 生成特殊数字的最少操作(倒序遍历、贪心)竞赛时代码——检查0、00、25、50、75 Q3:2845. 统计趣味子数组的数目竞赛时代码——前缀和…...
解决 Android 依赖冲突
解决办法 问题原因就是,各个模块所有的依赖(递归)的 jar 包最后都会加载到安卓的项目中,你可以选择 project 形式查看 External Libraries,都在这了。所以解决问题关键就是干掉冲突,剩下一个就行了…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...