算法训练营day49|动态规划 part10:(LeetCode 121. 买卖股票的最佳时机、122.买卖股票的最佳时机II)
121. 买卖股票的最佳时机
题目链接🔥
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0
贪心方法
取最左最小值,取最右最大值,那么得到的差值就是最大利润。
class Solution {
public:int maxProfit(vector<int>& prices) {int low = INT_MAX;int result = 0;for (int i = 0; i < prices.size(); i++) {low = min(low, prices[i]); // 取最左最小价格result = max(result, prices[i] - low); // 直接取最大区间利润}return result;}
}
动规方法
- 确定dp数组(dp table)以及下标的含义
dp[i][0] 表示第i天持有股票所得最多现金 ,这里可能有同学疑惑,本题中只能买卖一次,持有股票之后哪还有现金呢?
其实一开始现金是0,那么加入第i天买入股票现金就是 -prices[i], 这是一个负数。
dp[i][1] 表示第i天不持有股票所得最多现金
注意这里说的是“持有”,“持有”不代表就是当天“买入”!也有可能是昨天就买入了,今天保持持有的状态
很多同学把“持有”和“买入”没区分清楚。
在下面递推公式分析中,我会进一步讲解。
- 确定递推公式
如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
- 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][0]
- 第i天买入股票,所得现金就是买入今天的股票后所得现金即:-prices[i]
那么dp[i][0]应该选所得现金最大的,所以dp[i][0] = max(dp[i - 1][0], -prices[i]);
如果第i天不持有股票即dp[i][1], 也可以由两个状态推出来
- 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1][1]
- 第i天卖出股票,所得现金就是按照今天股票价格卖出后所得现金即:prices[i] + dp[i - 1][0]
同样dp[i][1]取最大的,dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
这样递推公式我们就分析完了
- dp数组如何初始化
由递推公式 dp[i][0] = max(dp[i - 1][0], -prices[i]); 和 dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);可以看出
其基础都是要从dp[0][0]和dp[0][1]推导出来。
那么dp[0][0]表示第0天持有股票,此时的持有股票就一定是买入股票了,因为不可能有前一天推出来,所以dp[0][0] -= prices[0];
dp[0][1]表示第0天不持有股票,不持有股票那么现金就是0,所以dp[0][1] = 0;
- 确定遍历顺序
从递推公式可以看出dp[i]都是由dp[i - 1]推导出来的,那么一定是从前向后遍历。
- 举例推导dp数组

dp[5][1]就是最终结果。
代码实现
class Solution {
public:int maxProfit(vector<int>& prices) {vector<vector<int>> dp(prices.size(),vector<int> (2));dp[0][0]=-prices[0];for(int i=1;i<prices.size();i++){dp[i][0]=max(-prices[i],dp[i-1][0]);dp[i][1]=max(dp[i-1][0]+prices[i],dp[i-1][1]);}return dp[prices.size()-1][1];}
};
122.买卖股票的最佳时机II
题目链接🔥🔥
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 3 * 10 ^ 4
0 <= prices[i] <= 10 ^ 4
思路分析
本题和121. 买卖股票的最佳时机 的唯一区别是本题股票可以买卖多次了(注意只有一只股票,所以再次购买前要出售掉之前的股票)
在动规五部曲中,这个区别主要是体现在递推公式上,其他都和121. 买卖股票的最佳时机一样。
所以我们重点讲一讲递推公式。
这里重申一下dp数组的含义:
- dp[i][0] 表示第i天持有股票所得现金。
- dp[i][1] 表示第i天不持有股票所得最多现金
如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
- 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][0]
- 第i天买入股票,所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即:dp[i - 1][1] - prices[i]
注意这里和121. 买卖股票的最佳时机唯一不同的地方,就是推导dp[i][0]的时候,第i天买入股票的情况。
在121. 买卖股票的最佳时机中,因为股票全程只能买卖一次,所以如果买入股票,那么第i天持有股票即dp[i][0]一定就是 -prices[i]。
而本题,因为一只股票可以买卖多次,所以当第i天买入股票的时候,所持有的现金可能有之前买卖过的利润。
那么第i天持有股票即dp[i][0],如果是第i天买入股票,所得现金就是昨天不持有股票的所得现金 减去 今天的股票价格 即:dp[i - 1][1] - prices[i]。
再来看看如果第i天不持有股票即dp[i][1]的情况, 依然可以由两个状态推出来
第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1][1]
第i天卖出股票,所得现金就是按照今天股票价格卖出后所得现金即:prices[i] + dp[i - 1][0]
注意这里和121. 买卖股票的最佳时机就是一样的逻辑,卖出股票收获利润(可能是负值)天经地义!
代码如下:(注意代码中的注释,标记了和121.买卖股票的最佳时机唯一不同的地方)
代码实现
class Solution {
public:int maxProfit(vector<int>& prices) {vector<vector<int>> dp(prices.size(),vector<int> (2));dp[0][0]=-prices[0];for (int i = 1; i < prices.size(); i++) {dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]); // 注意这里是和121. 买卖股票的最佳时机唯一不同的地方。dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);}return dp[prices.size()-1][1];}
};
思考总结
买入股票的时候,可能会有之前买卖的利润即:dp[i - 1][1],所以dp[i - 1][1] - prices[i]。
相关文章:

算法训练营day49|动态规划 part10:(LeetCode 121. 买卖股票的最佳时机、122.买卖股票的最佳时机II)
121. 买卖股票的最佳时机 题目链接🔥 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大…...
Swagger 使用教程
Swagger 官网: API Documentation & Design Tools for Teams | Swagger 整合swagger 依赖: springfox-swagger2 springfox-swagger-ui <dependency> <groupId>io.springfox</groupId> <artifactId>springfox-swagger2</a…...

单例模式-饿汉模式、懒汉模式
单例模式,是设计模式的一种。 在计算机这个圈子中,大佬们针对一些典型的场景,给出了一些典型的解决方案。 目录 单例模式 饿汉模式 懒汉模式 线程安全 单例模式 单例模式又可以理解为是单个实例(对象) 在有些场…...
UG\NX二次开发 复制3元素的double数组到另一个数组 UF_VEC3_copy
文章作者:里海 来源网站:王牌飞行员_里海_里海NX二次开发3000例,里海BlockUI专栏,C\C++-CSDN博客 简介: UG\NX二次开发 复制3元素的double数组到另一个数组 UF_VEC3_copy。仔细看第二段代码 。 效果: 代码: #include "me.hpp"void ufusr(char* param, …...

骨传导耳机对人体有危险吗?会损害听力吗?
如果在使用骨传导耳机的时候控制好时间和音量,是不会对人体带来危险和造成伤害的。 下面跟大家解释一下为什么骨传导耳机对人体没有危害,最大的原因就是骨传导耳机不需要空气传导,而是通过颅骨传到听觉中枢,传输过程中几乎没有噪…...
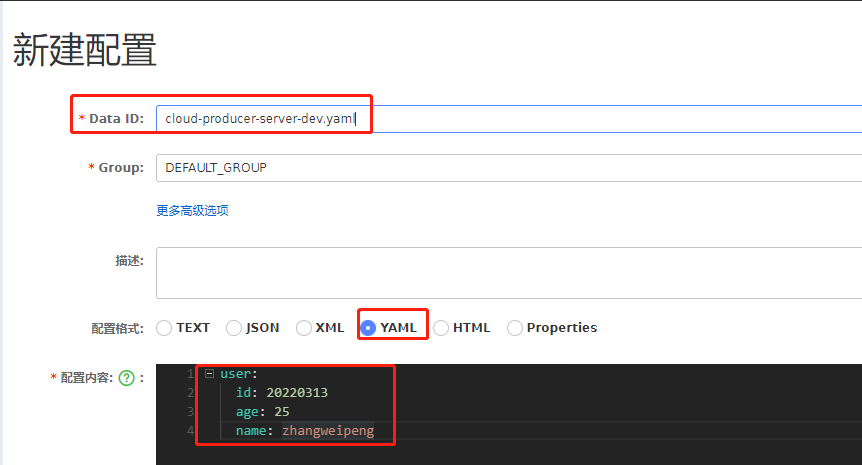
Spring Boot @Value读不到Nacos配置中心的值。(properties配置文件)
读不到配置中心的值, 配置中心的配置文件名字(Data ID的值)要以.properties结尾。 如果是yaml,就以yaml命名。...

Rocky Linux怎么安装mysql
Rocky Linux怎么安装mysql 在Rocky Linux上安装MySQL可以通过以下步骤实现: 更新软件包列表 ⭐️⭐️⭐️必要的,必须更新,更新会顺利很多!!!⭐️⭐️⭐️ 在安装MySQL之前,建议先更新软件包…...

轻量级软件FastGithub实现稳定访问github
当我们想访问全球最大的“同性交友网站”https://github.com/ 时,总会出现无法访问的界面,令人非常苦恼:幸运的是,有一种轻量级的软件可以帮助我们稳定地访问GitHub,那就是FastGithub。 什么是FastGithub?…...
芯科蓝牙BG27开发笔记6-精简第一个程序
1. 这些IO的控制代码在哪里? 还是蓝牙点灯程序: 首先需要对pinout做一些精简: 为了简化工程,去掉了不必要的IO。 至于PTI接口是什么,怎么用,不知道,现在不考虑: 但是提出以下问题…...

Android8.1 hal 加载wifi ko模块流程
Android如果发现wifi没有正常启动,从下面两个方面 1.是否正常编译出wifi ko文件,如果没有,说明编译的有问题,ko文件的地址vendor/lib/module/devices/wifi 2.如果有编译出ko文件,但还提示Wifi HAL start failed之类的…...
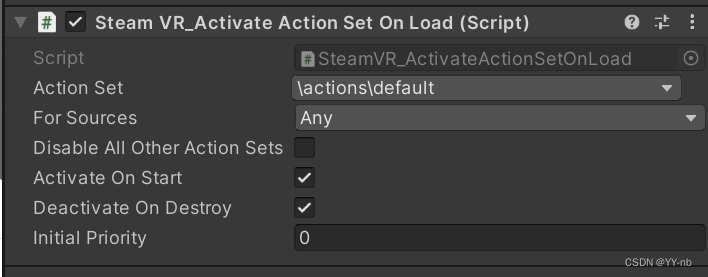
Unity SteamVR 开发教程:SteamVR Input 输入系统(2.x 以上版本)
文章目录 📕前言📕教程说明📕导入 SteamVR 插件📕SteamVR Input 窗口⭐action.json 文件⭐窗口面板⭐SteamVR_Input 目录 📕SteamVR 动作的类型⭐Boolean⭐Single⭐Vector2⭐Vector3⭐Pose⭐Skeleton⭐Vibration &…...

PyTorch中,卷积层、池化层、转置卷积层输出特征图形状计算公式总结
在PyTorch中,卷积层(Convolutional Layer)、池化层(Pooling Layer,例如最大池化层)、以及转置卷积层(Transpose Convolutional Layer,也称为反卷积层或上采样层)的输出特…...

Git Cherry Pick命令
1. 简介 Git是一款分布式版本控制系统,它提供了许多强大的功能来管理代码的版本和变更。其中之一就是cherry-pick命令,它允许我们选择某个分支上的一个或多个提交,并将它们应用到当前分支上。这个功能非常有用,可以帮助我们在不合…...

算法:经典贪心算法--跳一跳[2]
1、题目: 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处: 返回到达 nums[n - 1] 的最小跳跃次数。生…...

Vue 和 React 前端框架的比较
一、什么是Vue? Vue[1] 是一个用于构建用户界面的渐进式、可逐步采用的 JavaScript 框架。它由 Evan You[2] 于 2014 年创建,并由一个活跃的开发者社区负责维护。 Vue 设计得非常轻量级、灵活和强大。它建立在一个基于组件的架构上,以组件为…...
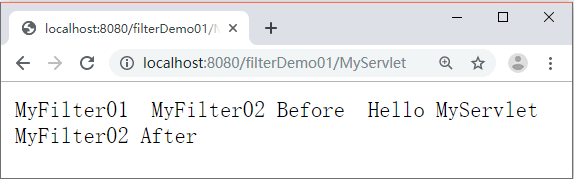
【Java】什么是过滤器链(FilterChain )?哪些场景可以使用过滤器链?
文章目录 前言1、创建过滤器2、修改 web.xml3、运行项目并查看结果 前言 在一个 Web 应用程序中可以注册多个 Filter 程序,每个 Filter 程序都可以针对某一个 URL 进行拦截。如果多个 Filter 程序都对同一个 URL 进行拦截,那么这些 Filter 就会组成一个…...
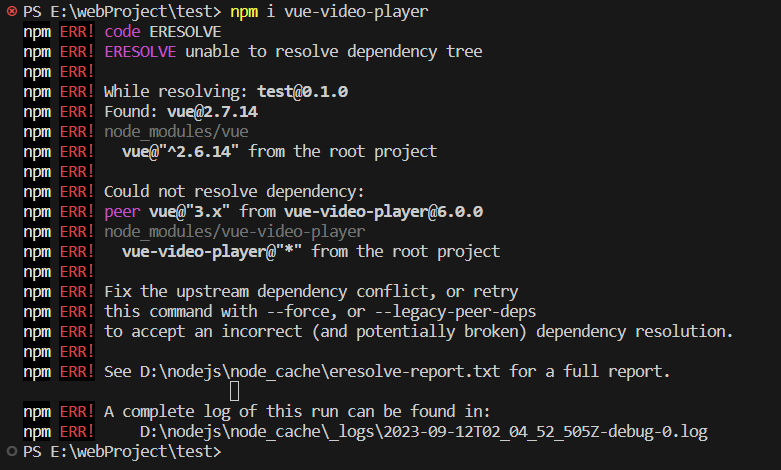
Vue-video-player下载失败(npm i 报错)
Vue-video-player下载失败 最近在做项目时涉及到视频的播放组件,看了一下选择了Vue-video-player这个工具,实际在操作中是遇到许多问题的。 Q1:不支持谷歌 对于 “vue-video-player” 使用时出现 Adobe Flash 不再支持的提示,这是因为 Ado…...

数据在内存中的存储(1)
目录 1、整数在内存中的存储 原码、反码、补码: 2、大小端: 前提须知: 大小端存储方式: 字节的顺序: 概念: 判断机器是大端还是小端: 代码展示: 代码优化1.0: …...

LINUX常用命令练习
显示LINUX系统当前的日期和时间。 date以 yyyy/mm/dd的格式显示系统当前的日期 date %Y/%m/%d以 yyyy-mm-dd的格式显示系统当前的日期 date %Y-%m-%d查看在线用户信息 who显示当前月份的日历 cal显示2023年整年的日历 cal 2023显示2023年9月的日历 cal 9 2023查看LINUX系统的Sh…...

2022年全国研究生数学建模竞赛华为杯C题汽车制造涂装-总装缓存调序区调度优化问题求解全过程文档及程序
2022年全国研究生数学建模竞赛华为杯 C题 汽车制造涂装-总装缓存调序区调度优化问题 原题再现: 背景介绍 汽车制造厂主要由焊装车间、涂装车间、总装车间构成,每个车间有不同的生产偏好,如:焊装车间由于车身夹具的限制偏向最…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

Yii2项目自动向GitLab上报Bug
Yii2 项目自动上报Bug 原理 yii2在程序报错时, 会执行指定action, 通过重写ErrorAction, 实现Bug自动提交至GitLab的issue 步骤 配置SiteController中的actions方法 public function actions(){return [error > [class > app\helpers\web\ErrorAction,],];}重写Error…...
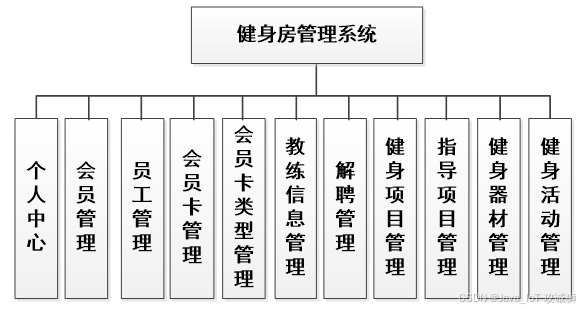
基于django+vue的健身房管理系统-vue
开发语言:Python框架:djangoPython版本:python3.8数据库:mysql 5.7数据库工具:Navicat12开发软件:PyCharm 系统展示 会员信息管理 员工信息管理 会员卡类型管理 健身项目管理 会员卡管理 摘要 健身房管理…...
