蓝桥杯官网填空题(星期几)
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
1949 年的国庆节( 10 月 1 日)是星期六。
今年(2012)的国庆节是星期一。
那么,从建国到现在,有几次国庆节正好是星期日呢?
不要求写出具体是哪些年,只要一个数目!
运行限制
- 最大运行时间:1s
- 最大运行内存: 128M
import java.util.Scanner;public class Main {public static void main(String[] args) {int ans=0;int week=6;for(int i=1950;i<=2011;i++){//根据题目已知1949年和2012年国庆节不是星期日if(i%400==0||(i%4==0&&i%100!=0)){week=week+366%7;//每年年份取模7,看余数为星期几,再加上6}else{week=week+365%7;}if(week%7==0){//若为7的倍数,则说明这天为星期日ans++;}}System.out.println(ans);}
}相关文章:
)
蓝桥杯官网填空题(星期几)
题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 1949 年的国庆节( 10 月 1 日)是星期六。 今年(2012)的国庆节是星期一。 那么,从建国到现在࿰…...
《向量数据库指南》——向量数据库会是 AI 的“iPhone 时刻”吗?
最近一年,以 ChatGPT、LLaMA 为代表的大语言模型的兴起,将向量数据库的发展推向了新的高度。 向量数据库是一种在机器学习和人工智能领域日益流行的新型数据库,它能够帮助支持基于神经网络而不是关键字的新型搜索引擎。向量数据库不同于传统的关系型数据库,例如 PostgreSQ…...
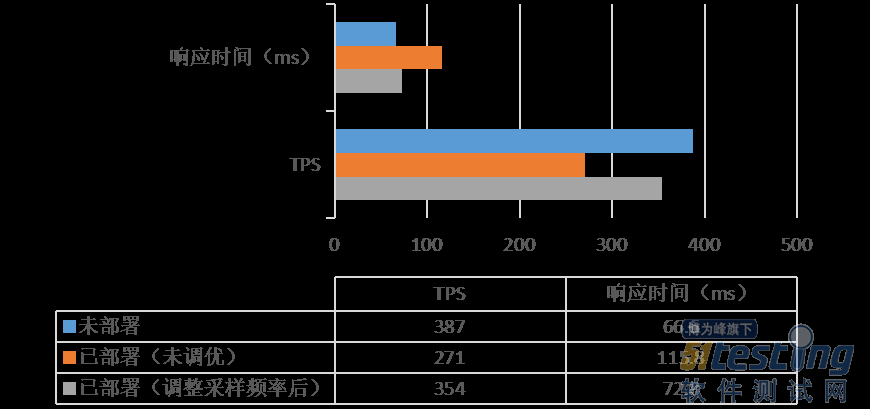
案例实践丨基于SkyWalking全链路监控的微服务系统性能调优实践篇
1背景 随着开源社区和云计算的快速推进,云原生微服务作为新型应用系统的核心架构,得到了越来越广泛的应用。根据Gartner对微服务的定义:“微服务是范围狭窄、封装紧密、松散耦合、可独立部署且可独立伸缩的应用程序组件。” 微服务之父&…...
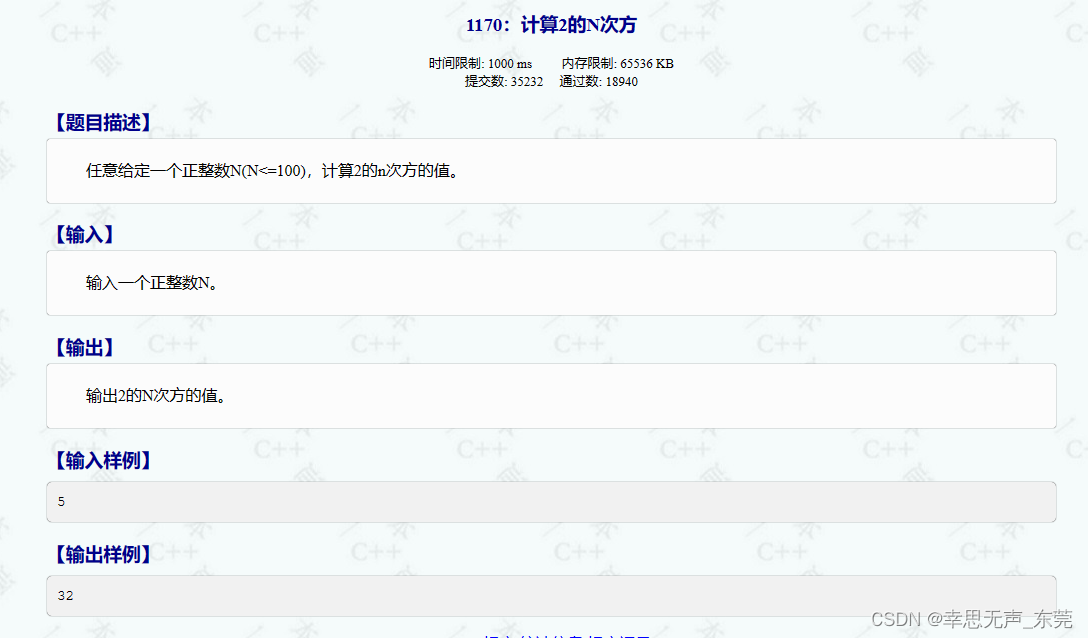
C++信息学奥赛1170:计算2的N次方
#include <iostream> #include <string> #include <cstring>using namespace std;int main() {int n;cin >> n; // 输入一个整数nint arr[100];memset(arr, -1, sizeof(arr)); // 将数组arr的元素初始化为-1,sizeof(arr)表示arr数组的字节…...

windos本地文件上传到ubuntu
如何把本地文件放到服务器上 scp /path/to/local/file usernameserver:/path/to/remote/directoryusernameserver 是服务器名和IP...

做软件测试,掌握哪些技术才能算作“测试大佬”?
一、过硬的基础能力 其实所有的测试大佬都是从底层基础开始的,随着时间,经验的积累慢慢变成大佬。要想稳扎稳打在测试行业深耕,成为测试大牛,首当其冲的肯定就是拥有过硬的基础,所有的基础都是根基,后期所有…...

【算法与数据结构】530、LeetCode二叉搜索树的最小绝对差
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:二叉搜索树的性质是左子树的所有节点键值小于中间节点键值,右子树的所有节点键值大于中间节…...

input输入事件
我要实现input输入框一边输入,一边在控制台输出结果 现有如下代码 <body><input type"text" onchange"myFunction()" /><script>function myFunction(){console.log(999)}</script> </body> 当敲下回车键后才会…...
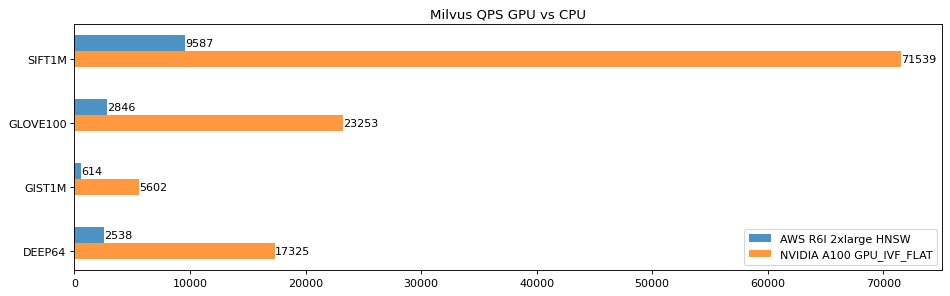
接入 NVIDIA A100、吞吐量提高 10 倍!Milvus GPU 版本使用指南
Milvus 2.3 正式支持 NVIDIA A100! 作为为数不多的支持 GPU 的向量数据库产品,Milvus 2.3 在吞吐量和低延迟方面都带来了显著的变化,尤其是与此前的 CPU 版本相比,不仅吞吐量提高了 10 倍,还能将延迟控制在极低的水准。…...
php://filter协议在任意文件读取漏洞(附例题)
php://filter php://fiter 中文叫 元器封装,咱也不知道为什么这么翻译,目前我的理解是可以通过这个玩意对上面提到的php IO流进行处理,及现在可以对php的 IO流进行一定操作。 过滤器:及通过php://filter 对php 的IO流进行的具体…...
【Redis】1、NoSQL之Redis的配置及优化
关系数据库与非关系数据库 关系型数据库 关系型数据库是一个结构化的数据库,创建在关系模型(二维表格模型)基础上,一般面向于记录。 SQL 语句(标准数据查询语言)就是一种基于关系型数据库的语言&a…...

9.5QTday6作业
面试题1:c语言中的static和c中的static的用法 在c语言中: 1.static修饰的全局变量作用域限制在当前文件,无法被外部文件所引用。2.static修饰的局部变量延长生命周期,但不改变作用域,同样无法被外部文件所引用。3.st…...
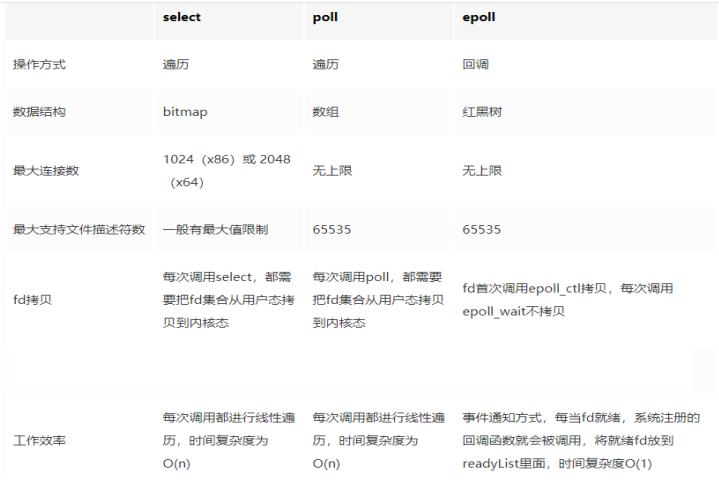
Redis I/O多路复用机制
一、基础回顾 1.1 多路复用要解决什么问题 并发多客户端连接场景,在多路复用之前最简单和典型的方案就是同步阻塞网络IO模型。 这种模式的特点就是用一个进程来处理一个网络连接(一个用户请求),比如一段典型的示例代码如下。 直接调用 recv 函数从一个 socket 上…...

Matlab 2016安装MinGW-w64-4.9.2
Matlab 2016安装MinGW-w64-4.9.2 项目需求:需要将matlab中的.m文件编译为cpp文件 .dll .h .lib。 我相信大家在对matlab2016安装MinGW-w64出现了各种各样的问题。如:4.9.2安装失败;安装了其他版本但是matlab检测不到,或者其他各种…...
Tomcat配置ssl、jar包
Tomcat配置ssl 部署tomcat服务,项目做到用https访问,使用nginx去做,访问任意一个子网站,都是https 或者 医美项目需要 上传jdk 456 tomcat war包 [nginx-stable] namenginx stable repo baseurlhttp://nginx.org/packages/…...

Unity中Shader实现UI去色功能的实现思路
文章目录 前言一、在开发过程中,在UI中会涉及一些需要置灰UI的需求,有很多实现的方法1、做两套纹理,通过程序控制切换2、使用shader实现对纹理去色 二、这里主要记录用shader实现的思路1、基础纹理的采样2、支持组件中的调色3、遮罩功能4、去…...

Python垃圾回收机制详解:引用计数与循环垃圾收集器
文章目录 Python垃圾回收机制引用计数机制循环垃圾收集器小结详细讲解及实操1. 程序中的垃圾问题2. 垃圾的定义3. 自动垃圾回收机制4. 示例:使用del方法删除垃圾对象5. 手动处理垃圾回收6. 结束程序7. 垃圾回收的自动处理8. 结束程序 python精品专栏推荐python基础知…...
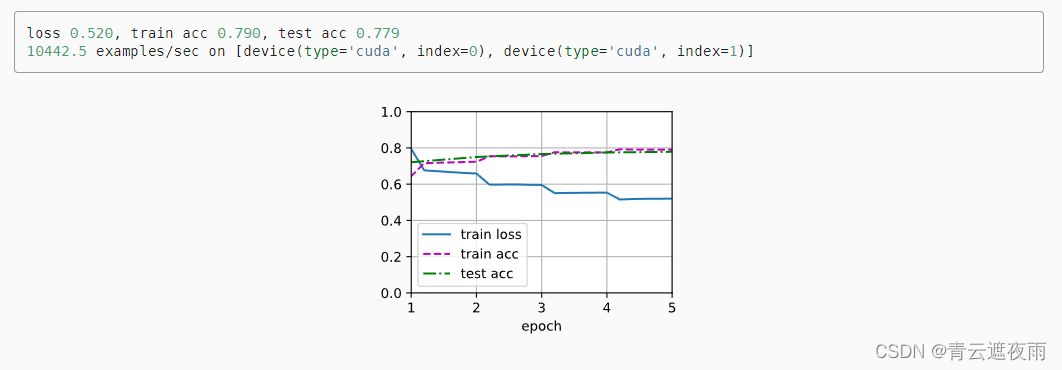
自然语言处理应用(三):微调BERT
微调BERT 微调(Fine-tuning)BERT是指在预训练的BERT模型基础上,使用特定领域或任务相关的数据对其进行进一步训练以适应具体任务的需求。BERT(Bidirectional Encoder Representations from Transformers)是一种基于Tr…...

MySQL基础【学习至基本语句】
一、安装与配置 1、安装 yum install -y mysql-server.x86_642、MySQL安装完成后,启动报错,查看MySQL的状态,发现是3306端口被占用 [rootiZ56kkvaq4nlfhZ etc]# systemctl status mysqld.service ● mysqld.service - MySQL 8.0 database …...
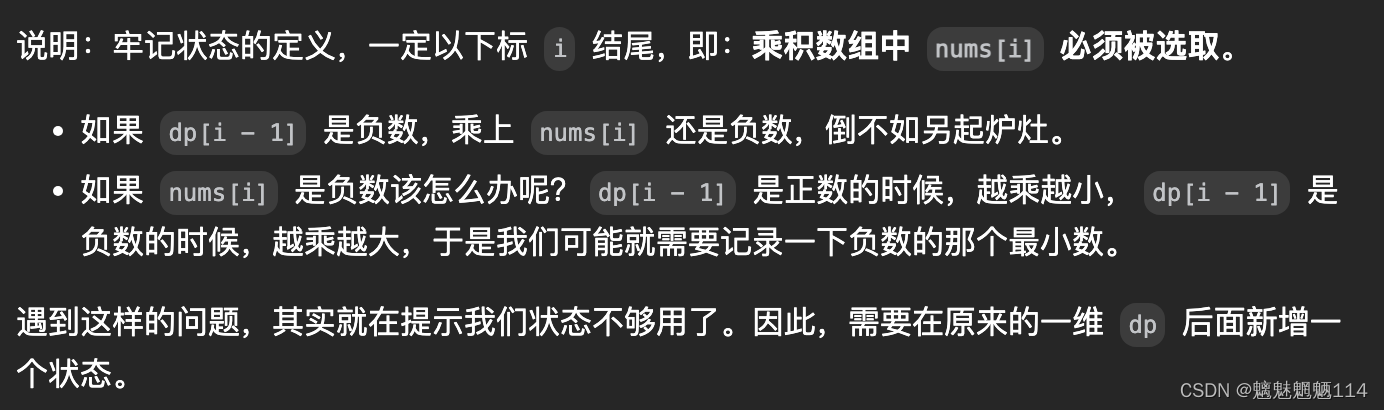
Leetcode152. 连续子数组的最大乘积
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。 测试用例的答案是一个 32…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...
