线性代数的本质(九)——二次型与合同
文章目录
- 二次型与合同
- 二次型与标准型
- 二次型的分类
- 度量矩阵与合同
二次型与合同
二次型与标准型
Grant:二次型研究的是二次曲面在不同基下的坐标变换
由解析几何的知识,我们了解到二次函数的一次项和常数项只是对函数图像进行平移,并不会改变图形的形状和大小。以一元二次函数为例

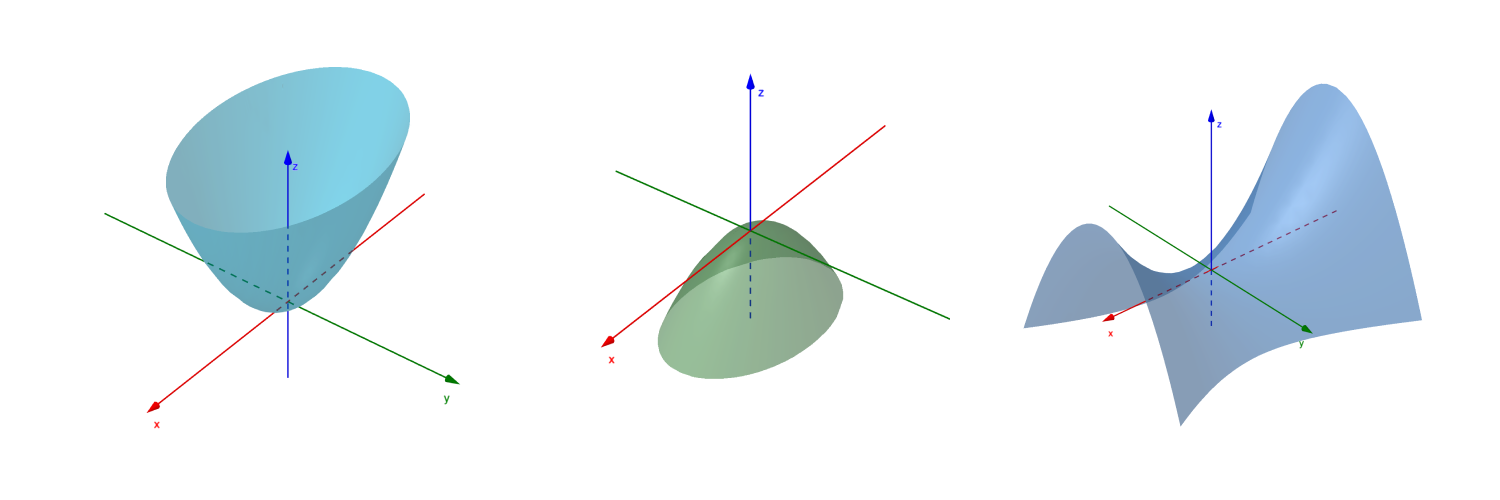
而二次函数的二次项控制函数图像的大小和形状。以二元二次函数为例,观察 f ( x , y ) = 1 f(x,y)=1 f(x,y)=1 的截面图形

线性代数主要研究这些图形的二次项,通过线性变换使二次曲面变得规范简洁。
定义: n n n 元二次齐次多项式
f ( x 1 , ⋯ , x n ) = a 11 x 1 2 + 2 a 12 x 1 x 2 + ⋯ + 2 a 1 n x 1 x n + a 22 x 2 2 + 2 a 23 x 2 x 3 + ⋯ + 2 a 2 n x 2 x n + a n n x n 2 \begin{aligned} f(x_1,\cdots,x_n)=&a_{11}x_1^2+2a_{12}x_1x_2+\cdots+2a_{1n}x_1x_n \\ &+a_{22}x_2^2+2a_{23}x_2x_3+\cdots+2a_{2n}x_2x_n \\ &+a_{nn}x_n^2 \end{aligned} f(x1,⋯,xn)=a11x12+2a12x1x2+⋯+2a1nx1xn+a22x22+2a23x2x3+⋯+2a2nx2xn+annxn2
称为二次型(quadratic form),这其实是二次曲面在一组坐标基下的解析表达式。
利用矩阵乘法,二次型可简记为
f = [ x 1 x 2 ⋯ x n ] [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] [ x 1 x 2 ⋮ x n ] = x T A x f=\begin{bmatrix}x_1&x_2&\cdots&x_n\end{bmatrix} \begin{bmatrix} a_{11}&a_{12}&\cdots&a_{1n} \\ a_{21}&a_{22}&\cdots&a_{2n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{m1}&a_{m2}&\cdots&a_{mn} \\ \end{bmatrix} \begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix} =\mathbf x^TA\mathbf x f=[x1x2⋯xn] a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn x1x2⋮xn =xTAx
其中 A A A 是对称阵,其主对角线元素是平方项的系数,其余元素 a i j = a j i a_{ij}=a_{ji} aij=aji 是二次项 x i x j x_ix_j xixj 系数 2 a i j 2a_{ij} 2aij 的一半。显然,对称矩阵 A A A 与二次型 f f f 是相互唯一确定的。矩阵 A A A 及其秩分别称为二次型的矩阵和秩。
在某些情况下,没有交叉乘积项的二次型会更容易使用,即通过线性变换 x = C y \mathbf x=C\mathbf y x=Cy 来消除交叉乘积项
f = x T A x = x = C y y T ( C T A C ) y = y T Λ y f=\mathbf x^TA\mathbf x\xlongequal{\mathbf x=C\mathbf y}\mathbf y^T(C^TAC)\mathbf y=\mathbf y^T\Lambda\mathbf y f=xTAxx=CyyT(CTAC)y=yTΛy
由于矩阵 A A A 是对称阵,由上节对称矩阵的对角化知道,总有正交矩阵 C C C,使
C − 1 A C = C T A C = Λ C^{-1}AC=C^TAC=\Lambda C−1AC=CTAC=Λ
而 Λ \Lambda Λ 的对角线元素是 A A A 的特征值,于是二次型可简化为
f = λ 1 y 1 2 + λ 2 y 2 2 + ⋯ + λ n y n 2 f=\lambda_1y_1^2+\lambda_2y_2^2+\cdots+\lambda_ny_n^2 f=λ1y12+λ2y22+⋯+λnyn2
这种只含平方项的二次型称为标准型(standard form)。显然,标准形的矩阵是对角阵。任何二次型都可通过正交变换化为标准型。系数全为 +1,-1或 0 的标准型叫做规范型(gauge form)。
定义:设 A A A和 B B B是 n n n阶矩阵,若有 n n n阶可逆矩阵 C C C,使
B = C T A C B=C^TAC B=CTAC
则称矩阵 A A A和 B B B合同,记为 A ≃ B A\simeq B A≃B 。显然,合同矩阵即为二次型在不同基下的矩阵。
性质:设矩阵 A ≃ B A\simeq B A≃B
- 若 A A A 为对称阵,则 B B B 也为对称阵;
- 合同矩阵的秩相等 rank ( A ) = rank ( B ) \text{rank}(A)=\text{rank}(B) rank(A)=rank(B);
化二次型为标准型的三种方法:
- 求矩阵 A A A 的特征值和特征向量化为标准型;
- 使用多项式配方法化为标准型;
- 使用初等变换法将上方的矩阵 A A A 的位置变为对角阵(左乘为行变换,不影响下方单位阵变换)
[ A I ] → [ C T A C C ] \begin{bmatrix}A\\I\end{bmatrix}\xrightarrow{}\begin{bmatrix}C^TAC\\C\end{bmatrix} [AI][CTACC]
例:将椭圆方程 5 x 1 2 − 4 x 1 x 2 + 5 x 2 2 = 48 5x_1^2-4x_1x_2+5x_2^2=48 5x12−4x1x2+5x22=48 标准化
解:二次型的矩阵 A = [ 5 − 2 − 2 5 ] A=\begin{bmatrix}5&-2\\-2&5\end{bmatrix} A=[5−2−25] ,特征值分别为 3和 7,对应的单位特征向量为
u 1 = [ 1 / 2 1 / 2 ] , u 2 = [ − 1 / 2 1 / 2 ] \mathbf u_1=\begin{bmatrix}1/\sqrt{2}\\1/\sqrt{2}\end{bmatrix}, \mathbf u_2=\begin{bmatrix}-1/\sqrt{2}\\1/\sqrt{2}\end{bmatrix} u1=[1/21/2],u2=[−1/21/2]
可使用特征向量 u 1 , u 2 \mathbf u_1,\mathbf u_2 u1,u2 作为二次型的标准正交基。正交变换矩阵和标准型矩阵分别为
C = ( u 1 , u 2 ) = [ 1 / 2 − 1 / 2 1 / 2 1 / 2 ] , Λ = [ 3 0 0 7 ] C=(\mathbf u_1,\mathbf u_2)=\begin{bmatrix}1/\sqrt{2}&-1/\sqrt{2}\\1/\sqrt{2}&1/\sqrt{2}\end{bmatrix},\quad \Lambda=\begin{bmatrix}3&0\\0&7\end{bmatrix} C=(u1,u2)=[1/21/2−1/21/2],Λ=[3007]
C C C 可将 A A A 正交对角化, Λ = C T A C \Lambda=C^TAC Λ=CTAC 。所以正交变换 x = P y \mathbf x=P\mathbf y x=Py 得到的标准型为
y T C y = 3 y 1 2 + 7 y 2 2 \mathbf y^TC\mathbf y=3y_1^2+7y_2^2 yTCy=3y12+7y22
新的坐标轴如图

二次型的分类
定义:设二次型 f = x T A x f=\mathbf x^TA\mathbf x f=xTAx ,如果对于任何 x ≠ 0 \mathbf x\neq 0 x=0
- 都有 f ( x ) > 0 f(\mathbf x)>0 f(x)>0,则称 f f f 为正定二次型,称 A A A 为正定矩阵;
- 都有 f ( x ) < 0 f(\mathbf x)<0 f(x)<0,则称 f f f 为负定二次型,称 A A A 为负定矩阵;
- 如果 f ( x ) f(\mathbf x) f(x) 既有正值又有负值,则称为不定二次型;
从上节可以看出二次型的标准型是不唯一的,但二次型的秩是唯一的,在化成标准型的过程中是不变的,即标准型中含有的非零平方项的个数是不变的。
惯性定理:二次型和标准型中系数为正的平方项的个数相同,称为正惯性指数;系数为负的平方项的个数也相同,称为负惯性指数;正负惯性指数之差称为符号差。
定理:
- n n n元二次型为正定的充要条件是它的正惯性指数为 n n n;
- 对称阵 A A A正定 ⟺ \iff ⟺ 特征值全为正 ⟺ \iff ⟺ 与单位阵合同 A ≃ I A\simeq I A≃I ;
- 对称阵 A A A 正定 ⟹ \implies ⟹ A − 1 A^{-1} A−1 正定;
度量矩阵与合同
Grant:合同矩阵为不同坐标系下的度量矩阵。
以二维空间为例,Grant 选用标准坐标系下的基向量 i , j \mathbf i,\mathbf j i,j,度量矩阵
A = [ ⟨ i , i ⟩ ⟨ i , j ⟩ ⟨ j , i ⟩ ⟨ j , j ⟩ ] A=\begin{bmatrix} \lang\mathbf i,\mathbf i\rang&\lang\mathbf i,\mathbf j\rang \\ \lang\mathbf j,\mathbf i\rang&\lang\mathbf j,\mathbf j\rang \end{bmatrix} A=[⟨i,i⟩⟨j,i⟩⟨i,j⟩⟨j,j⟩]
而 Jennifer 使用另外一组基向量 i ′ , j ′ \mathbf i',\mathbf j' i′,j′,过渡矩阵 P = [ a b c d ] P=\begin{bmatrix} a&b \\ c&d \end{bmatrix} P=[acbd]。即基向量 i ′ , j ′ \mathbf i',\mathbf j' i′,j′ 在 Grant 的坐标系下的坐标表示为
p 1 = [ a c ] , p 2 = [ b d ] \mathbf p_1=\begin{bmatrix} a \\ c \end{bmatrix},\quad \mathbf p_2=\begin{bmatrix} b \\ d \end{bmatrix} p1=[ac],p2=[bd]
因此, Jennifer 的基向量间的内积
⟨ i ′ , i ′ ⟩ = p 1 T A p 1 ⟨ i ′ , j ′ ⟩ = p 1 T A p 2 ⟨ j ′ , i ′ ⟩ = p 2 T A p 1 ⟨ j ′ , j ′ ⟩ = p 2 T A p 2 \lang\mathbf i',\mathbf i'\rang=\mathbf p_1^TA\mathbf p_1\\ \lang\mathbf i',\mathbf j'\rang=\mathbf p_1^TA\mathbf p_2 \\ \lang\mathbf j',\mathbf i'\rang=\mathbf p_2^TA\mathbf p_1 \\ \lang\mathbf j',\mathbf j'\rang=\mathbf p_2^TA\mathbf p_2 ⟨i′,i′⟩=p1TAp1⟨i′,j′⟩=p1TAp2⟨j′,i′⟩=p2TAp1⟨j′,j′⟩=p2TAp2
于是,Jennifer坐标系的度量矩阵
B = [ p 1 T A p 1 p 1 T A p 2 p 2 T A p 1 p 2 T A p 2 ] = [ p 1 T p 2 T ] A [ p 1 p 2 ] = P T A P B=\begin{bmatrix} \mathbf p_1^TA\mathbf p_1&\mathbf p_1^TA\mathbf p_2 \\ \mathbf p_2^TA\mathbf p_1&\mathbf p_2^TA\mathbf p_2 \end{bmatrix}= \begin{bmatrix} \mathbf p_1^T \\ \mathbf p_2^T \end{bmatrix}A\begin{bmatrix} \mathbf p_1 & \mathbf p_2 \end{bmatrix} =P^TAP B=[p1TAp1p2TAp1p1TAp2p2TAp2]=[p1Tp2T]A[p1p2]=PTAP
由此可知,合同矩阵刻画了两度量矩阵间的关系。
当然,也可通过两个向量的内积在不同的坐标系中的计算公式获得两个度量矩阵间的关系。由过渡矩阵知道,同一个向量从 Jennifer 的坐标到 Grant 的坐标变换公式为
y = P x \mathbf y=P\mathbf x y=Px
在 Jennifer 的坐标系中,两向量 u , v \mathbf u,\mathbf v u,v 的坐标为 x 1 , x 2 \mathbf x_1,\mathbf x_2 x1,x2 ,度量矩阵为 B B B 。内积计算公式
⟨ u , v ⟩ = x 1 T B x 2 \lang\mathbf u,\mathbf v\rang=\mathbf x_1^TB\mathbf x_2 ⟨u,v⟩=x1TBx2
在 Grant 的坐标系中,两向量 u , v \mathbf u,\mathbf v u,v 的的坐标为 y 1 , y 2 \mathbf y_1,\mathbf y_2 y1,y2,度量矩阵为 A A A 。内积计算公式
⟨ u , v ⟩ = y 1 T A y 2 = ( P x 1 ) T A ( P x 2 ) = x 1 T ( P T A P ) x 2 \lang\mathbf u,\mathbf v\rang=\mathbf y_1^TA\mathbf y_2 =(P\mathbf x_1)^TA(P\mathbf x_2)=\mathbf x_1^T(P^TAP)\mathbf x_2 ⟨u,v⟩=y1TAy2=(Px1)TA(Px2)=x1T(PTAP)x2
于是,我们得到了两坐标系中度量矩阵的关系
B = P T A P B=P^TAP B=PTAP
相关文章:

线性代数的本质(九)——二次型与合同
文章目录 二次型与合同二次型与标准型二次型的分类度量矩阵与合同 二次型与合同 二次型与标准型 Grant:二次型研究的是二次曲面在不同基下的坐标变换 由解析几何的知识,我们了解到二次函数的一次项和常数项只是对函数图像进行平移,并不会改变…...
STM32WB55开发(4)----配置串口打印Debug调试信息
STM32WB55开发----4.配置串口打印Debug调试信息 概述硬件准备视频教学样品申请选择芯片型号配置时钟源配置时钟树RTC时钟配置查看开启STM32_WPAN条件配置HSEM配置IPCC配置RTC启动RF开启蓝牙开启串口调试配置蓝牙参数设置工程信息工程文件设置Keil工程配置代码配置结果演示 概述…...

云原生服务无状态(Stateless)特性的实现
文章目录 为何要使用无状态服务?无状态服务的实现方法1. 会话状态外部化2. 负载均衡3. 自动伸缩4. 容器编排5. 数据存储6. 安全性 示例:使用Spring Boot实现无状态服务结论 🎉欢迎来到云计算技术应用专栏~云原生服务无状态(Statel…...
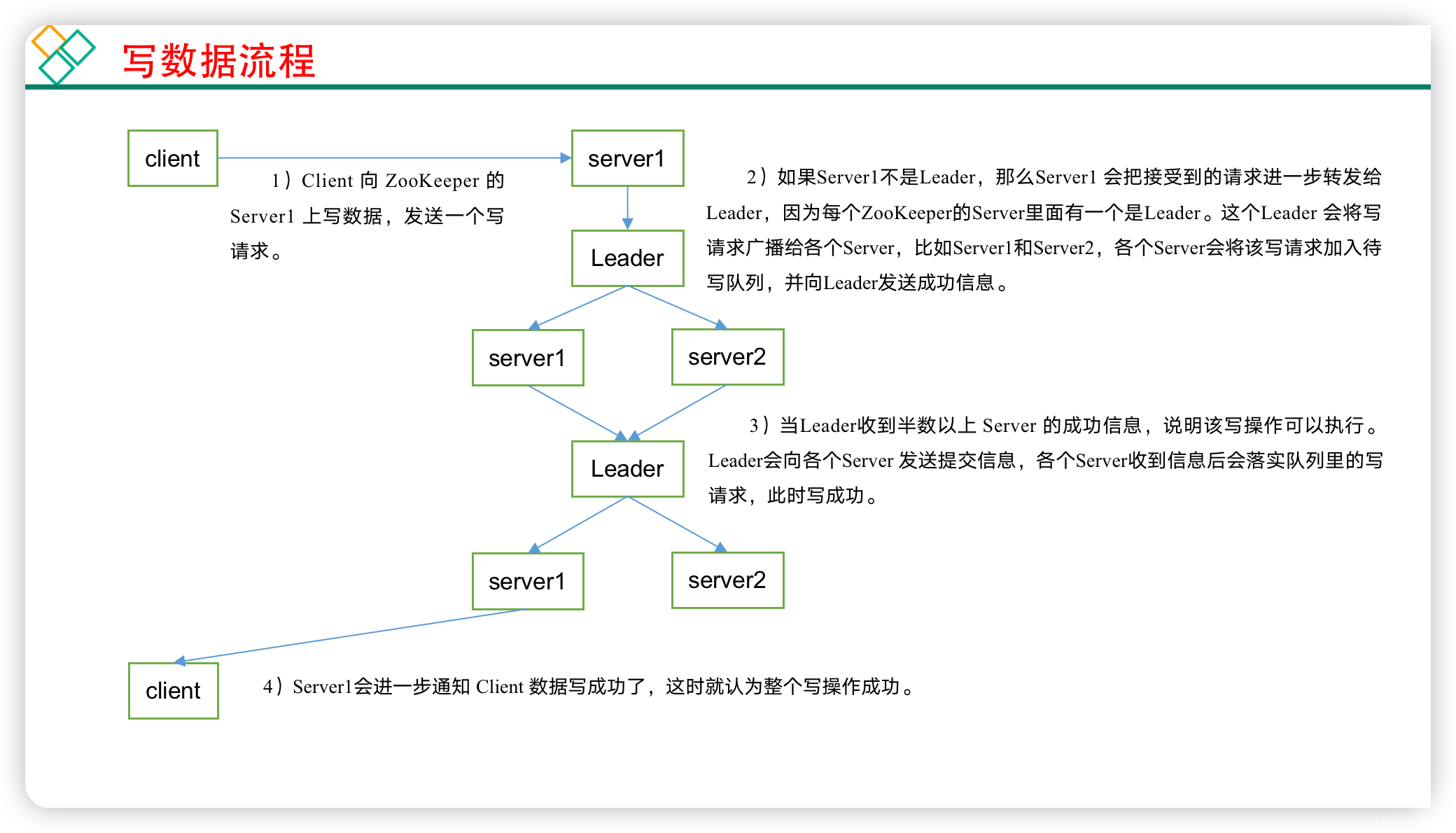
zookeeper最基础教程
文章目录 一、简介1、工作机制2、特点3、数据结构4、应用场景5、选举机制 二、软件安装1、单机版安装2、集群安装3、配置参数解读(zoo.cfg)4、ZK集群启动脚本 三、命令行操作1、语法2、使用3、节点相关4、监听器原理5、节点删除与查看 三、写数据流程 一、简介 1、工作机制 官…...

又一重磅利好来袭!Zebec Payroll 集成至 Nautilus Chain 主网
流支付协议 Zebec Protocol 正在积极的拓展自身生态,随着此前其全新路线图的发布,揭示了该生态从 Web3 世界向 Web2 世界跨越的决心。根据其最新路线图,Zebec Protocol 正在从最初构建在 Solana 上的流支付协议,拓展为囊括模块化公…...

NLP模型的tokenize方法中return_tensors参数
NLP模型的tokenize方法中return_tensors参数 在许多NLP模型的tokenize方法中,return_tensors参数可以指定tokenize之后返回的张量类型,常见的可选值包括: ‘tf’: 返回TensorFlow的张量对象Tensor。 ‘pt’: 返回PyTorch的张量对象torch.Tensor。 ‘np’: 返回NumPy的ndarray对…...
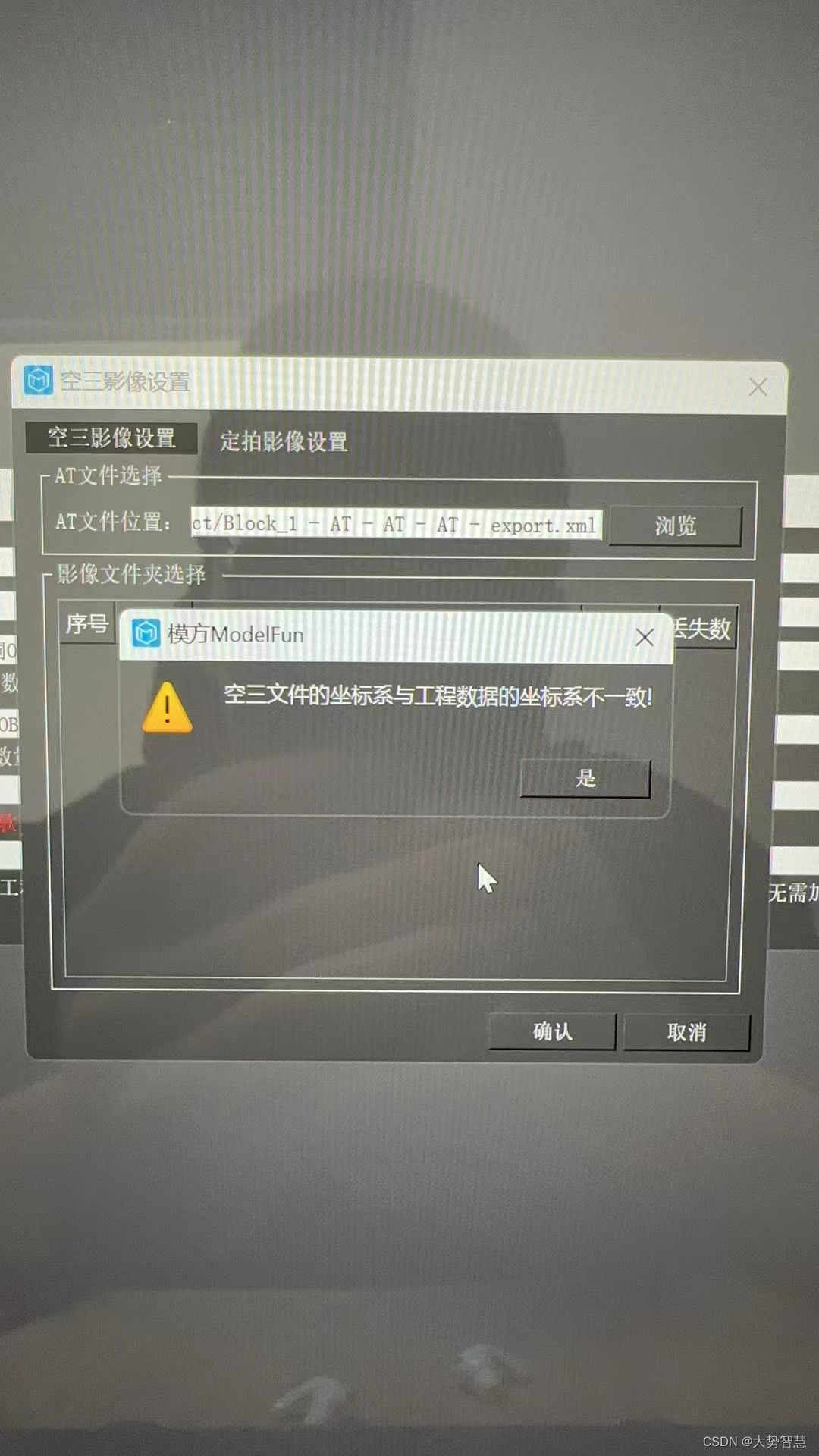
模方新建工程时,显示空三与模型坐标系不一致怎么解决
答:检查空三xml与模型的metadata.xml的坐标系是否一致,metadata文件是否有在data目录外面。 模方是一款针对实景三维模型的冗余碎片、水面残缺、道路不平、标牌破损、纹理拉伸模糊等共性问题研发的实景三维模型修复编辑软件。模方4.0新增单体化建模模块,…...

氧化锌避雷器绝缘电阻测试
氧化锌避雷器 绝缘电阻测试 试验目的 避雷器绝缘电阻包括本体绝缘电阻和底座绝缘电阻, 主要目的在于初步检查避雷 器内部是否受潮; 有并联电阻者可检查其通、 断、 接触和老化等情况。 试验设备 高压绝缘电阻测试仪 厂家: 湖北众拓高试 试验方法 本体绝缘电阻试验…...

链动2+1系统开发
什么是链动21模式? 链动21主要是一个集团队搭设、快速提升产品销量,与消费者做到合作共赢的一个商业模式,让用户在享受购物折扣的同时,也能获得相对收益,同时公司也能达到产品快速销售这样的一个目的,而链…...
AIGC(生成式AI)试用 4 -- 从模糊到精确
从模糊到精确,也许差异在于 更多的描述,更多的信息更具像的描述,更多的数据,更有效的信息主题明确和目标清晰层次感与条理性更简洁清晰的逻辑 “说清楚点,不太明白,提供更多的信息也许能知道要做什么。” …...

Linux中使用Docker安装ElasticSearch7.10.x集群
使用Docker安装ElasticSearch7.10.x单节点请访问这里 一、集群环境说明 服务器IP地址192.168.137.1,192.168.137.2,192.168.137.3 二、前期准备 1. 拉取镜像 docker pull elasticsearch:7.10.12. 首先需要创建一个用于生成秘钥的初始容器࿰…...
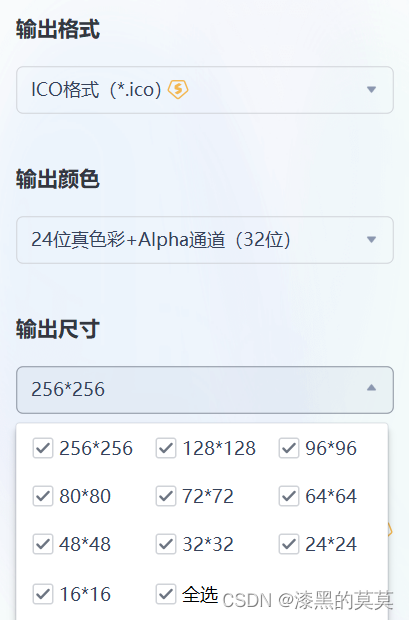
electron 左上角图标 dev(开发环境)可显示 build(打包)后无法显示
先说解决方法,用于作为图标的ico文件需要富集多种尺寸,必须包含256*256,且同时应当包含其他更小的尺寸。 例如: 接下来解释一下这么做的原因 ico是Iconfile的缩写,是Windows计算机中的一种图标文件格式,…...

全球与中国BGO晶体市场:增长趋势、竞争格局与前景展望
BGO晶体,全名为Bismuth Germanate Scintillation Crystal(铋锗酸盐闪烁晶体),是一种用于探测放射性粒子和射线的闪烁晶体材料。它的主要成分是铋氧化物(Bi4Ge3O12),其中铋和锗的特性使得这种晶体…...
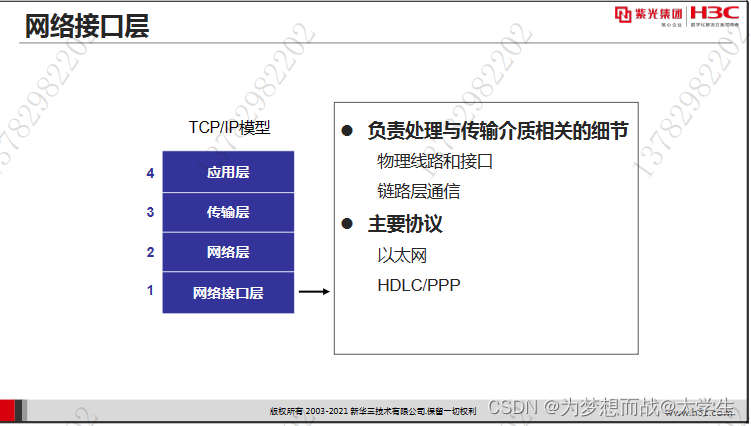
华三路由交换技术基础——计算机网络基础
计算机网络: 定义:一组具有自治权的计算机互联的集合 作用: 1.共享信息资源 2.分解式处理信息 4.负载均衡 5.综合信息服务 它是计算机技术与通信技术的两个领域的结合 一,计算机网络中的基本概念: 局域网ÿ…...

Docker搭建RK3568开发环境
推荐:Ubuntu 20.04 版本 Docker加速 # 编辑 Docker 配置文件 $ sudo vim /etc/docker/daemon.json# 加入以下配置项 {"registry-mirrors": ["https://dockerproxy.com","https://hub-mirror.c.163.com","https://mirror.baidu…...

【GAMES202】Real-Time Ray Tracing 1—实时光线追踪1
一、前言 这篇我们开始新的话题—Real-Time Ray Tracing简称RTRT,也就是实时光线追踪,关于光线追踪,我们已经不止一次提到过它的优点,无论是软阴影还是全局光照,光线追踪都很容易做,唯一的缺点就是速度太慢…...

Linux修复损坏的文件系统
如何判断文件系统是否损坏 当文件系统受损时,将会出现一些明显的迹象。例如,文件或文件夹无法访问、文件大小异常、系统启动慢或无法启动等。此外,系统也可能发出一些错误信息,如"Input/output error"、"Filesyst…...
三分钟学会一个新技能——使用Java操作Redis
目录 1、前置准备操作 1.1、为什么要进行前置准备操作 1.2、本地如何访问到云服务上Redis的6379端口号 1.3、配置步骤: 2、配置后本地主机如何操作 3、常用命令举例 3.1、通用命令举例 3.2、string相关命令举例 3.3、hash相关命令举例 3.4、list相关命令…...

Java学习笔记------内部类
内部类的定义: 在一个类的里面再定义一个类 内部类的使用场景: 内部类表示的事物是外部类的一部分(B类表示的事物是A类的一部分,且B单独存在没有意义)内部类单独出现没有任何意义 内部类的访问特点 内部类可以直接…...
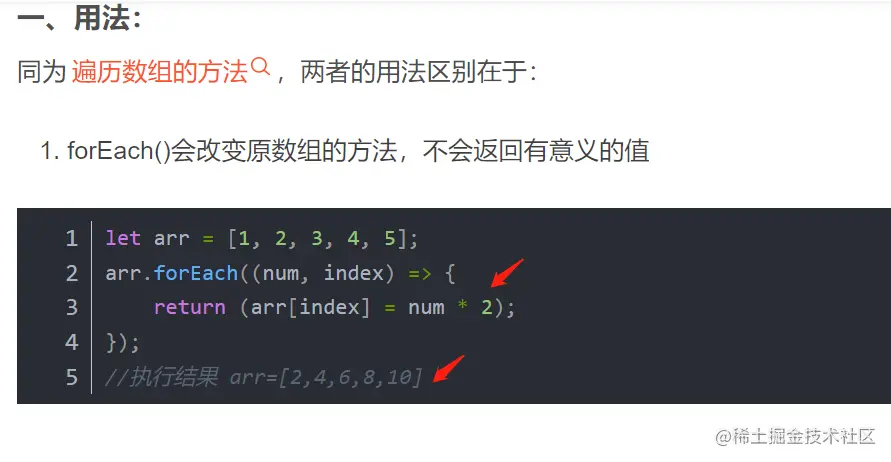
面试题:问js的forEach和map的区别
前端面试题库 (面试必备) 推荐:★★★★★ 地址:前端面试题库 【国庆头像】- 国庆爱国 程序员头像!总有一款适合你! 前言 为什么要写这么一篇文章,原因是今天下午水群的时候&…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...
