图神经网络系列之序章
文章目录
- 一、为什么需要图神经网络?
- 二、图的定义
- 1.图的定义和种类
- 2.一些关于图的重要概念
- 2.1 子图
- 2.2 连通图
- 2.3 顶点的度、入度和出度
- 2.4 边的权和网
- 2.5 稠密图、稀疏图
- 3.图的存储结构
- 3.1 邻接矩阵
- 3.2 邻接表
- 3.3 边集数组
- 3.4 邻接多重表
- 3.5 十字链表
- 3.6 链式前向星
- 三、图神经网络类别
一、为什么需要图神经网络?
随着机器学习、深度学习的发展,语音、图像、自然语言处理逐渐取得了很大的突破,然而语音、图像、文本都是很简单的序列或者网格数据,是很结构化的数据,深度学习很善于处理该种类型的数据(图1)。

然而现实世界中并不是所有的事物都可以表示成一个序列或者一个网格,例如社交网络、知识图谱、复杂的文件系统等(图2),也就是说很多事物都是非结构化的。
相比于简单的文本和图像,这种网络类型的非结构化的数据非常复杂,处理它的难点包括:
- 图的大小是任意的,图的拓扑结构复杂,没有像图像一样的空间局部性
- 图没有固定的节点顺序,或者说没有一个参考节点
- 图经常是动态图,而且包含多模态的特征
那么对于这类数据我们该如何建模呢?能否将深度学习进行扩展使得能够建模该类数据呢?这些问题促使了图神经网络的出现与发展。
二、图的定义
1.图的定义和种类
图可以用 G = ( V , E ) G=(V, E) G=(V,E)来表示,
其中
- V V V是顶点或节点的集合,
- E E E是边的集合,
- e i j = ( v i , v j ) ∈ E e_{ij}=(v_i, v_j)∈E eij=(vi,vj)∈E则表示从 v i v_i vi指向 v j v_j vj的边(有向图),或仅表示 v i v_i vi和 v j v_j vj之间的边(无向图)
- N ( v ) = { u ∈ V ∣ ( v , u ) ∈ E } N(v) = \left\{ u∈V|(v,u)∈E \right\} N(v)={u∈V∣(v,u)∈E}表示节点 v v v的邻域
图的种类主要包括有向图、无向图,再往下细分这两类又包括简单图、多重图、完全图
简单图:
①不存在重复边;②不存在顶点到自身的边
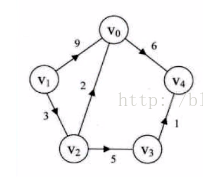
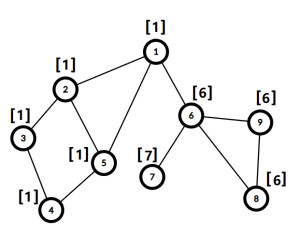
简单有向图(图左);简单无向图(图右)
多重图:
和简单图相对,图G中某两个结点之间的边数多于一条,又允许顶点通过同一条边和自己关联(即有自环)
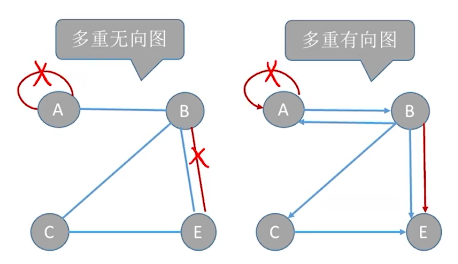
完全图:
任意两个顶点之间都存在边

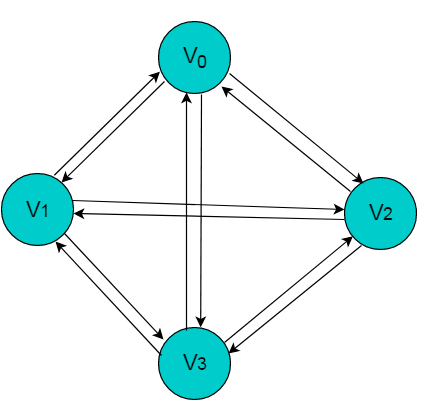
完全有向图(图左);完全无向图(图右)
2.一些关于图的重要概念
2.1 子图
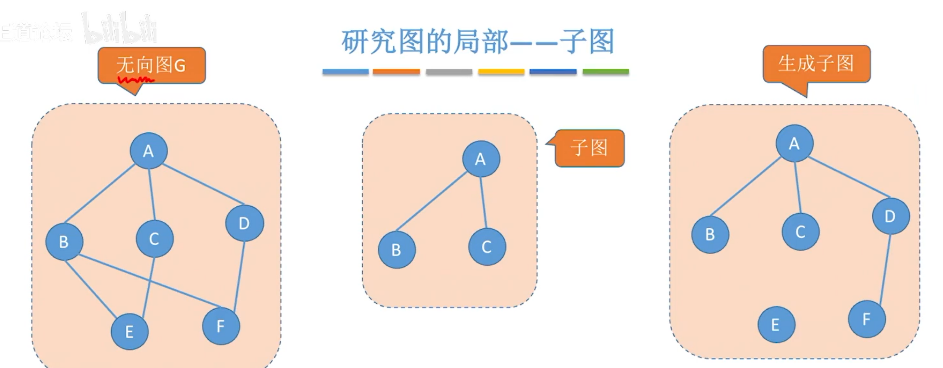
设有两个图G=(V, E)和G’=(V’, E’),若V’是V的子集, E’是E的子集,则称G’为G的子图,若满足V(G’)=V(G)的子图G’,则称其为G的生成子图。
2.2 连通图
指的是一个图中的每对顶点之间都存在至少一条路径,即从图中的任意一个顶点出发,都可以通过边的连通性到达图中的任何其他顶点。
连通图可以分为以下几种类型:
- 强连通图(Strongly Connected Graph):在一个有向图中,如果对于图中的任意两个顶点 u 和 v 都存在从 u 到 v 和从 v 到 u 的有向路径,那么该图是强连通图
- 无向连通图(Connected Graph):在一个无向图中,如果对于图中的任意两个顶点 u 和 v 都存在一条无向路径,那么该图是无向连通图
- 弱连通图(Weakly Connected Graph):在一个有向图中,如果将有向边的方向忽略,将其视为无向边后,得到的无向图是连通图,那么该图是弱连通图。
- 生成树(Tree):生成树是针对无向图的,它没有回路(环路)。连通图的生成树就是包含图中全部顶点的一个极小连通子图。
- 生成森林(Forest):生成森林是针对非连通图的,非连通图可分解为多个连通分量,而每个连通分量又各自对应多个生成树。
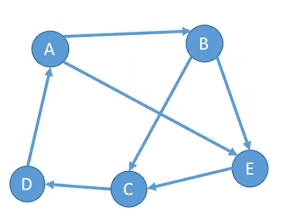
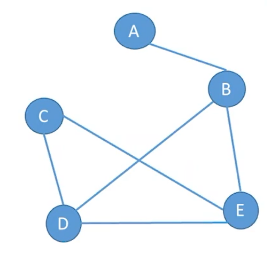
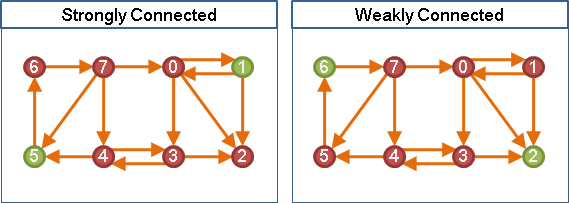
强连通图;无向连通图;强连通图;弱连通图
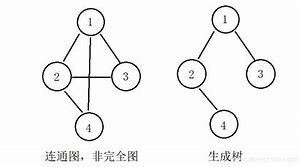
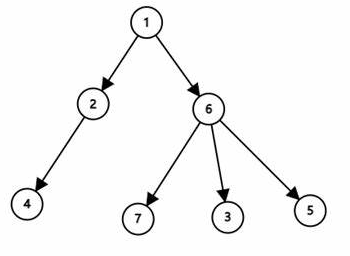
有向树:一个顶点的入度为0、其余顶点的入度均为1的有向图,称为有向树(右图)
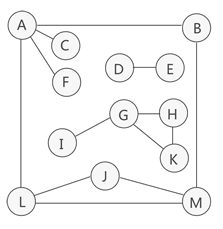

非连通图(左图);生成森林(右图)
2.3 顶点的度、入度和出度
图中每个顶点的度定义为以该项点为一个端点的边的数目。
- 对于无向图,顶点v的度是指依附于该顶点的边的条数,记为TD(v)
- 对于有向图,顶点v的度分为入度和出度,入度是以顶点v vv为终点的有向边的数目,记为ID(v); 而出度是以顶点v为起点的有向边的数目,记为OD(v)。顶点v的度等于其入度和出度之和
2.4 边的权和网
在一个图中,每条边都可以标上具有某种含义的数值,该数值称为该边的权值。这种边上带有权值的图称为带权图,也称网
2.5 稠密图、稀疏图
边数很少的图称为稀疏图,反之称为稠密图。稀疏和稠密本身是模糊的概念,稀疏图和稠密图常常是相对而言的。一般当图G满足 ∣ E ∣ < ∣ V ∣ l o g ∣ V ∣ |E| < |V|log|V| ∣E∣<∣V∣log∣V∣时,可以将G视为稀疏图;当图G满足 ∣ E ∣ |E| ∣E∣接近 ∣ V 2 ∣ |V^2| ∣V2∣时,可以将G视为稠密图
3.图的存储结构
图的表示包括邻接表、邻接矩阵、边集数组、邻接多重表、十字链表、链式前向星等,每种图的表示都有不同的用处,需要根据实际需求选择。
其中,比较标准和常规的表示方法有,邻接表、邻接矩阵和边集数组,这三种表示法都即可以表示无向图,也可以表示有向图。特殊一点的包括邻接多重表、十字链表和链式前向星。
- 邻接链表通常用来表示稀疏图,而邻接矩阵通常用来表示稠密图,另外,如果需要快速判断任意两个结点之间是否有边相连,可能也需要使用邻接矩阵表示法
- 邻接表
- 存各种图都很适合,除非有特殊需求(如需要快速查询一条边是否存在,且点数较少,可以使用邻接矩阵)。尤其适用于需要对一个点的所有出边进行排序的场合。
- 邻接表的一个潜在缺陷是无法快速判断一条边(u, v)是否是图中的一条边,唯一的办法是在邻接链表Adj[u]中搜索结点v。
- 邻接表还衍生出了一种逆邻接表,因为邻接表统计出度的效率较高,而入度需要遍历整个表才可以统计出来,而逆邻接表不需要遍历,直接就可以统计出每个结点的出度,这正好和邻接表相反。
- 邻接矩阵
- 邻接表的一个缺陷是无法快速判断一条边(u, v)是否是图中的一条边。而邻接矩阵克服了这个缺点,但付出的代价是更高的空间复杂度。
- 邻接矩阵只适用于没有重边(或重边可以忽略)的情况。其最显著的优点是可以 O ( 1 ) O(1) O(1)查询一条边是否存在。由于邻接矩阵在稀疏图上效率很低(尤其是在点数较多的图上,空间无法承受),所以一般只会在稠密图上使用邻接矩阵。
- 空间复杂度高
- 边集数组
- 由于直接存边的遍历效率低下,一般不用于遍历图。主要见到的就是在,最小生成树的 Kruskal 算法中,由于需要将边按边权排序,需要直接存边。在有时候,有可能需要多次建图(如建一遍原图,建一遍反图),此时既可以使用多个其它数据结构来同时存储多张图,也可以将边直接存下来,需要重新建图时利用直接存下的边来建图。
- 邻接多重表
- 邻接多重表用于表示无向图
- 邻接表虽然已经能够很好地表示无向图了,但是无向图访问或者删除一条边(Vi,Vj)时需要同时访问两个链表i和j并分别找到对应的边结点,这给针对图的边的操作(标记或删除)带来不便利。邻接多重表因此而演变过来的。当一个无向图需要频繁的修改时,邻接表表示法需要修改边两侧的结点对应的信息,而多重邻接表可以只修改一次,计算量节省了一半。
- 十字链表
- 十字链表用来表示有向图
- 十字链表是结合了邻接表和逆邻接表于一体的表示方法,用来表示有向图,综合了两种表示方法的优点,缺点是表示起来更加复杂。
- 链式前向星
- 链式前向星是一种静态链表存储,用边集数组和邻接表相结合,可以快速访问一个顶点的所有邻接点,在算法竞赛中广泛使用。
3.1 邻接矩阵
图的邻接矩阵(Adjacency Matrix) 存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息
下图是一个无向图和它的邻接矩阵
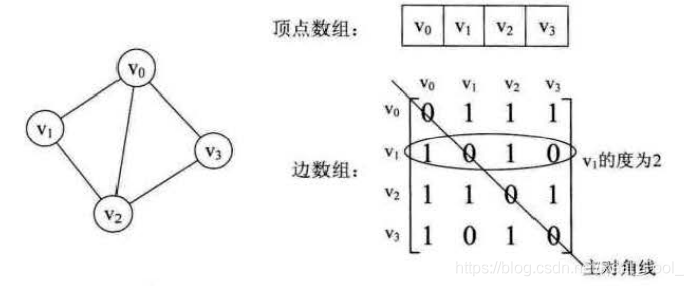
下图是一个有向图和它的邻接矩阵
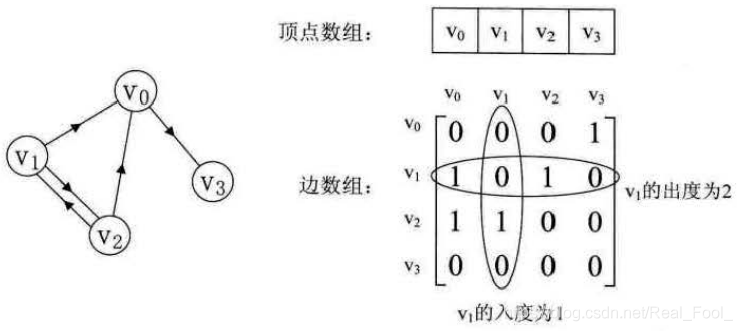
下图是一个有向带权图和它的邻接矩阵
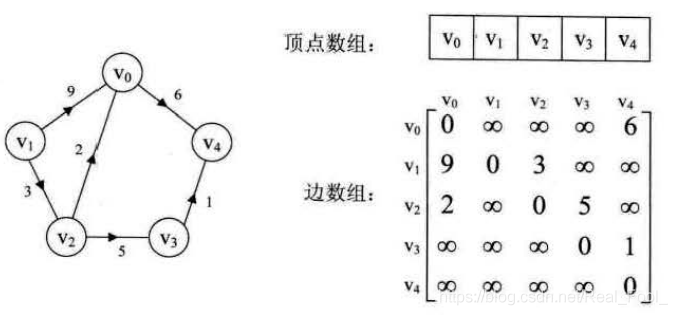
3.2 邻接表
邻接表(链表)表示由一个包含V条链表的数组Adj所构成,每个结点都有一条链表,存储与其相连的节点
无向图的邻接表的实例如下图所示

有向图的邻接表的实例如下图所示
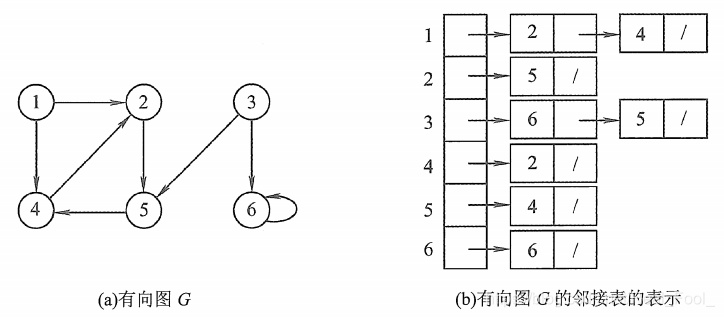
带权图的邻接表的实例如下图所示
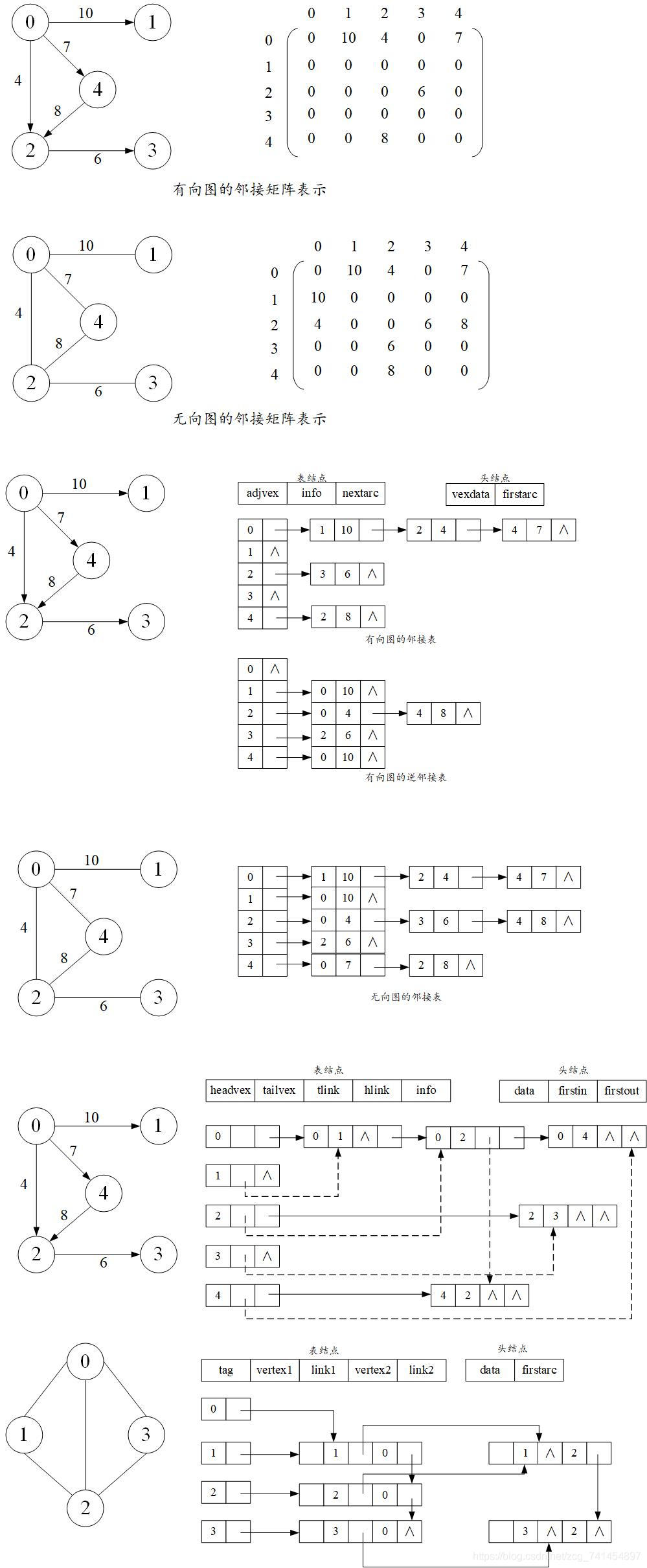
3.3 边集数组
使用一个数组来存边,数组中的每个元素都包含一条边的起点与终点(带边权的图还包含边权)。或者使用多个数组分别存起点,终点和边权。
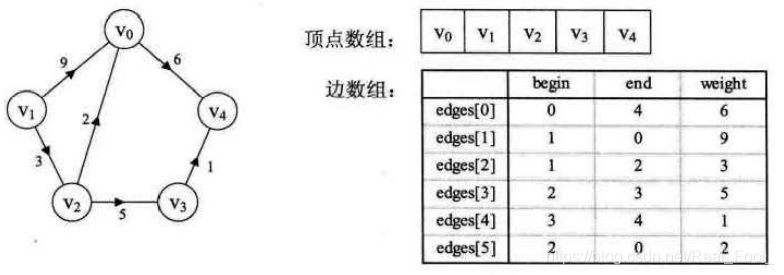
3.4 邻接多重表
邻接多重表中,无向图中的每一个顶点分配一个顶点结点,所有顶点结点构成一个顶点数组 a d j m u l t i L i s t [ n u m ] adjmultiList[num] adjmultiList[num]。另外每条边也分配一个边节点。
以下是顶点数组的展示:
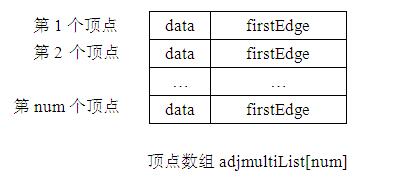
以下是边节点的展示:

以下是邻接多重表实例的展示:
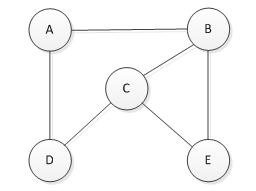
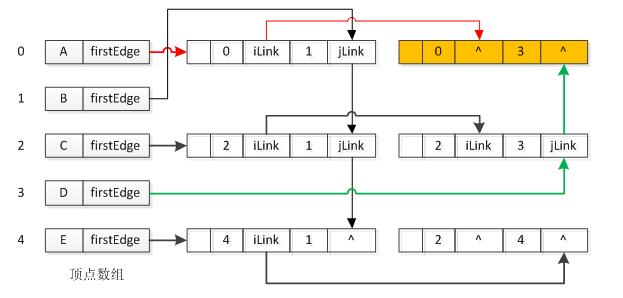
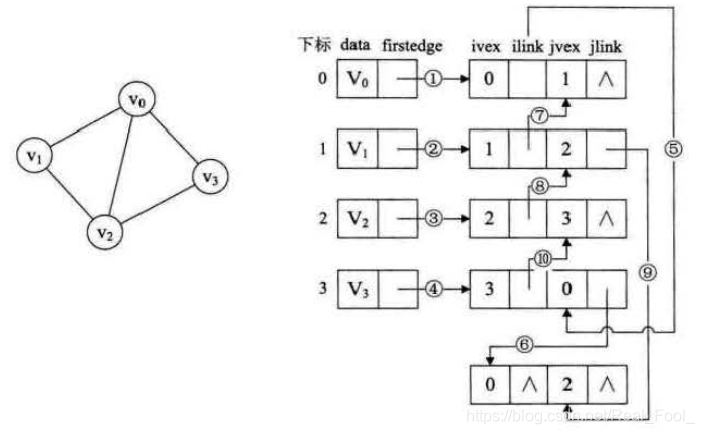
3.5 十字链表
十字链表是为了便于求得图中顶点的度(出度和入度)而提出来的。它是综合邻接表和逆邻接表形式的一种链式存储结构。其存储方式和邻接多重表类似。
以下是顶点数组的展示:
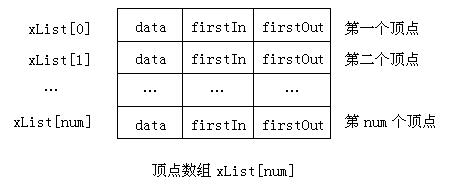
以下是边节点的展示:



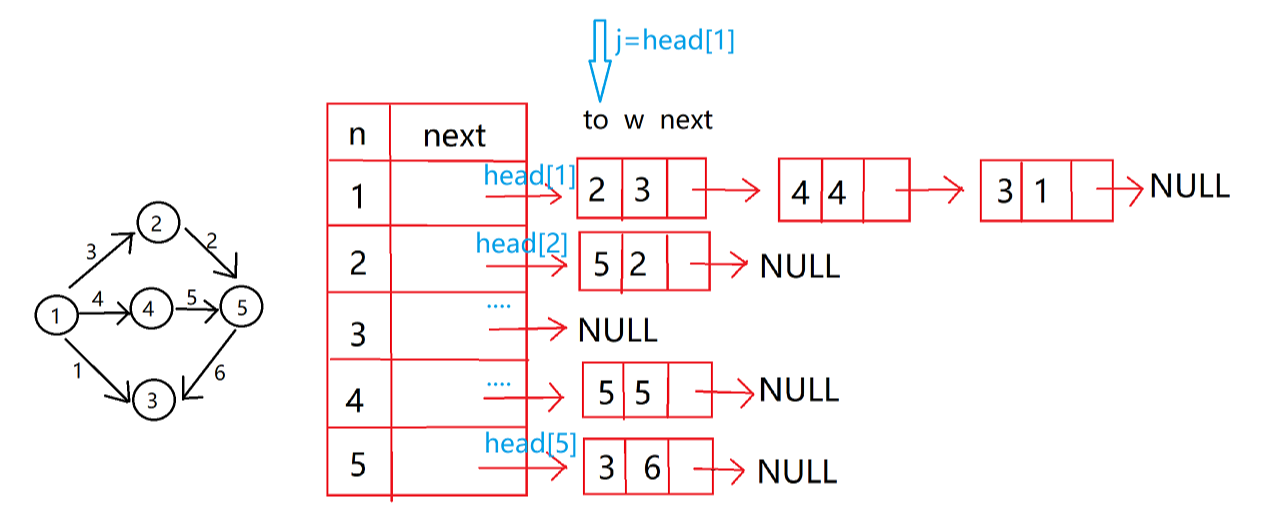
3.6 链式前向星
链式前向星是一种静态链表存储,用边集数组和邻接表相结合,可以快速访问一个顶点的所有邻接点,在算法竞赛中广泛使用。

三、图神经网络类别
目前,最先进的图神经网络分为四类,即递归图神经网络、卷积图神经网络、图自动编码器和时空图神经网络
递归图神经网络(Recurrent Graph Neural Networks, RecGNN)大多是图神经网络的先驱作品。RecGNN旨在学习具有递归神经结构的节点表示。他们假设图中的一个节点不断地与其邻居交换信息/消息,直到达到稳定的平衡,RecGNN在概念上很重要,并启发了后来对卷积图神经网络的研究。特别是,基于空间的卷积图神经网络就继承了消息传递的思想。
卷积图神经网络(Convolutional Graph Neural Networks, ConvGNNs)将卷积运算从网格数据推广到图数据。主要思想是通过聚合节点 v v v自身的特征 x v x_v xv和邻居的特征 x u x_u xu来生成节点v的表示,其中 u ∈ N ( v ) u∈N(v) u∈N(v)。与RecGNN不同,ConvGNN堆叠多个图卷积层来提取高级节点表示。ConvGNN在建立许多其他复杂的GNN模型中发挥着核心作用,可用于节点分类和图分类,如下图所示:
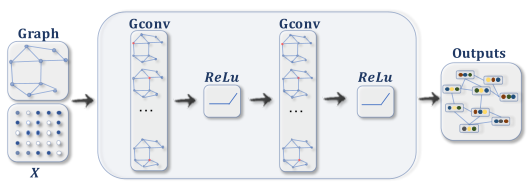
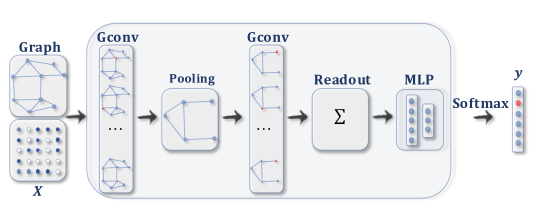
(右图)具有多个图卷积层的ConvGNN。图卷积层通过聚合来自其邻居的特征信息来封装每个节点的隐藏表示。在特征聚合之后,将非线性变换应用于结果输出。
通过堆叠多层,每个节点的最终隐藏表示从另一个邻域接收消息
(左图)图卷积层之后是池化层,以将图粗化成子图,使得粗化图上的节点表示表示表示更高的图级表示。读出层通过取子图的隐藏表示的和/均值来总结最终的图表示
图自动编码器(Graph Autoencoders, GAE)是一种无监督的学习框架,它将节点/图编码到潜在向量空间中,并根据编码的信息重建图数据。GAE用于学习网络嵌入和图生成分布。对于网络嵌入,GAE通过重构图的结构信息(如图的邻接矩阵)来学习潜在节点表示。对于图生成,一些方法一步一步地生成图的节点和边,而另一些方法一次输出图。下图展示了用于网络嵌入的GAE。
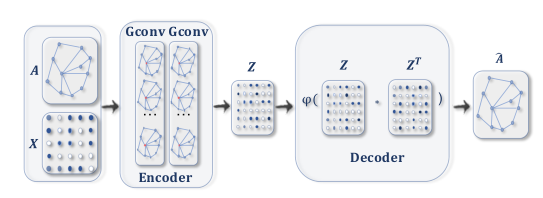
编码器使用图卷积层来获得每个节点的网络嵌入。解码器计算给定网络嵌入的成对距离。
在应用非线性激活函数之后,解码器重建图邻接矩阵。通过最小化真实邻接矩阵和重构邻接矩阵之间的差异来训练网络
时空图神经网络(Spatial-temporal Graph Neural Networks, STGNN)旨在从时空图中学习隐藏模式,这在交通速度预测、驾驶员机动预期和人类动作识别等各种应用中变得越来越重要。STGNN的关键思想是同时考虑空间依赖性和时间依赖性。当前的许多方法将图卷积与RNN或CNNs集成以捕获空间依赖性,从而对时间依赖性进行建模。下图展示了用于时空图预测的STGNN。
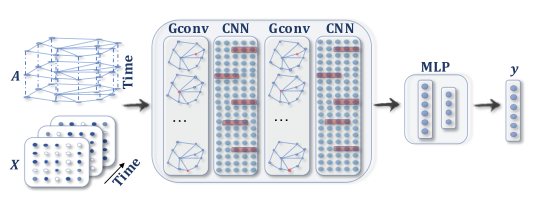
用于时空图预测的STGNN。图卷积层之后是1D-CNN层。图卷积层对A和X(t)进行运算以捕获空间相关性,而1D-CNN层沿时间轴X滑动以捕获时间相关性。
输出层是线性变换,为每个节点生成预测,例如其在下一时间步长的未来值。
相关文章:

图神经网络系列之序章
文章目录 一、为什么需要图神经网络?二、图的定义1.图的定义和种类2.一些关于图的重要概念2.1 子图2.2 连通图2.3 顶点的度、入度和出度2.4 边的权和网2.5 稠密图、稀疏图 3.图的存储结构3.1 邻接矩阵3.2 邻接表3.3 边集数组3.4 邻接多重表3.5 十字链表3.6 链式前向…...

Unity中 UI Shader的基本功能
文章目录 前言一、实现思路1、暴露一个 2D 类型的属性来接受UI的纹理2、设置shader的层级为TransParent半透明渲染层级,一般UI都是在这个渲染层级3、更改混合模式,是 UI 使用的纹理,该透明的地方透明 二、代码实现 前言 Unity中 UI Shader的…...
【自学开发之旅】Flask-标准化返回-连接数据库-分表-orm-migrate-增删改查(三)
业务逻辑不能用http状态码判断,应该有自己的逻辑判断。想要前端需要判断(好多if…else),所以需要标准化,标准化返回。 json标准化返回: 最外面:data,message,code三个字段。 data:返回的数据 co…...

numpy增删改查
NumPy是一个用于科学计算的Python库,它提供了一个多维数组对象以及许多用于操作这些数组的函数。下面是关于如何在NumPy中进行增删改查操作的一些基本示例: 创建NumPy数组: import numpy as np # 创建一个一维数组 arr np.array([1, 2, 3, …...

【kafka】kafka重要的集群参数配置
如何规划Kafka 对于实际应用的生产环境中,需要尽量先规划设计好集群,避免后期业务上线后费力调整。在考量部署方案时需要通盘考虑,不能仅从单个维度上进行评估,下面是几个重要的维度的考量和建议: 这里重点说说操作系…...

cs224w_colab3_2023 And cs224w_colab4_2023学习笔记
class GNNStack(torch.nn.Module):def __init__(self, input_dim, hidden_dim, output_dim, args, embFalse):super(GNNStack, self).__init__() #这里的继承表示参见 https://blog.csdn.net/wanzew/article/details/106993425 # 继承时运行继承类别的函数 总之 __mro__的目的…...
Cannot find module ‘prop-types‘
把这个import删了。...

LeetCode-63-不同路径Ⅱ-动态规划
题目描述: 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。 现在考虑网格中有障碍物。那…...
unity 使用Photon进行网络同步
Pun使用教程 第一步:请确保使用的 Unity 版本等于或高于 2017.4(不建议使用测试版)创建一个新项目。 第二步:打开资源商店并找到 PUN 2 资源并下载/安装它。 导入所有资源后,让 Unity 重新编译。 第三步…...

大数据课程M1——ELK的概述
文章作者邮箱:yugongshiyesina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 了解ELK的定义; ⚪ 掌握ELK的使用; 一、什么是ELK 1. 简介 ELK 是elastic公司提供的一套完整的日志收集以及展示的解决方案,是三个…...

C# byte[] 如何转换成byte*
目标:将byte[]转成byte*以方便使用memcpy [DllImport("kernel32.dll", EntryPoint "RtlCopyMemory", CharSet CharSet.Ansi)] public extern static long CopyMemory(IntPtr dest, IntPtr source, int size); private void butTemp_Click(object…...

MySQL与Oracle的分页
MySQL与Oracle的分页 当我们通过SQL去查询一个结果集的时候,并不需要查看所有行,可能只是查看前几行,或者中间的几行。则需要像MySQL的limit或Oracle的ROWNUM与FETCH NEXT来实现。 MySQL 语法 SELECT * FROM table_name LIMIT [offset,] ro…...
git基本手册
Git and GitHub for Beginners Tutorial - YouTube Kevin Stratvert git config --global user.name “xxx” git config --global user.email xxxxx.com 设置默认分支 git config --global init.default branch main git config -h查看帮助 详细帮助 git help config 清除 cl…...
每日一题(两数相加)
每日一题(两数相加) 2. 两数相加 - 力扣(LeetCode) 思路 思路: 由于链表从头开始向后存储的是低权值位的数据,所以只需要两个指针p1和p2,分别从链表的头节点开始遍历。同时创建一个新的指针new…...

恒运资本:沪指震荡涨0.28%,医药板块强势拉升,金融等板块上扬
15日早盘,沪指盘中震荡上扬,科创50指数表现强势;北向资金小幅净流入。 到午间收盘,沪指涨0.28%报3135.31点,深成指、创业板指涨均0.11%,科创50指数涨1.04%;两市合计成交4357亿元,北…...

【计算机网络】Tcp详解
文章目录 前言Tcp协议段格式TCP的可靠性面向字节流应答机制超时重传流量控制滑动窗口(重要)拥塞控制延迟应答捎带应答标志位具体标志位三次握手四次挥手粘包问题TCP异常情况listen的第二个参数 前言 前面我们学习了传输层协议Udp,今天我们一…...

最简单的laravel不使用任何扩展导出csv
php导出csv是非常常用的操作,网上也有灰常多的扩展。如果只是单纯的导出csv数据,完全没有必要去用扩展。现在做项目,都是代码能少就少,扩展能不用就不用。好了,不废话了,开干! 直接搞一个方法&…...
Android studio 断点调试、日志断点
目录 参考文章参考文章1、运行调试2、调试操作3、断点类型行断点的使用场景属性断点的使用场景异常断点的使用场景方法断点的使用场景条件断点日志断点 4、断点管理区 参考文章 参考文章 1、运行调试 开启 Debug 调试模式有两种方式: Debug Run:直接…...
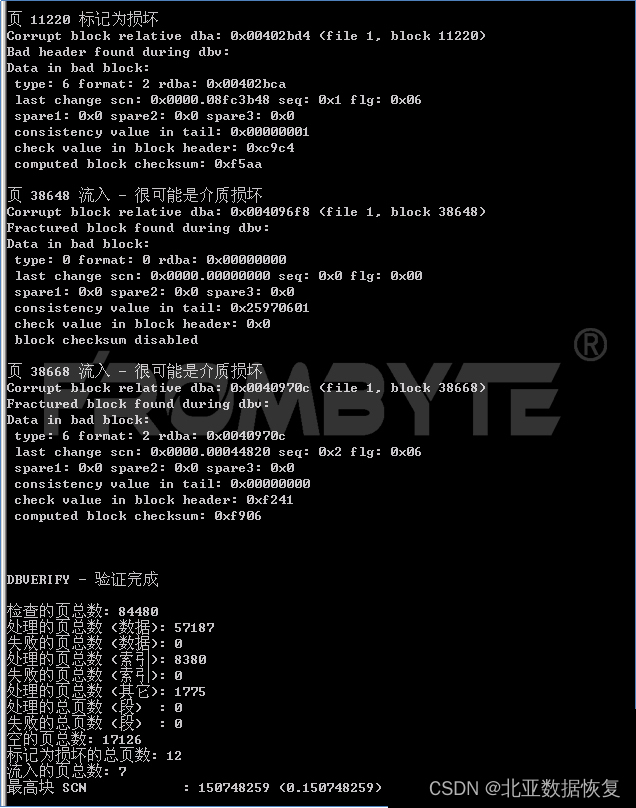
服务器数据恢复-热备盘同步过程中硬盘离线的RAID5数据恢复案例
服务器数据恢复环境: 华为OceanStor某型号存储,11块硬盘组建了一组RAID5阵列,另外1块硬盘作为热备盘使用。基于RAID5阵列的LUN分配给linux系统使用,存放Oracle数据库。 服务器故障: RAID5阵列1块硬盘由于未知原因离线…...

Python 使用input获取用户输入
视频版教程 Python3零基础7天入门实战视频教程 input()函数用于向用户生成一条提示,然后获取用户输入的内容。由于input()函数总会将用户输入的内容放入字符串中,因此用户可以输入任何内容,input()函数总是返回一个字符串。我们可以通过int(…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...
