手撕排序之堆排序
一、概念:
什么是逻辑结构、物理结构?
逻辑结构:是我们自己想象出来的,就像内存中不存在一个真正的树
物理结构(存储结构):实际上在内存中存储的形式。
堆的逻辑结构是一颗完全二叉树
堆的物理结构是一个数组
之前讲过二叉树可以用两种结构进行表示。
第一种就是链式结构,将一个一个结点进行链接。
第二种就是用数组表示。
数组表示意味着我们就是以数组为结构进行访问,但我们可以通过父子结点的下标关系将其看成树。
下面是孩子与结点的下标关系(需要记住!)
 、
、
思路:
我们将数组想象成一个完全二叉树——首先第一个表示树的根,接下来两个表示根的两个孩子,数组的下面4个表示树的两个孩子的下面一层,以此类推。最后一层不满,前面的都是连续的。
但是进行了上面的步骤后,还是不能将其称为堆。
堆分为两类:
- 大顶堆(大根堆):树中所有的父亲都大于等于孩子
- 小顶堆(小根堆):树中所有的父亲都小于等于孩子
一道经典例题(判断一串数字是否是堆)

解题方法:
将第一个数字看作二叉树的根,再往后取两个数字当作根的左右孩子,接着再取4个数,以此类推。直至还原成一个完全二叉树,接着看是不是属于堆的两种类型,如果既不是大顶堆,也不是小顶堆,那么这一串数字就不是堆。

堆的插入:
首先堆在逻辑结构上是一颗二叉树,但逻辑结构是我们自己想象出来的,本质上数据还是存储在数组中,所以我们应该对数组进行修改。
这里的插入我们选择尾插,尾插后有一下几种情况:
1、

直接尾插,不用改变任何顺序
2、
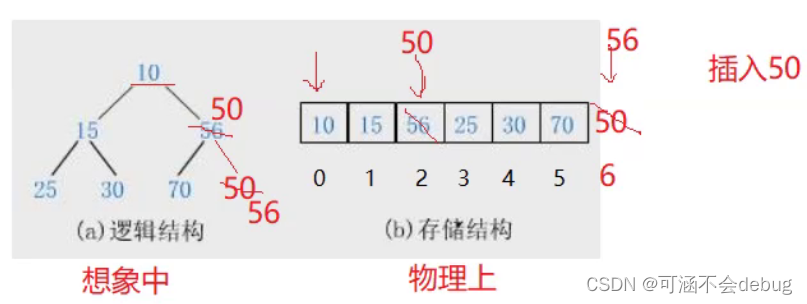
发现尾插顺序不满足大堆或者小堆,记住插入只影响自己的祖先,与其他的祖先没有关系!
所以我们只要改变孩子与祖先的关系,如何根据孩子找到父亲的下标呢?
parent = (child-1)/ 2 即可。
将这两个位置进行交换。
3、最坏的情况
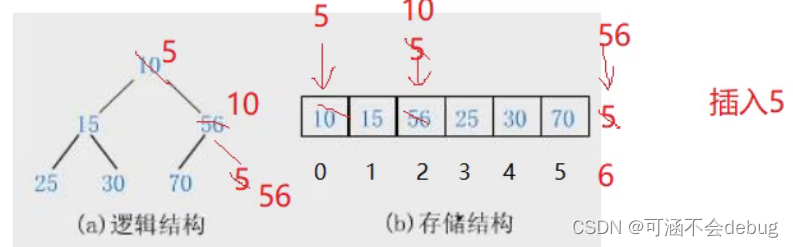
最坏情况下可能会一直到根节点
因此每次交换完,都要进行孩子与父亲的比较。
时间复杂度:
我们看最坏的情况,执行次数就是树的高度次,也就是O(logN).
原码:
Swap(HeapDataType* a, HeapDataType* b)
{HeapDataType tmp = *a;*a = *b;*b = tmp;
}void AdujstUp(HeapDataType* a,int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}elsebreak;}
}void HeapPush(HP* php,HeapDataType x)
{assert(php);//判断是否需要扩容if (php->capcity == php->size){int newCapcity = php->capcity == 0 ? 4 : php->capcity * 2;//注意realloc的使用方法HeapDataType* tmp = (HeapDataType*)realloc(php->a, sizeof(HeapDataType) * newCapcity);if (tmp == NULL){perror(realloc);exit(-1);}php->a = tmp;php->capcity = newCapcity;}php->a[php->size] = x;php->size++;//向上调整算法,跟祖先进行比较AdujstUp(php->a, php->size-1);
}
堆的删除:
首先我们需要明确针对堆的删除,我们需要删除的是堆的根节点。
思路一(错误)
我们直接将数组的首元素删除,然后移动(memmove)后面的数据内容,但这样极大可能影响了大小堆的结构!
思路二:(向下调整算法)
我们直接将数组的首元素和数组的最后一个元素交换位置,然后size--,删除最后一个元素,也就是根节点。
这时候我们发现根节点的左右子树都是大堆/小堆
然后将根节点与左右节点的较小结点进行比较,如果还小,那么继续交换,直到叶节点为止
以此类推,堆顶的元素是最小的,继续pop,那么次小的元素又到堆顶……
原码:
void AjustDown(HeapDataType* a,int n,int parent)
{int child = parent * 2 + 1;while (child < n){//确定最小孩子if (child + 1 < n && a[child] < a[child + 1])//防止只有左叶子,访问右叶子会越界child++;if (a[parent] < a[child]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}elsebreak;}
}void HeapPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AjustDown(php->a,php->size,0);
}
小总结:(调整算法的前提)
向上调整算法的前提是:前面的数据内容都是大堆/小堆
向下调整算法的前提是:左右子树的数据内容都是大堆/小堆
TIP:
我们可以根据这个思路,可以实现一个排序算法,也就是堆排序。
时间复杂度:
跟插入一样,都是O(logN)。
堆排序:
1、建堆:
我们可以直接用向上寻找算法进行建堆。——为什么?
建堆有两种方式:
第一种就是向上建堆。
利用向上调整算法,每一个插入然后进行向上调整,完成建堆
时间复杂度:O(N) = N*logN
解析:


我们采取最差情况,得到O(h)的表达式,然后再用等式将h替换成n
总体的时间复杂度是O(N) = N*logN
第二种就是向下建堆。
从倒数第一个非叶子结点开始跳(也就是最后一个结点的父亲)
时间复杂度:O(N)
解析:
先假设h是树的高度,N是结点的个数
我们先用树的高度h作为自变量便于计算。最后再用等式进行替换。
考虑最坏的情况:
每层数据的个数 * 向下移动的层数
然后是等差*等比的数列求和,我们采用错位相减法计算。


最后的计算结果是2^h - 1- h.
因为2^h - 1 = n.
所以O(N) = N - log(N+1)
为什么向下调整算法要比向上调整复杂度低呢?
因为向下调整层数越低,向下调整的次数越多,所以是低*高
而向上调整层数越高,向上调整的次数就越多,所以是高*高,并且层数越高,占比越大,最后一层的结点个数就占了50%。
最后一层结点个数多并且向上调整的次数也多!
2、排序
如果我们排升序,建大堆。
排降序,建小堆。
原因:
建小堆有可能关系全乱了,剩下数据,看成新的完全二叉树,不一定是堆,重新建堆代价太大!
例子:
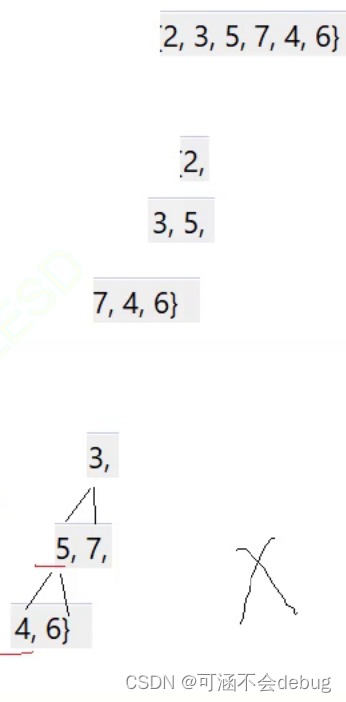
建大堆:
堆顶跟最后一个位置交换,最大的数据排好了,然后将最后一个元素不列入排序,剩下元素除了根节点其余是堆。剩下的数据由堆顶元素进行向下调整算法,选出次大的,代价是logN。
注意向上调整算法和向下调整算法的前提都是保证数据是堆!
以下是建小堆的堆排序算法
所以一共的时间复杂度O(N) = N*logN.
原码:
void HeapSort(int* a, int n)
{//建堆//建小堆/大堆//向上调整建堆//O(N*logN)/*for (int i = 1; i < n; i++){AdujstUp(a, i);}*///向下调整建堆//O(N),效率比向上调整高for (int i = (n - 1 - 1) / 2; i >= 0; i--)//注意这里的n是数据个数,而公式中的n是下标{AjustDown(a, n, i);}//根节点的值要么最大,要么最小,可以进行排序//这一部分的时间复杂度O(N) = N*logNint end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AjustDown(a, end, 0);end--;}
}相关文章:

手撕排序之堆排序
一、概念: 什么是逻辑结构、物理结构? 逻辑结构:是我们自己想象出来的,就像内存中不存在一个真正的树 物理结构(存储结构):实际上在内存中存储的形式。 堆的逻辑结构是一颗完全二叉树 堆的物理结构是一个数组 之…...

【奇想星球】重磅!我们的AIGC共创社区平台上线了!
文章目录 01 前言功能模块 02 相识缘起连接价值平台优势 03 奇想星球04 我们做了什么时间线 05 初心愿景06 可爱的小伙伴们后续开发及招募计划 07 结语 公众号原文链接 01 前言 2023年9月10日,我们的平台网站上线了! 奇想星球 | AIGC共创社区平台。网站地…...

2023年数维杯数学建模B题节能列车运行控制优化策略求解全过程文档及程序
2023年数维杯数学建模 B题 节能列车运行控制优化策略 原题再现: 在城市交通电气化进程快速推进的同时,与之相应的能耗增长和负面效应也在迅速增加。城市轨道交通中的快速增长的能耗给城轨交通的可持续性发展带来负担。2018 年,北京、上海、…...

Python--测试代码
目录 1、使用pip安装pytest 1.1 更新pip 1.2 安装putest 2、测试函数 2.1 单元测试和测试用例 2.2 可通过的测试 2.3 运行测试 2.4 未通过的测试 2.5 解决测试未通过 2.6 添加新测试 3、测试类 3.1 各种断言 3.2 一个测试的类 3.3 测试AnonymousSurvey类 3.4 使…...

CentOS 系列版本搭建 Nginx 服务
目录 Nginx 介绍 Nginx 安装 CentOS 系列版本 Nginx 删除 CentOS 系列版本 Nginx 介绍 Nginx 是一个广泛使用的Web服务器和反向代理服务器。 反向代理和负载均衡:Nginx支持反向代理和负载均衡,能够分发请求到多个后端服务器,提高了可用性…...
)
目标检测YOLO实战应用案例100讲-基于机器视觉的输电线路小目标检测和缺 陷识别(下)
目录 3.3.1 输电线路所有尺寸目标检测性能对比 3.3.2 输电线路小目标检测性能对比...

argparse--命令行参数解析库
文章目录 位置参数help ->描述信息type -> 被转换的类型 可选参数action ->动作基本类型 (store_true)短选项 结合位置参数和可选参数choiceaction ->动作基本类型 (count)default -> 默认值 argparse模块使编写用户友好的命令行变得容易 接口。程序定义了它需要…...
elasticsearch4-文档操作
个人名片: 博主:酒徒ᝰ. 个人简介:沉醉在酒中,借着一股酒劲,去拼搏一个未来。 本篇励志:三人行,必有我师焉。 本项目基于B站黑马程序员Java《SpringCloud微服务技术栈》,SpringCloud…...
阿里云服务器上CentOS 7.6使用rpm包安装MySQL 8.0.31
我这里下载的是最新版本,需要到MySQL官网最新版本下载地址。 要是想要下载以前的版本需要到MySQL以前版本网址中。 1)先使用wget https://cdn.mysql.com//Downloads/MySQL-8.0/mysql-8.0.31-1.el7.x86_64.rpm-bundle.tar(这个网址现在已经不…...

redis未授权漏洞
redis未授权漏洞是什么? Redis 默认情况下会绑定在 0.0.0.0:6379,这样将会将 Redis 服务暴露到公网上,如果在没有开启认证的情况下,可以导致任意用户在可以访问目标服务器的情况下未授权访问Redis以及读取 Redis的数据 它有什么危…...

详解3dMax中渲染线框的两种简单方法
在3dMax中渲染线框是你在某个时候想要完成的事情,例如为了演示分解步骤,或是仅仅为了在模型上创建线框覆盖的独特效果。为三维模型渲染线框最常见的原因是能够在模型上显示干净的拓扑。这篇文章将带你了解在3dMax中渲染三维模型线框的两种最常见、最简单…...

Git - Git 工作流程
文章目录 Git WorkFlow图解小结 Git WorkFlow Git Flow是一种基于Git的工作流程,确实利用了Git作为分布式版本控制系统的优势。 本地代码库 (Local Repository): 每个开发者都维护自己的本地代码库,这是Git分布式性质的体现。本地代码库包含了完整的项目…...
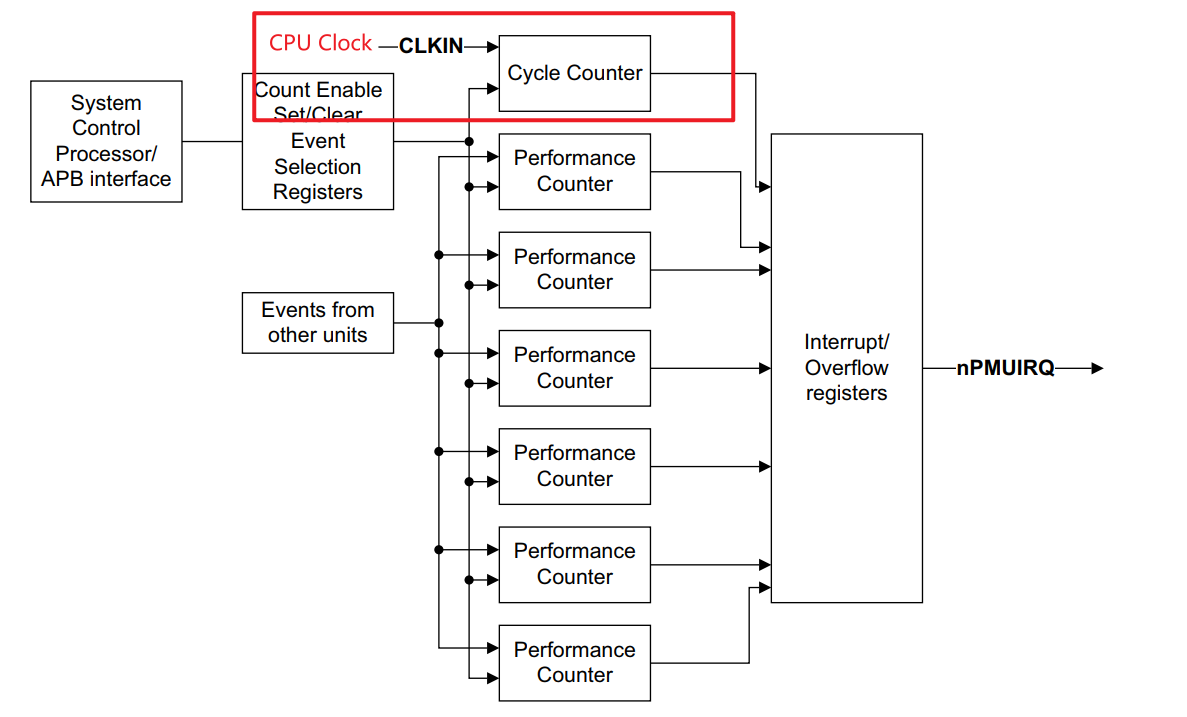
ARM如何利用PMU的Cycle Counter(时钟周期)来计算出CPU的时钟频率
本章将学习如何利用ARM PMU的Cycle Counter,来计算出CPU的时钟周期,从而计算出CPU的时钟频率。在介绍计算方法前,有必要先介绍下什么是时钟周期、机器周期以及指令周期。 如何计算出CPU的时钟频率 一,时钟周期,机器周…...
56资源网系统源码搭建知识付费-含源码
内置了上万条数据资源 大致功能: 支持免费与付费(增加了插件付费插件)支持侧边栏支持添加各类型广告(你所能用到的基本都有).支持网盘下载模块支持所有页面自定义支持文章页三方跳转支持添加页面支持自定义采集&#…...

【运营版】仿东郊到家上门服务app小程序开发同城美容家政预约推拿足浴SPA技师派单源码
套餐一:源码=小程序端+公众号端+APP端=280元 套餐二:全包服务 包服务器+域名+APP+认证小程序+H5+PC=1000元 后端:系统后端使用PHP语言开发 前端:前端使用uniapp进行前后端分离开发 用户端功能模块:技师选择 预约服务 优惠券 订单 技师服务...
使用websocket实现简易聊天室)
uniapp项目实践总结(十五)使用websocket实现简易聊天室
导语:在一些社交软件中,经常可以看到各种聊天室的界面,接下来就总结一下聊天室的原理个实现方法,最后做一个简易的聊天室,包括登录/登出、加入/离开房间、发送接收聊天消息等功能。 目录 准备工作原理分析组件实现实战演练服务端搭建案例展示准备工作 在pages/index文件夹…...

论文阅读之Learning and Generalization of Motor Skills by Learning from Demonstration
论文阅读其实就是用自己的话讲一遍,然后理解其中的方法 0、论文基本信息 为什么阅读此篇论文:因为它是DMP经典论文,被引多次,学史可以明智,了解最初机理。 论文题目:Learning and Generalization of Moto…...

SpringCloud中的Eureka的集群配置
微服务框架中最为重要的就是注册中心,如果只是单注册中心,一旦出现问题,容易导致整个微服务环境不可用,所以建议注册中心集群。 目前SpringCloud框架中使用Eureka作为注册中心,本文简单介绍一下Eureka的集群配置&…...
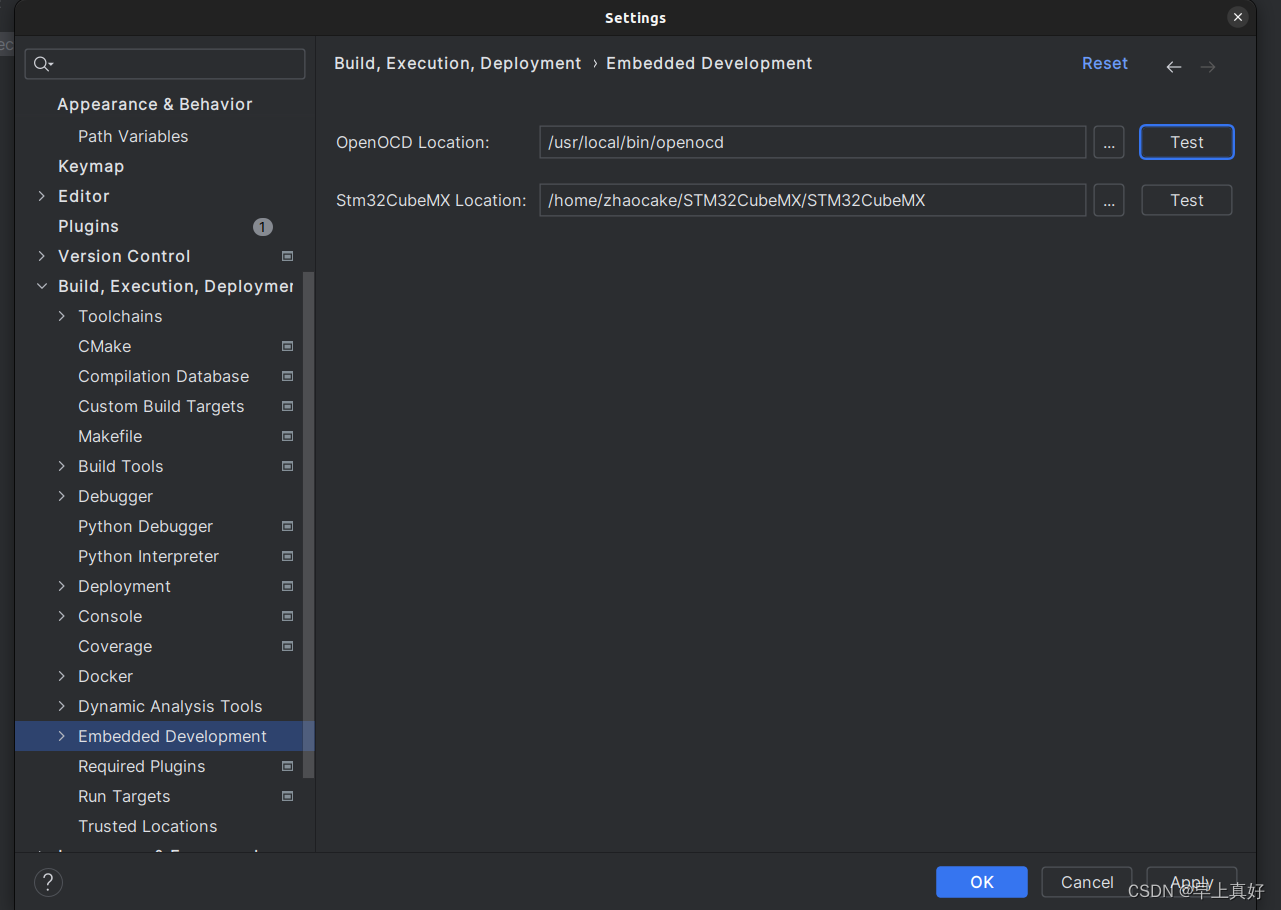
10 Ubuntu下配置STMCubeMX与CLion IDE联合环境搭建(不包含下载CLion的教程)
序言 果然作为一名测控系的学生,纯搞视觉多少还是有点与专业脱节,决定入坑嵌入式。选择STM32进行入门,并且使用CubeMX加CLion作为我的第一个真正意义上的嵌入式开发环境(大一的时候玩过一段时间,但是没什么技术&#…...

负载均衡原理及应用
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
