【力扣周赛】第 363 场周赛(完全平方数和质因数分解)
文章目录
- 竞赛链接
- Q1:100031. 计算 K 置位下标对应元素的和
- 竞赛时代码
- 写法2——手写二进制中1的数量
- Q2:100040. 让所有学生保持开心的分组方法数(排序后枚举分界)
- 竞赛时代码
- Q3:100033. 最大合金数(二分答案)
- 竞赛时代码
- Q4:8041. 完全子集的最大元素和
- 竞赛时代码——质因数分解+哈希表
- 解法2——定义core(x)为 x 除去完全平方因子后的剩余结果
- 成绩记录
竞赛链接
https://leetcode.cn/contest/weekly-contest-363/
Q1:100031. 计算 K 置位下标对应元素的和
https://leetcode.cn/problems/sum-of-values-at-indices-with-k-set-bits/
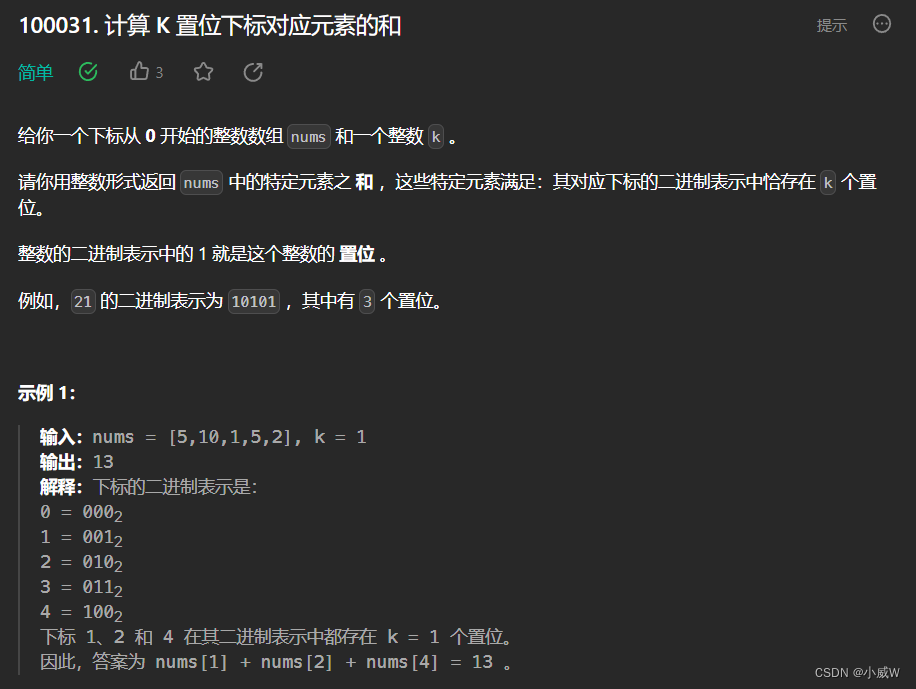
提示:
1 <= nums.length <= 1000
1 <= nums[i] <= 10^5
0 <= k <= 10
竞赛时代码
class Solution {public int sumIndicesWithKSetBits(List<Integer> nums, int k) {int ans = 0;for (int i = 0; i < nums.size(); ++i) {if (Integer.bitCount(i) == k) ans += nums.get(i);}return ans;}
}
写法2——手写二进制中1的数量
class Solution {public int sumIndicesWithKSetBits(List<Integer> nums, int k) {int ans = 0;for (int i = 0; i < nums.size(); ++i) {if (cnt(i) == k) ans += nums.get(i);}return ans;}public int cnt(int x) {int res = 0;while (x != 0) {res++;x &= x - 1;}return res;}
}
Q2:100040. 让所有学生保持开心的分组方法数(排序后枚举分界)
https://leetcode.cn/problems/happy-students/description/
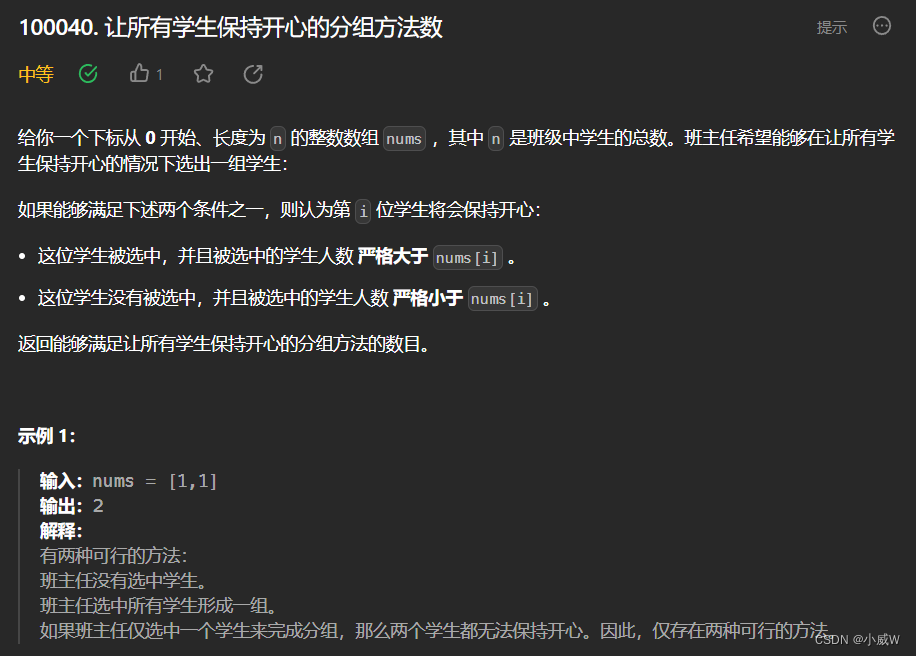
提示:
1 <= nums.length <= 10^5
0 <= nums[i] < nums.length
竞赛时代码
将学生排序后, 一个学生 x 被选了的时候,比它小的一定必须被选;同理一个学生 y 不被选的时候,比它大的一定不能被选。
枚举每个位置,假设 0~i 被选择,i+1~n-1 不被选择。检查是否合理,合理则 ans ++;
class Solution {public int countWays(List<Integer> nums) {// 按题意——一定先选择nums值更小的学生,所以——从小到大排序Collections.sort(nums);int n = nums.size(), ans = 0;if (nums.get(0) > 0) ans++; // 处理特例是否可以全不选// 枚举选择到每个位置for (int i = 0; i < n; ++i) { // 检查已经选择人数i+1是否严格大于nums[i]if (i + 1 > nums.get(i)) { // 检查已经选择人数i+1是否严格小于下一个没被选择的学生nums[i+1] (注意要判断越界)if (i + 1 < n && nums.get(i + 1) <= i + 1) continue; // 不满足就跳过ans++; // 这个位置合理,答案+1}}return ans;}
}
Q3:100033. 最大合金数(二分答案)
https://leetcode.cn/problems/maximum-number-of-alloys/description/
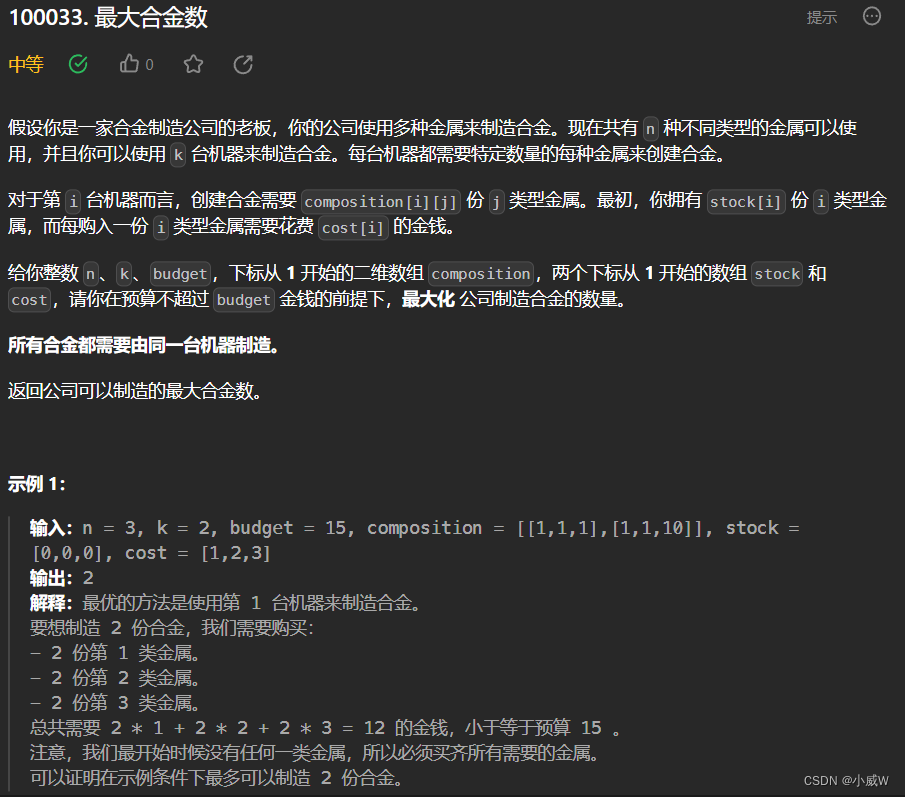
提示:
1 <= n, k <= 100
0 <= budget <= 10^8
composition.length == k
composition[i].length == n
1 <= composition[i][j] <= 100
stock.length == cost.length == n
0 <= stock[i] <= 10^8
1 <= cost[i] <= 100
竞赛时代码
注意到题目中说明——“所有合金都需要由同一台机器制造。”,且观察到 k 的数据范围较小,所以可以枚举使用每台机器。
对于每台机器,使用二分查找求出它可以制造出的最大的合金数量。
二分查找时判断的依据是花费的前有没有在 budget 的范围内。
class Solution {public int maxNumberOfAlloys(int n, int k, int budget, List<List<Integer>> composition, List<Integer> stock, List<Integer> cost) {long ans = 0;// 按照题意,所有合金都需要由同一台机器制造。枚举每个机器。for (int i = 0; i < k; ++i) {ans = Math.max(ans, op(n, budget, composition.get(i), stock, cost));}return (int)ans;}// 计算使用某台机器时的最大制造数量public long op(int n, int budget, List<Integer> composition, List<Integer> stock, List<Integer> cost) {// 二分答案long l = 0, r = (long)Integer.MAX_VALUE;while (l < r) {long mid = l + r + 1 >> 1;if (check(mid, n, budget, composition, stock, cost)) l = mid;else r = mid - 1;}return l;}// 检查是否可以造出 k 个合金public boolean check(long k, int n, int budget, List<Integer> composition, List<Integer> stock, List<Integer> cost) {long s = 0; // 记录额外花费for (int i = 0; i < n; ++i) {long need = k * composition.get(i);if (need <= stock.get(i)) continue;s += cost.get(i) * (need - stock.get(i));if (s > budget) return false; // 额外花费超了,不能造出k个合金}return true;}
}
Q4:8041. 完全子集的最大元素和
https://leetcode.cn/problems/maximum-element-sum-of-a-complete-subset-of-indices/description/

提示:
1 <= n == nums.length <= 10^4
1 <= nums[i] <= 10^9
竞赛时代码——质因数分解+哈希表
对每个下标质因数分解,两两相乘之后的结果是完全平方数,那么这两个数字的质因数分解的奇偶性相同。 例如2=21,8=23;相同质因数出现的次数的奇偶性相同,则两者可以匹配。
根据质因数分解的结果将所有数字分组即可。
class Solution {public long maximumSum(List<Integer> nums) {// 两两之间相乘之后是完全平方数,则质因数分解结果满足各个质因数数量奇偶性相同int n = nums.size();String[] mask = new String[n];long ans = 0;// key是mask,value是sumMap<String, Long> m = new HashMap<>(); for (int i = 1; i <= n; ++i) {mask[i - 1] = op(i); // 计算maskm.merge(mask[i - 1], (long)nums.get(i - 1), Long::sum); // 求和ans = Math.max(ans, m.get(mask[i - 1])); // 更新答案}return ans;}// 计算下标x的质因数分解掩码maskpublic String op(int x) {// 将质因数的数量为奇数的部分记录下来String mask = "";for (int i = 2; i <= x / i; ++i) {if (x % i == 0) {int s = 0;while (x % i == 0) {s++;x /= i;}if (s % 2 == 1) mask += String.valueOf(i) + " ";}}if (x > 1) mask += String.valueOf(x) + " ";return mask;}
}
解法2——定义core(x)为 x 除去完全平方因子后的剩余结果
https://leetcode.cn/problems/maximum-element-sum-of-a-complete-subset-of-indices/solutions/2446037/an-zhao-corei-fen-zu-pythonjavacgo-by-en-i6nu/
计算方式同质因数分解,把 n 的所有出现次数为奇数的质因子相乘,即为 core(n)。
class Solution {public long maximumSum(List<Integer> nums) {// 两两之间相乘之后是完全平方数,则质因数分解结果满足各个质因数数量奇偶性相同int n = nums.size();long[] sum = new long[n + 1];long ans = 0;for (int i = 1; i <= n; ++i) {int c = op(i); // 计算masksum[c] += nums.get(i - 1); // 求和ans = Math.max(ans, sum[c]); // 更新答案}return ans;}// 计算下标x的质因数分解掩码maskpublic int op(int x) {// 将质因数的数量为奇数的部分记录下来int res = 1;for (int i = 2; i <= x / i; ++i) {if (x % i == 0) {int s = 0;while (x % i == 0) {s++;x /= i;}if (s % 2 == 1) res *= i;}}if (x > 1) res *= x;return res;}
}
成绩记录

T4 没有那么难!想得慢了!
相关文章:

【力扣周赛】第 363 场周赛(完全平方数和质因数分解)
文章目录 竞赛链接Q1:100031. 计算 K 置位下标对应元素的和竞赛时代码写法2——手写二进制中1的数量 Q2:100040. 让所有学生保持开心的分组方法数(排序后枚举分界)竞赛时代码 Q3:100033. 最大合金数(二分答…...
RocketMQ的介绍和环境搭建
一、介绍 我也不知道是啥,知道有什么用、怎么用就行了,说到mq(MessageQueue)就是消息队列,队列是先进先出的一种数据结构,但是RocketMQ不一定是这样,简单的理解一下,就是临时存储的…...

【web开发】7、Django(2)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 一、部门列表二、部门管理(增删改)三、用户管理过渡到modelform组件四、modelform实例:靓号操作五、自定义分页组件六、datepick…...
Prometheus+Grafana可视化监控【Nginx状态】
文章目录 一、安装Docker二、安装Nginx(Docker容器方式)三、安装Prometheus四、安装Grafana五、Pronetheus和Grafana相关联六、安装nginx_exporter七、Grafana添加Nginx监控模板 一、安装Docker 注意:我这里使用之前写好脚本进行安装Docker,如果已经有D…...

R 语言的安装教程
一、下载相关软件 1、R 下载 官网:R: The R Project for Statistical Computing 找到中国镜像,下载快 历史版本点击这里 2、Rtools 下载 进入镜像后,点击这里 然后选择与上面下载的R版本相对应的版本即可 3、Rstudio 下载 官网࿱…...
uniapp-提现功能(demo)
页面布局 提现页面 有一个输入框 一个提现按钮 一段提现全部的文字 首先用v-model 和data内的数据双向绑定 输入框逻辑分析 输入框的逻辑 为了符合日常输出 所以要对输入框加一些条件限制 因为是提现 所以对输入的字符做筛选,只允许出现小数点和数字 这里用正则实现的小数点…...
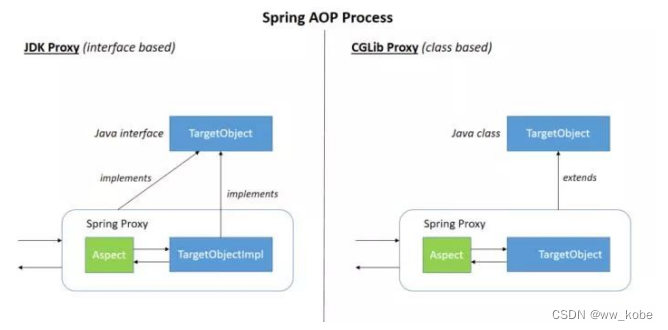
Spring 篇
1、什么是 Spring? Spring是一个轻量级的IOC和AOP容器框架。是为Java应用程序提供基础性服务的一套框架,目的是用于简化企业应用程序的开发,它使得开发者只需要关心业务需求。常见的配置方式有三种:基于XML的配置、基于注解的配置…...
three.js简单3D图形的使用
npm init vitelatest //创建一个vite的脚手架 选择 Vanilla 之后自己处理一下 在main.js中写入 // 导入three.js import * as THREE from three// 创建场景 const scene new THREE.Scene();// 创建相机 const camera new THREE.PerspectiveCamera(45, //视角window.inner…...
)
spark withColumn的使用(笔记)
目录 前言: spark withColumn的语法及使用: 准备源数据演示: 完整实例代码: 前言: withColumn():是Apache Spark中用于DataFrame操作的函数之一,它的作用是在DataFrame中添加或替换列ÿ…...
PTA:7-1 线性表的合并
线性表的合并 题目输入样例输出样例 代码解析 题目 输入样例 4 7 5 3 11 3 2 6 3输出样例 7 5 3 11 2 6 代码 #include<iostream> #include<vector> using namespace std;bool checkrep(const vector<int>& arr, int x) {for (int element : arr) {i…...

Spring 的创建和日志框架的整合
目录 一、第一个 Spring 项目 1、配置环境 2、Spring 的 jar 包 Maven 项目导入 jar 包和设置国内源的方法: 3、Spring 的配置文件 4、Spring 的核心 API ApplicationContext 4、程序开发 5、细节分析 (1)名词解释 (2&…...

11-集合和学生管理系统
1.ArrayList 集合和数组的优势对比: 长度可变添加数据的时候不需要考虑索引,默认将数据添加到末尾 1.1 ArrayList类概述 什么是集合 提供一种存储空间可变的存储模型,存储的数据容量可以发生改变 ArrayList集合的特点 长度可以变化…...

C语言进阶指针(3) ——qsort的实现
大家好,我们今天来学习回调函数qsort的实现。 首先让我们打开cplusplus.com找到qsort函数。 我们看到这个函数就可以看到它的头文件和参数信息。 #include<stdlib.h> void qsort (void* base, size_t num, size_t size, int (*compar)(const void*,const voi…...

Rust源码分析——Rc 和 Weak 源码详解
Rc 和 Weak 源码详解 一个值需要被多个所有者拥有 rust中所有权机制在图这种数据结构中,一个节点可能被多个其它节点所指向。那么如何表示图这种数据结构?在多线程中,多个线程可能会持有同一个数据?如何解决这个问题。 Rc rus…...
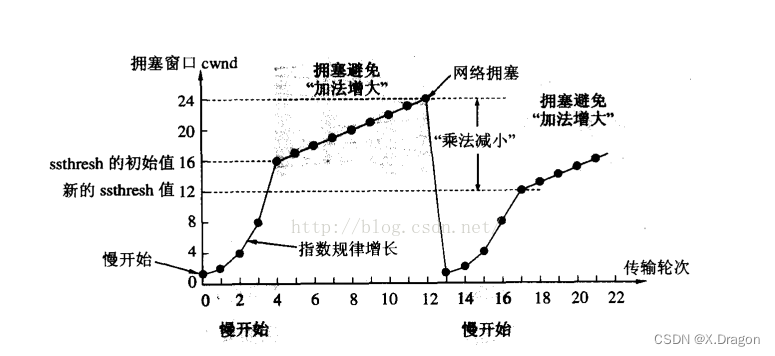
【网络编程】深入理解TCP协议二(连接管理机制、WAIT_TIME、滑动窗口、流量控制、拥塞控制)
TCP协议 1.连接管理机制2.再谈WAIT_TIME状态2.1理解WAIT_TIME状态2.2解决TIME_WAIT状态引起的bind失败的方法2.3监听套接字listen第二个参数介绍 3.滑动窗口3.1介绍3.2丢包情况分析 4.流量控制5.拥塞控制5.1介绍5.2慢启动 6.捎带应答、延时应答 1.连接管理机制 正常情况下&…...

社区团购商城小程序v18.1开源独立版+前端
新增后台清理缓存功能 修复定位权限 修复无法删除手机端管理员 11月新登录接口修复! 修复商家付款到零钱, 修复会员登陆不显示头像, 修复无法修改会员开添加绑定...
MATLAB入门-字符串操作
MATLAB入门-字符串操作 注:本篇文章是学习笔记,课程链接是:link MATLAB中的字符串特性: 无论是字符还是字符串,都要使用单引号来‘’表示;在MATLAB中,字符都是在矩阵中存储的,无论…...

Kong Learning
一、Kong Kong是由Mashape公司开源的可扩展的Api GateWay项目。它运行在调用Api之前,以插件的扩展方式为Api提供了管理。比如,鉴权、限流、监控、健康检查等,Kong是基于lua语言、nginx以及openResty开发的,所有拥有动态路由、负载…...

Python怎样写桌面程序
要编写Python桌面应用程序,可以使用以下几种方法: 1.使用Tkinter模块:Tkinter是Python自带的GUI工具包之一,可以使用它来创建基本的GUI界面。例如,可以创建一个简单的窗口,添加按钮、文本框等控件…...

蓝桥杯2023年第十四届省赛真题-平方差--题解
蓝桥杯2023年第十四届省赛真题-平方差 时间限制: 3s 内存限制: 320MB 提交: 2379 解决: 469 题目描述 给定 L, R,问 L ≤ x ≤ R 中有多少个数 x 满足存在整数 y,z 使得 x y2 − z2。 输入格式 输入一行包含两个整数 L, R,用一个空格分隔。 输出格…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...
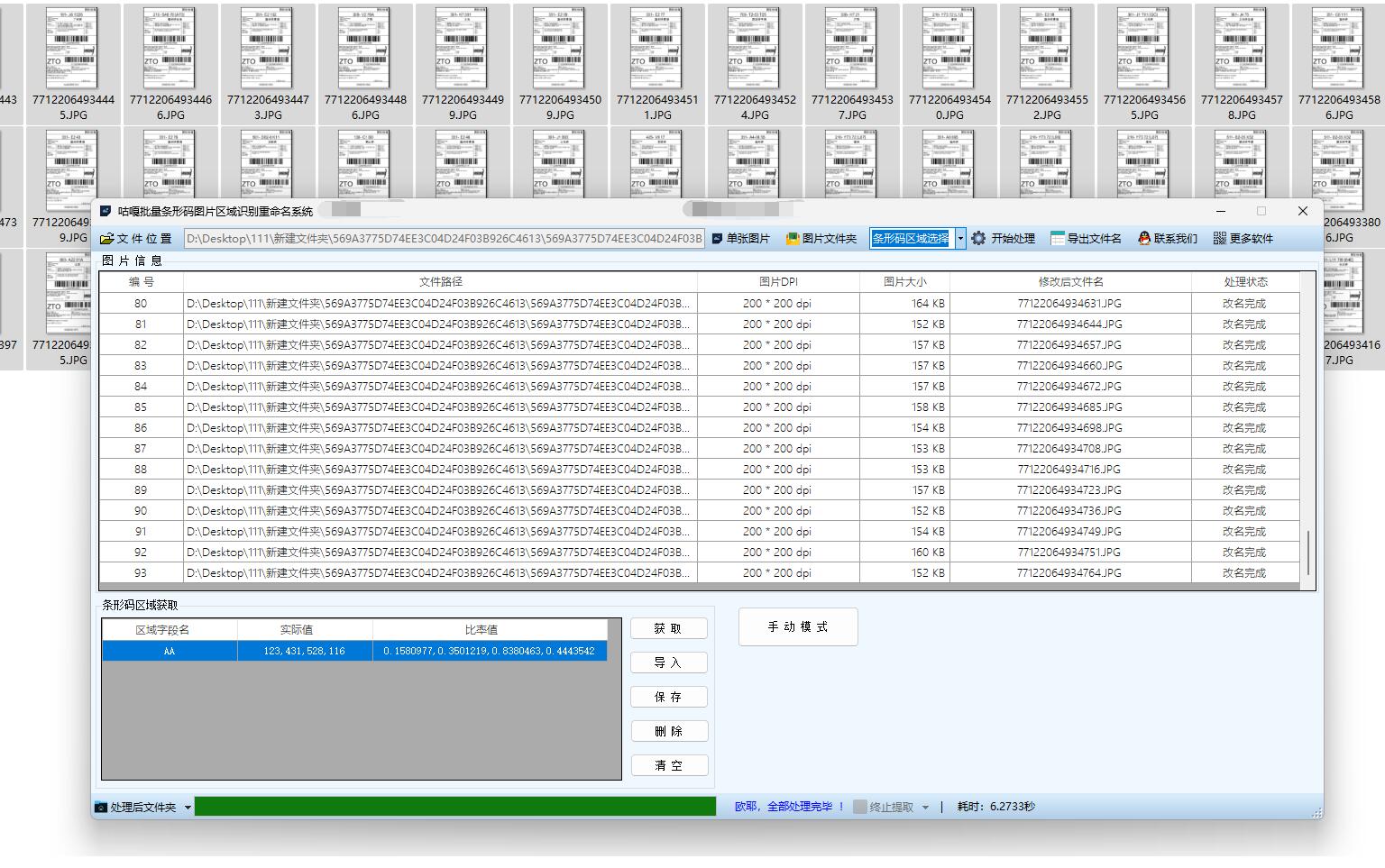
【工具教程】多个条形码识别用条码内容对图片重命名,批量PDF条形码识别后用条码内容批量改名,使用教程及注意事项
一、条形码识别改名使用教程 打开软件并选择处理模式:打开软件后,根据要处理的文件类型,选择 “图片识别模式” 或 “PDF 识别模式”。如果是处理包含条形码的 PDF 文件,就选择 “PDF 识别模式”;若是处理图片文件&…...

联邦学习带宽资源分配
带宽资源分配是指在网络中如何合理分配有限的带宽资源,以满足各个通信任务和用户的需求,尤其是在多用户共享带宽的情况下,如何确保各个设备或用户的通信需求得到高效且公平的满足。带宽是网络中的一个重要资源,通常指的是单位时间…...

生产管理系统开发:专业软件开发公司的实践与思考
生产管理系统开发的关键点 在当前制造业智能化升级的转型背景下,生产管理系统开发正逐步成为企业优化生产流程的重要技术手段。不同行业、不同规模的企业在推进生产管理数字化转型过程中,面临的挑战存在显著差异。本文结合具体实践案例,分析…...
