Java手写拓扑排序和拓扑排序应用拓展案例
Java手写拓扑排序和拓扑排序应用拓展案例
1. 算法思维导图
2. 该算法的手写必要性和市场调查
拓扑排序是一种常用的图算法,广泛应用于任务调度、编译器优化、依赖关系分析等领域。手写拓扑排序算法的必要性在于加深对该算法的理解,并能够根据具体需求进行灵活的定制和优化。市场调查显示,拓扑排序算法在软件开发和数据处理领域有着广泛的应用需求,对该算法的手写实现和优化能力有很高的市场价值。
3. 该算法的详细介绍和步骤
拓扑排序是一种基于有向无环图(DAG)的排序算法,通过对图中节点的依赖关系进行排序,使得所有的依赖关系都能够被满足。
步骤如下:
- 初始化入度表和邻接表:遍历图中的所有节点,记录每个节点的入度和出边节点。
- 构建入度为0的节点队列:将入度为0的节点加入队列。
- 遍历队列,删除该节点的出边,更新入度表:从队列中取出一个节点,遍历该节点的出边节点,将其入度减1,并更新入度表。
- 如果被删除节点的出边节点入度为0,加入队列:如果某个节点的入度减为0,则将其加入队列。
- 重复步骤3和4,直到队列为空。
- 判断是否有环,若有环则无法进行拓扑排序:如果图中存在入度不为0的节点,则说明图中存在环,无法进行拓扑排序。
- 输出拓扑排序结果:按照队列中节点的顺序,输出拓扑排序结果。
4. 该算法的手写实现总结和思维拓展
通过手写实现拓扑排序算法,可以更深入地理解该算法的原理和实现过程。在实现过程中,需要注意对入度表和邻接表的更新,以及对环的判断。思维拓展可以从以下几个方面进行:
- 如何优化拓扑排序算法的时间复杂度?
- 如何处理带权重的有向无环图的拓扑排序?
- 如何处理有环图的拓扑排序需求?
5. 该算法的完整代码
import java.util.*;public class TopologicalSort {public static List<Integer> topologicalSort(int numCourses, int[][] prerequisites) {// 初始化入度表和邻接表int[] inDegree = new int[numCourses];List<List<Integer>> adjacency = new ArrayList<>();for (int i = 0; i < numCourses; i++) {adjacency.add(new ArrayList<>());}for (int[] prerequisite : prerequisites) {inDegree[prerequisite[0]]++;adjacency.get(prerequisite[1]).add(prerequisite[0]);}// 构建入度为0的节点队列Queue<Integer> queue = new LinkedList<>();for (int i = 0; i < numCourses; i++) {if (inDegree[i] == 0) {queue.offer(i);}}// 遍历队列,删除该节点的出边,更新入度表List<Integer> result = new ArrayList<>();while (!queue.isEmpty()) {int curr = queue.poll();result.add(curr);for (int next : adjacency.get(curr)) {inDegree[next]--;if (inDegree[next] == 0) {queue.offer(next);}}}// 判断是否有环,若有环则无法进行拓扑排序if (result.size() != numCourses) {return new ArrayList<>();}return result;}
}
6. 该算法的应用前景调研
拓扑排序算法在任务调度、编译器优化、依赖关系分析等领域有着广泛的应用前景。随着大数据、人工智能等技术的发展,对于处理复杂依赖关系的需求越来越多,拓扑排序算法的应用前景也越来越广阔。
7. 该算法的三个拓展应用案例
拓展应用案例1: 课程安排
public class CourseSchedule {public boolean canFinish(int numCourses, int[][] prerequisites) {int[] inDegree = new int[numCourses];List<List<Integer>> adjacency = new ArrayList<>();for (int i = 0; i < numCourses; i++) {adjacency.add(new ArrayList<>());}for (int[] prerequisite : prerequisites) {inDegree[prerequisite[0]]++;adjacency.get(prerequisite[1]).add(prerequisite[0]);}Queue<Integer> queue = new LinkedList<>();for (int i = 0; i < numCourses; i++) {if (inDegree[i] == 0) {queue.offer(i);}}int count = 0;while (!queue.isEmpty()) {int curr = queue.poll();count++;for (int next : adjacency.get(curr)) {inDegree[next]--;if (inDegree[next] == 0) {queue.offer(next);}}}return count == numCourses;}
}
拓展应用案例2: 任务调度
public class TaskScheduler {public int leastInterval(char[] tasks, int n) {int[] count = new int[26];for (char task : tasks) {count[task - 'A']++;}PriorityQueue<Integer> pq = new PriorityQueue<>(26, Collections.reverseOrder());for (int c : count) {if (c > 0) {pq.offer(c);}}int intervals = 0;while (!pq.isEmpty()) {List<Integer> temp = new ArrayList<>();for (int i = 0; i <= n; i++) {if (!pq.isEmpty()){int curr = pq.poll();if (curr > 1) {temp.add(curr - 1);}intervals++;if (pq.isEmpty() && temp.size() == 0) {break;}}for (int i : temp) {pq.offer(i);}}return intervals;}}
}
拓展应用案例3: 编译器优化
public class CompilerOptimization {public List<String> optimizeCompiler(List<String> dependencies) {Map<String, Integer> inDegree = new HashMap<>();Map<String, List<String>> adjacency = new HashMap<>();for (String dependency : dependencies) {String[] parts = dependency.split("->");String from = parts[0];String to = parts[1];inDegree.put(from, inDegree.getOrDefault(from, 0));inDegree.put(to, inDegree.getOrDefault(to, 0) + 1);adjacency.putIfAbsent(from, new ArrayList<>());adjacency.get(from).add(to);}Queue<String> queue = new LinkedList<>();for (String node : inDegree.keySet()) {if (inDegree.get(node) == 0) {queue.offer(node);}}List<String> result = new ArrayList<>();while (!queue.isEmpty()) {String curr = queue.poll();result.add(curr);if (adjacency.containsKey(curr)) {for (String next : adjacency.get(curr)) {inDegree.put(next, inDegree.get(next) - 1);if (inDegree.get(next) == 0) {queue.offer(next);}}}}return result;}
}
案例总结
拓扑排序是一种针对有向无环图(DAG)的排序算法,它可以将图中的节点按照依赖关系进行排序。拓扑排序在许多领域中都有广泛的应用,下面是一些常见的应用总结:
-
任务调度:在任务调度中,有些任务可能存在依赖关系,即某些任务必须在其他任务执行完成后才能开始。通过拓扑排序,可以确定任务的执行顺序,保证任务按照依赖关系进行调度。
-
课程安排:在学校或大学中,课程之间通常存在依赖关系,即某些课程必须在其他课程之前完成。拓扑排序可以帮助学校进行课程安排,确保学生按照正确的顺序学习课程。
-
编译顺序:在编译过程中,源代码中的模块或函数可能会相互调用,存在依赖关系。拓扑排序可以确定编译的顺序,确保每个模块都在其依赖的模块之后编译。
-
依赖关系管理:在软件开发中,模块或组件之间常常存在依赖关系。通过拓扑排序,可以管理和解决模块之间的依赖关系,以确保软件的正确构建和部署。
-
项目管理:在项目管理中,任务的前后关系和依赖关系是重要的考虑因素。通过拓扑排序,可以确定任务的执行顺序,从而帮助项目团队有效地计划和管理项目进度。
总之,拓扑排序在任务调度、课程安排、编译顺序、依赖关系管理和项目管理等方面都有重要的应用。它能够解决依赖关系问题,确保任务按照正确的顺序执行,提高效率和准确性。
相关文章:

Java手写拓扑排序和拓扑排序应用拓展案例
Java手写拓扑排序和拓扑排序应用拓展案例 1. 算法思维导图 #mermaid-svg-o8KpEXzxukfDM8c9 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-o8KpEXzxukfDM8c9 .error-icon{fill:#552222;}#mermaid-svg-o8KpEXzxukfD…...

练习:使用servlet显示试卷页面
试卷页面代码 在浏览器输入如下地址: http://localhost/examPageServlet 效果如下:...
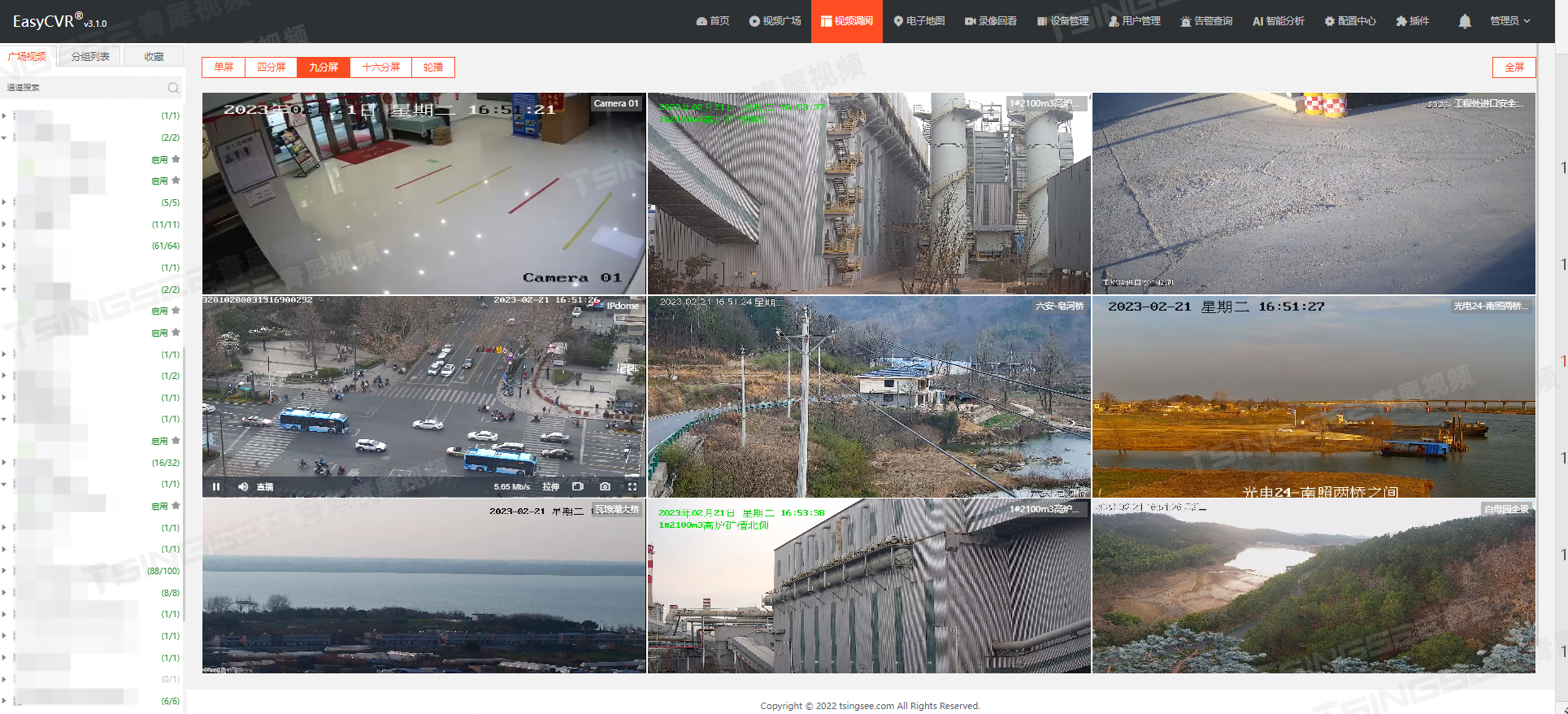
视频监控系统/视频云存储EasyCVR接入国标GB28181设备无法播放设备录像,是什么原因?
安防视频监控平台EasyCVR支持将部署在监控现场的前端设备进行统一集中接入,可兼容多协议、多类型设备,管理员可选择任意一路或多路视频实时观看,视频画面支持单画面、多画面显示,视频窗口数量有1、4、9、16个可选,还能…...
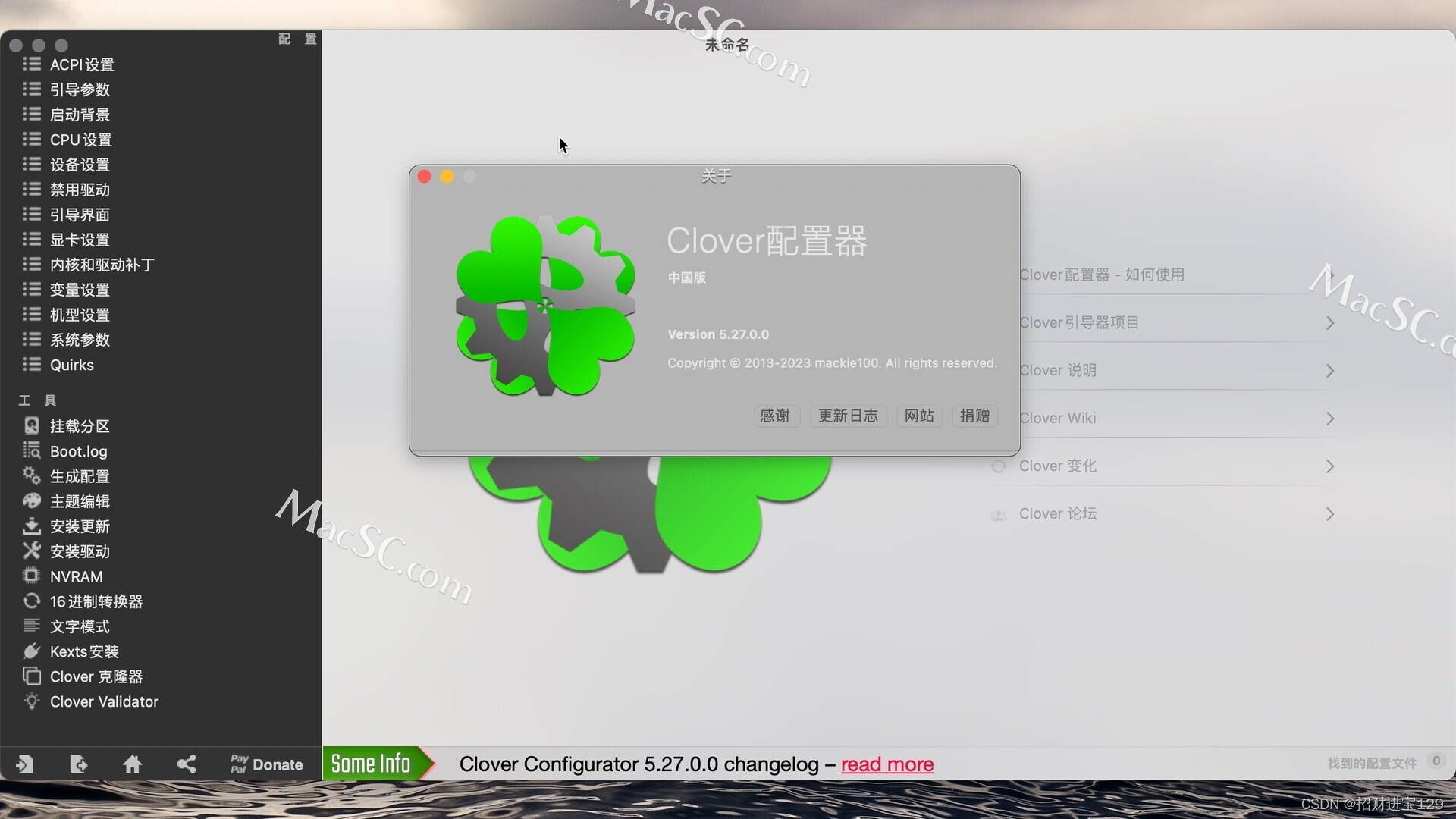
四叶草clover配置工具:Clover Configurator for Mac
Clover Configurator是一款Mac上的工具,用于配置和优化Clover引导加载器。Clover引导加载器是一种用于启动macOS的开源引导加载器。它允许用户在启动时选择操作系统和配置启动选项。 Clover Configurator提供了一个可视化的界面,让用户可以轻松地编辑和…...
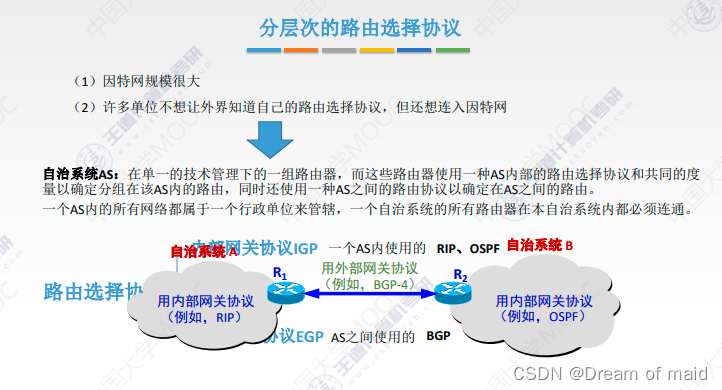
计算机网络第四章——网络层(中)
提示:待到山花烂漫时,她在丛中笑。 文章目录 需要加头加尾,其中头部最重要的就是加了IP地址和MAC地址(也就是逻辑地址和物理地址)集线器物理层设备,交换机是物理链路层的设备,如上图路由器左边就…...
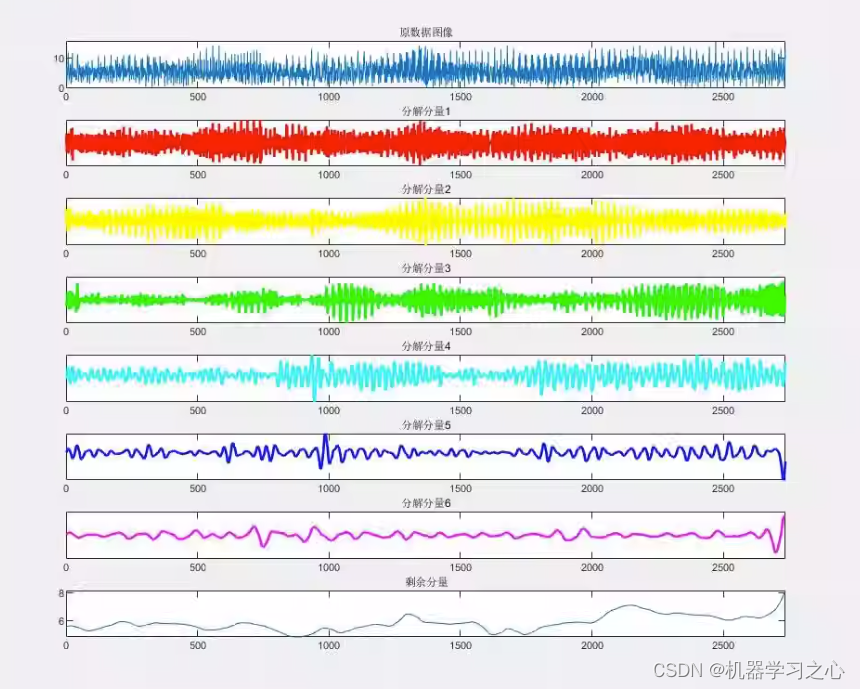
时序分解 | MATLAB实现基于小波分解信号分解分量可视化
时序分解 | MATLAB实现基于小波分解信号分解分量可视化 目录 时序分解 | MATLAB实现基于小波分解信号分解分量可视化效果一览基本介绍程序设计参考资料 效果一览 基本介绍 基于小波分解的分量可视化,MATLAB编程程序,用于将信号分解成不同尺度和频率的子信…...

VMware虚拟化环境搭建
虚拟化环境搭建 1. 什么是虚拟化环境?未来工作中在何处使用? 在网络安全中,虚拟化环境是一种技术,它将一个物理计算机系统划分成多个独立、可管理的虚拟环境。这种虚拟环境技术允许多个完全不同的操作系统、显示装置和软件在同一…...
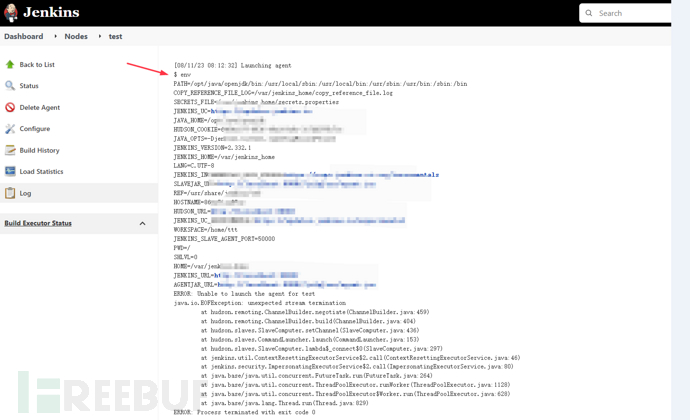
Jenkins :添加node权限获取凭据、执行命令
拥有Jenkins agent权限的账号可以对node节点进行操作,通过添加不同的node可以让流水线项目在不同的节点上运行,安装Jenkins的主机默认作为master节点。 1.Jenkins 添加node获取明文凭据 通过添加node节点,本地监听ssh认证,选则凭…...

如何实现不同MongoDB实例间的数据复制?
作为一种Schema Free文档数据库,MongoDB因其灵活的数据模型,支撑业务快速迭代研发,广受开发者欢迎并被广泛使用。在企业使用MongoDB承载应用的过程中,会因为业务上云/跨云/下云/跨机房迁移/跨地域迁移、或数据库版本升级、数据库整…...
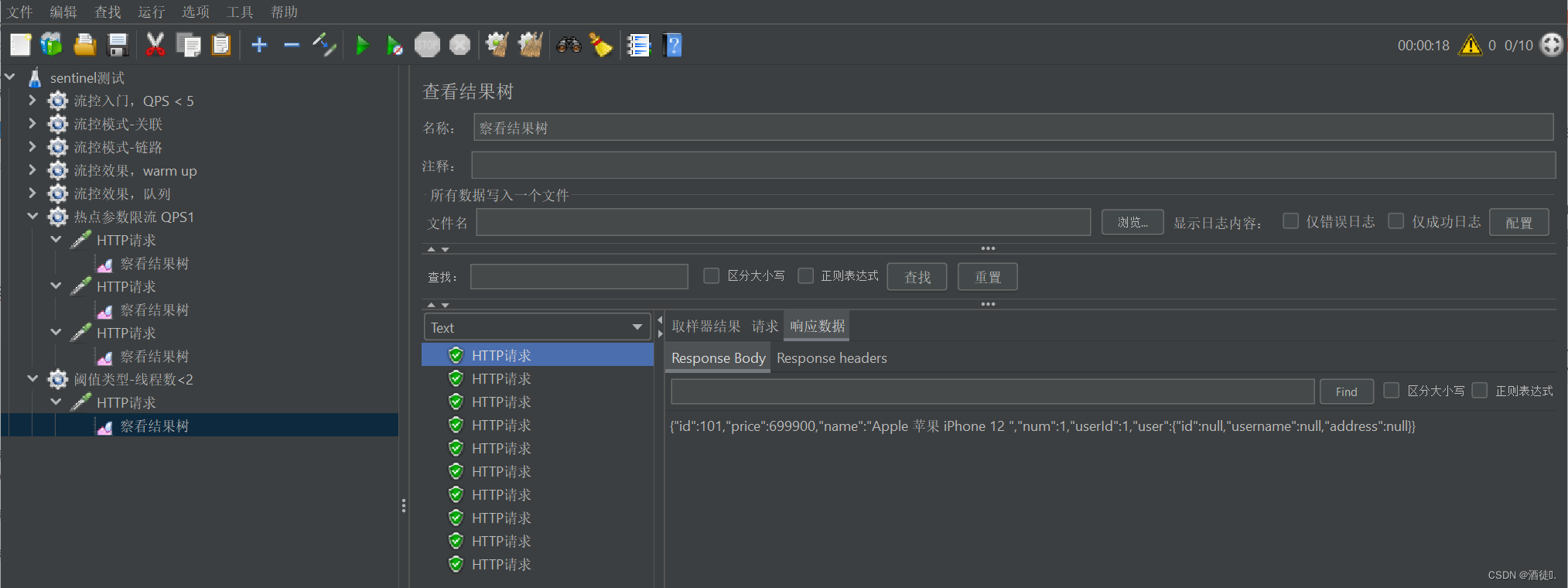
微服务保护-隔离
个人名片: 博主:酒徒ᝰ. 个人简介:沉醉在酒中,借着一股酒劲,去拼搏一个未来。 本篇励志:三人行,必有我师焉。 本项目基于B站黑马程序员Java《SpringCloud微服务技术栈》,SpringCloud…...

报错:appium AttributeError: ‘NoneType‘ object has no attribute ‘to_capabilities‘
报错如下 Traceback (most recent call last):File "C:\Users\wlb\Desktop\test\python\2.py", line 16, in <module>driver webdriver.Remote("http://127.0.0.1:4723/wd/hub", caps)File "D:\software\python3\lib\site-packages\appium\we…...
MFC - 一文带你从小白到项目应用(全套1)
文章篇幅可能会比较长,从入门到基本能上项目的全部内容。建议观看的过程中,用电脑跟着学习案例。 持续输出优质文章是作者的追求,因为热爱,所以热爱。 最近看动漫被一句鸡汤感动到了,也送给各位朋友: 只要有…...
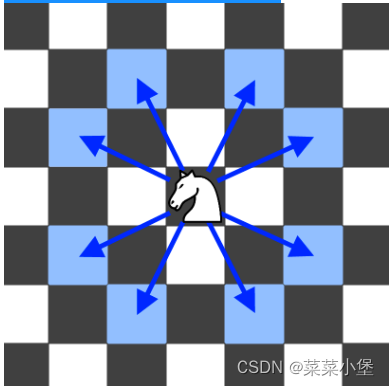
(2596. 检查骑士巡视方案leetcode,经典深搜)-------------------Java实现
(2596. 检查骑士巡视方案leetcode,经典深搜)-------------------Java实现 题目表述 骑士在一张 n x n 的棋盘上巡视。在 有效 的巡视方案中,骑士会从棋盘的 左上角 出发,并且访问棋盘上的每个格子 恰好一次 。 给你一个 n x n …...

Docker 部署 Bitwarden RS 服务
Bitwarden RS 服务是官方 Bitwarden server API 的 Rust 重构版。因为 Bitwarden RS 必须要通过 https 才能访问, 所以在开始下面的步骤之前, 建议先参考 《Ubuntu Nginx 配置 SSL 证书》 配置好域名和 https 访问。 部署 Bitwarden RS 拉取最新版本的 docker.io/vaultwarden…...

python与mongodb交互-->pymongo
from pymongo import MongoClient# 创建数据库连接对象 client=MongoClient(ip,27017)# 选择一个数据库 db=client[admin]db.authenticate(python,python)# 选择一个集合 col=client[pydata][test]col.insert({"class":"python"})col.find() for data in c…...
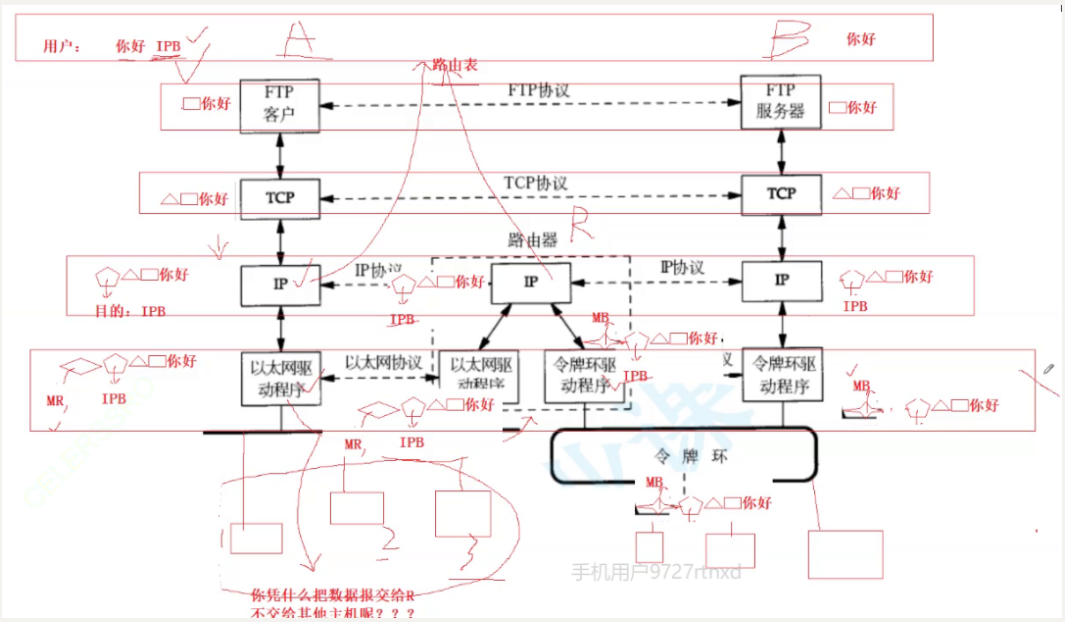
【网络】计算机网络基础
Linux网络 对网络的理解 在网络传输中存在的问题: 找到我们所需要传输的主机解决远距离数据传输丢失的问题怎么进行数据转发,路径选择的问题 有问题,就有解决方案; 我们把相同性质的问题放在一起,做出解决方案 解…...
输入输出函数:cin和cout(2)数学函数:sqrt、pow、sin、cos、tan等)
(1)输入输出函数:cin和cout(2)数学函数:sqrt、pow、sin、cos、tan等
输入输出函数:cin 和 cout 在C编程语言中,为了与用户进行交互和显示程序的结果,我们使用了两个非常重要的函数:cin 和 cout。这两个函数分别用于输入和输出。 cin是C中的标准输入流对象,它用于从键盘接收用户的输入。…...

ArmSom-W3开发板之PCIE的开发指南(一)
1. 简介 RK3588从入门到精通本⽂介绍RK平台配置pcie的方法开发板:ArmSoM-W3 2、PCIE接口概述 PCIe(Peripheral Component Interconnect Express)是一种用于连接计算机内部组件的高速接口标准。以下是关于PCIe接口的简要介绍: …...

Android 13.0 framework修改AlertDialog对话框的button样式
1.概述 在13.0系统产品开发中 在AlertDialog 系统对话框原生的确定和取消 两个button 按钮中,由于产品觉得字体默认颜色的不太好看,由于产品的需求修改button字体的颜色,所以需要找到AlertDialog的字体样式然后修改就可以了 2.framework修改AlertDialog 对话框的button样式…...
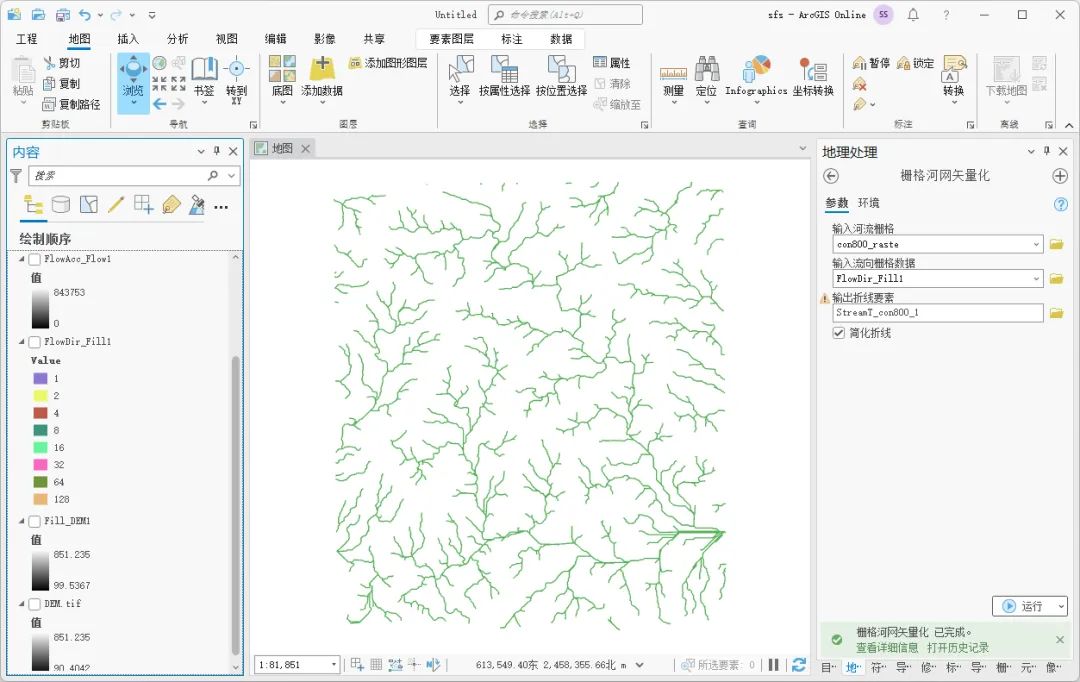
如何使用ArcGIS Pro提取河网水系
DEM数据除了可以看三维地图和生成等高线之外,还可以用于水文分析,这里给大家介绍一下如何使用ArcGIS Pro通过水文分析提取河网水系,希望能对你有所帮助。 数据来源 本教程所使用的数据是从水经微图中下载的DEM数据,除了DEM数据&a…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...
